双层转角石墨烯结构和弹性性质的第一性原理
2020-11-16陈鸿杰周晓林
陈鸿杰, 王 朝, 程 才, 刘 科,2, 周晓林*
(1.四川师范大学物理与电子工程学院,四川成都610101;2.电子科技大学电子薄膜与集成器件国家重点实验室,四川成都610065)
二维材料以特定顺序组合形成多层范德华异质结,从而展现出了许多新奇的物理特性,引起了人们的广泛关注[1].这些异质结在纳米电子学、纳米光学和催化等领域有着非常重要的应用[2-4].双层石墨烯是最简单的多层结构,单层石墨烯中碳原子之间强共价键维持了二维结构的稳定性[5],而层间相对较弱的范德华力又使单层结构结合在一起.众所周知,单层石墨烯在各个方面表现出优异的特性.例如:室温下超高的电荷载流子迁移率(1 500 cm2/(V·s))[6]、较高的热导系数(2 500 ~3 000 W/mK)[7].此外,在理论和实验的研究中还发现双层石墨烯中存在着新的范霍夫奇点[8]、费米速度重整化[9]、新奇的手性隧穿以及非常规量子霍尔效应[10]等.以上的研究表明,这些性质和双层石墨烯之间的堆叠方式有关,常见的有AA和AB 堆叠[11].在上述2种堆叠方式的基础上,可以任意旋转其中一层石墨烯,最终形成不同的层间转角,如图1所示.

图1 双层转角石墨烯的结构Fig. 1 Structure diagram of the twisted graphene bilayer
在旋转的双层结构中,上下2 个蜂窝状晶格的叠加会产生具有较大周期的莫尔纹超晶格,利用STM图像可以清楚地观察到莫尔纹模式的超晶格形成[12-14].作为一种新兴的超结构,莫尔超晶格表现出原固有晶格不具备的特性.2018 年,Cao等在双层石墨烯转角θ≈1.08°时观察到了非传统的超导现象[15]和一个毫电子伏特宽度的平带出现[16].这一现象的发现,再次引起了人们对其相关性质研究的极大兴趣.然而到目前为止,对双层转角石墨烯的弹性性质研究相对较少.
本文系统地分析了不同转角双层石墨烯的结构和弹性性质.首先,用基于密度泛函方法的量子力学软件VASP(Vienna Ab -inito Simulation Package)对AB堆叠的双层石墨烯进行结构优化.由于双层石墨烯结构中存在弱的范德华力,因此在结构优化过程中考虑了4 种泛函对范德华相互作用的修正,并确定最适合双层石墨烯结构的泛函.其次,在选用的泛函下对不同转角的双层结构进行了晶格优化.最后,利用优化的晶格结构,系统分析了不同双层转角石墨烯的弹性性质.
1 模型建立与计算方法
1.1 模型建立双层转角石墨烯由两层石墨烯叠加而成,如图1(a)所示.单层石墨烯结构的晶格基矢分别表示为:
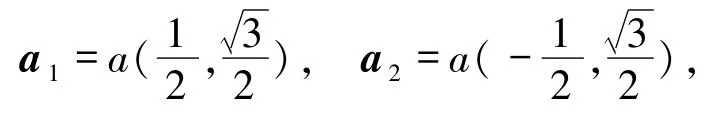
其中a是晶格常数.在满足层间晶格匹配的条件下,双层结构的超晶格基矢分别表示为

其中,m、n为整数,角标表示层数,则相对旋转角度定义为
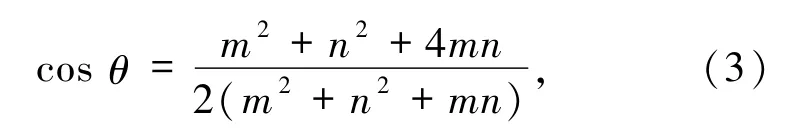
超晶格的晶格常数表示为
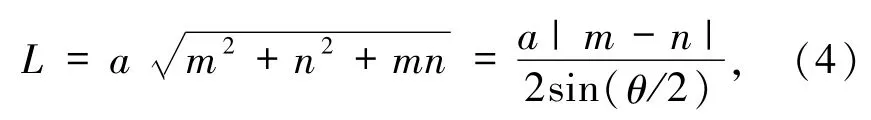
每个超晶格的碳原子数
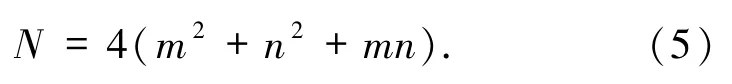
选取不同的 m、n 值,根据(3)~(5)式可以得出不同旋转角下的晶格常数和原子数目.若两层之间的旋转角度越小,体系的超单元就越大,即晶胞中包含的原子数目就越多.考虑到从头算对大体系计算处理时长以及超大计算资源的需求,故在不影响研究的前提下,选择了8 个原子数相对较少的旋转角.表1 列出了8 个转角下的晶格常数、原子数目、对应的 m、n以及布里渊区中 K点的取值.当θ =0°时,表示上下2层石墨烯完美重叠,即AA堆叠,如图1(b);θ =60°时,上下2 层重叠的方式类似石墨的堆叠方式,即 AB 堆叠,如图1(c).
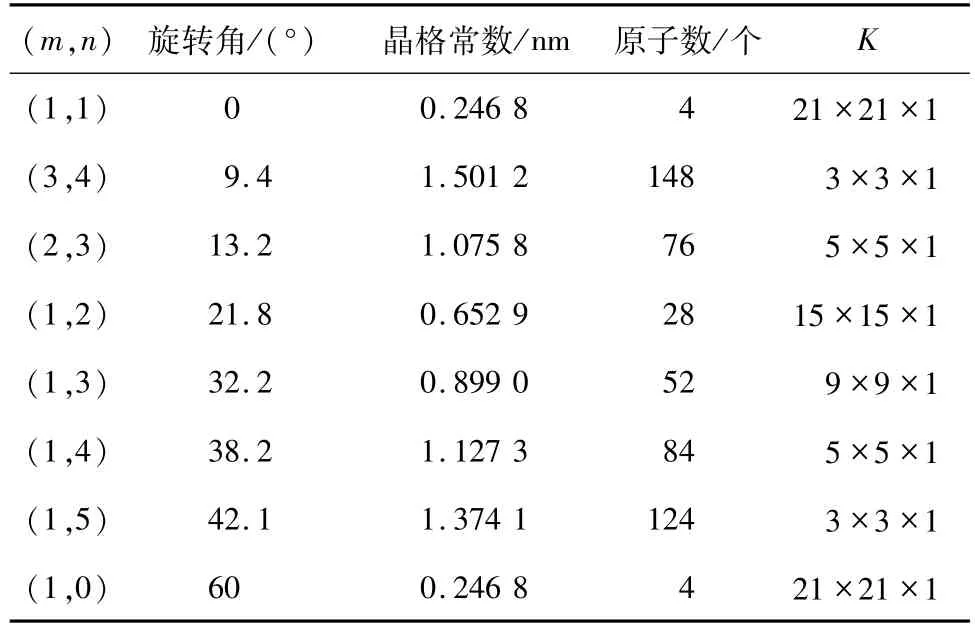
表1 双层石墨烯一些转角下的晶格常数、原子数、(m,n)以及布里渊区中K点值Tab. 1 The lattice constant,number atoms,(m,n)and the K value in the Brillouin zone of some twisted graphene bilayer
1.2 计算方法基于密度泛函理论的第一性原理,结合采用平面波基组实现投影缀加波(PAW)方法[17]的VASP软件包.在计算中选择广义梯度近似(GGA)泛函下的Perdew-Burke-Ernzerhof(PBE)来描写电子的交换关联能作用[18].在PAW 赝势中碳原子的价电子为(2s2,2p2),这里采用 500 eV 作为平面波截断能.考虑了4 种不同的泛函对范德华相互作用的修正:DFT - D2、optB88 - vdW、optPBE-vdW和vdW-DF2[19-22].在计算过程中原子平均受力小于0.1 eV/nm,电子自洽计算收敛精度小于10-5eV.为了消除与周期边界条件的相互作用,取真空层距为1.5 nm.
2 结果与讨论
2.1 范德华相互作用对结构的影响首先考虑了AB堆叠在不同泛函下对其结构的影响.表2 列出了PBE泛函和4 种修正泛函下AB堆叠时的平衡碳碳键长、层间距离和层间结合能.结果表明,修正泛函对层间距和层间结合能均有良好的修正,而对层内碳碳键的长度几乎没有影响.比较不同泛函的修正结果,发现在optB88 -vdW泛函修正下的层间距为0.334 nm,结合能为-66 meV/atom,这与之前的理论计算和实验结果均十分吻合[23-24].因此,在本文后续的计算中都采用了该修正泛函.
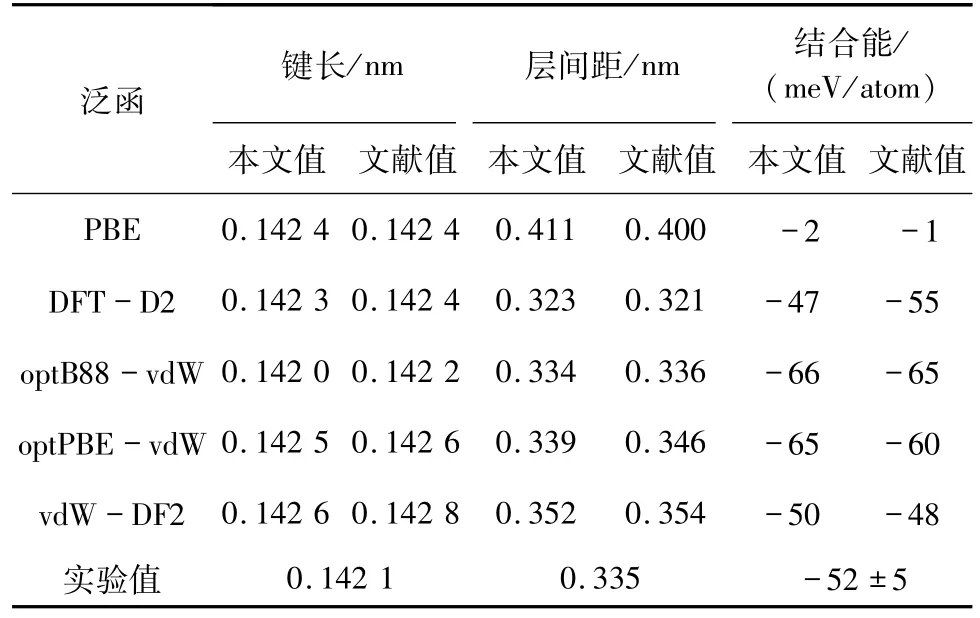
表2 不同泛函下AB堆叠的键长、层间距和结合能比较Tab. 2 Compared bond length,layer distance and binding energy of AB stacking under different functionals
表3 列出了各扭转角下层间结合能和层间距离.可以看出,当 θ =0°时,层间距和结合能分别为0.351 9 nm 和 -52.0 meV/atom,当 θ =60°时,层间距和结合能分别为0.334 2 nm 和-66 meV/atom.总结不同转角下的层间结合能和距离变化规律,发现层间结合能和距离随旋转的角度增加而减小.层间平衡距离越远,层间的结合能越弱,即范德华相互作用也更小,这类似于分子或固体的一般化学趋势.
2.2 弹性性质对双层转角石墨烯结构弹性性质的研究,不仅更深刻地理解层间范德华相互作用,而且对实际应用也提供了重要的参数依据.对于双层转角石墨烯二维弹性常数记为C11、C22、C12、C66(采用标准的 Voigt 符号:1 -xx、2 -yy、6 -xy).在面内应力条件下,根据胡克定律给出弹性常数与模量之间的关系[25]

表3 不同转角下的层间距和结合能Tab. 3 Layer distance and binding energy at different twisted angles

这里 Cij(i,j =1,2,6)是平面内的弹性刚度系数,且
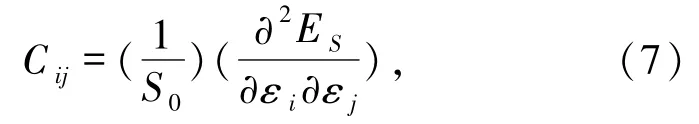
S0是结构没有施加应变时的面积,ES是系统的应变能(应变结构的能量减去初始结构的能量).在极小的应变下,原子平均应变能表示为
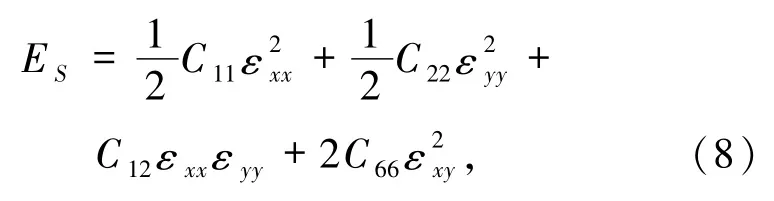
这里的应变定义为
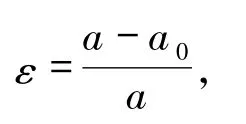
a和a0分别代表应力状态和平衡状态的晶格常数.若对晶格施加沿x方向的单轴应变,则对应的原子平均应变能为
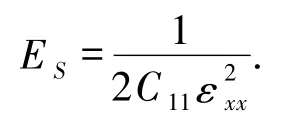
通过对应变和原子平均应变能的二次拟合,得到的二次项系数为C11.同理,可依次计算其他弹性系数.如图2 所示,圆圈、五角和三角分别表示对不同转角下的结构施加了-2% ~2%的单轴和双轴的应变(间隔为0.5%),对应曲线表示对应变和原子平均应变能的二次拟合.可以看出,在施加应变±2%的范围内,不同转角中没有出现明显的能量畸变点,并且应变能的大小是和结构中原子数呈正相关的.
双层转角石墨烯属于六角晶系,由六角结构的对称性得:
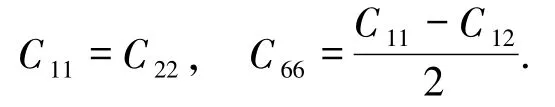
这些弹性常数与层模量(γ)、杨氏模量(Y)、剪切模量(G)和泊松比(ν)的关系分别表示为:
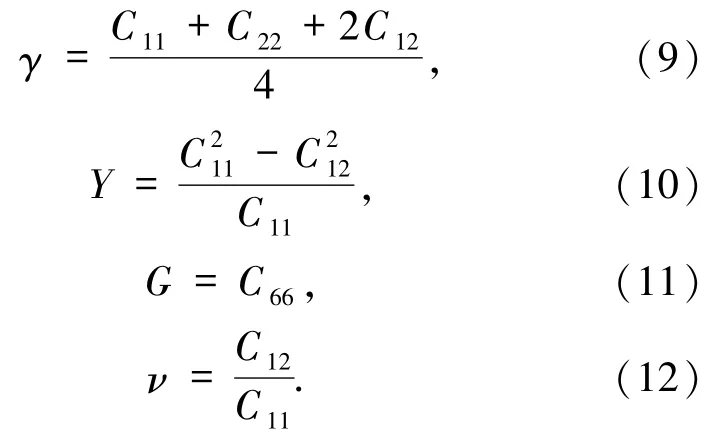
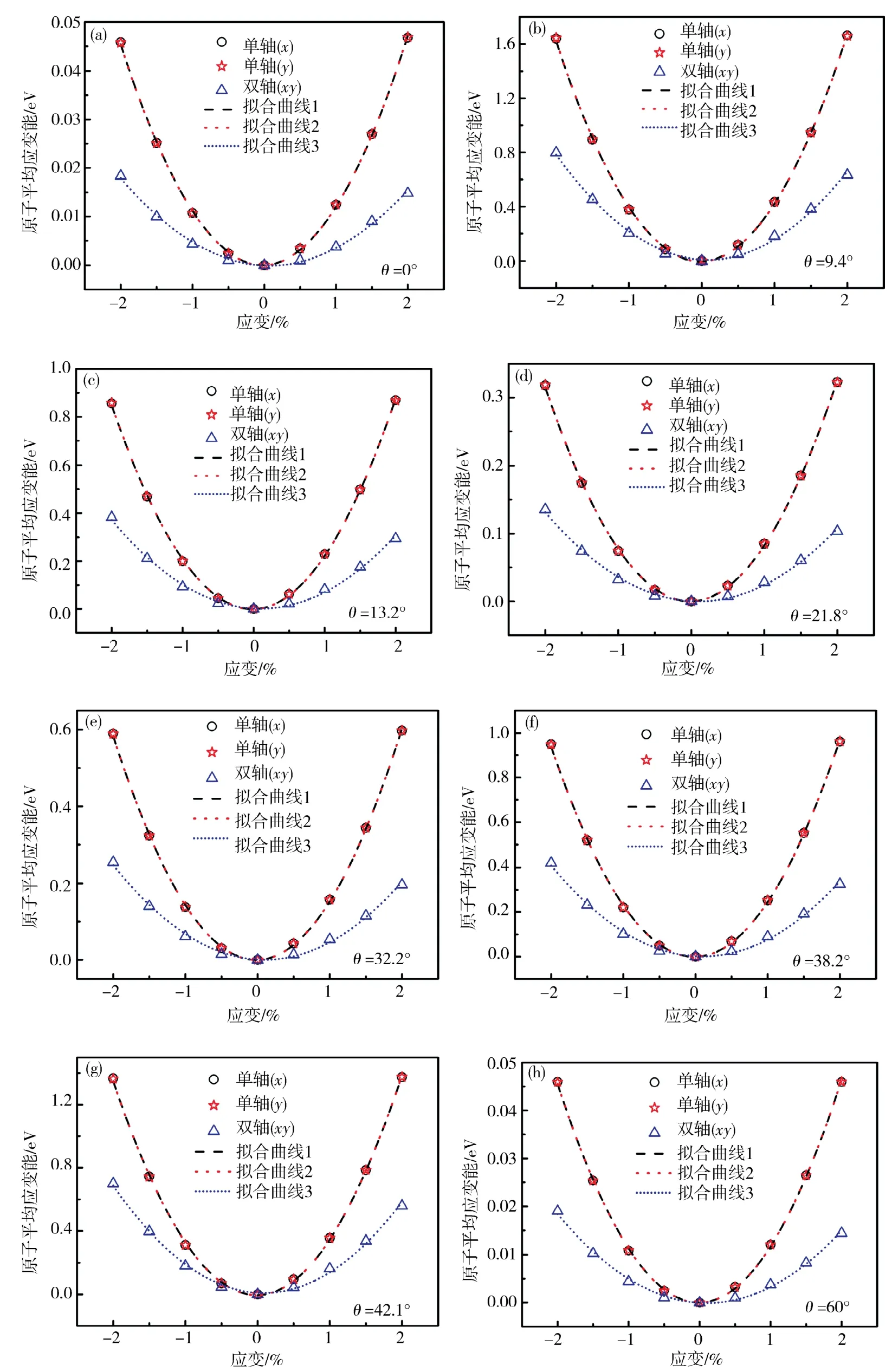
图2 不同转角下单、双轴应变和原子平均应变能Fig. 2 The uniaxial,biaxial strain and atomic average strain energy at different twisted angles

表4 双层转角石墨烯和单层石墨烯的弹性常数、模量和泊松比Tab. 4 The elastic constants,modulus and poisson’s ratio of the twisted bilayer and monolayer graphene
根据(9)~(12)式,计算了双层转角石墨烯和单层石墨烯的弹性常数、各个模量和泊松比,如表4所示.根据玻恩理论的力学稳定性条件,对于二维六角结构 C11>0、C66>0 和 C11> |C12|可知,在不同旋转角下,研究的结构是力学性稳定的.在转角θ =0°时,双层结构的弹性常数和模量约等于单层石墨烯的2 倍,而泊松比与单层结构的相同.说明在转角θ =0°的情况下,双层结构性质与单层结构相似.在图3 中分别展示了弹性常数和模量随转角的变化.从图3(a)观察到,随着转角的增加,C11先减小再增加,然后再减小再增加,并且在其他转角下C11的值均小于转角在0°和60°的情况,而C12呈现相反的规律.从图3(b)观察到,不同转角下层模量几乎保持不变,剪切模量和杨氏模量表现出与C11类似的变化规律.剪切和杨氏模量表征材料的刚性,在其他转角下剪切和杨氏模量的值均比在0°和60°情况下的小,即层间更容易发生相对滑移.
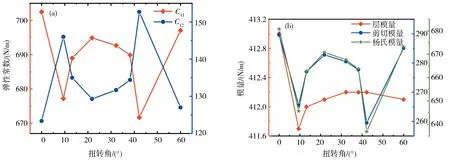
图3 不同转角下的弹性常数和模量Fig. 3 The elastic constants and modulus at different twisted angles
3 结论
本文基于密度泛函理论的第一性原理,系统地分析了双层转角石墨烯的晶格结构和弹性性质.在结构性质中,表明范德华相互作用在双层石墨烯中扮演了重要的角色,optB88 -vdW修正泛函能够很好地描述其相互作用,同时层间距是依赖转角的,当转角 θ = 0°(60°)时层间距最大(小),其他转角下层间距介于 θ =0°和 θ =60°之间.在弹性性质中,计算出了不同双层转角石墨烯的弹性常数和模量.结果表明,其层模量不依赖转角,在θ =0°的剪切模量和杨氏模量值最大,分别为289.6 和680.8 N/m.以转角θ =21.8°为分界点,杨氏模量和剪切模量随转角增大,表现出先减后增的变化规律.对双层转角石墨烯的结构和弹性性质的分析结果,为双层转角石墨烯材料在实际应用中提供了理论参考.
