全并联AT牵引网行波故障测距研究

贺凤珂, 陈保平，安晓静，王艺霏

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

0 引言

2016年7月，国家发改委印发了经国务院批准的新一版《中长期铁路网规划》，该规划方案指出，我国将建成“八纵八横”高速铁路网。规划目标：到2020年，铁路网规模达到15万km，其中高速铁路3万km，覆盖80%以上的大城市；到2025年，铁路网规模达到17.5万km左右，其中高速铁路3.8万km左右；到2030年全国铁路基本实现内外互联互通、区际多路畅通、省会高铁连通、地市快速通达、县域基本覆盖[1]。这为实现经济社会持续健康发展、实现“两个一百年”奋斗目标提供强有力的支撑。电气化铁路牵引网都暴露在环境恶劣的户外，且承受受电弓的高速机械震动摩擦，致使其故障频发[2]。而电气化铁路牵引网则作为电能传输的唯一导体介质，一旦线路上发生故障，就会影响线路的正常运行，需快速准确找出故障位置，这对高速电气化铁路运输具有很重要的现实意义。

目前我国电气化铁路牵引网按供电方式不同可分为直接供电方式、BT(吸流变压器)供电方式、AT(自耦变压器)供电方式以及CC(同轴电缆)供电方式[3]。在高速铁路牵引供电系统中主要采用AT供电方式，其根据线路连接结构可分为单线AT供电方式、复线AT供电方式以及全并联AT供电方式。其中，全并联AT供电方式的供电原理与复线AT供电方式基本相同，不同的是复线AT供电方式只是上下行末端线路采用并联供电，而全并联AT供电方式在每一个AT所和分区所处上下行线路都进行横向并联联接[4]，这样使得牵引网单位长度的阻抗减小，降低了电压损耗，从而增强牵引网系统的供电能力，改善电能质量，保证机车的安全、可靠、高速运行，在高速电气化铁路上有着广泛的应用。但因其线路结构复杂，一旦线路上发生故障情况，很难准确确定故障位置，这给牵引供电系统恢复供电、保障运行安全带来困难。文献[5]～文献[7]中所研究的线路只是复线AT供电方式，未对全并联AT供电方式的测距情况进行研究。本文则根据全并联AT供电系统线路特性搭建其仿真模型，研究线路故障时产生的信号特征及测距原理，可以快速准确测量出故障位置。

1 D型行波故障测距原理

行波具有传播速度稳定、测距精度高、不受线路结构及故障类型等因素影响的特点，被广泛应用于牵引网线路故障测距研究中。行波法是基于暂态行波的故障测距法，依据行波信号的测取方式可分为单端法和双端法。从理论分析上讲，单端法和双端法均可对牵引网进行故障测距。但是，牵引网线路本身结构以及设备非常复杂，严重影响行波的传播。另外，牵引网的线路分支较多，使行波发生复杂的反射和折射，不易识别，因此不宜采用单端行波法。相较而言，双端法中的D型行波法只需检测出初始行波到达两端的时间，无需考虑后续的反射波和折射波的影响，故采用D型双端行波故障测距法进行故障定位。

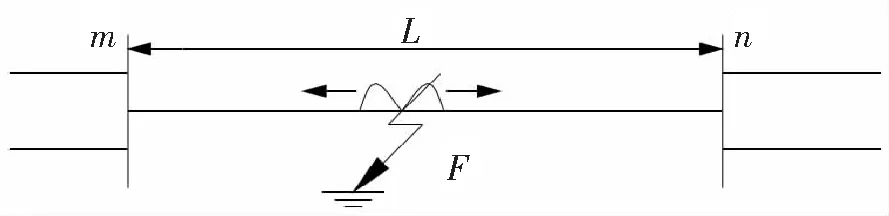
图1 D型行波测距原理示意图

D型行波测距法通过线路两端检测到的故障初始行波分别到达的时间之差，求得故障点距两端的距离。如图1所示。

设线路总长度为L，故障点距首端m和终端n的距离分别为DmF和DnF，而故障行波的初始波头以传播速度v分别向m端和n端传播，到达的时间分别为Tm和Tn，且有以下关系

(1)

整理可得

(2)

D型行波法是根据故障初始行波到达两端的时间来实现故障测距的，因此需要配备时间同步装置，把两端的时间统一到同一个基准下。文献[8]和文献[9]利用GPS卫星时钟同步技术进行时间同步，误差平均不超过1 ，测距绝对误差在200～300 m，这对现场寻找故障点还是有一定的困难。而选用北斗卫星导航系统，它具有单向和双向2种授时功能，根据不同的精度要求，利用授时终端，完成与北斗导航系统之间的时间与频率同步，可提供数十纳秒级的时间同步精度，测距绝对误差在30 m之内，完全满足牵引网故障测距要求。

2 全并联AT牵引供电系统及其仿真模型

2.1 全并联AT牵引供电系统

图2 全并联AT供电示意图

我国电气化铁道牵引供电系统采用工频单相27.5 kV交流供电方式，牵引供电系统主要有牵引变电所和牵引网两部分组成，牵引变电所使用一主一备2台牵引变压器，连接两路电源，将110 kV或220 kV电压降压为1×27.5 kV或2×27.5 kV，供给牵引网。全并联AT供电方式牵引网的线路主要包括承力索(C)、接触线(T)、正馈线(F)、钢轨(R)、保护线(PW)、贯通地线(GW)以及横联线(CPW)，其电气结构如图2所示。

2.2 仿真模型参数

利用ATP-EMTP暂态仿真软件建立全并联AT牵引网供电系统的线路仿真模型。取全并联AT牵引网模型的供电臂长度为20 km，将承力索、接触线、正馈线和保护线分别作为一相导线，2根钢轨等效为一相的两分裂导线，其中承力索每隔200 m与接触线电联接，保护线每隔1 km与上下行钢轨完全横向联接，建立J.Marti线路模型。另外，贯通地线GW埋于地下，与其他架空导线间的互阻抗可忽略不计，只考虑其自阻抗[10]，值为0.305+j0.759 ，且每隔1 km与上下行钢轨横向连接。导线主要参数与AT接触网导线空间分布图分别如表1和图3所示。

表1 导线主要参数

图3 AT接触网导线空间分布图(单位：m)

2.3 仿真模型

以线路空载情况下的上行线路8 km处发生T-R故障的仿真模型为例，线路模型选用ATP-EMTP软件中的J.Marti线路模型，它是与频率相关的线路模型，使用的是固定频率的相模变换矩阵，在线路两端设有电压、电流探测器，所建立的模型如图4所示。

图4 全并联AT接触网仿真模型

(1)AT所模块用一单相可饱和变压器表示，其变比为1∶1，原副边的电压有效值为27.5 kV，具体接线如图5所示。

图5 AT所接线

(2)故障模块用一时间可控开关与一电阻串联，串联电阻即为接地电阻，具体接线如图6所示。

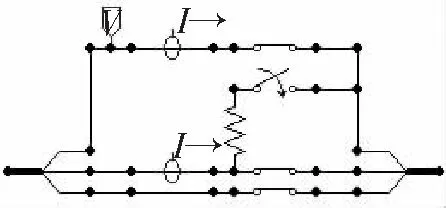
图6 故障模块接线

3 基于仿真平台行波测距

3.1 接触网线路相模变换及波速度

假设多相无损耗导线单位长度的电感和电容分别用矩阵[L]、[C]表示，则输电线路上的电流列向量I与导线对地电压列向量U与距离x和时间t有以下关系方程

(3)

对式(3)变换可得

(4)

设Q，S为多相输电线路电流列向量I和电压列向量U的模转换矩阵，因牵引网中LC≠CL，这种情况下，必须保证S=Q-T，才能消除多相导线间的电磁耦合。即有

S-1LCS=QTLCQ-T=(Q-1CLQ)T=A

(5)

则单位长度下的电感、电容的模量值为

(6)

各个模量分量具有对应的各自线路上的波速度，即为

(7)

由Carson理论和复数深度理论计算可以得到接触网线路电感、电容矩阵[L]、[C]，因接触线和承力索相同长度的压降相等，则可将两者合并，同理，将钢轨与保护线及贯通地线合并，即有

(8)

(9)

经相模变换可以得到模量分量的波传播速度,见表2。

表2 各模量波速度

其中，vm1为地模波速，vm2、vm3为2个线模波速，线路的不平衡性导致了线模波速的不一致，vm2为行波经接触线-正馈线回路的传播速度，vm3为行波经接触线-钢轨回路的传播速度，在利用行波波速确定故障位置时取线模vm3波速更为精确。

3.2 行波波头提取

设置仿真时间为60 ms，在20 ms时,上行线供电臂距m端8 km处发生接触网T-R故障，设定故障行波采样率为10 MHz。由仿真得到线路两端探测点测得的电压行波及波形局部放大如图7和图8所示。

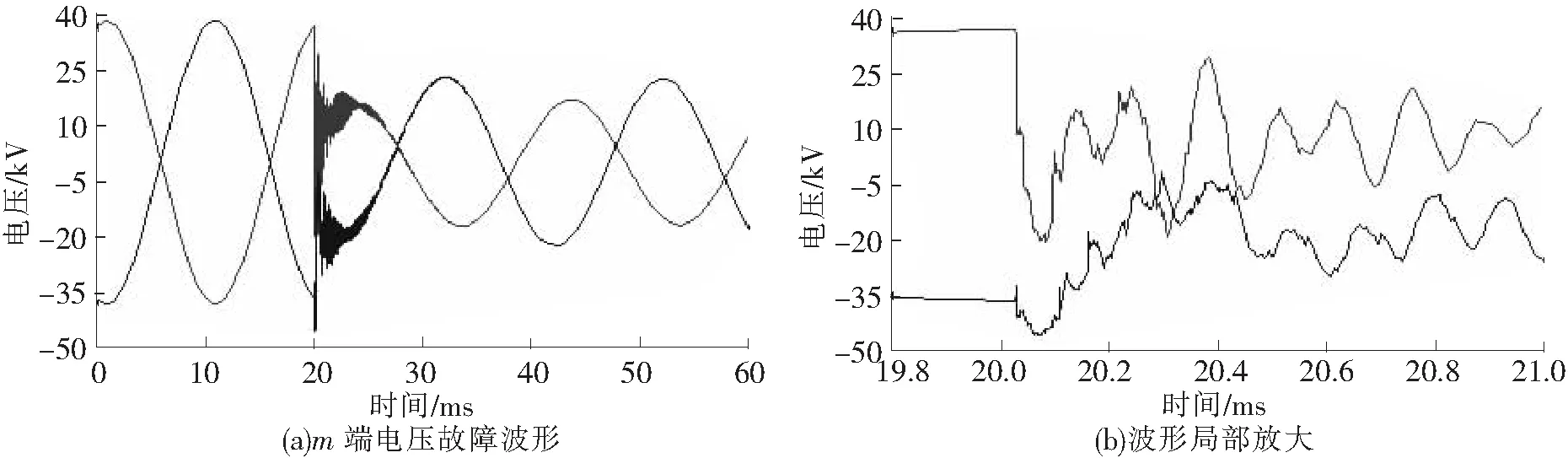
图7 m端电压行波

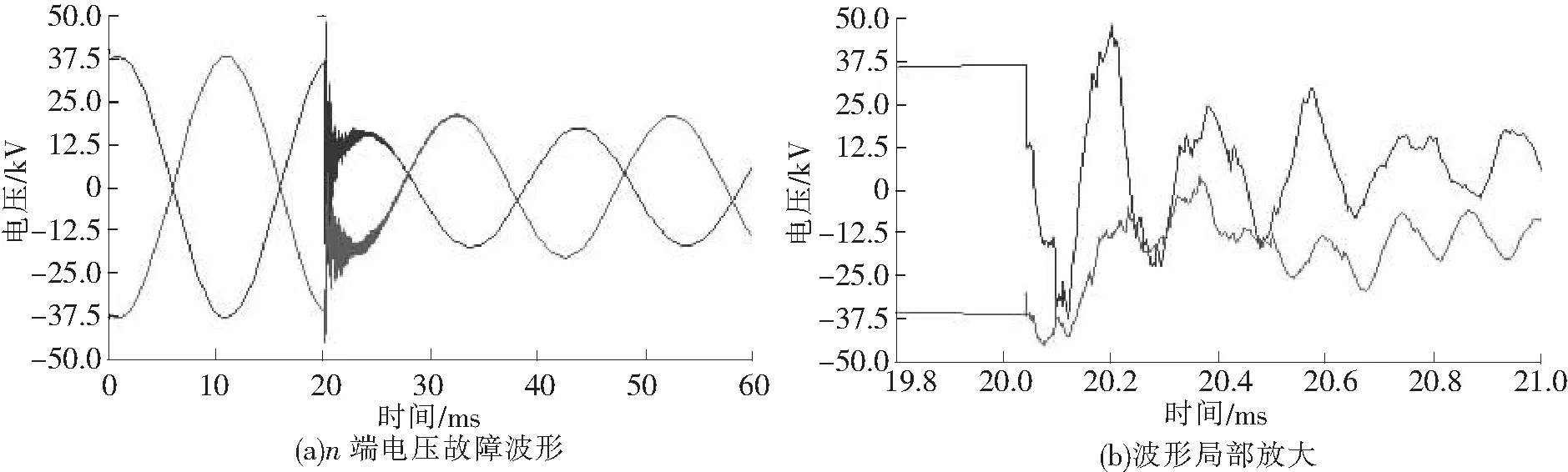
图8 n端电压行波

小波变换具有信号奇异性检测性质和变焦性质，对信号的奇异性和突变部分非常敏感，利用小波变换模极大值理论，可以识别出暂态行波信号的波头,并检测出波头相对应的精确时刻。将ATP-EMTP软件仿真得到的电压波形转换成Matlab可识别的*.mat数据流文件，利用Matlab编写db3小波变换的模极大值程序,对两端电压行波进行模极大值定位，效果如图9和图10所示。

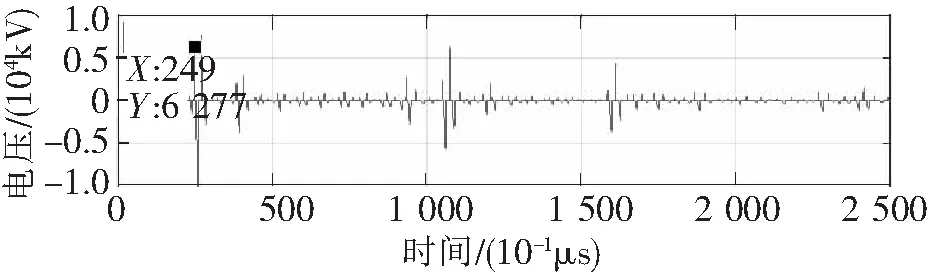
图9 m端小波变换的模极大值

图10 n端小波变换的模极大值

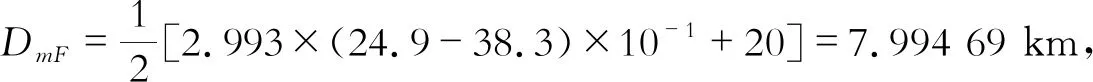
4 结论

利用ATP-EMTP软件中的J.Marti线路模型，将牵引网主要线路的参数与实际分布情况具体地仿真实现，得到了真实、可信的暂态行波。在牵引网中行波故障定位的最主要问题是波速的确定和行波波头的提取。对牵引网中的线路进行相模变换得到行波的地模、线模分量以及各分量的传播速度，对线模分量进行小波变换，并利用模极大值定位出行波波头位置，有效地解决了波速和波头提取的问题。进而通过D型行波故障测距原理求得故障距离，其结果与实际数据比较误差小于10 m，另有北斗卫星导航系统的时钟同步采样产生的绝对误差，则总体误差在40 m之内，满足故障测距要求。