交通荷载诱发振动传播规律和减振控制

袁金秀，叶 茂，崔海龙，孙永杰，王 悦，刘炳华，任 珉

(1. 河北交通职业技术学院 土木工程系，河北 石家庄 050091；2. 广州大学-淡江大学 工程结构灾害与控制联合研究中心，广东 广州 510006；3.河北建设集团股份有限公司，河北 保定 071000)

0 引言

为能够更好地满足城市居民的出行需求以及解决交通堵塞等城市发展问题，在国内外的大型城市，地铁、城轨等具有大运载量的城市轨道交通系统得到了迅猛发展。但是，由于城市轨道交通大多在城市内部穿越城市中心区，人群密集，在给人们出行游玩带来便利的同时，在运营过程中产生的振动和噪声也不容忽视。

针对振动和噪声这方面的问题，胥燕君等[1]对现代有轨电车轨道结构的选型、材料、路权使用等进行了系统介绍，系统归纳了不同有轨电车结构减振降噪措施的特点；刘婷林[2]基于国外嵌入式广泛使用的Corkelast弹性复合材料成本过高不利于投资，研究将废弃的橡胶高分子材料二次回收处理并应用到有轨电车轨道中；何远鹏等[3]利用有限元法和边界元法分别建立嵌入式轨道的振动计算模型和噪声计算模型；Lakušic et al[4]研究有轨电车经过城市内部时诱发的振动问题；Daniels[5]在研究嵌入式轨道设计时提到Edilon型钢轨埋入式无砟轨道，槽型轨周围填充Corkelast弹性复合材料，具有显著的减振降噪性能。

以上分析表明，关于轨道交通引起环境振动的研究，国内学者主要集中在针对地铁、轻轨和高速铁路，对于轻轨电车轨道减振降噪的研究起步较晚且内容较少。为此，本文将考虑车辆、轨道、道床以及土的性质等因素，利用ANSYS有限元软件，建立三维模型模拟轨道交通振动在场地土中传播，结合实测数据[6]和模拟数据分析不同钢轨弹性包覆材料的减振效果。

某轻轨电车试验段地面线路在钢轨两侧采用包裹高分子橡胶材料的措施，以实现减小环境振动的目的，钢轨弹性包覆材料造价不菲，因此全面综合性地分析该材料的减振性能显得尤为必要。按照包覆材料的截面形状分为双块式、套靴式和嵌条式，一共建立4种工况模型进行有限元分析,如图1所示。

图1 各工况模型局部放大示意图

1 轻轨电车移动荷载模拟

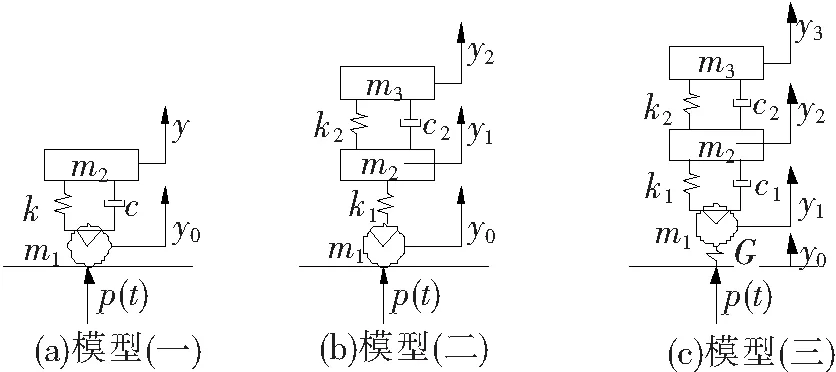
图2 车辆振动简化模型

分别采用实测分析法和经验分析法来模拟轻轨电车动荷载，对比2种方法的区别与相同点并为下文ANSYS模拟荷载输入奠定基础，将轻轨电车车辆简化为模型(一)[7]。主要考虑列车的竖向振动，忽略列车侧滚和横向振动，不考虑轮轨非线性接触，认为车轮与钢轨始终结合，如图2所示。

1.1 实测分析法

在现场测试所得的振动加速度数据曲线波形是明确的，但其表达式却是未知的，荷载数定法也即用公式来表达现场测得的振动加速度。研究表明，钢轨的振动加速度曲线可以分解成一系列不同频率的正弦波和余弦波之和，用傅里叶级数表示如下

(1)

式中，An定义为

(2)

式中，T为记录时间或者截断时间；N为采集数据的点数；基频ω=2π/T=2π/NΔt，Δt为采样时间间隔。将加速度曲线离散化为N个点

(3)

式中，离散化处理后An和Bn的定义如下

(4)

(5)

式中，Xk=X(tk)，即时间tk对应的加速度离散值。

经研究表明，加速度曲线离散采样经过快速傅里叶变换(FFT)后可以求得An和Bn，从而证明了式(3)是数定的，可以用来表达钢轨振动加速度曲线。

根据模型(一)可列出竖向振动动力平衡微分方程

(6)

该方程的求解过程不再赘叙，详解可查阅文献[8]，由达朗贝尔原理可得轮轨间相互作用力

(7)

则由P(t)经钢轨传至道床沿轨道均匀分布的线荷载

(8)

式中，n为每节车厢转向架数；L为每节车厢长度，以向下为正方向。

由于无法直接获得轻轨电车车辆计算参数，且已知该型车辆为南车株洲电力机车公司生产的100%低地板轻轨电车，因此结合国内学者对轻轨电车车辆动力性能的研究[9-11]，采用的车辆计算参数如表1所示。

根据表1取m1=1 044 kg，m2=7 292.75 kg，C=42.17 kN·s/m，k=615.38 kN/m，n=1,L=10.8 m代入动力微分方程中求解可得轻轨电车均布线荷载时程，时程曲线及荷载曲线见图3。

根据式(8)计算得出的是列车线荷载，没有考虑加载过程中空间位置的变化，因此在用于三维模型动力分析时还需要对线荷载进行简化和处理，处理方式在文献[3]也给出，即将线荷载人为转化为集中荷载再施加到单元节点上。

1.2 经验分析法

当不具备现场测试荷载或者建模计算受限时，国内外学者研究利用一个激振力函数来模拟列车动荷载，Jenkins、梁波、潘昌实等[12-14]采用一个能够反映轨道不平顺，附加动载和轨面波磨效应的激振力函数来模拟列车动荷载。

P(t)=P0+P1sinω1t+P2sinω2t+P3sinω3t

(9)

式中，P0为车轮静载；P1、P2、P3分别为对应于表2所示控制标准Ⅰ、Ⅱ、Ⅲ中典型值的振动荷载。Pi与列车簧下质量M0有关

Pi=M0aiωi

(10)

式中，M0为簧下质量；ωi=2πv/Li，v为列车运行速度，Li为相应于表2控制标准Ⅰ、Ⅱ、Ⅲ中的波长；ai为相应于表2控制标准Ⅰ、Ⅱ、Ⅲ中的矢高。

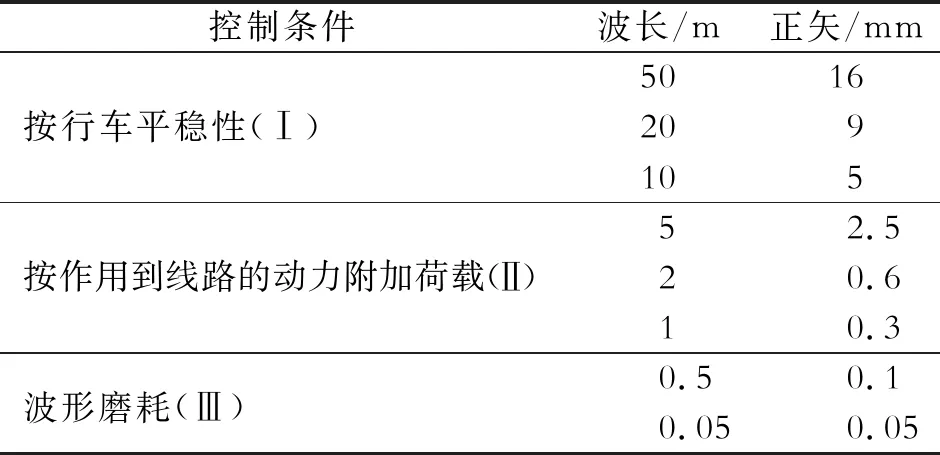
表2 轨道不平顺管理值

文献一般认为单轮静载取轴重的一半，考虑到模拟中将车轮简化为质点施加集中荷载到钢轨节点上，单边轴重由2个车轮分担，因此根据表1取P0=20 000 N，M0=522 kg，根据表2，选取较高标准，L1=10 m,a1=5×10-3m；L2=2 m,a2=6×10-4m；L3=0.5 m,a3=1×10-4m，取轻轨电车正常运营时速30 km/h代入式(9)，前4 s的模拟列车动荷载如图4所示。轻轨电车移动荷载的模拟如图5所示。

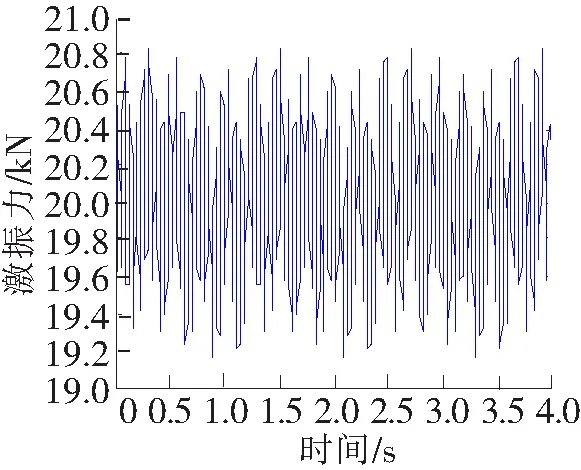
图4 激振力函数列车动荷载

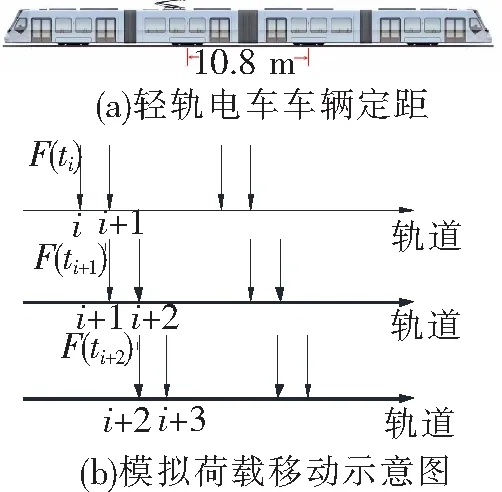
图5 轻轨电车移动荷载模拟

2 轨道-地基土结构数值模型

2.1 地基土计算假定及场地土参数

一般认为，列车引起地面振动时土体产生的应变值较小(ε<10-4)，土体的整体性没有遭受破坏且发生的形变能够恢复，土颗粒间相互位移消耗的能量很小，因此可将土体视为弹性体，提出连续介质、均质各向同性弹性体和小位移小形变假设。根据该轻轨电车建设施工时的地址勘探报告，将土层简化为3层，分别是人工填土、淤泥质粉细砂和碎屑岩残积土，各土层参数见表3。

表3 土层动力参数

2.2 轨道结构基本参数及模型确立

2.2.1 模型参数

三维模型全部用实体单元来模拟，选取solid45单元，钢轨弹性包覆材料选用solid185单元。可知该模型轨道结构各部分采用的材质，材料部分参数，截面型式及施工工艺，同时，参照已有的轻轨电车嵌入式轨道研究中的轨道结构基本参数[15-18]，最终将计算需要用到的材料参数列于表4。由于橡胶材料的超弹性体特性，采用Mooney-Rivlin模型来模拟橡胶材料，材料参数参考刘婷林[19]的研究成果，取值如下：C01/C10=0.25，d=2.5×10-5，轨下垫板和板下垫板：C10=10.667 MPa，C01=2.6 MPa；钢轨弹性包覆材料：C10=1.06 MPa，C01=0.26 MPa。

2.2.2 模型尺寸

模型尺寸侧重考虑采用杨永斌[20]和翟婉明[21]的建议来确定，杨永斌等[20]认为在分析地面高速列车引起的地面振动时，计算模型的宽度和深度应取感兴趣频率的剪切波波长λS的1～1.5倍；翟婉明[21]认为研究地面高速列车环境振动问题时，列车荷载作用范围边界距模型边界 30 m，认为边界条件对模型计算结果的影响可以消除。

关于沿轨道长度方向的尺寸，国内学者并没有做较为深入的探究，翟婉明[21]研究认为在激振力的作用下，轨道上前后10跨轨枕范围内将会受到振动影响，超出这一范围后振动的传播极弱，因此轨道长度可按车辆定距加上前后10跨轨枕的长度来计算。

综合上述，根据轨道结构对称性的性质，为了提高计算效率，三维模型将在轨道中心线处取半结构模型进行研究，建立模型尺寸为20 m×45 m×40 m(长×宽×高)，模拟轻轨电车两节车厢以30 km/h的速度运行时产生的环境振动，选取距离轨道中心线0 m、8 m、16 m和32 m 4个测点的铅垂方向振动数据进行研究，如图6所示。

2.2.3 单元尺寸

利用有限元建立模型的方法来分析列车引起的地面环境振动问题，实质上是将地面振动波在连续介质传播问题近似地用离散的单元组合模型来求解，这种通过将连续介质离散化来分析将会引起2种不利效应，称之为“低通效应”和“频散效应”。

文献[22]指出单元尺寸L=λS/12时可以取得精确的结果，当距离大于0.5λS后，单元尺寸扩大2倍在其他位置便可取得较为满意的结果。按照感兴趣的频率范围不同，λS是一个范围值，一般认为列车引起地面振动的频段在1～80 Hz。

和振兴[23]对地基土以边长0.5 m、2 m、3 m、6 m的8节点实体单元划分网格，地面中央用低频简谐波激励进行动力时程分析，结果表明，工况为边长0.5 m、2 m、3 m的地基土计算结果曲线基本重合，而边长为6 m的工况结果相差较大。综上所述，模型中，对线路附近的地基土单元尺寸取0.3 m，轨道结构单元尺寸取值更小，最小网格取0.06 m，随着离开线路的距离增加，单元网格逐渐加大，最大网格取4 m，有限元模型如图6所示。

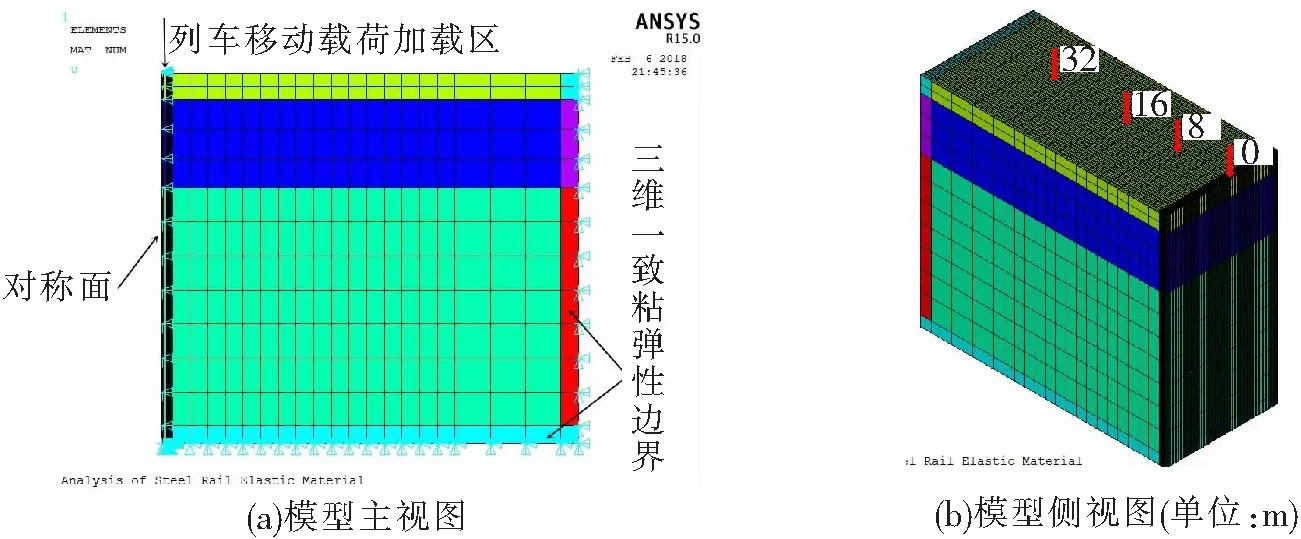
图6 轻轨电车环境振动有限元模型

2.2.4 边界条件

涉及到土体的有限元模拟时,不可能取无限大区域计算，需要设置人工边界条件消除人为边界对计算结果的影响， 本文采用谭辉等[24]提出的三维一致粘弹性人工边界。

3 结果分析

3.1 列车动荷载不同模拟方式对比

运用2种加载方式作对比分析，取轨道中部各测点模拟结果，算出加速度有效值和铅垂方向振级(VAL)列于表5、表6。选取钢轨和32 m处测点实测与模拟加速度时程图和幅值谱分析见图7、图8。

表5 列车动荷载不同模拟方式下加速度有效值 m/s2

表6 列车动荷载不同模拟方式下振级分析 dB

图7 钢轨振动加速度时程曲线及频谱图

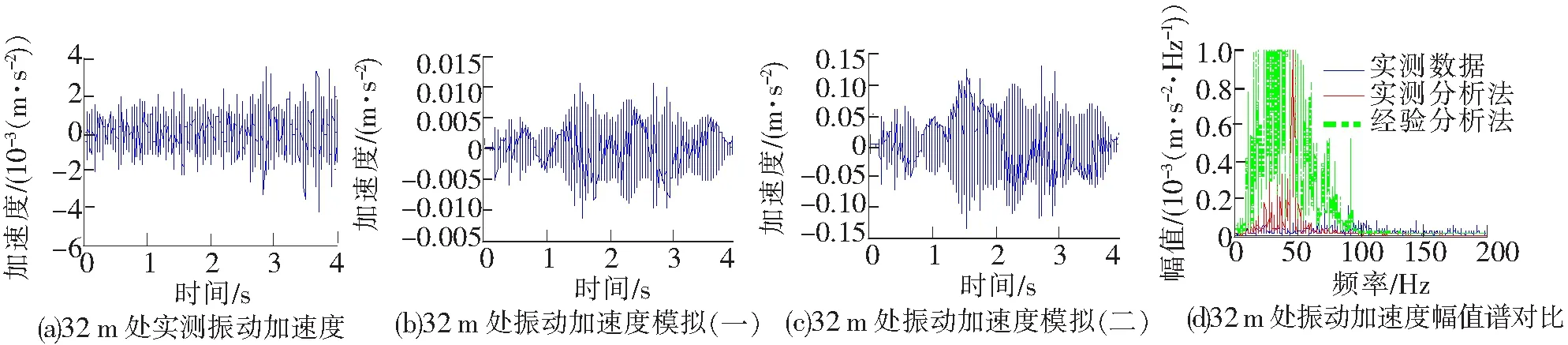
图8 32 m处振动加速度时程曲线及频谱图

根据采样定理频谱分析的频率范围在0～200 Hz，钢轨处振动成分集中频段基本对应，主要集中在80 Hz左右，但是通过模拟方法得到的频谱数据会偏大，主要在50 Hz、80 Hz、150 Hz和200 Hz这4个频段处，在实测数据中50 Hz和150 Hz这2个频段并无振动信号集中，这也体现了数值模拟的误差所在。在32 m处根据数值模拟得到的振动信号集中在50 Hz左右，而实测数据在该低频段并无明显集中现象，这是由于实测中环境作用的影响。

从时域数据上看，实测分析法模拟的测点振动加速度值与实测值较吻合，经验分析法的模拟值约偏大10倍，从数据分析所得的振级VAL上看，经验分析法所得的振级偏大，约20 dB，而实测分析法得到的振级数据较接近，最大偏差量约4 dB，从16 m和32 m测点的实测振级和模拟振级对比可以看出，由于实测环境中小山坡的存在，土层对环境振动的衰减作用极为明显。因此，为了尽量贴近实测数据，采用实测分析法模拟列车荷载来作不同钢轨包覆材料的减振性能模拟研究。

3.2 不同钢轨弹性包覆材料减振性能模拟结果

本节将进行不同钢轨弹性包覆材料减小环境振动效果的数值模拟对比，需要说明的是，某轻轨电车开工建设时，在地面线路钢轨上敷设了双块式、套靴式、嵌条式3种钢轨包覆材料。探究轻轨电车以正常时速(30 km/h)运行下的动力响应，为避免赘余，仅给出双块式包覆材料轨道模型铅垂方向振动加速度时程，见图9，各工况下加速度有效值随距离的变化见图10。

图9 模拟振动加速度曲线

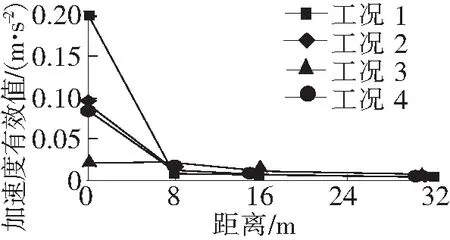
图10 模拟振动加速度有效值随距离变化

将有限元模拟获得的不同工况下的振动信号分析,可得到振动加速度级，并与实测值进行对比，将对比结果列于表7。

由图9、图10和表7可知，振动信号从轨道内传至轨道外时衰减约90%，而且没有发生振动放大现象，与实测数据衰减规律较符合，工况3振动信号衰减规律与实际情况有较大误差，道床处振动信号远小于实测数据，说明钢轨弹性包覆材料的截面形状对于其减振效果产生了较大的影响。

表7 振动加速度级模拟值与实测值对比 dB

分析其余工况，0 m和8 m处的模拟值与实测值吻合较好，其中在0 m处工况1比实测值偏大约5 dB，工况2和工况4均比实测值偏小约2 dB；在8 m处此三个工况与实测值吻合均较好，最大偏差约2 dB。根据前文分析可知，16 m和32 m测点模拟数值与实测值不匹配的原因是由于实测环境中地质条件的影响，故从振级数值上分析不具有对比性。因此，仅分析8 m处测点振级而对比不同工况的减振性能，可以看出工况1有较好的减振效果，并且与实测情况相符合。

结合实测值和模拟分析值说明当振动传至距离轨道中心线32 m时，工况1、工况2和工况4振级相差不大，最大差值约2dB，因此，可以说明从整体上看钢轨包覆材料的减振效果不明显。

将模拟得到的振动信号计算获取1/3倍频程图，可分析振级随频率的变化规律，并与实测分频振级进行对比(图11)。

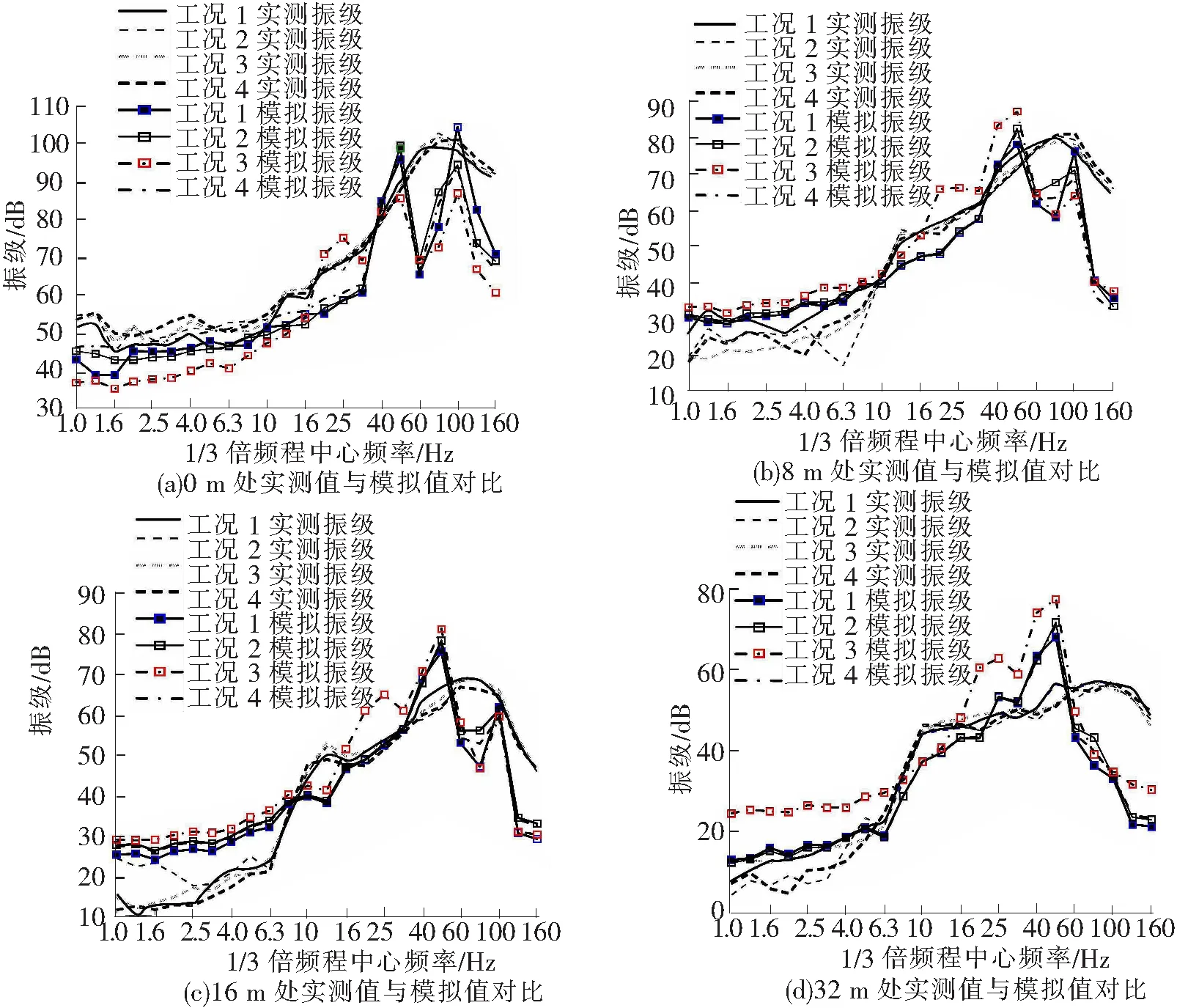
图11 各测点1/3倍频程曲线

由图11可知，模拟与实测得出的振动信号均集中在80 Hz左右，在低频段模拟与实测的4种工况均呈现了相同的规律性，钢轨包覆材料起到了较好的抑制振动效果，同时可以看到与实测曲线对比，有限元模拟存在误差。根据图中模拟数据与实测数据相结合，可以证实钢轨弹性包覆材料对抑制低频振动有较好的效果，对抑制高频振动效果较差甚至反而出现了轻微的放大现象。

4 结论

在实测获得的资料背景下并参考国内外相关文献，利用ANSYS有限元分析软件建立了4种工况下的三维轨道结构-土层有限元模型,并运用Matlab软件编程进行数据分析。通过合理设置模型参数，荷载模拟等措施，分析不同钢轨弹性包覆材料的减振效果并与实测数值进行对比，主要结论如下：

(1)根据轻轨电车同车型的车辆参数,可以确定实测分析法和经验分析法2种列车荷载模拟方法的计算参数,并将这2种方法运用到有限元模拟当中，相对于实测分析法，经验分析法获得的振动加速度数据与实测数据比较普遍偏大，因此实测分析法获得的模拟数据更贴近实测值。

(2)结合实测环境数据和模拟数据可得出结论：不同钢轨包覆材料的减振效果,在距轨道中心线8 m范围内能够较好体现，在此距离范围内双块式钢轨包覆材料的减振效果最好；当距离超过8 m后不同钢轨包覆材料下的振动响应与无设置钢轨包覆材料并无明显差异性。

(3)结合实测数据及数值模拟分析，钢轨弹性包覆材料对于抑制低频环境振动有较好的效果，对于抑制高频振动效果较差；对比3种钢轨包覆材料可知，其截面形状对于材料的减振性能有较大的影响。