钢轨轨腰缺陷检测MsT有限元分析及优化

郭 稳, 林知明

(1.华东交通大学 电气与自动化工程学院,江西 南昌 330013；2.华东交通大学 交通信息工程及控制研究所,江西 南昌 330013)

0 引言

钢轨是列车运行中必不可少的组成部件，但由于钢轨本身材料以及在使用过程中钢轨承受着来自列车直接作用力等原因都有可能使钢轨在轨腰处产生缺陷。随着列车的运行，轨腰缺陷进一步扩展，极大提高了断轨的可能性。为了保障人们乘坐轨道交通工具时的出行安全，防止列车在运行过程中断轨事故的发生，需要及时有效地对钢轨轨腰缺陷进行检测。

目前，国内外学者提出了多种无损检测技术与模型对钢轨缺陷进行检测[1-2]。孙继华等[3]和Kromine et al[4]将激光检测技术用于钢轨踏面裂纹检测，研究表明此方法可以有效检测钢轨踏面裂纹。文献[5]采用涡流检测技术对钢轨表面裂纹进行定量评估，但涡流检测技术穿透能力不足，只限于对钢轨表面缺陷检测。顾桂梅等[6]提出利用红外热波无损检测技术对钢轨轨脚两侧裂纹进行检测，但红外热波检测设备成本高且无法实现对缺陷深度的检测评估。苏日亮[7]针对钢轨轨底中心缺陷及两侧缺陷设计了2种不同的电磁超声检测模型，研究表明所设计的模型能够实现对钢轨轨底缺陷的检测。文献[8-9]提出一种基于感知振动信号的钢轨缺陷检测系统，但该系统只限于有限元模型。由上述可知，现有模型与研究方向主要集中在钢轨踏面及轨底缺陷的检测，鲜有针对轨腰缺陷提出的检测方法及仿真模型。

现根据磁致伸缩换能机理，将MsT用于钢轨轨腰缺陷检测并在钢轨内激发单向聚焦斜入射SV波(ULFSV波)。对MsT的激励、接收过程以及超声波在钢轨传播过程中与缺陷发生的相互作用进行了仿真分析。其中，发射线圈、接收线圈的提离距离和导线结构参数均会对缺陷回波信号产生影响。通过探究最优线圈参数组合达到优化MsT结构和提升缺陷检测能力的目的。该模型的建立对MsT用于钢轨轨腰缺陷检测及线圈优化设计研究具有指导意义。

1 理论分析

在电磁场作用下，铁磁性材料中超声波的运动方程为

(1)

式中，ρ为材料的介质密度；u为质点振动位移；c为刚度系数；fL为洛伦兹力；fMS为磁致伸缩力。本文主要研究磁致伸缩力对超声波的影响，忽略洛伦兹力的影响，即fL=0。

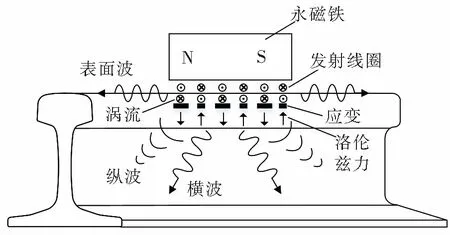
图1 钢轨中MsT激发超声波机理

钢轨中MsT激发超声波的机理如图1所示。永磁铁提供水平静磁场，当激励线圈中通入高频电流时，线圈周围产生交变磁场。静磁场会使钢轨集肤层产生恒定的磁致伸缩应变，交变磁场产生的应变会引起钢轨集肤层内质点周期性振动，从而在钢轨表面以及内部产生超声波。

在磁致伸缩换能过程中，钢轨的磁特性和机械特性与电磁场满足以下本构方程

(2)

式中，ε为应变张量;σ为应力张量;S为柔顺度矩阵;d为磁致伸缩系数;dT为逆磁致伸缩系数;μ为应力作用下的磁导率;H为磁场强度;B为磁感应强度。

当静磁场远大于交变磁场时，磁致伸缩系数d可认为是定值。此时的磁致伸缩系数d可以定义为[10]

(3)

式中，2个独立的磁致伸缩系数d11、d35可以通过磁致伸缩曲线计算获得。

(4)

式中，HS为静磁场。低碳钢的磁致伸缩曲线如图2所示，由公式(4)计算得到的磁致伸缩系数d11和d35的绝对值如图3所示。可以看出磁致伸缩系数与外部磁场的变化呈非线性变化的关系。

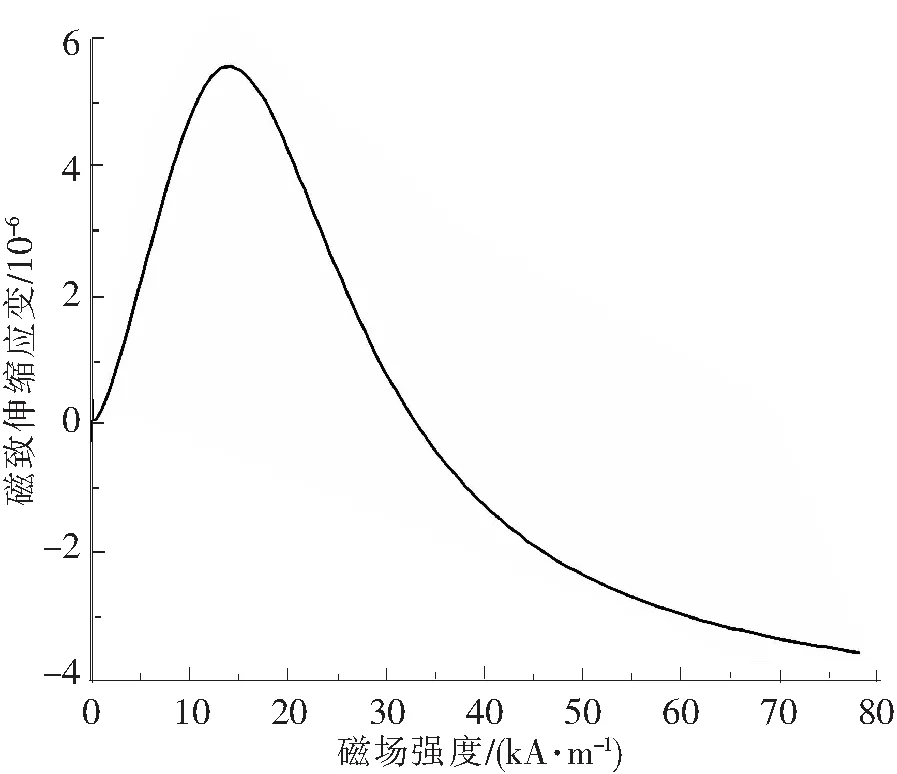
图2 低碳钢的磁致伸缩曲线

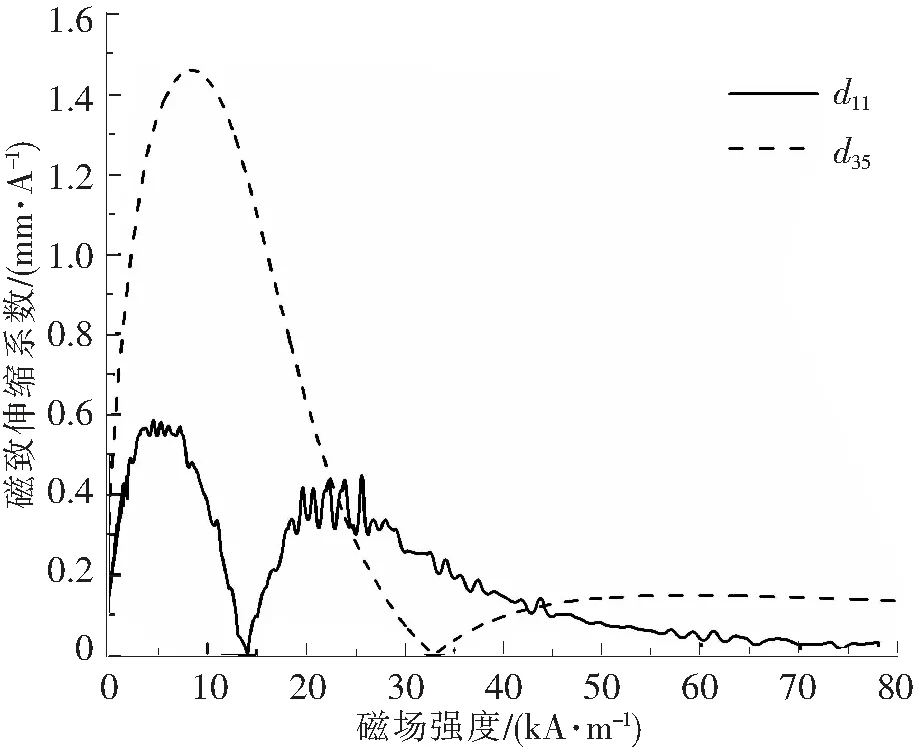
图3 磁致伸缩系数d11和d35的绝对值

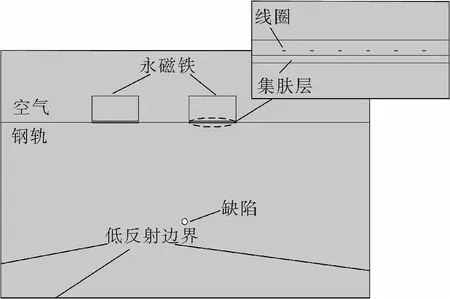
图4 MsT二维有限元模型示意图

2 MsT二维有限元建模

基于变分原理求解偏微分方程的有限元法广泛应用在各个研究领域。用有限元软件，建立钢轨轨腰缺陷检测MsT超声发射与接收过程的二维多物理场仿真模型，如图4所示。

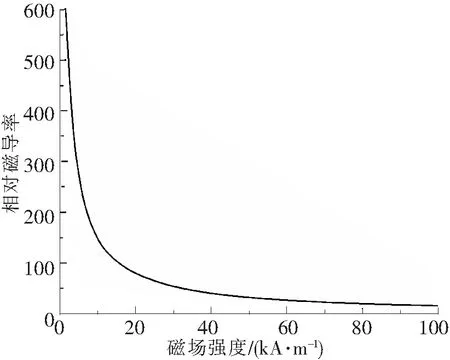
图5 相对磁导率曲线

MsT模型主要由空气、永磁体、发射线圈、接收线圈、钢轨以及钢轨集肤层的换能区域组成。根据GTS—60标准钢轨试块为原型进行二维建模，钢轨尺寸为432 mm×176 mm，杨氏模量为200 GP，泊松比为0.33，密度为7 850 kg/m3。钢轨集肤层深度为0.5 mm。在距离钢轨表面深97 mm处设置F6 mm的通孔来模拟钢轨轨腰缺陷。发射探头与接收探头的间距为100 mm。永磁铁尺寸为30 mm×20 mm，磁场强度为1.8 T。发射线圈采用双重叠曲折线圈，导线的线高a1为35 mm；线宽b1为0.2 mm；提离距离h1为0.3 mm；导线不等间距di。接收线圈采用单曲折线圈，其导线的线高a2、线宽b2以及提离距离h2均与发射线圈的导线参数相同，导线等间距d2为2 mm。有限元模型中材料电磁学参数如表1所示，钢轨的相对磁导率曲线如图5所示。为了减少钢轨左、右端面和底面的反射波对缺陷回波信号的影响，将钢轨的左、右端面以及底面设置为低反射边界。

表1 有限元模型中材料电磁学参数

为了在钢轨内激发ULFSV波，需要对发射线圈进行设计。MsT发射线圈的设计如图6所示。图6中，xi为第i导线距离最左端导线的距离，(xF,yF)为聚焦线坐标，θ为聚焦线初始角度，ri为第i根导线与聚焦线的距离。2个发射线圈A和B通入激励电流的相位相差π/2，其他参数相同，调整相邻导线之间的不等间距，可使SV波在θ方向处发生聚焦。发射线圈的激励电流如图7所示。

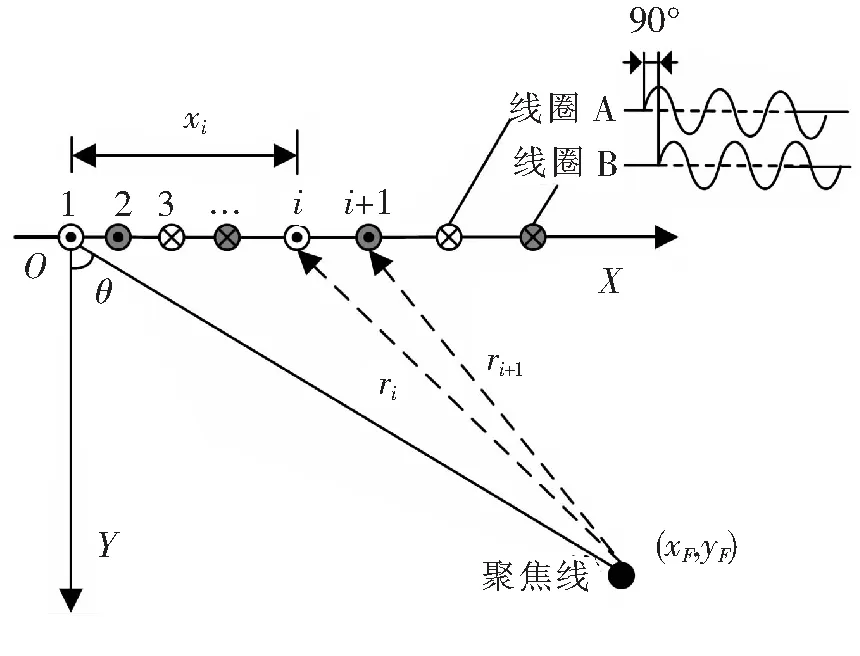
图6 发射线圈设计图

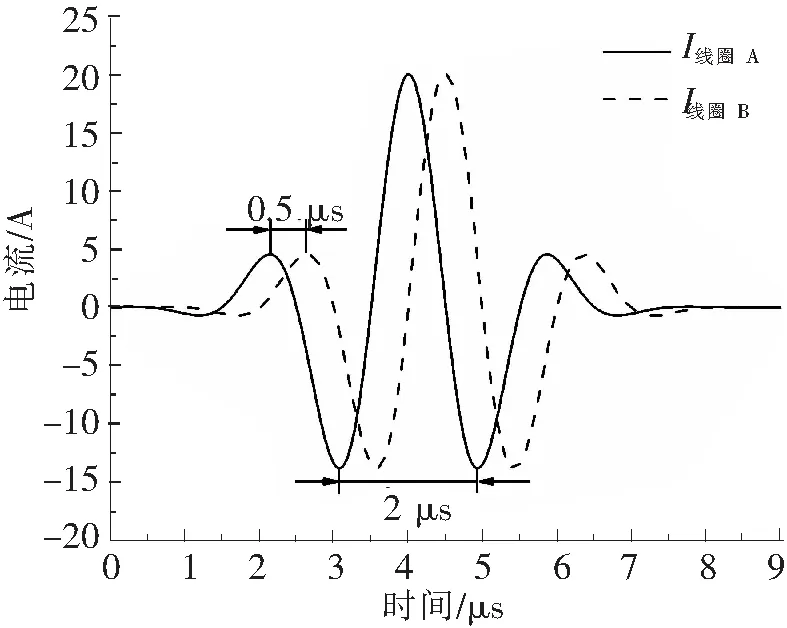
图7 发射线圈激励电流

2个发射线圈A和B的xi与ri满足如下方程[11]

(5)

设最左端导线坐标为(-110 mm，0.3 mm)， (xF，yF)=(-30 mm，-97 mm)，c=3 240 m/s，θ=50°，f=500 kHz。由式(5)计算得发射线圈的不等间距如图8所示。

为了保证模型建立的准确性，需要对线圈以及钢轨集肤层的换能区域进行局部网格细分。为了使有限元模型计算结果收敛，设置求解域的计算时间步长为1/(f×40)，钢轨集肤层换能区域的最大网格尺寸不超过SV波波长的1/10。对空气、永磁铁、线圈、钢轨以及钢轨集肤层换能区域进行不同大小的网格划分，分别设置为3、2、0.06、0.5、0.03 mm。有限元模型网格设计如图9所示。

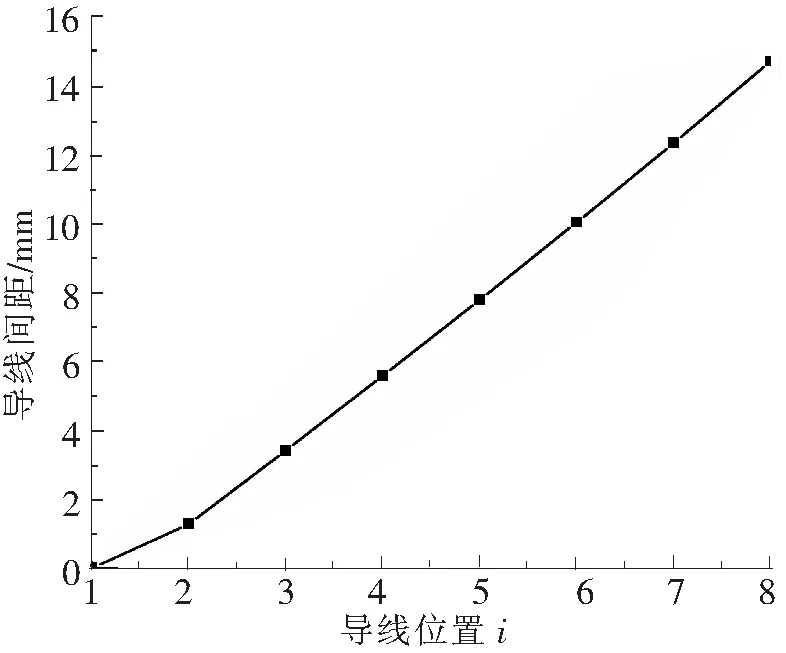
图8 发射线圈的不等间距

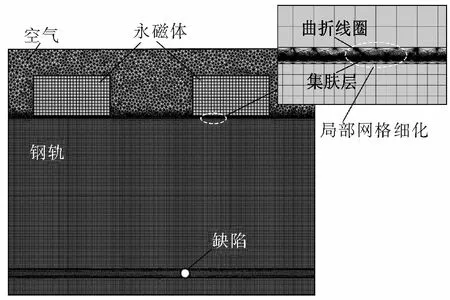
图9 有限元模型网格划分设计

3 仿真结果分析与优化设计

3.1 仿真结果分析

超声波在钢轨中的传播过程如图10所示。钢轨集肤层在水平静磁场与交变磁场共同作用下产生磁致伸缩效应，使其内部质点发生周期性振动产生沿着钢轨表面传播的表面波R波和临界折射纵波LCR波，由于通入2个发射线圈A和B电流的相位差以及相邻导线的不等间距，在钢轨内部产生纵波L波和单向聚焦斜入射SV波ULFSV波。

如图10(a)所示，可明显看到SV波在钢轨内部的一侧发生聚焦形成ULFSV波，另一侧减弱。如图10(b)所示，ULFSV波与缺陷发生作用，产生横波SS波(超声波发生反射)和纵波SL波(横波转换为纵波)。

轨腰中有缺陷时接收线圈的感应电压如图11所示。当轨腰中有缺陷时，接收线圈首先检测到LCR波和R波的感应电压，之后检测到缺陷回波(SL波、SS波)的感应电压幅值。缺陷回波的感应电压幅值比R波的幅值小很多，这是因为ULFSV波遇到缺陷时，大部分声波透过缺陷继续传播，只有少部分声波发生模式转换和被反射回来。设SL波的感应电压峰值为u1和SS波的感应电压峰值为u2。

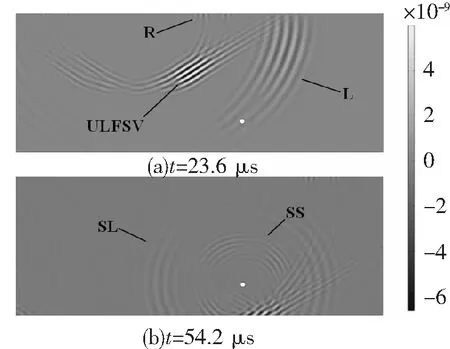
图10 超声波在钢轨中的传播过程

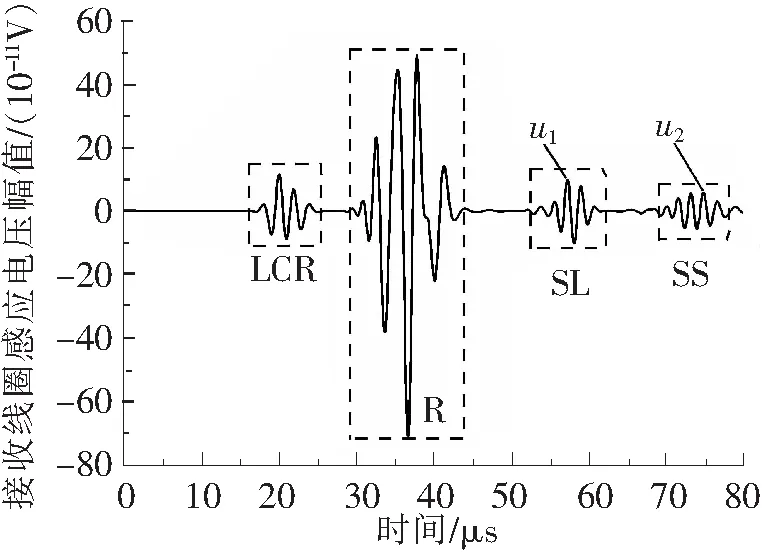
图11 钢轨轨腰缺陷的感应电压

3.2 发射线圈正交试验与优化

发射线圈导线高度、宽度及提离距离均会对u1、u2的幅值产生影响，有限元模型计算量较大，仿真时间长。采用正交试验的方法来减少试验次数，但同样可以分析出各个参数对u1、u2幅值的影响，并得出MsT发射线圈的最佳激励参数组合。在保证接收线圈的导线a2为35 mm、b2为0.2 mm、h2为0.3 mm不变的条件下，设定发射线圈导线参数的取值范围：a1为17.5～70.0 mm；b1为0.2～0.8 mm；h1为0.1～0.7 mm，将这3个因素各选取4个水平进行等分，正交试验表及仿真结果如表2所示。

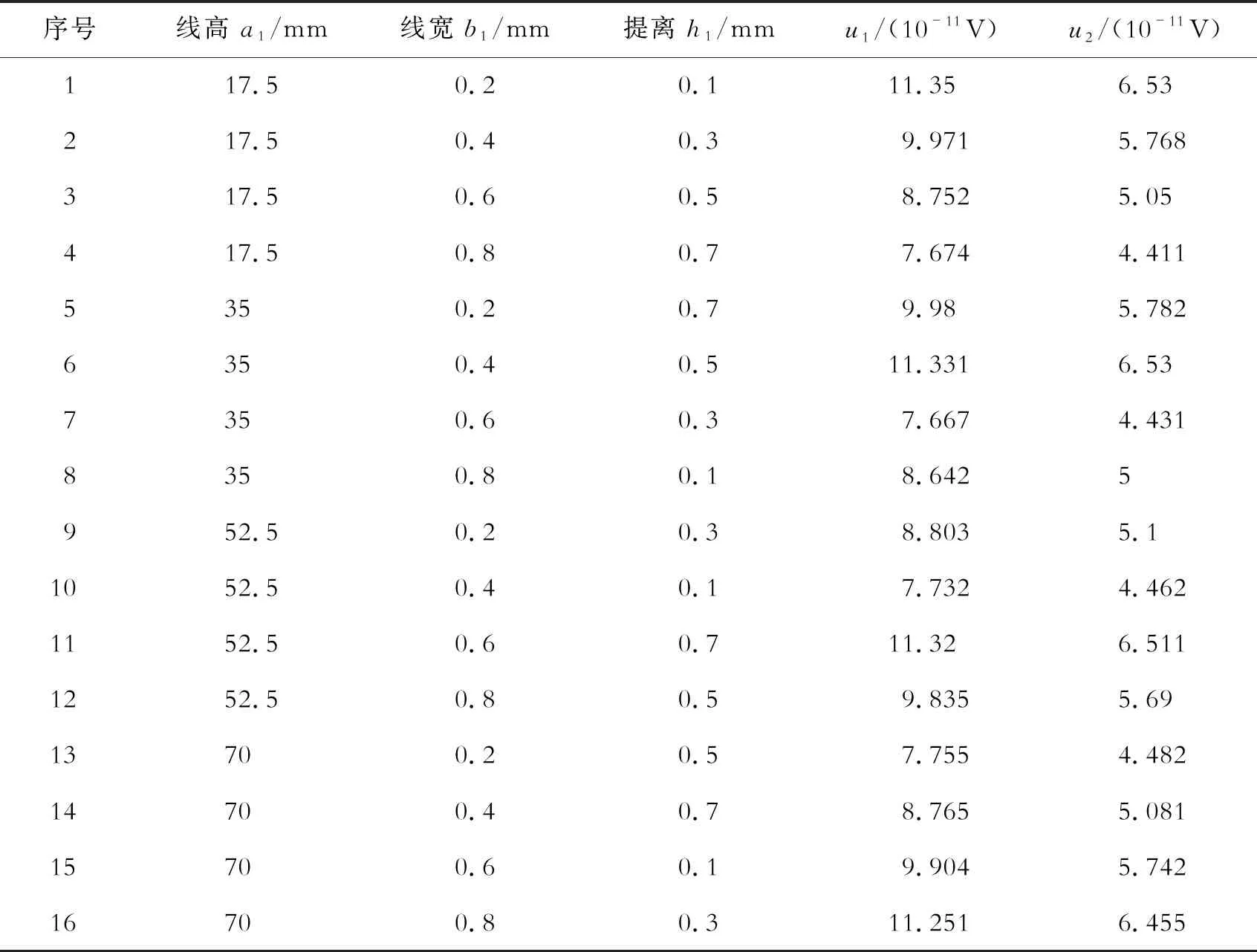
表2 发射线圈组合参数正交试验表及结果

发射线圈正交试验结果分析如表3所示。从表3可以看出，极差越大，表明该因素对u1和u2幅值影响越大。故这3个因素对u1和u2幅值影响排序相同均为h1>b1>a1。由图12可知，u1和u2的幅值都是随着发射线圈的导线高度a1增加，呈现出先减小后增大的趋势，但受a1的变化影响最小。随着导线宽度b1的增加，u1和u2的幅值在减小，但减小幅度不大。其中，u1和u2的幅值受提离距离h1的影响最为显著，随着提离距离h1增加，u1和u2幅值急剧减小。由图12(a)～图12(c)可得，对于u1的最佳激励参数组合：a1为17.5 mm；b1为0.2 mm；h1为0.1 mm。由图12(d)～图12(f)可得，对于u2的最佳激励参数组合：a1为52.5 mm；b1为0.2 mm；h1为0.1 mm。鉴于u1的幅值比u2高，更易于判断轨腰处是否存在缺陷，且导线高度相比于提离距离的影响非常小，最终选定发射线圈的最佳激励组合a1为17.5 mm；b1为0.2 mm；h1为0.1 mm。

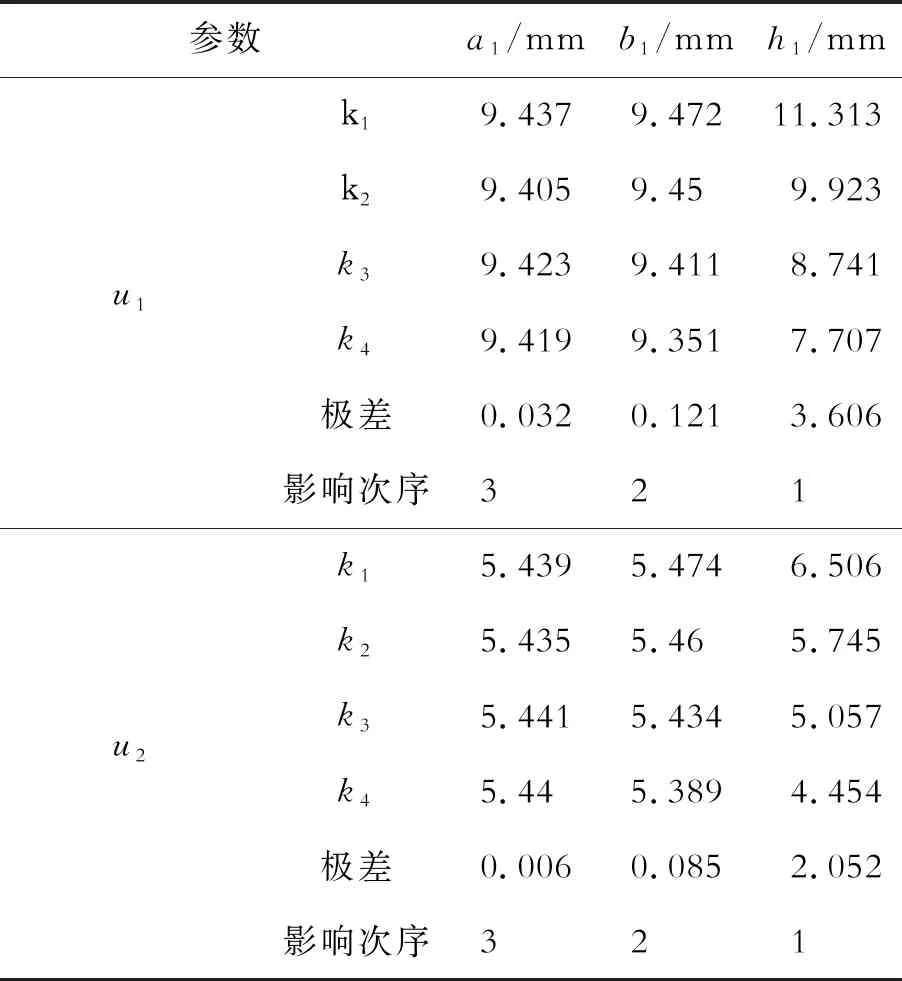
表3 发射线圈组合参数正交试验结果分析

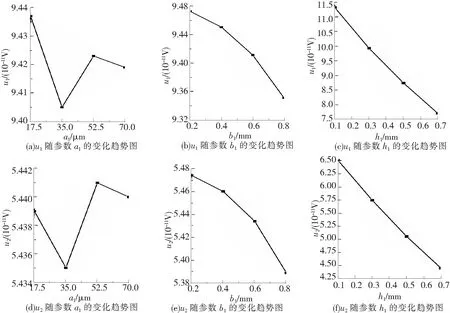
图12 u1、u2随参数a1、b1、h1的变化趋势图

3.3 接收线圈正交试验与优化

为了研究接收线圈导线高度、宽度及提离距离对u1和u2幅值的影响，在保证MsT发射线圈为最佳激励组合的条件下，设定接收线圈导线参数的取值范围a2为17.5～70.0 mm；b2为0.2～0.8 mm；h2为0.1～0.7 mm。将这3个因素同样各选取4个水平进行等分，正交试验表及仿真结果如表4所示。

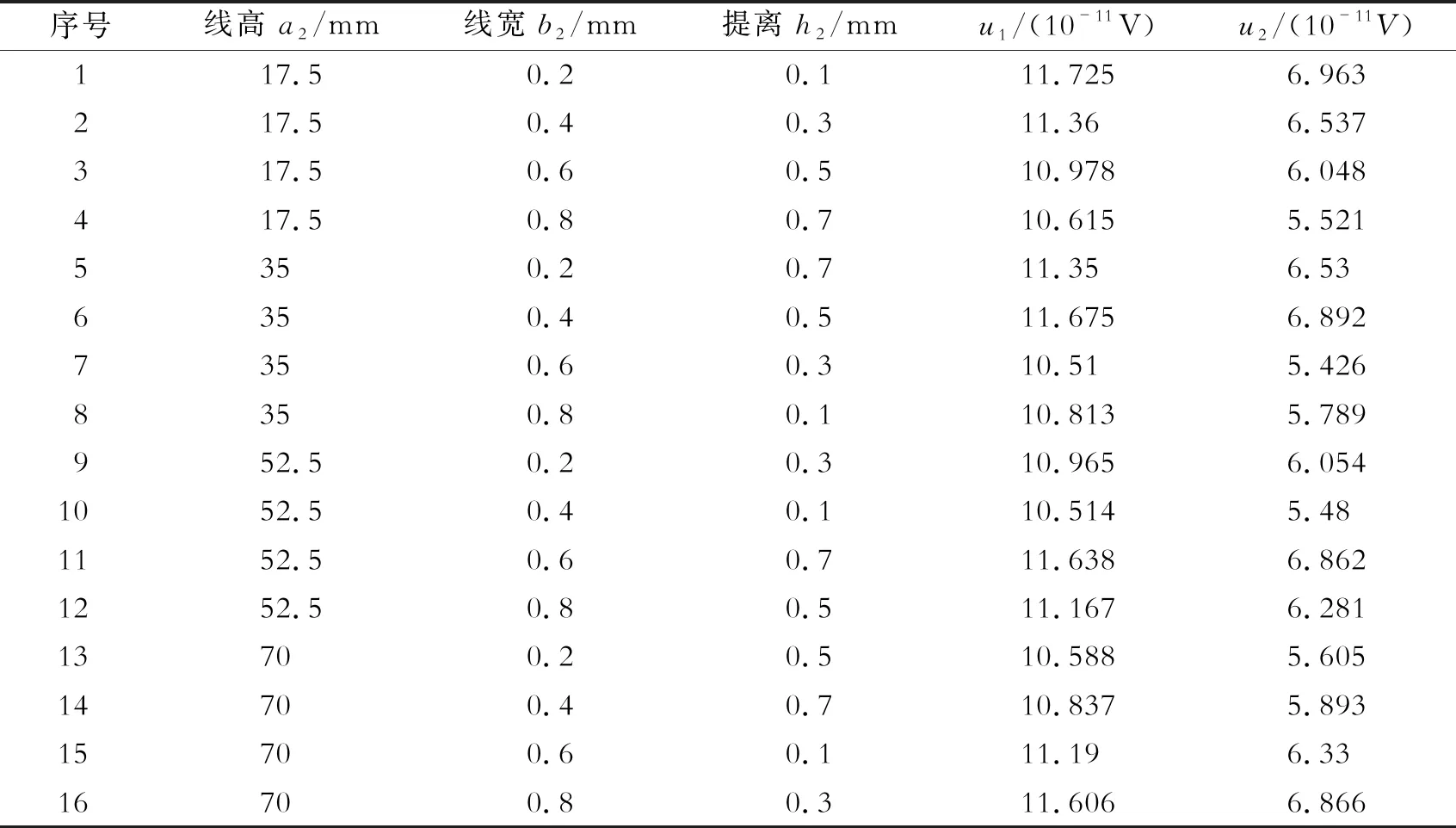
表4 接收线圈组合参数正交试验表及结果

接收线圈正交试验结果如表5所示。接收线圈导线的3个因素对u1幅值影响排序为h2>a2>b2，对u2幅值影响排序为h2>b2>a2。由图13可知，除了u2幅值随着线高a2的增加，呈现先减小后增大的趋势外，u1和u2幅值都随着接收线圈导线其余参数的增加而减小。由图13可得，接收线圈的最佳接收参数组合：a2为17.5 mm；b2为0.2 mm；h2为0.1 mm。

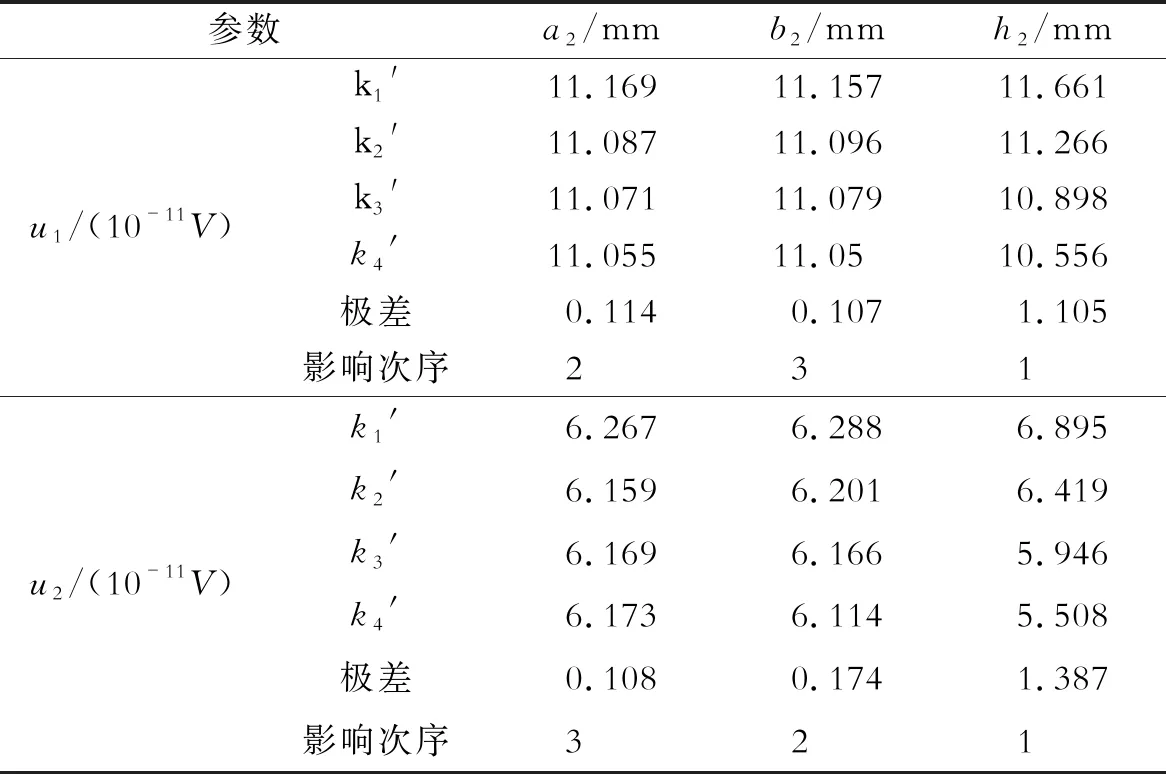
表5 接收组合参数正交试验结果分析

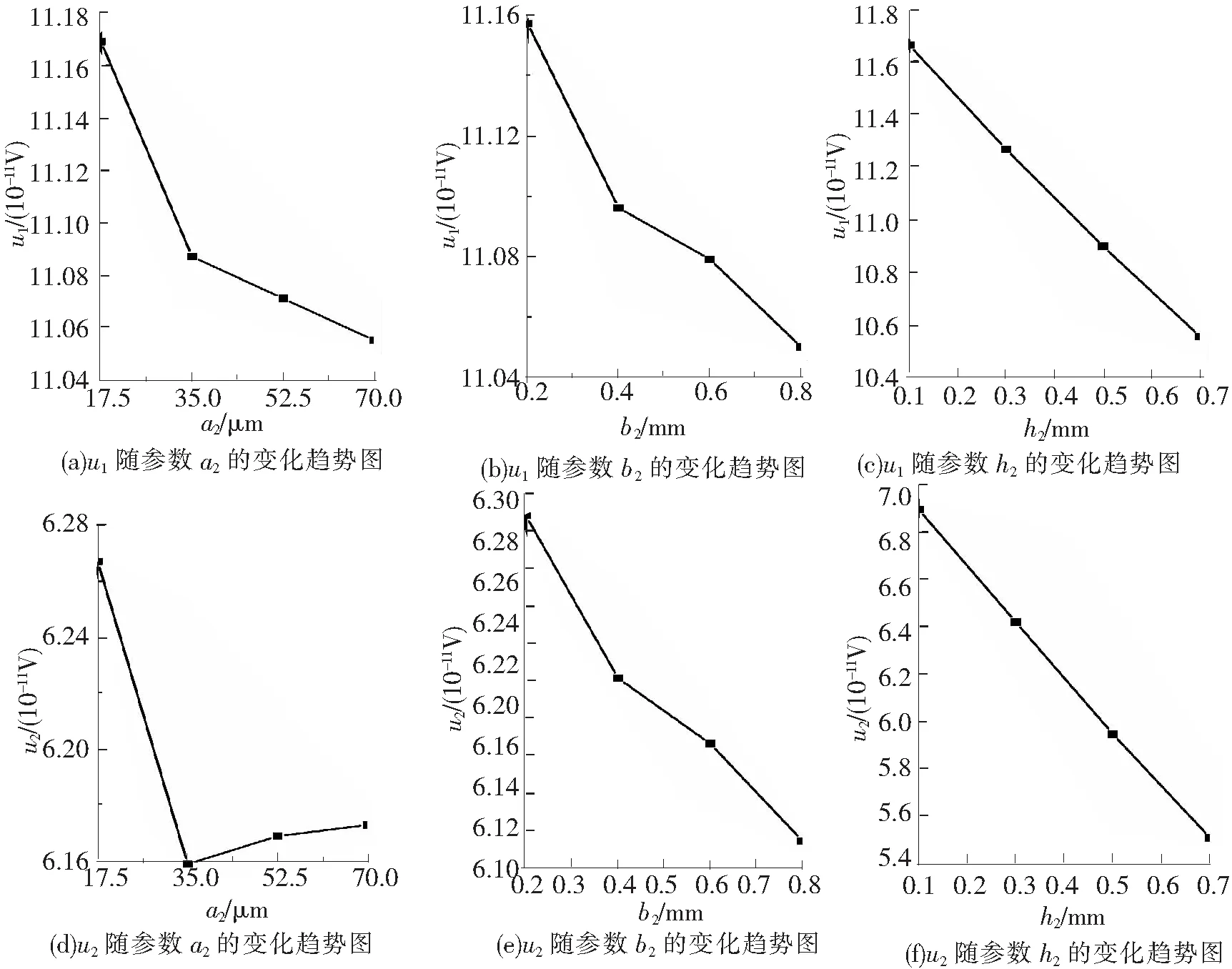
图13 u1、 u2随参数a2、b2、h2的变化趋势图

4 结论

利用有限元法，建立了包含ULFSV波激励、传播和接收全过程的钢轨轨腰缺陷检测MsT仿真模型。分别研究了发射线圈和接收线圈的导线高度、宽度以及提离距离对接收电压幅值的影响，通过优化线圈参数组合来优化MsT结构。在此模型的基础上，通过正交试验法，得到了提高MsT检测轨腰缺陷灵敏度的一般规律：

(1)发射线圈和接收线圈的提离距离对缺陷回波电压幅值的影响最大。提离距离越大，缺陷回波电压幅值越小，在MsT设计时，应尽量减小发射线圈和接收线圈的提离距离。

(2)发射线圈和接收线圈的导线高度对缺陷回波幅值均会存在一定的波动影响，但影响不大。

(3)发射线圈和接收线圈的导线宽度越小，缺陷回波幅值越大。

(4)相比于接收线圈组合参数的改变，缺陷回波幅值对发射线圈组合参数的改变更加敏感。