负刚度和空气弹簧并联的悬架系统的亚谐共振

曹计欢, 牛江川, 王 军

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

悬架系统是车辆的关键部件，决定着行驶过程中车辆的平顺性、平稳性和安全性。因此，近年来许多学者对悬架系统的动力学特性进行了研究。申永军等[1]利用最优控制理论对被动悬架的参数进行了优化设计，提升了车辆的运行性能。樊明辉等[2-3]利用平均法对含有分数阶微积分的线性单自由度和二自由度车辆悬架的动力学进行了理论分析。尹万建等[4]分析了在强迫激励下空气弹簧悬架系统的动力学特性，得到了空气弹簧的力学和数学模型，其刚度特性既包括线性刚度，又包括非线性刚度。韦鹏等[5]分析了分数阶duffing振子的亚谐共振，用平均法得到了系统的近似解析解，并得到了系统的稳定性条件。由于空气弹簧容易实现主动控制，因此空气弹簧悬架已经在客运汽车上广泛使用，并在一些高级轿车上开始应用，例如美国的林肯和德国的Benz600等轿车[6]。

近年来，负刚度的应用研究引起了学者们的注意。Paltus[7]首先将负刚度应用到隔振器件当中。高丽杰[8]研究了正负刚度关联情况下车辆座椅的隔振技术，分析了正负刚度并联机构的隔振原理，获得了良好的减震效果。纪晗等[9]提出基于负刚度原理减震系统和负刚度阻尼装置的2种实现思路，并详细分析了附加负刚度阻尼装置可以显著提高结构的减震效果。王维锐等[10]提出将负刚度控制策略用于半主动悬架的控制，并探讨了基于磁流变液减振器的半主动悬架的实现方法。侯广全等[11]应用负刚度原理来降低悬架系统的固有频率，从而降低系统的振动传递，改善车辆的平顺性。顾信忠等[12]研究了二自由度负刚度悬架系统的动力学特性及其对车辆平顺性和操纵性能的影响。

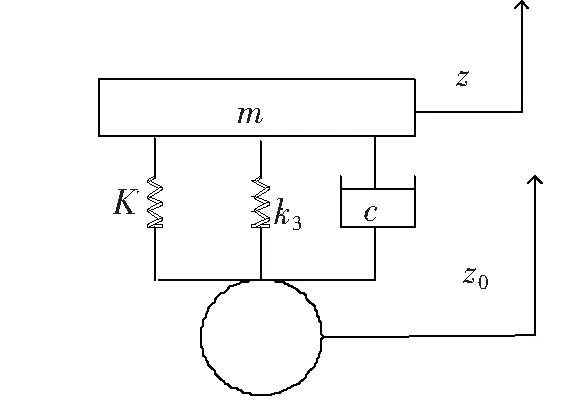
图1 1/4悬架系统模型

由于亚谐共振也会对车辆的性能造成较大的影响，因此有必要对悬架系统的亚谐共振进行研究，以避免共振的产生。现以负刚度和膜式空气弹簧并联的1/4悬架系统为研究对象，利用近似解析解分析负刚度和空气弹簧并联的车辆悬架系统的亚谐共振现象，并对稳态解的存在条件和稳定性进行分析。

1 近似解析解

研究如图1所示的负刚度和空气弹簧并联在一起的悬架系统，其中,c为考虑空气弹簧阻尼的悬架减振阻尼系数；z0为外部激励,z0=Z0coswt；m为簧上质量；z为悬架的垂向位移；k3为负刚度系数；K为空气弹簧的刚度系数，且空气弹簧的恢复力可以表示为[13]

K(z-z0)=k(z-z0)+k1(z-z0)2+k2(z-z0)3

(1)

式中，k为空气弹簧的线性刚度系数；k1、k2分别为空气弹簧的2、3次非线性刚度系数。

根据牛顿第二运动定律，可以得到悬架系统的运动方程

(2)

将式(1)代入到式 (2)中，可以得到

(3)

(4)

(5)

根据平均法，式(5)的解可以设为

x=acosφ+Bcos(ωt)

(6)

(7)

根据式(5)、式(6)和式(7)，可以得到

(8)

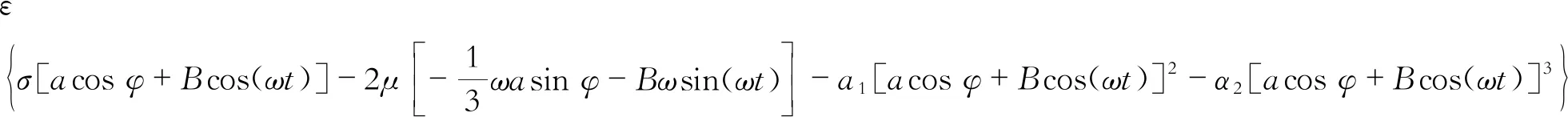
根据平均法，利用在一个周期内的平均值代替其慢变真值，则式(8)可改写为

(9)

经过计算，得到

(10)

将悬架系统的原参数代入到式(10)中，可以得到

(11)

根据式(6)和式(11)，则可以确定系统1/3次亚谐共振的近似解析解。

2 定常解的存在条件及稳定性分析

2.1 1/3次亚谐共振解的存在条件

(12)

(13)

以及相频响应方程

(14)

从式(13)和式(14)可以看出，系统的1/3次亚谐共振响应与空气弹簧的2次非线性刚度系数k1无关。将式(13)展开，整理后得到

(15)

A1ρ2+B1ρ+C1=0

(16)

由于A1>0和C1>0，根据一元二次方程根的判据公式以及韦达定理可知，式(16)存在正实根的条件为

(17)

因此，可以得到1/3次亚谐共振存在的必要条件为

(18)

(19)

由式(18)可知σ>0，说明1/3次亚谐共振发生在激励频率高于3ω0的范围内。将B=-9Z0/8代入到式(19)，可以得到

(20)

由式(20)可以看出，定常解存在的条件除了与外部激励频率有关以外，还与系统的阻尼、3次非线性刚度系数、线性刚度系数、负刚度系数以及外部激励的幅值有关，而且增大系统的阻尼可以避免1/3次亚谐共振的发生。

2.2 定常解的稳定性

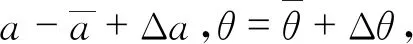
(21)

(22)

(23)

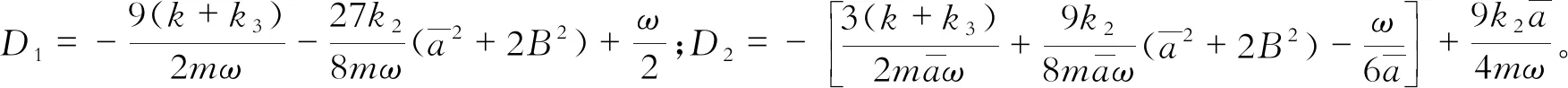
则可以得到系统的特征方程为

(24)

由于系统的阻尼c>0，因此可以得到定常解的稳定条件为

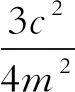
(25)

将B=-9Z0/8代入到式(25)，展开后并化简可以得到

(26)

由式(26)可知，当系统的幅频响应存在2个定常解时，上枝响应是渐进稳定，而下枝响应是不稳定的解[5]。在后续的分析中，主要研究系统的稳定解。

3 验证与分析

3.1 数值解验证

为了分析悬架系统的幅频响应特性，根据文献[13]选取悬架系统的参数，如表1所示。另外，外部激励幅值选取为Z0=0.08 m。

表1 悬架系统参数表

为了验证解析解的准确性，根据式(3)利用龙格库塔法得到系统的幅频响应曲线，结果显示在图2中。根据式(6)和式(13)利用近似解析解也可以得到系统的幅频响应曲线，也显示在图2中。在图2中，从系统的数值解可以看出系统不但存在明显的主共振，也存在1/3次亚谐共振响应。在亚谐共振区域，近似解析解和数值解的吻合程度较高，而且近似解析解的下枝响应曲线是不稳定的。

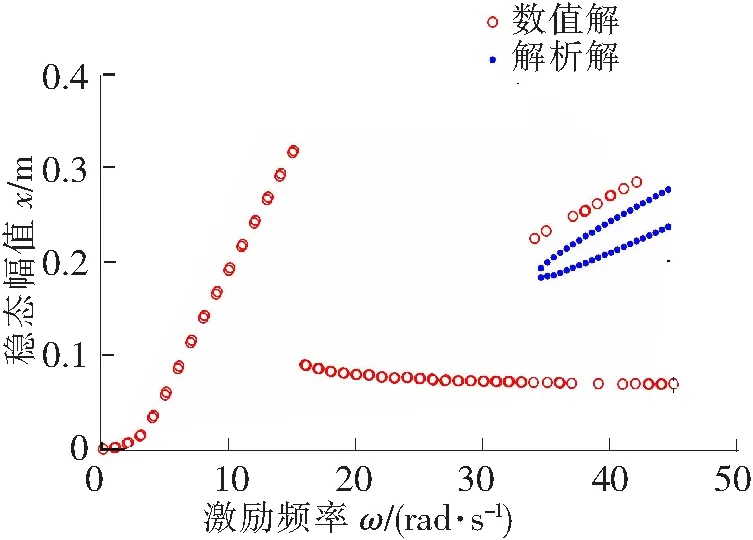
图2 数值解与解析解比较

3.2 负刚度对亚谐共振的影响

图3 负刚度对幅频响应的影响

分析负刚度对系统1/3次亚谐共振幅频响应的影响。分别选择k3=0，k3= -10 000 N/m,k3=-20 000 N/m，其他参数保持不变，利用近似解析解得到系统的幅频响应曲线，如图3所示。由于悬架系统中的空气弹簧的线性刚度k和负刚度k3可以合并处理，因此随着负刚度绝对值的增大，悬架系统的线性刚度逐渐减小，导致系统的固有频率也逐渐减小，产生1/3次亚谐共振的频率及其对应的幅值也会逐渐减小，但对相同的激励频率,其稳定的共振振幅是略有增大的。在存在亚谐共振的情况下，负刚度的引入虽然可以改善车辆的平顺性[11]，但也会导致亚谐共振行为的提前发生。

3.3 非线性刚度对亚谐共振的影响

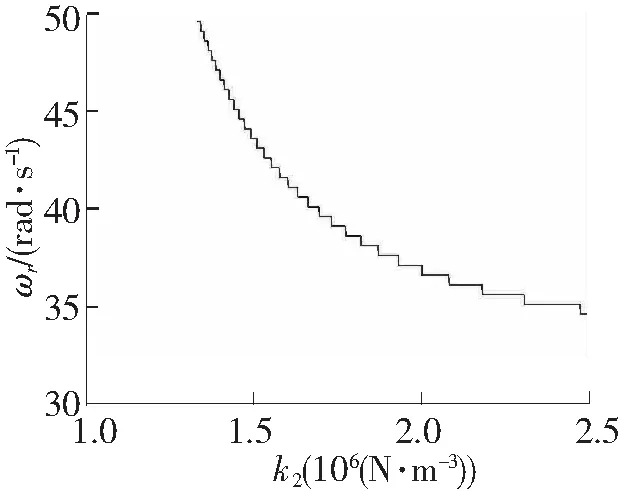
图4 非线性刚度k2对共振频率的影响

由于空气弹簧的2次非线性刚度系数k1对系统的1/3次亚谐共振幅频响应没有影响，在此分析空气弹簧的3次非线性刚度系数k2对幅频响应的影响。设系统发生1/3次亚谐共振的最小共振频率为ωr，其对应的共振幅值为xr。当3次非线性刚度系数从0到2 620 000 N/m3变化时，其他参数保持不变，利用近似解析解得到系统共振频率曲线以及共振幅值曲线， 分别如图4和图5所示。k2值分别选择2 220 000 N/m3、 2 420 000 N/m3、 2 620 000 N/m3，利用近似解析解得到系统的幅频响应曲线，如图6所示。从图4和图5中可以看出，当空气弹簧的非线性刚度系数k2增大到1 334 000 N/m3时，系统将会产生1/3次亚谐共振。此后，随着非线性刚度系数k2的增大，发生亚谐共振的频率及其对应的幅值都是减小的。从图6可以看出，当系统存在亚谐共振时，随着非线性刚度系数k2的增大，对于相同的激励频率，其对应的稳定的亚谐共振幅值是逐渐减小的。

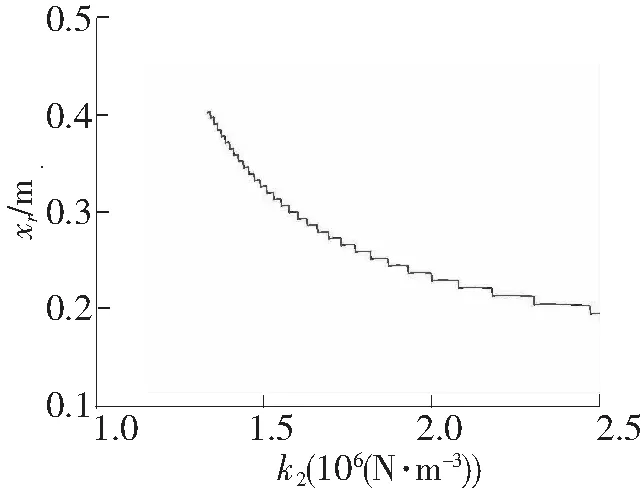
图5 非线性刚度k2对共振幅值的影响

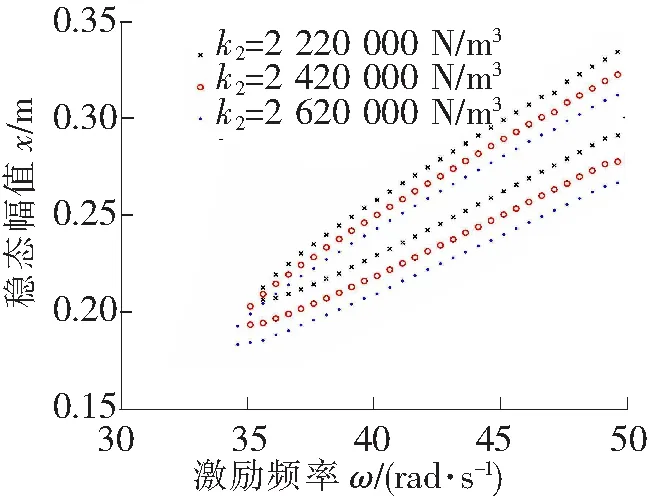
图6 非线性刚度k2对幅频响应的影响

3.4 阻尼对亚谐共振的影响

当系统的阻尼系数c从0到3 500 Ns/m变化时，其他参数保持不变，利用近似解析解得到系统最小共振频率曲线，如图7所示。c值分别选择2 000 Ns/m、2 500 Ns/m、3 000 Ns/m，利用近似解析解得到系统的幅频响应曲线，如图8所示。从图7中可以看出，随着阻尼系数c的增大，系统发生1/3次亚谐共振的最小共振频率逐渐增大。当系统的阻尼系数增大到3 390 Ns/m时，系统的1/3次亚谐共振将会消失。从图8中可以看出，当系统存在亚谐共振时，随着阻尼系数c的增大，对于相同的激励频率，其对应的稳定的亚谐共振幅值是逐渐减小的。

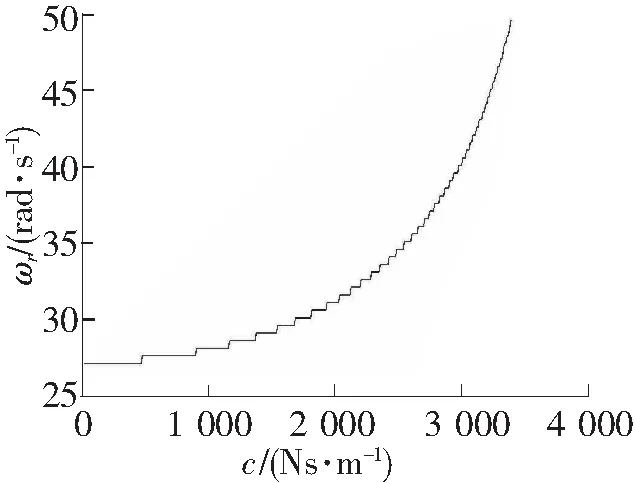
图7 阻尼c对共振频率的影响

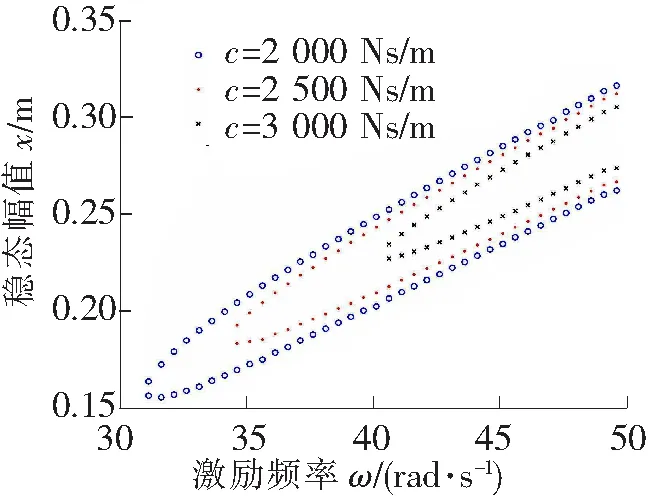
图8 阻尼c对幅频响应的影响

4 结论

研究了负刚度和膜式空气弹簧并联的单自由度悬架系统的1/3次亚谐共振。利用平均法得到了系统的近似解析解，并用龙格库塔法验证了解析解的正确性。分析了稳态定常解的存在条件以及稳定性。详细分析了负刚度、空气弹簧非线性刚度系数以及阻尼系数对系统幅频响应特性以及1/3次亚谐共振存在条件的影响。在文中给定参数的情况下，分析结果表明：随着负刚度绝对值的增大，可以降低系统的共振频率，但是会增大系统的1/3次亚谐共振幅值；空气弹簧的2次非线性刚度系数对1/3次亚谐共振响应没有影响；当空气弹簧的3次非线性刚度系数增大到一定程度，系统才会发生1/3次亚谐共振，而后随着非线性刚度系数的增大，对于相同的激励频率其共振振幅是逐渐减小的；随着阻尼系数的增大，对于相同的激励频率,其对应的亚谐共振幅值是逐渐减小的，当阻尼系数增大到一定程度，系统的1/3次亚谐共振将会消失。在并联负刚度进行悬架系统设计时，应该综合考虑系统参数的影响，尽量避免在恶劣路况下产生亚谐共振现象，以保证车辆的安全性。