舰炮输弹机供弹特性与误差分析
2020-11-16彭京徽张弘弨
彭京徽,李 超,董 理,张弘弨
(1.海军工程大学 兵器工程学院,湖北 武汉 430033;2.海军装备部,北京 100073;3. 海军研究院,北京 100161)
输弹机是大口径舰炮自动供弹机构的重要组成部分,其作用是将转弹终止位置的炮弹沿炮膛轴线方向快速、准确地推送到炮膛里。输弹终止位置关系到炮闩的关闩动作能否顺利完成,研究输弹终止的位置误差是进行自动供弹系统可靠性研究的必要条件,对提高机构运动可靠性和装备性能有着重要意义。国内已有学者对满足现代海战要求的含输弹机构的舰炮自动供弹系统展开了研究[1-9]。刘朋展等[10]针对弹丸姿态影响输弹可靠性与一致性问题,分析了影响弹丸姿态的因素;薛百文等[11]通过弹丸受力分析和建立运动方程,研究了底盘运动状态对弹丸在惯性输弹段的影响;郝驰宇等[12]利用RecurDyn软件和MFBD技术建立了输弹机刚柔耦合模型,得到不同位置时输弹机构的应力云图;顾宇涛等[13]则是利用RecurDyn软件对输弹机构故障进行分析;林通等[14]基于ADAMS建立考虑参数随机性的输弹过程动力学模型,进行了输弹机稳健优化设计研究;张鹏军等[15]对输弹机构动静两种状态受力分析,确定造成弹丸振动激励源的位置,利用传感器测试振动激励源点的振动幅值及频率并提出了消除输弹机振动的改进方案。
在以上研究的基础上,针对输弹机输弹时的机构运动问题,基于简化模型对机构进行受力和运动分析;建立机构运动方程并利用MATLAB进行算例分析;使用ADAMS样机试验分别研究了理想输弹和计及炮弹摩擦两种状态下的炮弹运动特性和弹体质心位置偏差变化情况。
1 输弹机工作机理与受力分析
1.1 输弹机结构和工作过程
输弹机结构如图1所示,主要由推力源、支架、齿轮组、固定齿条、滑轨、滑动齿条、推弹杆等组成,其工作机理是在动力源作用下推杆推动支架,安装在支架上的小齿轮受到固定齿条的约束进行逆时针转动,同齿轮轴带动大齿轮逆时针转动,进而与滑动齿条啮合,促使滑动齿条在滑轨上向前运动并带动推弹杆将炮弹向前沿炮膛轴线方向推进炮膛。
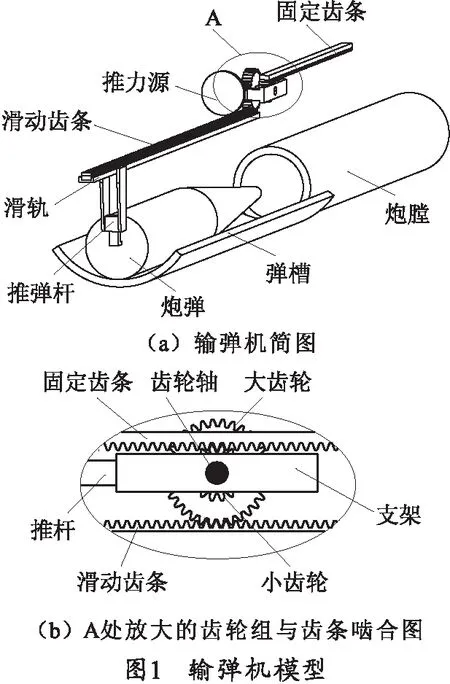
1.2 输弹机构受力分析
齿轮组受力如图2所示,推力F1驱使齿轮轴向前平动,小齿轮受到固定齿条约束在S1点以ω转速逆时针做啮合转动,进而带动大齿轮做相同运动,在S2点与滑动齿条啮合并给滑动齿条向前(右)的驱动速度v.此时,滑动齿条带动推弹杆运动,将炮弹输入膛内。图中R1、R2分别表示小齿轮和大齿轮的节圆半径;f是滑动齿条与滑轨间的摩擦力。
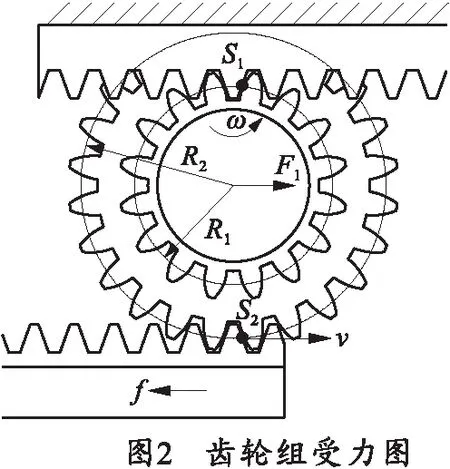
2 输弹机构的运动方程与算例分析
2.1 运动方程
由图2可知气缸给输弹机构的驱动力为F1;m0、m1、m2、m3、m4分别表示支架质量、齿轮组质量、滑动齿条质量、推弹杆质量和炮弹质量;g是重力加速度;X是支架运动行程;S是炮弹行程;fd是炮弹同弹槽和炮膛摩擦合力;J1是齿轮组的转动惯量;T是炮弹动能。
齿轮轴运动距离:
X=R1θ,
(1)
式中,θ表示转动角度。
S2点的加速度:
(2)
齿轮组受到的阻力矩:
(3)
齿轮组受到的阻力:
Ff=f+fd,
(4)
式中:f=μ1(m2+m3)g;fd=aμ2m4g+bμ3m4g,μ1、μ2和μ3分别是齿条与滑轨的摩擦系数、炮弹与弹槽的摩擦系数以及炮弹与炮膛的摩擦系数,a、b分别是弹槽摩擦力、炮膛摩擦力相对摩擦合力的占比。
mh=m2+m3+m4,
(5)
(6)
(7)
(8)
边界条件:
(9)
(10)
S=θR2,
(11)
(12)
式中:ω为转角速度;θ为转角;S为滑动齿条位移。
2.2 算例分析
为得到理想状态(忽略弹体摩擦)齿轮组速度和弹体动能变化情况,分别取:
F1=1 200cos(πt/1.6);R1=0.02 m;R2=0.04 m;m0=0.9 kg;m1=1.0 kg;m2=4 kg;m3=0.5 kg;m4=40 kg;J1=0.006 N·m;S=1.12 m;μ1=μ2=μ3=0;g=10 m/s2.
2.2.1 齿轮组运动速度
齿轮与齿条啮合会产出齿轮接触力,受力与传动如图3所示。
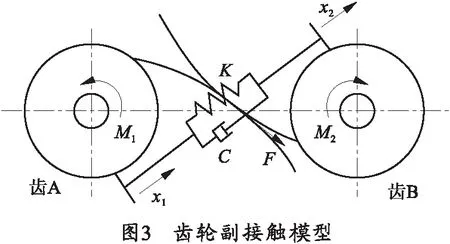
齿A与齿B啮合时,不仅存在法向的正碰撞,也存在切向的摩擦。对法向正碰撞建立等效弹簧阻尼模型模拟实际情况,过程中产生的碰撞力用弹簧力等效,能量损失利用阻尼器来模拟。切向摩擦存在两种状态:滑动和粘滞,分别使用库伦摩擦定律求解滑动时的切向力,以滑动摩擦力与弹性变形力的粘性合力求解粘滞状态摩擦力[16]。
在ADAMS样机中分别对小齿轮和固定齿条、大齿轮与滑动齿条施加contact接触力。利用MATLAB绘制齿轮组的计算速度变化曲线,由ADAMS样机导出得到的仿真速度曲线(包括是否考虑弹体摩擦两种情况),如图4所示。由图4可知,齿轮组仿真速度在运动起始阶段存在突变,之后仿真曲线受齿轮与齿条啮合的影响速度存在波动现象,但仿真速度与计算速度存在一定的误差,在不计及弹体与弹槽和炮膛的摩擦时,输弹截止时间仿真为640 ms,计算时间为481.3 ms,时间误差158.7 ms,其误差主要来源于齿轮组与齿条的摩擦。在计及弹体与弹槽和炮膛的摩擦时,在弹体还未与炮膛产生摩擦时,弹体与弹槽的摩擦对弹体运动速度影响较小,输弹截止时间仿真为714 ms,与不计及弹体摩擦时误差74 ms,其误差主要来自炮膛和弹体的摩擦。
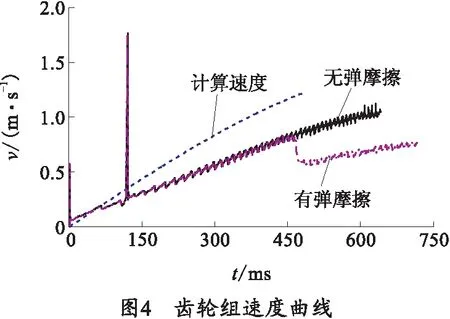
2.2.2 弹体动能变化
由MATLAB和ADAMS进行分析,分别得到图5所示的弹体计算动能变化曲线和仿真动能变化曲线。

由图5可知,弹体动能计算曲线与仿真曲线的误差同齿轮组速度误差和运动截止时间误差保持一致,因此在输弹机工作时应对齿轮组保持良好的润滑条件,以降低摩擦带来的影响。
3 输弹运动误差分析
供弹机构设计以循环图为基础,以子系统交接弹体的时间和空间位置为节点,建立造成节点偏差模型和供弹系统的误差模型,其中,二维时间t和空间位置P的误差模型如图6所示。图中P1是理想机构运动位置,P2与P3分别是实际机构运动位置,r是机构可接受的最大运动误差范围。在输弹运动中如果炮弹轴线与炮膛轴线偏离太大,会造成弹体与炮膛壁产生碰撞,影响输弹机的寿命和导致输弹动作的失败。

3.1 弹体运动与位置误差
由虚拟样机仿真得到如图7所示的不计及弹体摩擦和计及弹体摩擦时输弹运动的弹体质心位置变化曲线,在图中分别用虚线和实线表示。
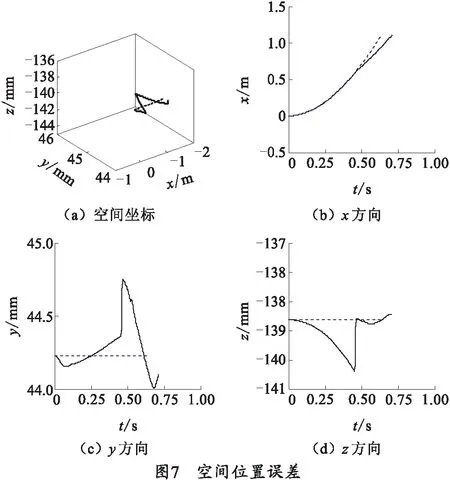
由图7可知,在输弹运弹体进入炮膛前,两种状态在x方向上的距离误差很小,进入炮膛后,随时间增加而误差变大,待不计及弹体摩擦输弹结束后,误差逐渐变小;在y、z两个方向上,弹体质心存在偏离轴线的现象,并在炮弹开始入膛后质心偏移明显变小,但y方向在进入炮膛时有突变。

同时,可得到两种状态的弹体质心的空间位置误差变化曲线,如图8所示。 由图8可知在不同运动条件下,弹体在运动过程中位置误差可能较大,但是最终输弹结束时炮弹位置误差可以很小,仅0.379 7 mm.
3.2 弹体运动与时间误差
根据两种状态条件下输弹运动和时间的关系,绘制炮弹轴线方向行程与运动时间的关系曲线,如图9所示,并得到其输弹时间误差值。

由图9可知有无弹体摩擦的输弹结束时间t1和t2分别为0.714 s和0.640 s,输弹时间误差0.074 s;且由图9可得知,弹体与炮膛的摩擦力和弹体与弹槽的摩擦力相比,前者对输弹影响更大。
4 结论
在水平输弹条件下,基于理论计算和样机仿真分析,得到了齿轮组的速度和炮弹动能变化情况,并在上述研究的基础上,对输弹运动过程中弹体运动特性进行了研究,得到了不计及弹体摩擦和计及弹体摩擦时的质心位置误差和输弹时间误差。结果表明:
1)由理论推导计算的齿轮组速度和弹体动能变化与样机仿真结果对比可知,齿轮副摩擦、弹体与炮膛摩擦对输弹有较大影响。
2)输弹过程中炮弹质心存在偏移的情况,且在炮弹开始入膛后质心偏移明显变小,但输弹结束时仍存在0.379 7 mm的质心位置误差。
3)弹体与炮膛的摩擦力比弹体与弹槽的摩擦力对输弹时间误差的影响更大。
