飞蛾扑火优化算法在聚类分析中的应用

李志明

(广西科技师范学院 数学与计算机科学学院，广西 来宾 546199)

0 引 言

聚类[1]是一种流行的数据分析和数据挖掘技术。聚类分析是一种无监督的学习过程，它的任务是将类似的对象分组成多个类组。简单的说，聚类分析问题的任务就是把一些对象按照某种规则分成不同的组，分组完成之后，每个组里面的对象具有较高的相似度，而不同组之间的对象具有较高的相异性。聚类算法是基于样本之间距离或相似性的自动分类，且聚类技术已经成功应用于诸多实际的问题当中，如数据挖掘[2]、模式识别[3]、图像分割[4-5]等。分组聚类方法是指通过优化某些标准将数据划分成预定数量的簇。K-means是最流行的分组聚类方法[6-7]，不过K-means高度依赖于初始状态，并且容易陷入局部最优。

为了有效地解决聚类分析问题，国内外一些学者尝试用新兴的群智能算法来求解这类问题。2011年，Hatamlou等采用了一个大爆炸算法进行数据聚类[8]；2014年，陈信等提出一种改进型猴群算法，并将其应用到聚类分析中，取得了比K-means等更好的性能[9]；2015年，张森等将新型灰狼优化算法应用于聚类分析中，取得了良好的成绩[10]；2016年，王睿将基于蜜蜂传粉策略的花授粉算法用于求解聚类分析问题，均取得了很好的成绩[11]；2019年，凌静等提出结合模拟退火算法的K-means聚类方法，其聚类准确性比一般K-means方法和遗传K-means方法都要高[12]。

1 飞蛾扑火优化算法

飞蛾扑火优化算法(moth-flame optimization，MFO)是由学者Mirjalili于2015年提出的一种新型群智能优化算法，其灵感来源于一种特殊的导航机制——横向定位导航机制[13-14]。飞蛾在晚上飞行时，因其与月亮相距较远，所以飞蛾与月亮保持固定的角度即可保证自己沿直线飞行。

然而在现实中，飞蛾与火焰相距很近，当飞蛾看到火焰发出的光时，便会试图与其保持固定的角度飞行，而由于这些人造光相比月亮光距离很近，所以，飞蛾仍然保持与人造光的固定角度不变飞行时，飞蛾便会最终向人造光处收敛。

在MFO算法中飞蛾是候选解，飞蛾的集合用矩阵M表示，OM存储相对应的适应度值。算法中另外一个核心组件火焰用F表示，OF存储相对应的适应度值，并且矩阵M和F具有相同的维数。在MFO算法中，飞蛾或火焰都是解，它们的不同就在于每一次迭代过程中更新方式的不同。飞蛾在搜索空间里是实际的搜索主体，而火焰为当前获取的最佳位置。因此，每个飞蛾都会搜索一个火焰，在找到更好的解的情况下进行标记并更新，通过这种机制，飞蛾永远不会失去它的最优解。

MFO算法用全局最佳的三元组表示如下：

MFO=(I,P,T)

(1)

通过函数I随机产生一个飞蛾种群及相应的适应度值，其模型如下：

I:φ→{M,OM}

(2)

P是使飞蛾在搜索空间里移动的主函数，它接受矩阵M，并返回更新后的值。

P:M→M

(3)

当满足终止准则时，T函数为真；如果不满足，则T函数为假。

T:M→{true,false}

(4)

I函数初始化之后，P函数迭代运行直到T函数返回真。为了精确地模拟飞蛾的行为，可使用下式对飞蛾相对于火焰的位置进行更新。

Mi=S(Mi,Fj)

(5)

其中，Mi为第i只飞蛾，Fj为第j个火焰，S为螺旋形函数。

选取对数螺旋线作为飞蛾的主要更新机制，其对数螺线描述如下：

S(Mi,Fj)=Di·ebt·cos(2πt)+Fj

(6)

其中，Di为第i个飞蛾与第j个火焰的距离，b为定义对数螺旋线形状的常数，t为区间[-1，1]上的随机数。其中D由式(7)计算求得。

Di=|Fj-Mi|

(7)

式(6)模拟了飞蛾的移动路径，并可以确定飞蛾的下一个位置。参数t定义为飞蛾在下一个位置应当接近火焰的程度(t=-1是最接近火焰的位置，t=1为距离火焰最远的位置)。在式(6)中仅仅需要飞蛾朝向火焰移动，却也容易使MFO算法陷入局部最优。为了避免这种情况，每个飞蛾必须使用式(6)中的火焰来更新它们的位置。每次更新火焰列表后，火焰便会根据它们的适应度值来排序，然后飞蛾更新它们相对于相应火焰的位置。第一只飞蛾总是更新相对于最优火焰的位置，而最后一只飞蛾更新列表中相对于最差火焰的位置。

针对在搜索空间中相对于n个不同位置飞蛾的位置更新，有可能降低了最有希望解的开采，提出一种适合于火焰数量的自适应机制。使用式(8)使火焰数量在迭代过程中自适应减少：

(8)

其中，l为当前迭代次数，N为火焰数量的最大值，T为最大迭代次数。

2 基于单纯形法的飞蛾扑火优化算法流程

单纯形法又称为可变多面体搜索法，它具有计算量小、搜索速度快等优点，是一种传统的处理无约束最优化问题的方法。在标准飞蛾扑火优化算法的基础上使用单纯形法搜索策略，可以增强算法的种群多样性，使算法寻找到更好的位置。SMMFO算法的简易流程如下：

Initialize the position of moths

While(Iteration<=Max_iteration)

Update flame no using Eq.(8)

OM=FitnessFunction(M);

if iteration==1

F=sort(M);

OF=sort(OM);

else

F=sort(Mt-1,Mt);

OF=sort(Mt-1,Mt);

end

for i = 1:n

for j=1:d

Update r and t

Calculate D using Eq.(7) with respect to the corresponding moth

Update M(i,j) using Eqs.(5) and (6) with respect to the corresponding moth

end

for each search agent

Update the position of the current search agent using Simplex Method

end

end

3 仿真实验

3.1 仿真环境

为了验证SMMFO在解决聚类分析问题上的有效性，选取了8个常见的数据集，其中包括2个人工数据集和6个现实数据集[11]。

8个数据集描述如下(数据集中数据项个数为N，每条数据的属性数为d，数据集要分类的数目为K)。人工数据集1(N=250，d=3，K=5)中的每个属性值都服从均匀分布，即分别服从(85,100)、(70,85)、(55,70)、(40,55)和(25,40)上的均匀分布。人工数据集2(N=600，d=2，K=4)，其中的600条数据项中的属性值均服从二维随机分布。Iris数据集(N=150，d=4，K=3)来自于150个随机样本，每条数据由四个属性构成。Wine数据集(N=178，d=13，K=3)取自于对意大利相同地区的三种不同品种的酒进行化学分析，共有178条数据项，每个数据项有13个属性。Seeds数据集(N=210，d=7，K=3)，共有210个数据项，每项数据包含7个属性，并且可分为3类，每类各含有70条数据集。Heart数据集(N=270，d=13，K=2)包含270个数据项，每个数据项包含13个属性，该Heart数据集来源于心脏病数据库，不过采用了不同的表达形式。Balance Scale数据集(N=625，d=4，K=3)根据平衡性分为向左倾斜、向右倾斜和平衡居中3类，每条数据项有left weight，left distance，right weight，right distance等4个属性，根据两个比重left weight×left distance和right weight×right distance的大小对数据项进行分类，若前者大，则该数据项为向左倾斜，若后者大，数据项为向右倾斜，否则数据项被归到平衡居中里。Contraceptive Method Choice (CMC)数据集(N=1 473，d=10，K=3)为避孕方法选择集，该数据集源自于1987年印度尼西亚进行的全国避孕患病率调查的一个样本，目的是预测当前的避孕方法是无效的、短期有效的还是长期有效的。

以上8个数据集均有自己的特点，因此，对它们的实验结果数据能充分反映算法的性能。另外，还选取了PSO[15]、ABC[16]、GGSA[17]、CS[18]等算法作为比较算法。

3.2 实验结果与分析

各实验结果如表1～表8所示，记录了每个算法取得的最优值、最差值、平均值、标准差。从各表可以看出，在求解这8个测试集时，SMMFO均表现出了较好的性能。

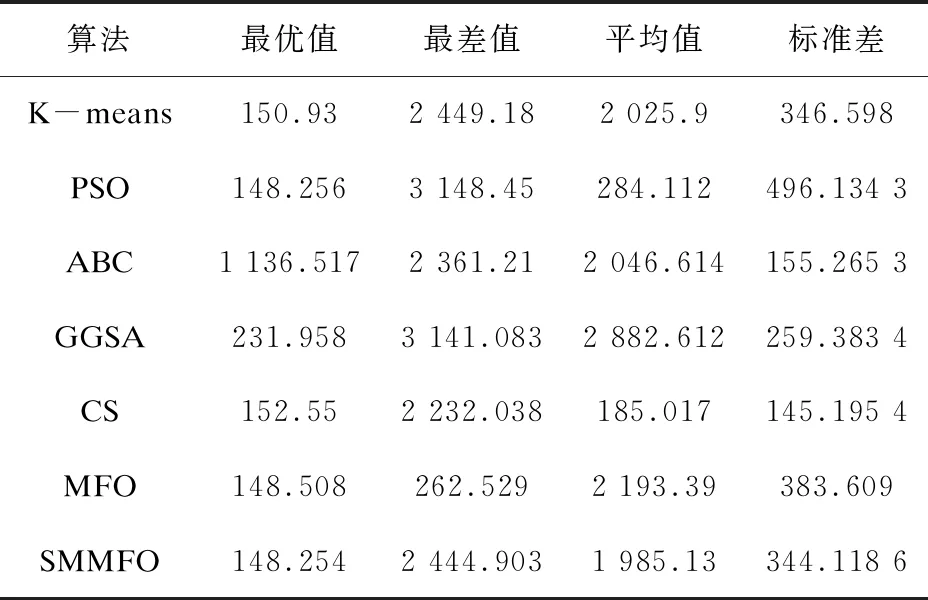
表1 人工数据集1的20次独立运行实验结果

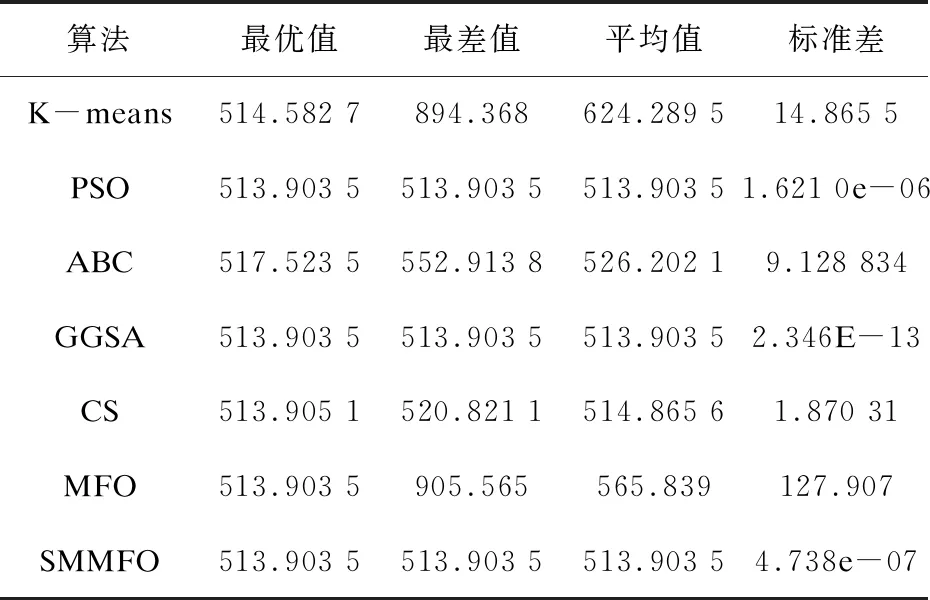
表2 人工数据集2的20次独立运行实验结果

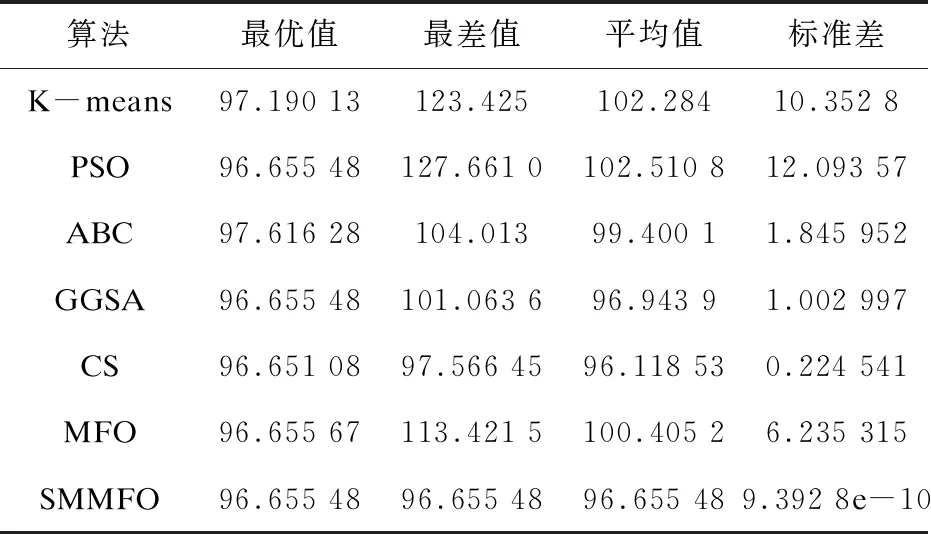
表3 Iris数据集的20次独立运行实验结果

表4 Wine数据集的20次独立运行实验结果

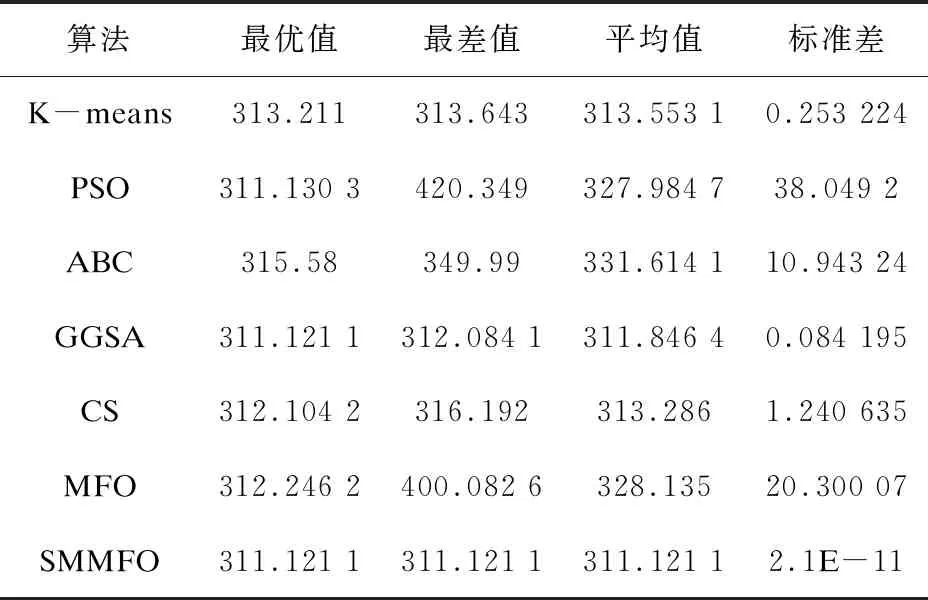
表5 Seeds数据集的20次独立运行实验结果

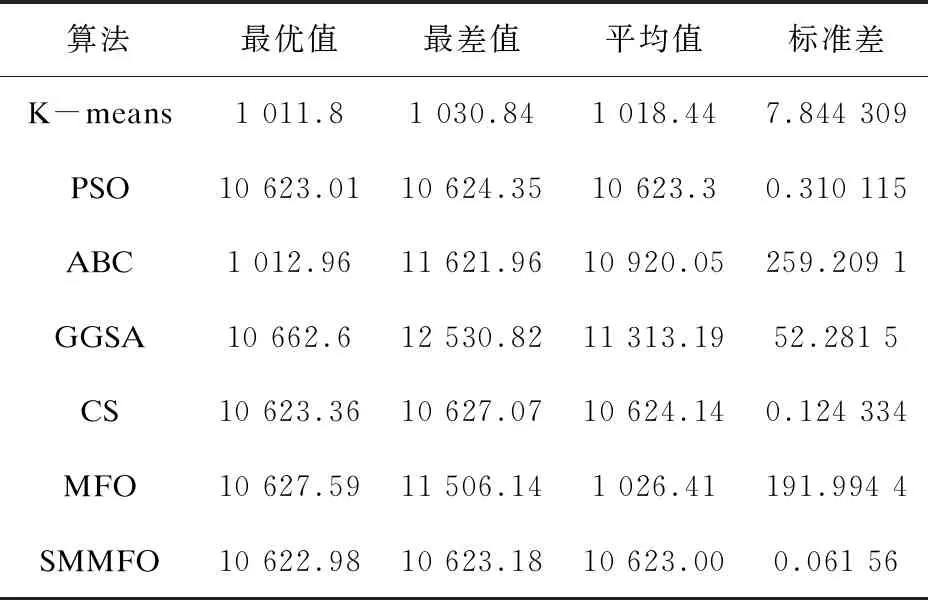
表6 Heart数据集的20次独立运行实验结果

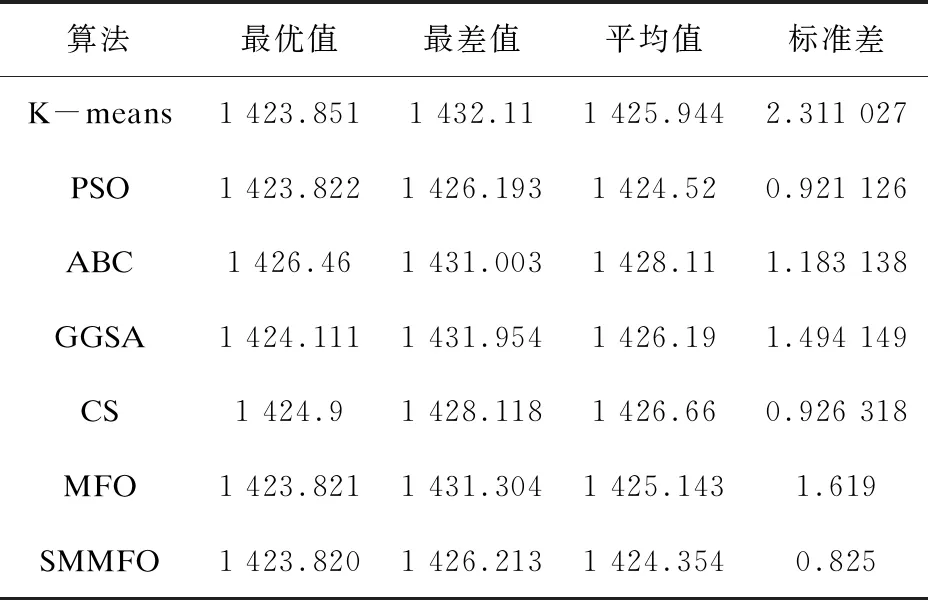
表7 Balance Scale数据集的20次独立运行实验结果

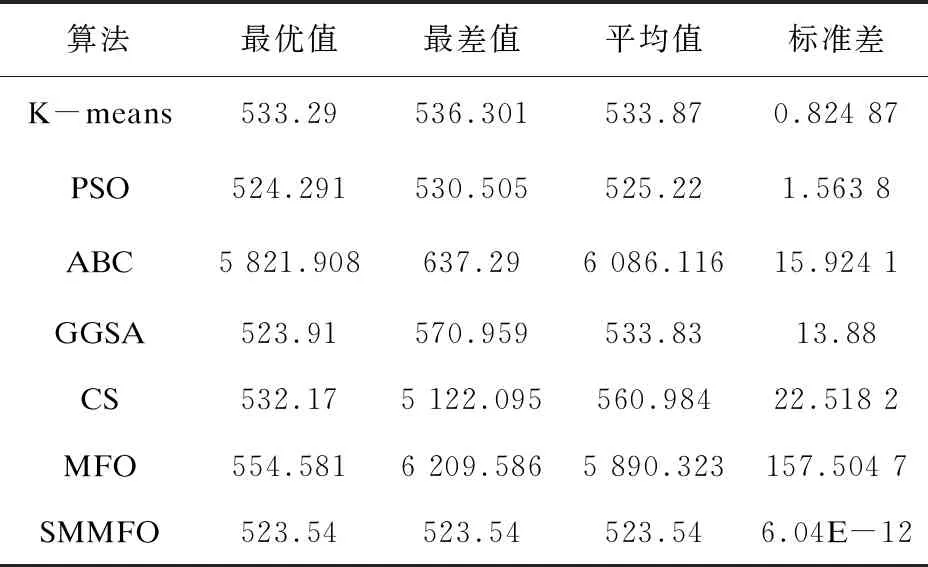
表8 CMC数据集的20次独立运行实验结果

由表1可知，对于人工数据集1，SMMFO所取得的平均值为1 985.13，仅次于CS的185.017，而且SMMFO的最优值是148.254，均优于其他算法。同样在人工数据集2中，SMMFO与PSO，GGSA均取得了513.903 5的较好成绩，而且其标准差也是比较小的。对于Iris测试集，由表3可知SMMFO在最优值、最差值和平均值方面都是96.655 48，而且标准差达到了9.392 8e-10，这表明改进型SMMFO具有较强的鲁棒性，虽然PSO与GGSA给出的最优解也达到了和SMMFO一样的成绩，但是SMMFO在最差值、平均值和标准差方面均优于PSO与GGSA。表4给出了Wine测试集的结果，其中SMMFO取得的最优值、最差值、平均值和标准差分别是16 292.18，16 294.17，16 292.92和0.843 7，这比PSO、ABC、GGSA、CS、MFO和K-means得出的结果都要优秀。对于Seeds测试集，SMMFO的最优值、最差值、平均值均取得了311.121 1这个不错的成绩，而且其标准差为2.1e-11，这是比其他算法都要优秀的，虽然GGSA在最优值方面也取得了311.121 1，但是在其他方面却要比SMMFO逊色很多。对于Heart测试集，SMMFO取得的最优值、最差值和平均值分别为10 622.98，10 623.18，10 623.00，这样的结果比其他算法都要好，在标准差方面，SMMFO的标准差为0.061 56，在这些算法中也是最优秀的。对于Balance Scale测试集，SMMFO所得到的最优值和平均值分别是1 423.820和1 424.354，这两个结果是要优于其他算法的，并且SMMFO取得的标准差也是小于其他算法的。对于测试集Contraceptive Method Choice (CMC)，SMMFO得到的最优值、最差值和平均值均为523.54，这一结果是优于其他算法的，而且其标准差达到了6.04e-12，这个结果更是比其他算法要优秀很多。通过以上数据分析可知，改进型SMMFO算法具有较强的搜索能力，并且在聚类分析方面是具有优势的。

图1是SMMFO算法对人工数据集2的聚类结果，从图中可以看出，新算法取得了比较理想的成绩。

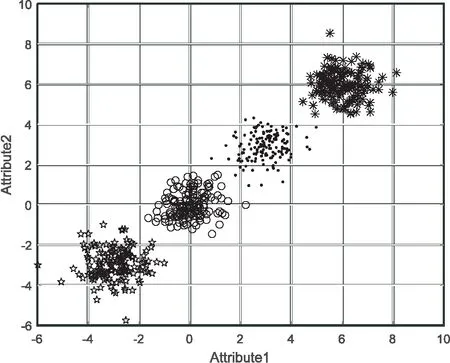
图1 人工数据集2聚类结果

4 结束语

针对飞蛾扑火优化算法容易陷入局部最优及由种群多样性低导致的全局寻优能力不足等缺陷，提出了基于单纯形法的飞蛾扑火优化算法，即在飞蛾扑火优化算法的基础上，加入了一种经典的传统优化方法——单纯形法。改进后的SMMFO算法不仅了提高了种群多样性，而且加强了算法的局部搜索能力，并使其收敛速度大大加快。通过与其他六个算法的对比实验可知，SMMFO不仅在全局搜索方面表现不俗，更是在局部搜索方面表现出了良好的性能，所以，改进型SMMFO是一种非常有效和实用的方法。