带软时间窗的同时取送货车辆路径问题研究
2020-11-15李博威户佐安贾叶子唐诗韵
李博威,户佐安,贾叶子,唐诗韵
(西南交通大学 1. 交通运输与物流学院;2.综合交通大数据应用技术国家工程实验室,四川 成都 611756;3.广西交通设计集团有限公司,广西 南宁 530029)
随着物流与运输行业的蓬勃发展,基本送达服务已无法满足大众需求,而高品质、高效率的配送服务,更为大众所青睐。如何提升配送、运输等方面的效率,是研究者所面临的一道难题。面对多元化的运输需求,传统配送服务在配送时间、客户满意度等方面仍存在较大提升空间。同时,配送人员在配送过程中也会面临需要沿途装载取回货物等情况,对有容量约束的配送车辆来说同样是新的考验。因此,考虑同时满足软时间窗与同时取送货需求的研究是迫切且必要的。而如何保证满足客户需求的同时,降低物流成本,提升运输效率,对提升整个行业服务标准与盈利水平均有较大帮助。
车辆路径问题(vehicle routing problem, VRP)自1959年由Dantzig等[1]提出后得到广泛关注。带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW)也已得到深入研究。自Solomon[2]针对VRPTW给出相对完备的基准算例与求解算法后,此后研究多基于其基准算例进一步展开。而VRP关于同时取送货问题的研究,由Min[3]提出并在后续研究中得到广泛关注。Dethloff[4]进一步将VRPSPD的模型进行完善。后续研究学者将VRP以上2大研究分支逐步结合,提出带时间窗的同时取送货车辆路径问题(VRPSPDTW)。随后根据时间窗的特点,又将研究领域拓展为带软、硬时间窗的同时取送货车辆路径问题(VRPSPDSTW & VRPSPDHTW)2大类,硬时间窗因其严格约束的特点,到达客户点服务的灵活性较差。Wang等[5]针对VRPSPDHTW建立相应模型,并改进Solomon基准算例,运用遗传算法对模型进行验证。王超等[6-9]根据Wang的研究基础,从算法改进角度设计多种启发式算法进行求解,运用Wang所改进算例对算法进行验证,并与Wang所求解进行比对,证明算法改进后,求解效率更高,解的质量更好。石建力等[10]从行驶时间与服务时间随机的角度,考虑更为一般的分批配送情况,研究该情况下集配货一体化车辆路径问题,建立相应模型,同样采用Wang所构建算例,运用改进迭代局部搜索算法验证模型的有效性。户佐安等[11]在考虑客户满意度条件下,构建基于模糊时间窗与货损率的满意度函数,并以客户满意度最大及运输成本最小为优化目标建立相应模型进行求解。而受路况,车况及天气等因素影响,运输过程中存在大量不确定因素,因此软时间窗更符合实际配送情况,对无法在时间窗内准时到达的车辆,满足其在软时间窗外服务总时间最小。目前,针对VRPSPDSTW的相关研究较少,关丽霞[12]、祁文祥等[13]考虑软时间窗下VRPSPD,但其模型中对软时间窗的刻画不够合理。邓爱民等[14]针对带软时间窗的集配货一体化VRP,运用改进模拟退火算法进行求解,但其模型中对车辆使用固定成本与车辆在途前后时间关系上缺乏准确表述。
本文在总结已有研究成果的基础上,进一步改进VRPSPDSTW的模型,对线性约束无法准确刻画车辆起始服务时间与软时间窗关系的问题,考虑引入非线性约束m ax{A,B},结合车辆到达时间在软时间窗内或外的情况,灵活确定车辆起始服务时间,建立能够完整、准确刻画各变量间的关系(包括时间变量在运输全程的前后关系)的模型。
1 VRPSPDSTW的问题描述及数学模型
1.1 问题描述
设路网内有1个配送中心,内设K辆配送车辆;路网内有N个客户点,每一客户点均有不同取送货需求,且各客户点对服务时间有要求,要求服务时间段外进行服务的总时间最小。第k(0≤k≤K)辆车由配送中心始发为各客户点服务,完成服务后须返回配送中心。车辆有容量约束,在全程服务过程中,不允许超出容量限制;且配送中心对车辆返回时间有相应要求,满足所有车辆超出返回时间窗的总时间最小;各客户点有且仅有1辆车进行服务;要求车辆总成本最小。
1.2 模型假设
模型假设条件如下。
1) 路网内仅有1个配送中心,若干客户点,且配送中心及各客户点坐标已知;
2) 车辆全程匀速行驶,且行驶速率为1;
3) 取送货服务的货物品类无差异;
4) 各客户点取送货服务时间相同,不考虑作业不同复杂程度;
5) 各客户点有软时间窗要求,满足所有车辆在软时间窗外服务总时间最小;
6) 车辆由配送中心始发,完成取送服务后,须返回配送中心;
7) 各客户点有且仅有1辆车进行服务,且取送货服务一次性完成,不考虑分批取送;
8) 车辆容量限制。在全程服务过程中,不允许超出容量限制。
1.3 模型变量说明
VRPSPDSTW模型相关变量说明如表1所示。

表1 模型变量说明Table 1 Model variable description
1.4 模型建立
在结合文献[5-9]总结的混合整数规划(mixed integer programming, MIP)模型基础上,对软时间窗约束着重刻画,明确车辆在途前后时间关系,将全程各节点时间关系进行完整表述,构建VRPSPDSTW的混合整数非线性规划(mixed integer nonlinear programming, MINLP)模型。其中,变量集合定义如下。
1) 路网内客户点集V={1,2,···,n};
2) 路网内配送中心与客户点集V0=V∪{0};
3) 车辆集K={1,2,···,m}。
运输全程需针对多个目标进行优化,包括全程车辆行驶路径最短、全程使用车辆数最少、车辆全程违反软时间窗所产生的总等待时间最少、车辆全程违反软时间窗所产生的总迟到时间最少和客户满意度最高5个优化目标。各优化目标的目标函数为
1) 全程车辆行驶路径最短
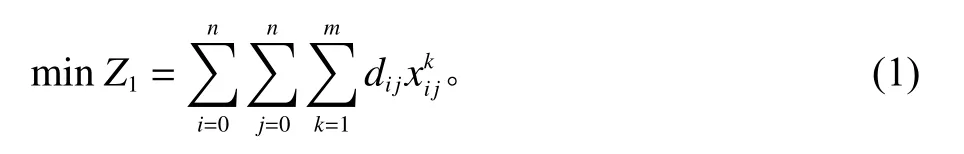
2) 全程使用车辆数最少

3) 车辆全程违反软时间窗所产生的总等待时间最少

4) 车辆全程违反软时间窗所产生的总迟到时间最少

5) 客户满意度以在软时间窗外总违反时间最少来表示,软时间窗外总违反时间越少,说明车辆最大限度满足客户的时间窗要求,因此客户满意度最高。

5个优化目标间相互制约,且存在较为明显的互斥关系,如保证全程使用车辆数最少时,无法同时确保车辆行驶路径最短,或将产生较长行驶距离。对于本文建立的多目标优化模型,为保证全程运输系统最优,考虑采用理想点法进行处理,以各单目标最优值作为其理想值,将多目标条件下,各目标函数值与其理想值间差值的绝对值作为评价函数,满足各评价函数之和最小,将多目标优化转为单目标优化,求出该单目标优化的全局最优解,作为原多目标优化的有效解。转化后的目标函数为


其中,式(7)、(8)确保各客户点仅由1辆车进行取送货,且取送货服务仅进行1次;式(9)为流量守恒方程,确保车辆进入客户点r完成取送货服务后,须驶出并前往其他客户点;式(10)为车辆由配送中心始发,前往各客户点完成取送货服务后,须返回配送中心;式(11)为车辆使用数约束;式(12)为车辆由配送中心始发,前往各客户点进行取送货服务;式(13)为车辆完成取送货服务后,须返回配送中心;式(14)、(15)为车辆从配送中心始发的初始载货量及其约束;式(16)、(17)为车辆返回配送中心的载货量及其约束;式(18)、(19)、(20)为车辆由配送中心前往初始客户点、完成初始客户点后各客户点间及完成客户点取送货服务后返回配送中心的车辆在途载货量关系;式(21)、(22)、(23)为车辆由配送中心前往初始客户点、完成初始客户点后各客户点间及完成客户点取送货服务后返回配送中心的时间关系;式(24)为消除运输网络子回路;式(25)为0 −1变量
2 VRPSPDSTW多目标优化求解算法分析
本文所构建的VRPSPDSTW模型属MINLP,变量类型包含0-1变量与连续变量,约束条件包括线性约束与非线性约束,属NP-Hard类非凸优化问题。针对中小规模的此类优化问题,可考虑采用精确算法进行求解,因此,设计相应求解算法,采用LINGO 17.0对模型进行精确求解,具体求解算法如下图1所示。
3 算例分析
本文采用Wang等[8]改进的Solomon关于VRPTW的经典基准算例对上述模型及算法的有效性进行验证。选取其中5、10个客户点规模的6组算例,其客户点位置生成方式为随机分布和聚类分布混合。
根据以上假设条件及算例数据,合理规划车辆使用与行驶路线,满足评价函数目标值最小。每组算例具体车辆使用与行驶路线如图2和图3所示,各项指标如表2和3所示。
从上述求解结果可知,针对客户点规模为5和10的6组算例,均已找到符合模型的有效解,且满足在单目标优化下取得全局最优,验证了模型及算法的有效性。且无论对时间窗较紧或较为宽松的算例,所建模型均表现出良好的适应性,将违反时间窗的总时间限制在最小限度,进而取得较高的客户满意度(>94%),证明该模型同时具有较强的鲁棒性。通过引入理想点法对目标函数进行重构,平衡了多目标优化中不同尺度目标间的关系,并求得对应问题的全局最优解。

图1 VRPSPDSTW多目标优化求解算法流程图Figure 1 Flow diagram of multi-objective optimization algorithm for VRPSPDSTW

图2 RCdp0501、RCdp0504、RCdp0507车辆行驶路线图Figure 2 Maps of vehicle route for RCdp0501, RCdp0504, RCdp0507

图3 RCdp1001、RCdp1004、RCdp1007车辆行驶路线图Figure 3 Maps of vehicle route for RCdp1001, RCdp1004, RCdp1007
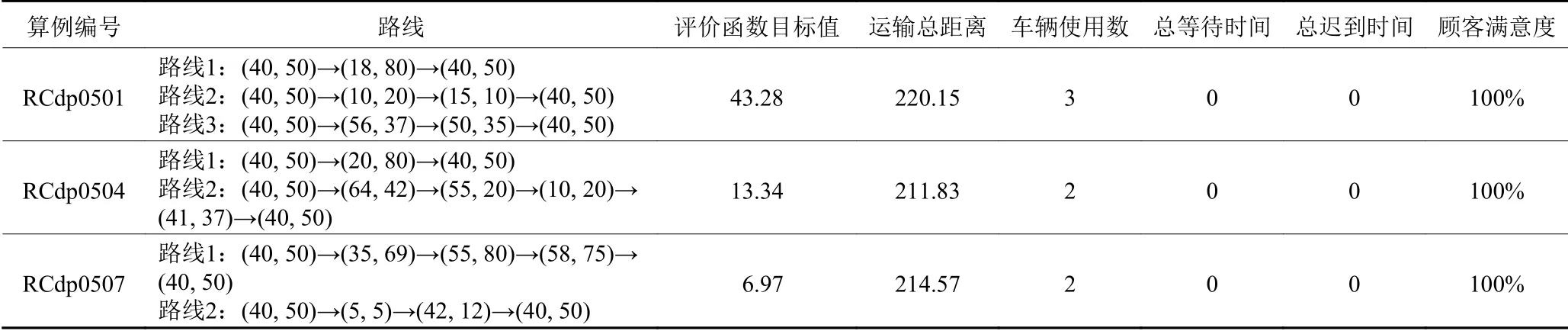
表2 LINGO 17.0针对RCdp0501、RCdp0504、RCdp0507求解结果Table 2 Solving solutions of RCdp0501, RCdp0504, RCdp0507 by LINGO 17.0

表3 LINGO 17.0针对RCdp1001、RCdp1004、RCdp1007求解结果Table 3 Solving solutions of RCdp1001, RCdp1004, RCdp1007 by LINGO 17.0
4 结论
本文针对VRPSPDSTW,构建相应MINLP模型,根据车辆在途过程中,到达不同客户点前后时间关系进行标定,同时对软时间窗表现形式与筛选过程实现准确刻画,并与车辆在途前后时间关系进行融合,将软时间窗条件下,车辆集配货一体化全过程通过数学模型进行完整刻画。通过设计相应多目标优化求解算法,并运用LINGO 17.0全局求解程序,求得6组算例的全局最优解,最大限度满足各客户点对时间窗的要求,确保车辆行驶路径最短与车辆使用数最少,同时获得较高的客户满意度,从而验证了模型及算法的有效性。
此外,本文所研究问题属NP-Hard问题,当客户点数量规模较大时,LINGO的精确算法往往在多项式时间内无法求得全局最优解。因此,对于VRPSPDSTW,今后研究考虑针对问题及模型自身特点,设计相应启发式算法搜索近似最优解,结合大规模算例进行验证,测试算法的求解效率与求解精度。同时,在研究过程中发现,由于软时间窗的特殊性,为满足下一客户点对软时间窗的要求,规避违反软时间窗所产生的不利影响,车辆均在完成服务后在上一客户点有较长停留时间。这虽能满足客户点对软时间窗的要求,但不利于运输企业加速车辆周转,造成运输效率低下、运营成本上升,对企业长期发展产生不利影响。因此,加快路网内车辆周转,缩短车辆在各客户点的停留时间可作为下一步研究方向。
