污染环境中微生物治理种群动力学优化算法*

黄光球，陆秋琴

西安建筑科技大学 管理学院，西安 710055

1 引言

群智能算法是利用一些特殊自然现象开发出来的算法，对复杂优化问题具有很好的适应性。此类算法近几年得到了快速发展。早期的群智能算法所利用的自然现象都很简单，因而这些算法的结构较简单[1-5]等。然而，随着面临的优化问题越来越复杂且维数不断增加，传统的基于简单自然现象的简单结构群智能算法向基于复杂自然现象的复杂结构群智能算法演变是必然趋势。

种群动力学是采用数学方法描述种群个体相互作用关系[6]。由于种群中的个体可以解释为优化问题中的试探解，个体间的相互作用可以映射成试探解的改进，种群的进化活动可以映射成算法的逻辑结构。因此，种群动力学与群智能算法具有天然的联系。

文献[7]采用保护区种群迁移动力学模型构造出了PZPMDO（protected zone-based population migration dynamics optimization）算法，该算法利用保护区与非保护区之间的种群迁移行为构建出进化算子；文献[8]采用捕食-被食动力学模型构造出了OA-PPD（optimization algorithm based on predator-prey dynamics with competition among the same species）算法，该算法的演化算子是基于两种群间的捕食和被食行为而构造出来的；文献[9]利用微生物培养动力学模型构造出了MDO（microbial dynamics optimization）算法，该算法的演化算子是基于微生物种群在营养物质和有害物质作用下的生长特征变化规律而构建出来的；文献[10]利用Lotka-Volterra 生态平衡动力学模型构造出了EBDO（ecological balance dynamics-based optimization）算法，该算法利用生态系统中消费者种群、自养者种群和分解者种群相互间的营养供给关系构造出了演化算子。

水体富营养化是指在人类活动的影响下，氮磷等物质大量进入湖泊、河流、池塘等缓流水体，引起藻类及其他浮游生物迅速繁殖，水体溶解氧量下降、水质恶化、鱼类及其他生物大量死亡的现象[11]。20 世纪70 年代兴起的生物修复技术相比传统技术具有费用低且不会发生二次污染的优点[11]，正在逐步被推广。研究表明，微生物在水体富营养化的治理中可以发挥重要作用[12-15]。

一个池塘中水体的富营养化及其生物治理过程是一个较复杂的自然现象，该复杂自然现象能够被数学模型很好描述。本文基于具微生物治理和基因突变，且种群内部个体之间具有竞争关系的种群动力学模型，提出了一种新的种群动力学优化算法，简称PDO-MCCE（population dynamics optimization algorithm under microbial control in contaminated environment）算法。在该算法中，采用了与现有种群动力学优化算法不同的设计思路，构造出的算子可以充分反映正常种群、突变种群、环境有害物质和微生物种群之间的相互作用关系[9]，该算法适用于求解高维优化问题[9-10，16-19]。

2 算法基本原理

2.1 算法场景设计

假设在一个池塘的水体中生活有一种生物种群，该种群由若干个生物个体组成，这些个体的编号形成的集合为A1={1，2，…，Q1}，该种群称为正常种群A。池塘周围建有若干家化工厂，每隔一段时间，这些化工厂向该池塘的水体中注入含有氮磷的有害污水P，长期下来引发了池塘水体的富营养化，从而造成了该生物种群大量繁殖，进而使得池塘的水质变差。在有害污水的作用下，正常种群A中一些生物个体的基因会发生突变，从而演变出另外一种新种群，称为突变种群B，其中的个体编号形成的集合为A2={1，2，…，Q2}。为了对该池塘的水体生态进行修复，环保部门定期投放一种微生物种群M。正常种群和突变种群，相互之间存在竞争关系，同一种群内部的个体是密度制约的。

正常种群和突变种群中的所有个体均可由n个特征描述，故种群类型u中的个体i可用来表示，其中是种群类型u中的个体i的特征j，i=1～Qu，j=1～n，u=1 表示正常种群，u=2 表示突变种群。

假设所要求解的优化问题为：

式中，F（X）为目标函数；S为解空间；X为n维解向量。在S中任意选择Q1+Q2个试探解，即，其中，i=1～Qu，u=1～2，为解分量；池塘与S相对应，优化问题式（1）的Q1和Q2个试探解分别与Q1个正常种群与Q2个突变种群中的个体一一对应[9-10，16-19]。

在微生物种群M和化工厂排放的有害物质P的共同作用下，正常和突变种群中的个体的生长状态会产生变化，该变化等价于试探解在解空间S中的空间位置变化[9-10，16-19]。

若某个体的目标函数值小，则该个体所处的空间位置较好，该个体适应度好，此类个体称为强壮个体。反之，适应度差的个体称为虚弱个体[9-10，16-19]。种群类型u中的个体i的强壮程度用个体强壮指数（individual physique index，ISI）来表示。强壮个体具有较高ISI值，虚弱个体具有较低的ISI值。种群类型u中的个体i的ISI指数按式（2）计算：

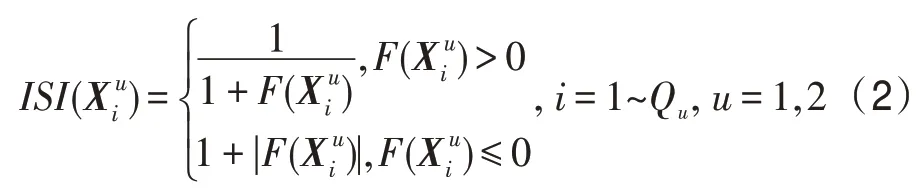
2.2 种群动力学模型

在受到污染的池塘水体中，具微生物治理和基因突变，且种群内部个体之间具有竞争关系的种群动力学模型（population dynamics model with microbial control and gene mutation and competition among individuals in contaminated environment，PDM-MCGMCICE）[11]如下所述：

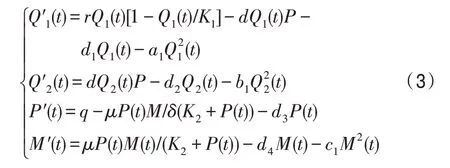
其中，Q1（t）和Q2（t）分别表示正常种群和突变种群中的个体数量；P（t）表示每毫升水体中的污染物的量；M（t）表示每毫升水体中的微生物的量[11]；r为正常种群的增长率，r＞0；K1为环境容量，K1＞0；a1、b1、c1为正常种群和突变种群的竞争系数，则a1，b1，c1＞0；d为由于污染造成的正常种群的突变率，d＞0；d1为正常种群的自然死亡率，d1＞0；d2为突变种群的死亡率，d2＞0；d3是由于其他因素造成的污染物消除率，d3＞0 ；d4为微生物的衰亡率，d4＞0 ；q为污染物单位时间排放量，q＞0 ；μ是微生物生长率[11]，μ＞0；K2为半饱和常数，K2＞0；δ为产出率，δ＞0。为了保证正常种群和微生物种群的正增长，这里假设r＞d1[11]，μ＞d4。

为方便计算，将式（3）改为离散递推形式，即：

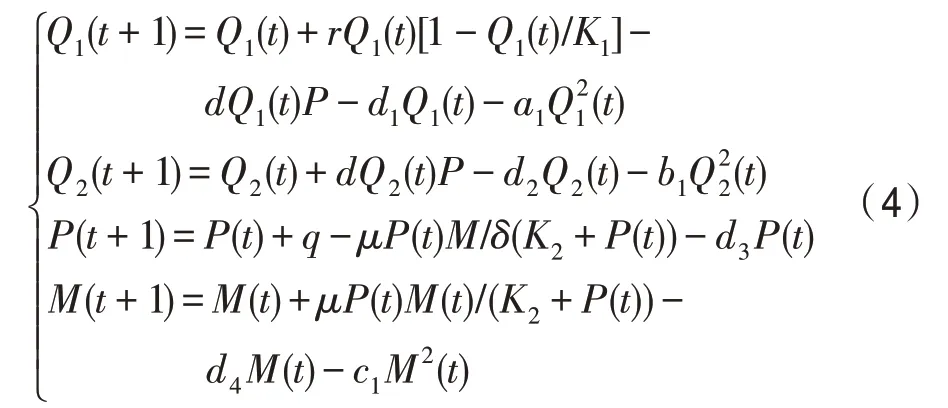
2.3 特征个体集合的选择方法

时期t，对当前种群类型u中个体i来说，其特征个体集合的生成策略如下：

（1）强壮个体集合SPu（t）。从Qu个个体中随机选出ISI 指数比当前个体要高的L个个体，形成集合SPu（t）。L称为特征个体数[9，19]。

（2）普通个体集合GPu（t）。从Qu个个体中随机选出L个个体，形成集合GPu（t）[7-10，16-19]。

（3）虚弱个体集合WPu（t）。将Qu个个体按其ISI指数从小到大进行排列，形成虚弱个体排在前面、强壮个体排在后面的有序集合WPu（t）[9，19]。

2.4 正常和突变个体演化算子设计

PDO-MCCE 算法利用模型式（4）来构造演化算子，从而实现池塘水体中的有害物质P、微生物种群M、正常种群A和突变种群B之间的信息交换，进而实现对优化问题式（1）的求解。

（1）竞争算子。该算子描述的是正常和突变种群内部个体之间的竞争关系。将普通个体集合GPu（t）中种群类型为u的一些个体的某些特征s≠i，传给种群类型为u的个体i，使该个体发生变化：

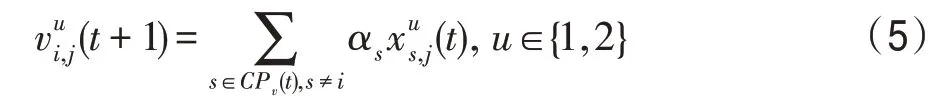
式中，αs=Rnd（-0.6，0.6）；和Rnd（a，b）含义参见文献[19]。

（2）突变算子。该算子描述的是正常种群A中的个体在环境有毒因素P作用下发生基因突变，变成突变种群B中的个体。从正常种群个体集合A1中随机选出一些个体直接发生类型改变，变为突变种群个体：

（3）影响算子。该算子描述的是正常或突变种群内部的一些强壮个体对同一种群内其他个体产生的影响。将种群类型为u的强壮个体集合SPu（t）中一些强壮个体的某些特征，传给种群类型为u的个体i，使该个体受到同类中强壮个体的影响：

式中，βs=Rnd（0.3，0.5）。

（4）毒害算子。毒素算子的含义参加文献[9]。对于种群类型为u的个体i来说，有：

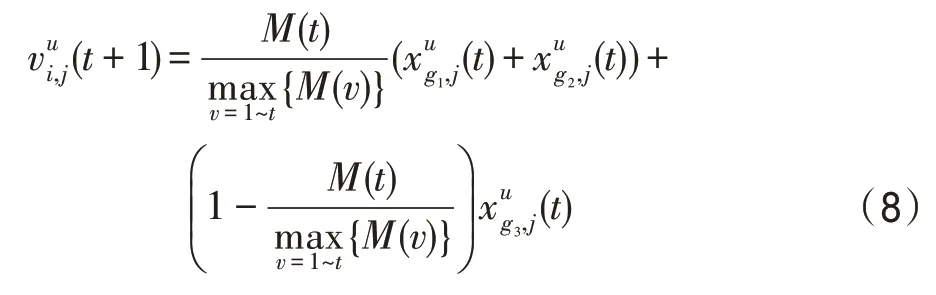
式中，g1，g2，g3∈CPu（t），且g1≠g2≠g3。

（5）新生算子。该算子描述正常和突变种群中个体的新生。从种群类型为u的强壮个体集合SPu（t）和普通个体集合CPu（t）中各随机选择2 个个体进行组合，产生新生个体i：

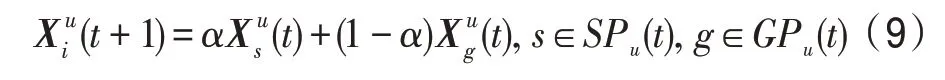
式中，α=Rnd（0.4，0.6）。

（6）死亡算子。该算子描述正常和突变种群中个体的死亡。从种群类型为u的虚弱个体集合WPu（t）选择排在最前面的个体，将其删除。

（7）生长算子[9]。该算子描述的是个体的生长。对种群类型为u的个体i来说，生长算子定义如下：

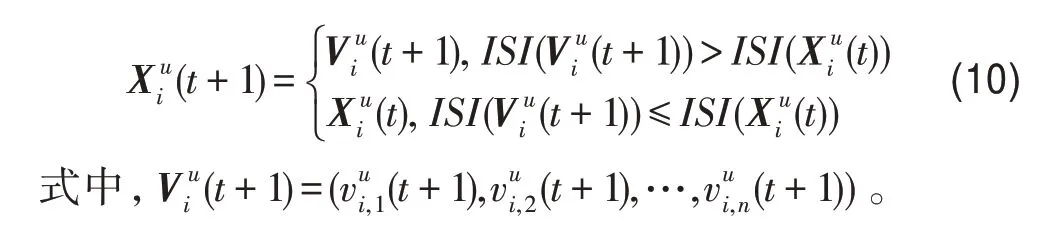
2.5 PDO-MCCE 算法

步骤1初始化：（1）令t=0，设定演化时期数G、计算精度ε、Q1（0）、Q2（0）、个体特征发生变化的最高概率E0、特征个体数L、种群动力学模型参数r、a11、a12、b21、b22、d、d1、d2、d3、d4、q、μ、K1、K2、δ；（2）随机确定、u=1～2、P（0）和M（0） ；（3）从中确定当前全局最优解Y*1。

步骤2执行下列操作：

2.6 算法特征分析

2.6.1 时间复杂度分析

表1 给出了PDO-MCCE 算法的时间复杂度计算过程[9，16，19]。

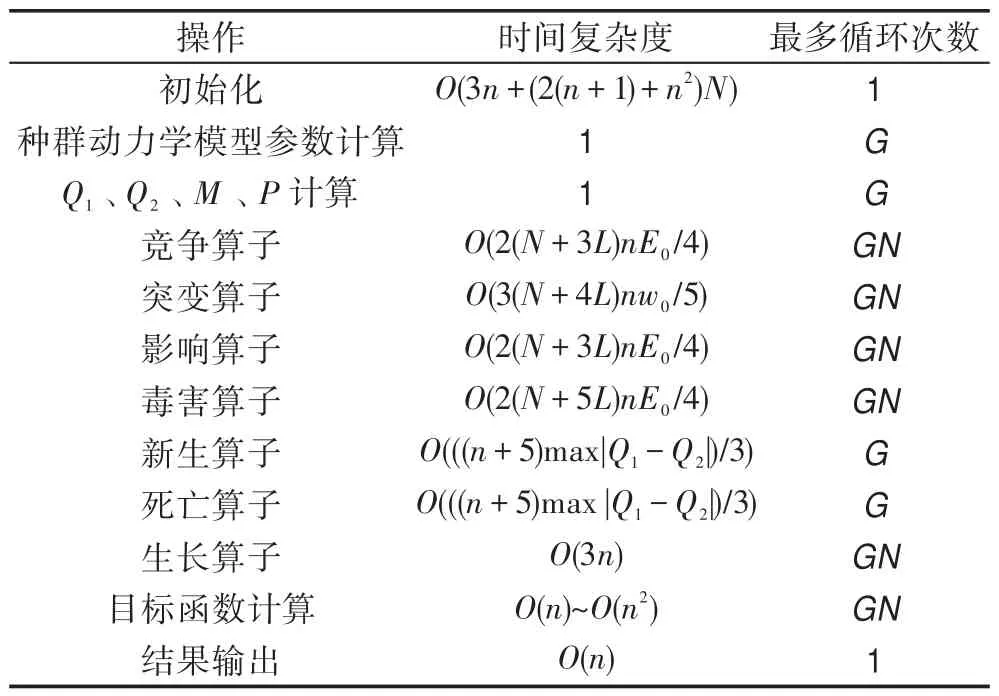
Table 1 Time complexity in PDO-MCCE（N=max（Q1+Q2））表1 PDO-MCCE 算法的时间复杂度（N=max（Q1+Q2））

2.6.2 PDO-MCCE 算法的收敛性分析

（1）Markov 特性。PDO-MCCE 算法的Markov特性分析可参见文献[9，16，19]。

（2）“适应度递增”特性。PDO-MCCE 算法的“适应度递增”特性分析可参见文献[9，16，19]。

（3）全局收敛性。PDO-MCCE 算法的全局收敛性证明可参见文献[16]。

3 参数选择

3.1 PDM-MCGMCICE 模型参数设置方法

文献[11]对式（3）的平衡态的存在性和稳定性进行研究，得出如下结论：

定理1式（3）可能存在如下平衡态[11]：

定理2[11]对于式（3）来说，有：

从定理2 的（4）可知，当（r-d1）（μ-d4）＞dd4K2时，E4（Q1，Q2，P，M）能够达到局部渐近稳定。也就是说，Q1、Q2、P、M的大小能够趋于稳定。

由2.6.2 小节可知，PDO-MCCE 算法进行全局最优解搜索时，搜索过程具有Markov 特性。因此，搜索过程的Markov 随机性保持得越持久，越不易陷入局部最优解陷阱。因此，PDM-MCGMCICE 模型参数r、a1、b1、c1、d、d1、d2、d3、d4、q、μ、K1、K2、δ的确定在满足定理1 的第（4）条要求的同时，应保留足够的随机变化特性。

综上所述，PDM-MCGMCICE 模型参数选择只要按定理1的第（4）条的要求选取，就可使PDO-MCCE算法的搜索过程不易陷入局部最优解陷阱。

经过仔细筛选，可取r=Rnd（0.63，0.77），q=Rnd（9，11），μ=Rnd（0.135，0.165），d=Rnd（0.013 5，0.016 5），d1=Rnd（0.117，0.143），d2=Rnd（0.009，0.011），d3=Rnd（0.135，0.165），d4=Rnd（0.045，0.055），K1=Rnd（180，220），K2=Rnd（0.18，0.22），δ=Rnd（3.6，4.4），a1=0.000 1，b1=0.01，c1=0.000 1。此时，Q1=161.86，Q2=56.65，P=0.1，M=798.8。

应用上述取值策略，Q1、Q2、P、M的初始值分别设为100、50、5、200 时，利用式（3）可以计算出Q1、Q2、P、M随时间的变化情况，如图1 所示。从图1可知，Q1、Q2、P、M具有极好的随机性，且Q2还具有周期性突跳特征，有利于使搜索进程跳出局部最优解陷阱。

3.2 算法运行控制参数设置方法

（1）不要精确设置的参数G和ε。这两个参数可按文献[16]介绍的方法选取。

（2）关键参数E0、L。这两个参数对算法性能影响较大，需要对其特性进行研究。

Bump 优化问题是一个极难求解的有约束优化问题，其特征与工程优化问题很相似，经常用来探明群智能算法的参数性能[16]。故本文以Bump 优化问题为例来探明E0、L的取值规律。Bump优化问题如下：

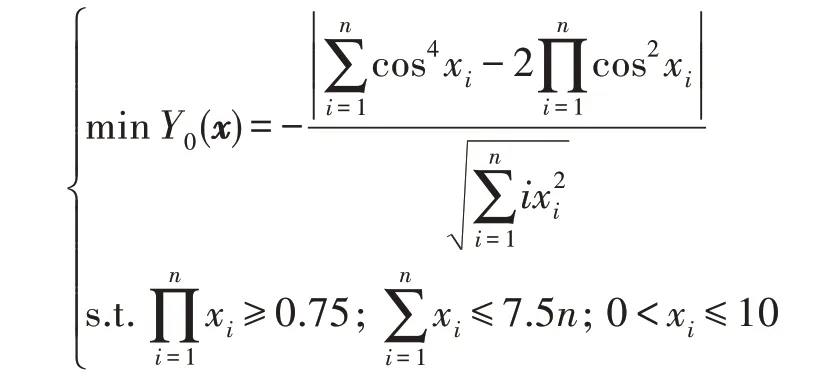
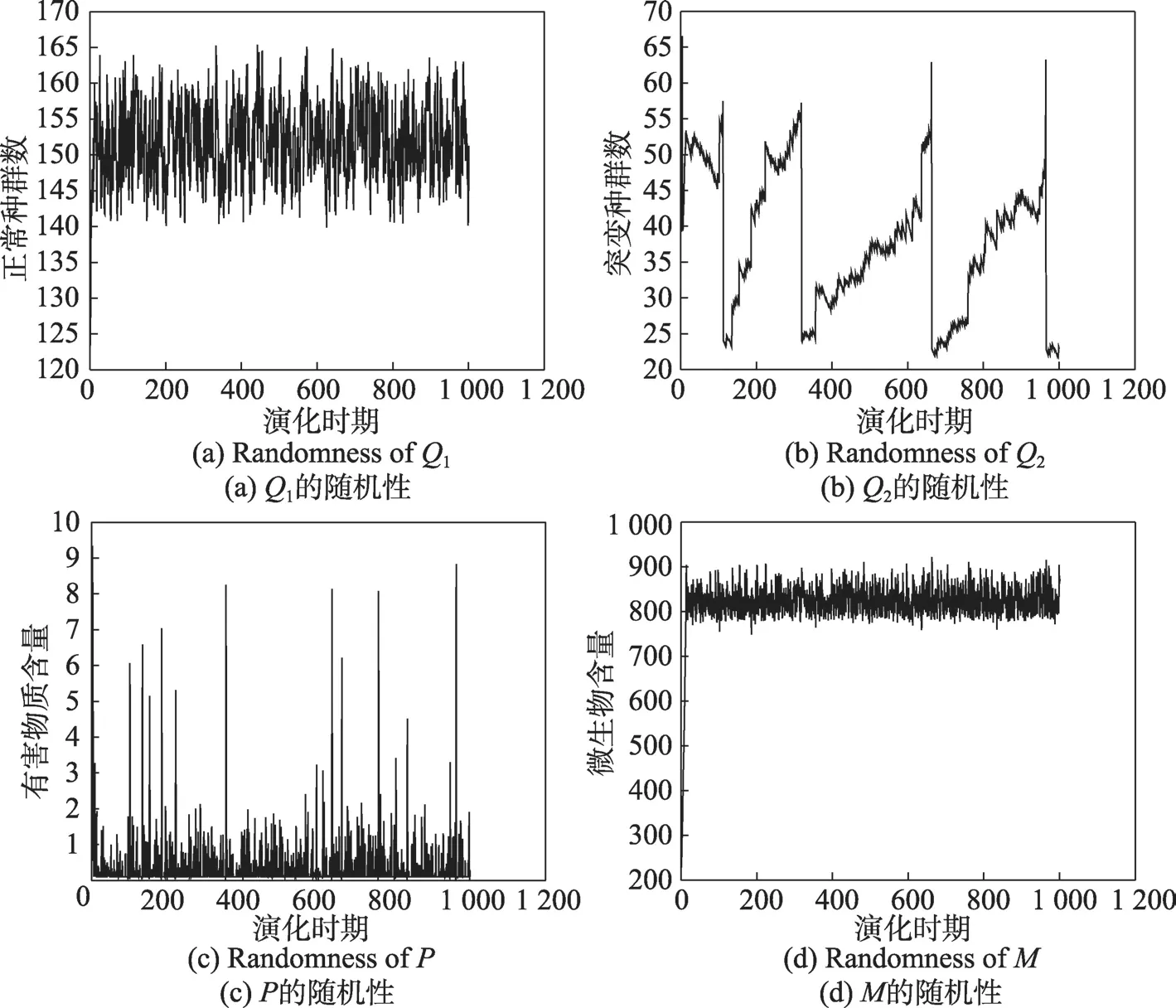
Fig.1 Randomness of Q1、Q2、P、M图1 Q1、Q2、P、M 的随机性

表2 描述了当L取不同值时，PDO-MCCE 算法求解Bump 优化问题所获得的结果，计算参数为n=50，E0=0.01，G=108，运行50 次[9，16，19]。从表2 可知，L=3～7 为L的最佳取值区间[9，16，19]。

Table 2 Relationship of L with meanO and meanT表2 L 与meanO 和meanT 之间的关系

表3 描述了当E0取不同值时，PDO-MCCE 算法求解BUMP 优化问题所获得的结果，计算参数为n=50，L=3，G=108，运行50 次[9，16，19]。从表3 可知，E0=0.006～0.100 为E0的最佳取值区间[9，16，19]。

Table 3 Relationship of E0 with meanO and meanT表3 E0 与meanO 和meanT 之间的关系

4 与其他算法比较

CEC2013[20]是国际上通用智能优化算法测试包，其中包括有28 个非常复杂的函数优化问题[9，16，19]，这些优化问题共分3 类，每类函数优化问题的特性可参见文献[9，16，19]。本文在第1 类即单峰函数类选用F2 和F3，在第2 类即多峰函数类选用F15 和F19，在第3 类即组合函数类选用F21、F22 来测试PDOMCCE 算法的性能。

本文用PDO-MCCE算法去求解F2、F3、F15、F19、F21 和F22，其参数是n=50，G=108，ε=10-7，E0=0.01，L=3[9，16，19]。与PDO-MCCE算法进行比较的7 个智能优化算法均选自国际著名期刊近期刊登的知名算法[9]，这些算法是ABC（artificial bee colony）[3]、MpBBO（metropolis biogeography-based optimization）[4]、NP-PSO（non-parametric particle swarm optimization）[5]、RCGA（real-coded genetic algorithm）[21]、DASA（differential ant-stigmergy algorithm）[22]、Copt-aiNet（artificial immune net applied to distribution system reconfiguration with variable demand）[23]、SLADE（differential evolution with self-adaptive strategy and control parameters based on symmetric Latin hypercube design）[24]，这些算法的参数设置可参见相关文献。这7 个算法的终止运行条件为：进化代数G=108或者最优解误差ε=10-7[9，16，19]。

针对每个函数优化问题，每个参与比较的算法分别独立运行51 次，以寻找全局最优目标函数[9-10，16，18-19]。表4 给出了每个算法所求得的最优目标函数值的平均值（Average）、中值（Median）、标准差（STD）、适应度评价次数（FE）、最优目标函数值的最小值（Min）与最大值（Max）[9-10，16，18-19]。8 个算法求解每个函数优化问题的性能排名Rank1 是基于Average 的精度进行的排名，Rank2 是基于Average 的精度和FE 进行的排名；Rank1 最终排名和Rank2 最终排名是分别基于Rank1 和Rank2 排名总积分而进行的排名。

从表4 可以看出这8 个参与比较的算法按Rank1和Rank2 的性能排序如下：

图2（a）～（f）说明了各算法求解每个优化问题时的样本收敛曲线。从表4 可知，PDO-MCCE 算法均能获得理论全局最优解或以很高的精度发现全局最优解。

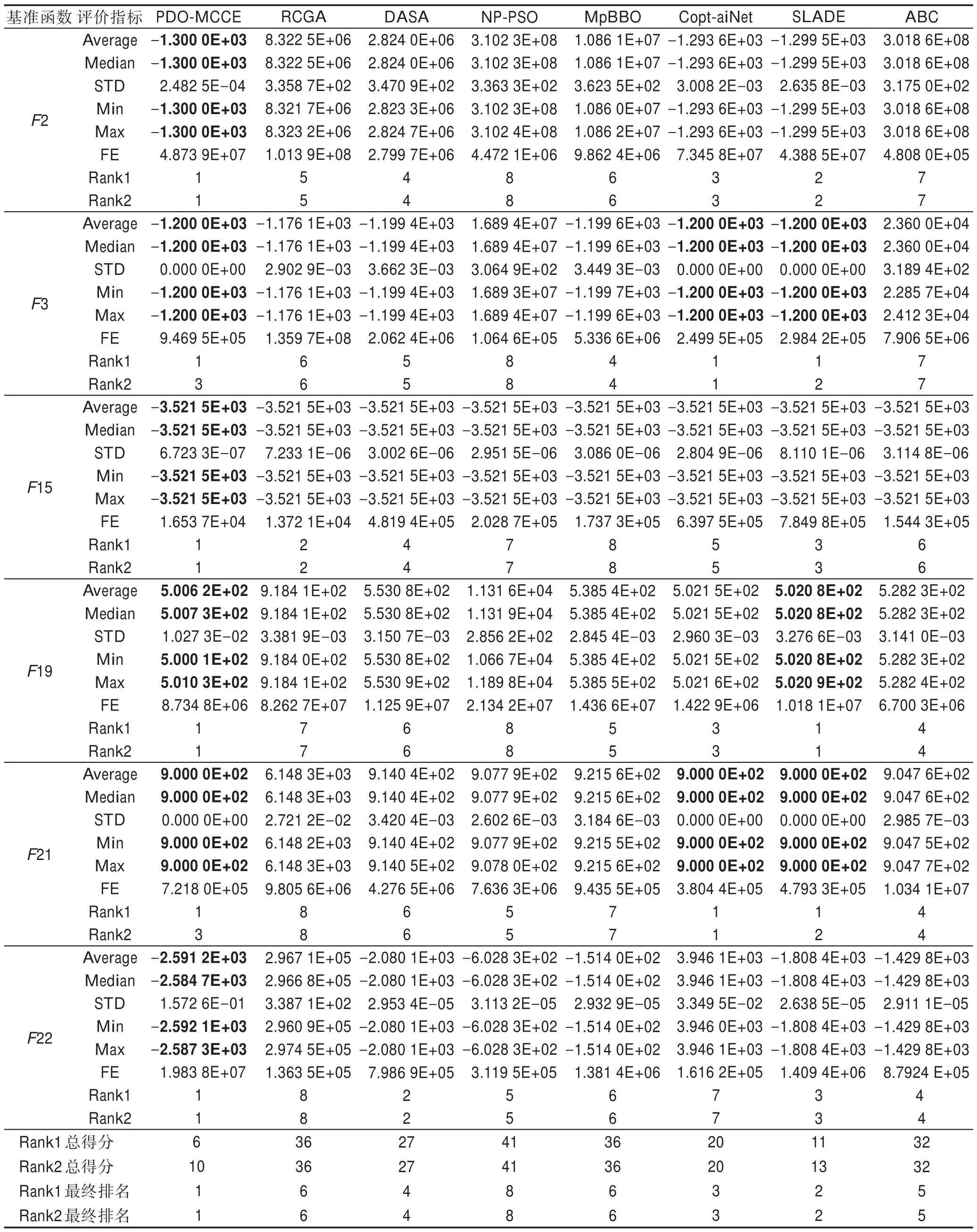
Table 4 Results of comparison calculation表4 对比计算结果

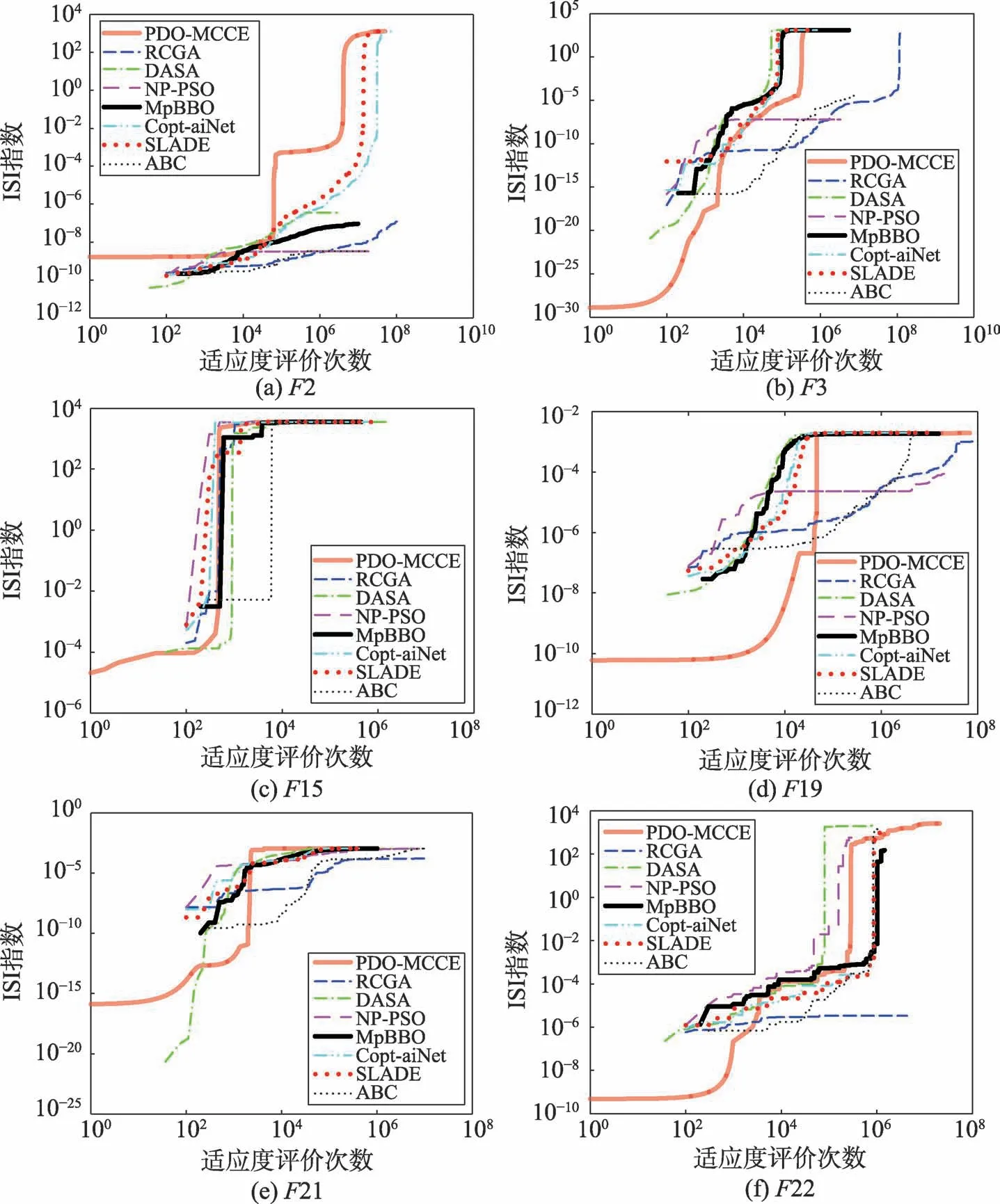
Fig.2 Convergence curves图2 收敛曲线

5 求精、探索及其平衡性分析

（1）求精能力分析。从图2（a）～（f）知，与7 个被比较算法相比，PDO-MCCE 算法的收敛曲线在一些时间段内上升较慢且持续时间长，表明该算法提升最优解精度的过程十分明确。该特征说明PDOMCCE 算法的求精能力比7 个被比较算法强[7-10，16-19]；从表4 知，PDO-MCCE 算法求解F2、F3、F15、F19、F21、F22 时，均能获得其理论全局最优解，此说明PDO-MCCE 算法比7 个被比较算法具有更好的求精能力[7-10，16-19]。

（2）探索能力分析。从图2（a）～（f）知，与7 个被比较算法相比，PDO-MCCE 算法的收敛曲线在一些时间段内较陡且持续时间短，表明该算法提升ISI 指数的耗时很短。该特征说明PDO-MCCE 算法比7 个被比较算法具有更好的探索新空间的能力[7-10，16-19]。

（3）求精和探索能力的平衡性分析。从图2（a）～（f）可知，与7 个被比较算法相比，PDO-MCCE 算法的缓（求精能力）和陡（探索能力）交替出现，且缓的持续时间均较长，陡的持续时间均较短，此表明PDOMCCE 算法的求精和探索能力的平衡性均优于7 个被比较算法[7-10，16-19]。

6 结束语

本文基于PDM-MCGMCICE 模型提出了一种具有全局收敛性的新型优化算法，与其他典型群智能算法相比，PDO-MCCE 算法具有如下特点：

（1）个体被自动划分成2 类，每类个体数依据PDM-MCGMCICE 模型自动进行调整，增加了个体的多样性，解决了人为确定个体数的难题。

（2）所有算子是通过利用PDM-MCGMCICE 模型以及种群间和种群内的个体间的相互作用关系来进行构造的，不需要与要求解的实际优化问题相关。因此，PDO-MCCE 算法具有很好的普适性[7-10，16-19]。

（3）PDO-MCCE 算法中的每个算子具有明确功能，其中竞争算子和突变算子分别可实现种群内和种群间个体的信息交换；而影响算子可实现种群内强壮个体的信息扩散[7-10，16-19]；毒害算子可将环境信息传递给不同种群内的个体，使其受到环境的影响；新生算子可增加强壮个体数；死亡算子可以减少虚弱个体数；生长算子可确保算法具有全局收敛性。

（4）突变种群内的个体数的周期性突然增加，有利于大量强壮个体突然参与搜索，从而可大幅增加搜索进程跳出局部最优解陷阱的概率。

（5）采用PDM-MCGMCICE 模型的机理确定PDO-MCCE 算法中的相关参数，大幅减少了该算法参数的人工确定个数。实际上，PDO-MCCE 算法需要人工确定的参数只有2 个。

（6）由于每个时期只有3/500～1/10 的个体特征参与计算，导致PDO-MCCE 算法的时间复杂度大幅降低，因此该算法适于求解高维复杂优化问题。

PDO-MCCE算法未来需要深入研究的问题如下：

（1）深入研究各算子的动态特征；

（2）深入研究各种群的动态特征。