流体的旋涡特征提取方法综述

2020-11-13邵绪强刘艺林林丽娜

图学学报 2020年5期

邵绪强，刘艺林，杨艳，林丽娜

(1. 华北电力大学控制与计算机工程学院，河北保定 071003；2. 海军装备部装备项目管理中心，北京 100071)

向量场数据可视化大多来自于对流场的模拟和观察，在大部分情形下，向量场数据可看为流场数据[1]。

本文综述从庞大的流体数据集中提取形成特征所需的流体信息的过程，即流体的特征提取过程。这些流体特征是对数据的抽象，通过只提取特征、从面向问题的角度进行数据缩减[2]，从而将可视化提升到更高的抽象级别[3]。该方法经过较为复杂的提取特征，后续的可视化步骤将会较快地实现[4]。随着计算机性能的不断提高，基于特征和拓扑提取的流体可视化技术成为了新的研究热点[5]。

流体特征可视化在医学上应用广泛。在四维核磁共振成像的心脏血流方面，KÖHLER等[6]发现部分疾病的严重程度与血流的某些特性(如涡流核心的位置、旋涡形状和初始位置)有关，并用λ2方法定义旋涡，且提取主动脉中的旋涡核心。实验中涡核呈球体，其半径与旋涡强度成正比。文献中通过使用四维PC-MRI采集技术实现可靠、实时的血流测量，从而对患者进行血流动力学定性和定量分析。目前，医学研究人员正在研究旋涡等特征的流动模式与不同病理的关系提取；在脑动脉瘤风险评估中，OELTZE-JAFRA等[7]发现血流中的旋涡与动脉瘤破裂相关，通过提取涡核线来准确绘制旋涡的观测结果，在涡核线上标注箭头以示血流运动方向。

流体特征可视化在海洋、天气、宇宙等研究领域也受到极大重视。CHELTON等[8]以旋涡的形式对10年来全球海洋的海面高度场进行了分析，并用Okubo-Weiss准则定义旋涡，将旋涡分为气旋型和反气旋型旋涡。由于噪声和阈值的原因，无法识别弱涡；1983年，LUGT[9]在大气中寻找飓风，将物质颗粒围绕一个共同中心的旋转运动定义为旋涡；MARKOWSKI等[10]定义风暴相对螺旋度(storm relative helicity, SRH)，发现其在时间和空间上均为高度可变的，并提出该参数用于预测风暴方面时存在的缺陷；HADJIGHASEM和HALLER[11]提供了一种参考系不变性方法，从非定常流场中提取动态拉格朗日相干结构，并对木星及其他行星大气中的旋涡边界进行探测。

流体的特征提取为特征可视化的首要步骤[1]，本文主要综述流体中旋涡特征提取方法。旋涡的非正式定义反映了人的主观直觉[12-13]，但至今仍很难正式给出旋涡的正式定义[14-16]，因此文献中旋涡提取的依据各不相同。目前，常用的流体旋涡特征提取大致分为基于点、线、几何曲线和基于机器学习的方法。

(1) 基于点的方法。基于样本点处的物理量进行计算，如根据压力[17]或螺旋度[18]等物理量来提取旋涡，其特征通常是流体中的一个连通区域。该方法的缺陷，如难以区分较为集中的旋涡，大多数方法需要设置阈值，微小特征漏判等。近年来提出的Ω方法[19]对阈值和实验效果方面有突破性进展。

(2) 基于线的方法。通过搜索涡核线(粒子做旋转运动所围绕的线)进而提取旋涡，其共性问题是涡核线通常会被过度分割，导致实验效果降低。

(3) 基于几何曲线的方法。通过流线或迹线的几何特性进行旋涡提取，其中曲率中心法和缠绕角度法，分别通过曲率趋于一点和角度累计达到2π等条件来提取旋涡区域。该方法时间复杂度较高，在三维空间的应用仍需一定的改进。

(4) 基于机器学习的方法。通过预先训练模型等方法有效提高了旋涡提取的精度，使用卷积神经网络(convolutional neural network, CNN)等方法提取流场中的旋涡，对传统方法假阳性、假阴性、时间复杂度较高等缺陷均有一定的改进。

根据参考坐标系的运动类型可以将旋涡提取方法分为伽利略不变性、旋转不变性和拉格朗日不变性。目前最理想的方法为拉格朗日不变性坐标系下的旋涡提取，但提取效果提升的同时也存在一些问题，如数据计算量过于庞大等。

与旋涡提取领域其他综述性文章相比，本文除了阐述经典方法外还着重介绍了近几年来的新型旋涡提取方法，如Ω准则、Rortex法、基于机器学习的方法等，让研究者对其研究发展也有一定的深入了解。表1对常用的方法进行总结。

表1 常用的旋涡提取方法汇总Table 1 Summary of commonly used vortex extraction methods

1 相关概念及旋涡提取方法

1.1 流线

流场中，每个点均与速度矢量相切的光滑曲线称为流线。在描述流场时，可用流线簇的疏密程度表示矢量的大小。定常流中流线的位置和形状不随时间变化，即流线式为

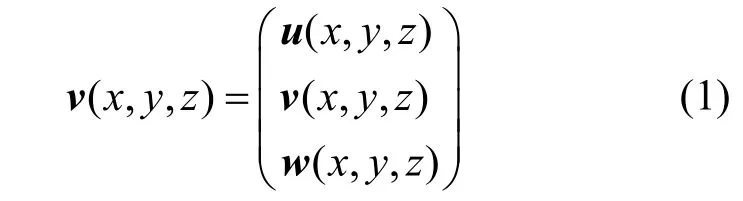
其中，u，v，w为各方向的分量。

SALZBRUNN和SCHEUERMANN[20]提出流线谓词概念，通过为每条流线设置一组谓词定义流结构，从而揭示三维流场中的旋涡问题。ROBINSON等[39]认为，若瞬时流线在垂直于涡核线平面上的投影大致呈圆形或螺旋状，且该投影图形与涡核线有相同的运动趋势时提取到旋涡。在特征可视化研究初期，该方法及其简单的特性被广泛应用，但因自我引用，想找到旋涡需预先计算出涡核线的位置，因此这种方法现实意义较小[40]。CHEN等[41]提出一种将向量场中的周期轨道和分离线作为初始流线的新方法。BANKS和SINGER[42]使用涡度场流线，根据垂直于涡核的平面内的压力最小值进行旋涡提取。GARTH等[43]将流线拓展到流面，提出流面计算和确定涡核边界的新方法，在流体进行复杂运动时该方法也可以获得精确结果。由于流场中存在大量流线，流线方法经常出现漏选情况，ZHENG等[44]根据流线的几何特征来判断其类型并进行分类，该方法能有效筛选多余流线，提高可读性。

1.2 迹线

流场中，流体粒子运动时描绘的轨迹曲线称为迹线。在定常流中，迹线等同于流线；在非定常流中，与流线不同，迹线的位置和形状随时间变化。在此需要区分流线和迹线的性质，流线由同一时间步长下的各个流体质点组成，迹线由同一流体质点在不同时间步长下的位置组成。

大多数情况下，非定常流比定常流更接近自然现象，但是非定常流的计算复杂度较大。随着计算机性能的不断提高，人们也逐渐开始研究非定常流中的旋涡提取。

迹线可表示为

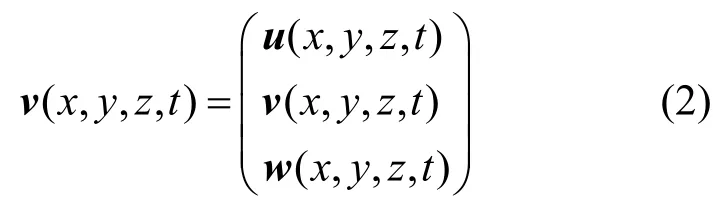
WEINKAUF等[28]将Sujudi&Haimes法[27]推广到迹线，加入时间维度后，迹线表示为

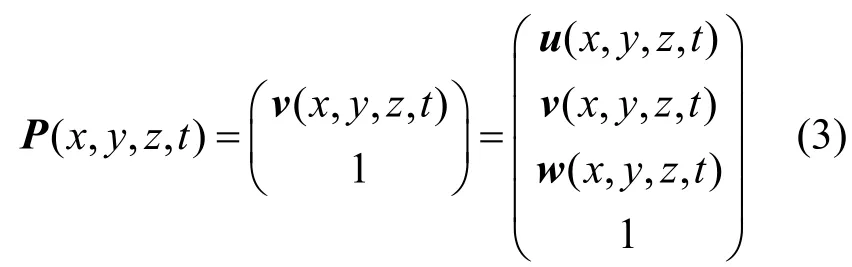
根据非定常流中迹线的特征提取旋涡。

类似于流线谓词，SALZBRUNN等[21]将迹线分为受旋涡影响的迹线和其余迹线2部分。文献[21]定义了基于迹线谓词的框架，根据迹线是否具有特定的属性为每个迹线设置布尔值，因此每个谓词可以将迹线分为两类；结合布尔代数可以将迹线进行更精确的分类，从而对不同的迹线结构进行更精确的定义。

1.3 平行向量场

PEIKERT和ROTH[22]在1999年引入平行向量场的概念，通过设定约束C=V×W=0找出2个向量场V和W平行的点的位置，该方法相当于求出V和W叉积运算的零等值面。在二维中，返回孤立点；在三维中，返回涡核线，如图1所示。

图1 三维中的平行向量场[30]Fig. 1 Parallel vector field in three-dimensional[30]

平行向量场的提出为旋涡提取领域提供了更简洁的方法，可以对大多数旋涡提取方法重新定义并简化计算步骤。PEIKERT和ROTH[22]通过计算v||(∇v)v找到局部曲率为零的点。其中，v为速度；∇v为速度梯度；SCHINDLER等[30]计算平行向量场找出涡核线种子点。

ROTH和PEIKERT[29]提出了一种使用平行向量提取涡核线的方法，利用对速度矢量v进行二阶导数计算，即

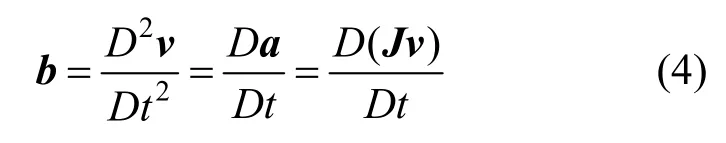
可实现对弯曲旋涡的定位。

1.4 矢量场拓扑

矢量场拓扑[45-47]由临界点和由临界点发出或指向临界点的积分曲线构成，用于清晰明了地表示场信息。1989年，HELMAN和HESSELINK[47]将矢量场拓扑方法用于可视化领域，并将临界点定义为矢量大小为零的点，通过计算雅可比矩阵特征值判断临界点的类型：2个特征值实部为正对应排斥状，和负对应吸引状，一正一负对应鞍状；特征值具有虚部对应旋涡状，实部的正负对应旋出和旋入，实部为零时旋转曲线近似闭合。如图2所示。

图2 矢量场拓扑分类图[47]Fig. 2 Topological classification of vector field[47]

KASTEN等[23]利用矢量场拓扑设计一种鲁棒的旋涡边界提取算法，根据局部加速度最小找到临界点。由于加速度为伽利略不变量，适用于较多文献的实验场景，但是仍高度依赖参考坐标系。MAHROUS等[48]提出了一种基于Sperner定理的涡核区域提取方法，该方法观察每个网格单元边界处的向量，以此分析向量场。速度矢量在旋涡附近表现出特定的形式，通过搜索这些形式找到旋涡。BUJACK等[49]在矢量场中建立局部参考系，同一时间步长下在流场不同区域中使用不同的坐标系，根据雅可比矩阵行列式极值提取临界点。在三维中，矢量场拓扑仍有很好的实用性，HELMAN和HESSELINK[50]证明当存在2个复特征值时，总会存在一个对应的实特征值，由此可在三维空间中得到焦点或中心点，从而提取旋涡。

1.5 旋涡新定义——旋涡矢量(Rortex)

由于至今仍没有给出旋涡的明确定义，导致研究人员在各自的旋涡提取方法中的判断依据各不相同，为初学者造成理解的混乱。

LUGT[9]对旋涡定义是：许多粒子围绕一个共同的中心旋转的运动。尽管其与视觉上的直接观测结果表述类似，但不适于设计旋涡提取算法。

目前大多数旋涡提取方法将速度梯度张量(雅可比矩阵)的特征值作为判断条件。这些基于特征值的方法存在几个不可避免的问题，如旋转轴的识别过程性能较差，存在剪切力的影响等。为了解决以上问题，从数学的角度出现了一个基于特征向量的矢量，称为旋涡矢量[51]，其大小与垂直于旋转轴平面中的旋转强度有关，方向由速度梯度矩阵的实特征向量确定，表示旋涡的旋转轴。根据旋涡矢量的定义，将旋涡定义为旋涡矢量为正数的流通区域。

由于该方法并非基于流体动力学，因此无论是不可压缩还是可压缩流体，旋涡矢量均可以准确地提取旋涡。该方法还有另一优点，Rortex法中的旋涡矢量可以同时表示旋涡的旋转强度和旋转方向，这是众多标量方法无法做到的。

文中提出的快速计算Rortex算法可以准确地描述局部流体的旋转，能清晰地显示旋涡结构。TIAN等[52]对算法进行优化后，Rortex算法与λ2准则的计算时间大致相同。在后期研究中，GAO和LIU[24]发现剪切力对复特征值的虚部有一定的影响，而基于Rortex的方法可以进行准确测量。

2 流体旋涡特征提取传统方法分类

2.1 基于点的方法

2.1.1 基于局部物理量满足阈值要求提取旋涡

该类方法中，阈值的取值极大地影响了实验效果。在早期研究中，HUNT等[17]在定常无粘性的二维流体中定义旋涡区、汇合区和流动区。通过局部压力最小值提取旋涡区域，设置约束P≤Pthresh来找到满足条件的区域，其中，Pthresh为人为设置的阈值，并将该低压区域定义为旋涡区。

后期研究证明局部压力最小不能保证存在旋涡，反之亦然，流体其他的特性也有可能引起旋涡，如螺旋度、涡度等，因此目前一般不采用压力法进行旋涡提取，但其为旋涡提取领域提供了一个良好的开端。

螺旋度一般由速度、涡度等物理量计算[53-54]。该方法通过局部区域螺旋度达到局部区域绝对值最大值来提取旋涡。LEVY等[18]将螺旋度密度Hd、螺旋度H和单位化螺旋度Hn应用于旋涡提取中，即

其中，ω为涡度。

由式(5)可知，螺旋度密度的符号由速度矢量和涡量矢量夹角余弦的符号决定，螺旋度密度较大则表示速度和涡度之间的夹角较小。通过单位化螺旋度在最小曲率流线上达到局部区域绝对值最大值来确定涡核区域位置，由时间上反向积分找到奇异点(速度为零的点)来确定旋涡开始位置，积分得到的曲线即旋涡旋转轴。该方法解决了由低涡度流场区域，以及速度矢量和涡度之间的角度较大(如边界层)的高涡度低速区域引起的误判问题。

螺旋度法的一个优点是螺旋度归一化到[-1,1]的范围，用于确定涡轴方向。但是该方法无参考系不变性，因此其只能应用于定常流或固定某一帧的旋涡提取。且该方法不考虑某些特殊情况，如Hn分母为0等。

2.1.2 基于速度梯度提取旋涡

涡度作为一个伽利略不变量，与流体粒子的角速度有关，然而涡度不能区分纯剪切运动与旋涡的实际旋转运动，因此不适合用作旋涡提取。目前基于对速度梯度∇v=Ω+S及其对称部分Ω和反对称部分S的一类方法应用广泛。该类方法采用由HUNT[25]提出Q准则。ZHOU等[55]提出

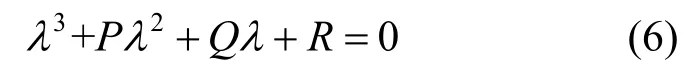
得出P，Q，R的关系。其中，P，Q，R由速度梯度∇v

导出。其中，tr为矩阵的迹；det为行列式的绝对值，且

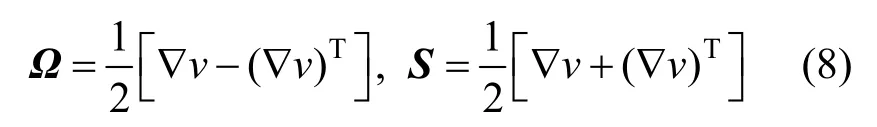
其中，Ω为对称部分，表示旋转率张量；S为反对称部分，表示应变率张量。若Q＞0，则代表旋转力克服应变力，另外要求旋涡区域压力低于环境压力，由这2个条件直接提取出旋涡结构。该方法仅适用于强涡实验环境，提取弱涡时有一定误差。

JEONG和HUSSAIN[26]提出λ2方法(第二大复特征值方法)。速度梯度∇v可分解为

由于S2+Ω2为对称矩阵，因此只有实特征值。若S2+Ω2的3个特征值满足第二大特征值小于0，则该位置存在旋涡，并且λ2越小，涡度越大，通过λ2局部最小确定旋涡位置。该方法的缺点是，在旋涡密集区域识别单个旋涡的难度较大。

目前大多数基于点的方法过度依赖阈值，对于同一个流体，阈值的选取会导致不同的实验结果。基于此，LIU等[19]提出了Ω准则来减小阈值对实验效果的影响，后期被归结为第三代旋涡提取方法[56]，如图3所示。

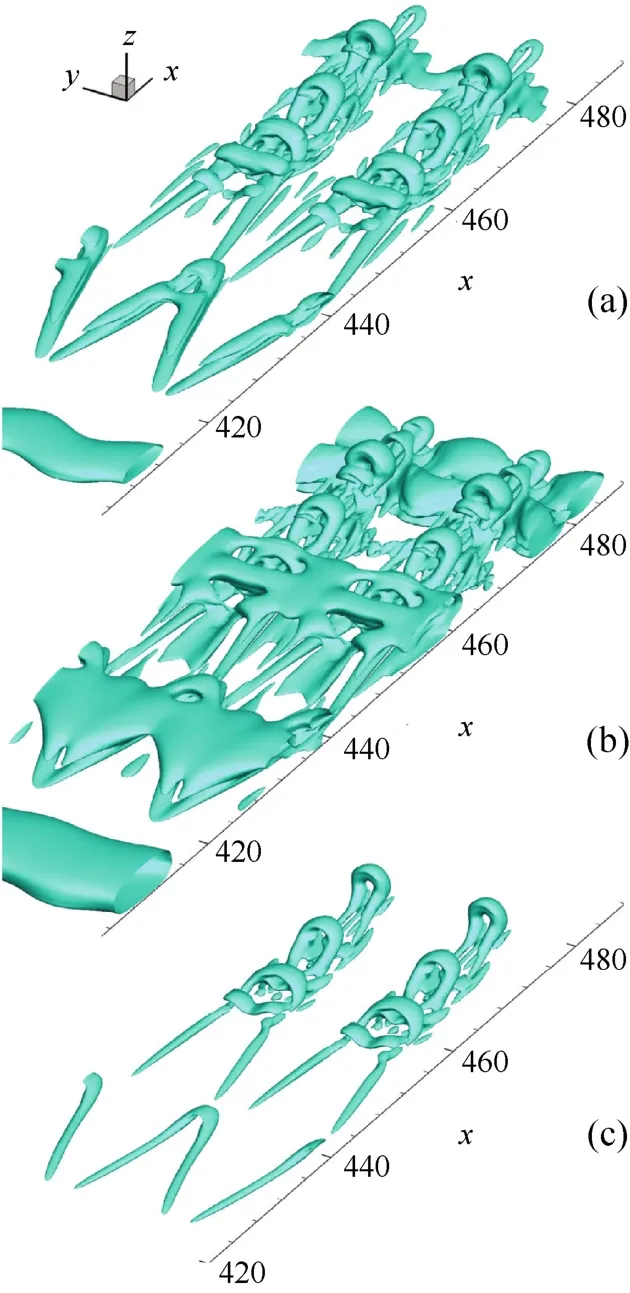
图3 Q准则不同阈值下的结果对比，t=6.8 T ((a) Q=0.001;(b) Q=0.0001; (c) Q=0.01)[19]Fig. 3 Comparison of results under different thresholds of Q criterion, t=6.8 T ((a) Q=0.001; (b) Q=0.0001; (c) Q=0.01)[19]

对于Q准则和λ2准则等方法，目前仍然没有一个阈值能适合所有的旋涡场景。经过ZHANG等[57]的多次验证发现，对于Q准则实验，Q=0.001最优；对于λ2准则实验，λ2=-0.001为最优。相比而言，Ω准则不需要根据实验效果来寻找最适合的阈值，后期研究发现，Ω=0.52时，对所有场景均表现出较好的适应性。

LIU等[19]将Ω准则定义如下：先将式(9)重写为

设

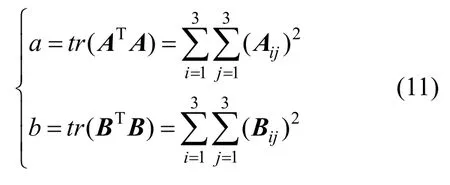
其中，tr是矩阵的迹，另定义一个比值形式，其中，ε为趋于0的正数，确保除数非零。实验表明，结果对Ω的取值并不敏感，一定程度上解决过度依赖阈值的问题。

该方法重新讨论流体速度场分解并将其进一步分解为旋涡部分和非旋涡部分，将Ω的物理意义定义为涡度与涡核内部整体涡度的比值，表明当旋转力强于应变力时将形成旋涡，Q准则和λ2准则对于等值面的物理意义描述则较为模糊。

2.1.3 基于点的方法的问题

大多数方法过度依赖阈值的选取，缺乏普适性；提取弱涡时容易出现假阴性；在参考系变换时效果较差，后期研究对此点进行改进，将Q准则和λ2等经典方法嵌入参考系不变性中；Ω准则解决了阈值问题，但也存在假阳性和假阴性，ε的取值对实验结果也有一定的影响。后期工作中，许多基于点的方法被赋予新的使用限制[58]。

2.2 基于线的方法

2.2.1 特征向量法

SUJUDI和HAIMES[27]提出在三维矢量场中提取旋涡的算法，认为存在涡核线需要满足2个条件：①雅可比矩阵有一个实特征值和一对共轭复特征值；②满足w=u-(u·n)n=0，其中，u为该点速度矢量，n为实特征值对应的单位特征向量。

该方法首先需要找到临界点，即相对于观察者速度为零的点。在该点计算雅可比矩阵特征值，若存在一个实特征值和一对共轭复特征值，即

其中，ui为该点速度矢量；Ci为插值所需参考点的速度矢量。此步骤相当于将速度投影到与实特征值对应的特征向量垂直的平面上。结果为零意味着此处粒子仅沿着特征向量方向移动而不旋转，由此得到涡核位置。该方法为基于线的方法研究提供了良好的基础，但是存在特征值和特征向量复杂运算，线性插值步骤存在误差等问题；并且KENWRIGHT和HAIMES[59]发现特征向量法提取的特征易受其他向量特征影响，若2个旋涡距离较近，提取的旋涡结构会发生一定角度的偏离。

通常平行向量法中至少一个向量会涉及速度梯度，对于Sujudi & Haimes法，有几种平行向量[60]形式。

PEIKERT和ROTH[22]使用平行向量，将Sujudi & Haimes法的特征矢量法等价表示为v||Jv，相比于求解矩阵的特征值和特征向量，矩阵相乘运算的复杂度要小得多；FUCHS等[61]将as||u作为判断依据，其中，as=∇v·u，实特征值对应的单位特征向量n||u。同理，若将速度梯度∇vi(i=1,2,3)作为粒子属性，可将Levy方法表示为

对于WEINKAUF等[28]的方法，可改写为

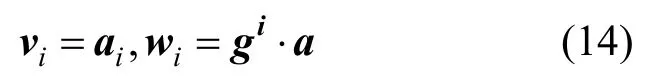
THEISEL和SEIDEL[62]引入特征流场框架，该方法通过将非定常流转换为高维定常流进行计算。WEINKAUF等[28]引入特征流场，将Sujudi &Haimes法的特征矢量法从流线推广到迹线。由于在非定常流中需要考虑时间，因此时间维度需加入到计算中。通过对一维和二维空间的推论，用式(3)表示非定常三维流场中的迹线，雅可比矩阵具有e1，e2，e3，0等4个特征值和各自对应的特征向量，即

在旋涡区域，要求其中2个特征值e1，e2为复数，对应的2个特征向量所在面即为旋涡平面。由共面性质可得，其中，。即

再使用平行向量场搜索所有a||b的点，最终找到涡核。

ROTH和PEIKERT[29]提出了一种利用二阶导数提取涡核线的方法，即发现特征向量法实质上是找到加速度a与速度v平行的点，或者曲率为零的点。一阶导数加速度a和二阶导数b被定义为Jv和速度对于时间的二阶导数。

文献中为涡核线提出了2个新的属性：旋转强度和解的质量；将雅可比矩阵复特征值的虚部作为旋转强度，将涡核与速度矢量之间夹角的余弦作为解的质量，对于实际旋涡而言，这个角度应该小于一定值。这2个新的属性使得用户可以对涡施加新的阈值，以消除弱涡。该方法还引入平行向量场，由此还可与脊线等方法结合。

2.2.2 预测校正方法

SCHINDLER等[30,63]提出一种直接在SPH数据上提取涡核线的算法，即将其分为种子点生成和预测校正2部分。

种子点生成部分需要考虑整体数据集，该部分极大限制了算法的性能。平行向量计算步骤中，该方法未进行常规SPH方法的插值计算，而是直接使用原始数据进行平行向量计算以降低复杂度，经验证发现误差可以忽略。

预测校正部分通过计算平行向量c=(c1,c2,c3)=v×w，并求解梯度∇c1，∇c2，∇c3找出叉积∇ci×∇cj最大的一对i和j，该叉积的方向即为预测方向。若给定一点x，校正点x′=x+s∇ci+t∇cj，其中，s和t的值由

得出，再计算校正点。

与LEVY等[18]、SUJUDI和HAIMES[27]、FUCHS等[61]、WEINKAUF等[28]4种方法优劣势进行对比。该方法在降低时间复杂度方面做出许多改进，如直接使用原始数据进行平行向量计算避免复杂的插值运算；设置容错滤波和旋涡强度，在雅可比矩阵具有虚特征值并且涡核线和速度矢量角度小于45°时识别旋涡，从而过滤微弱特征等。在输出效果上，设置最大连续次数防止涡核线过度分割(图4)，并选用三次插值实现涡核线平滑处理。

2.2.3 基于线的方法的问题

该类方法要对数据集中满足条件的各个数据点进行求解雅可比矩阵特征值等计算，并连接起来形成涡核线特征，在连接和计算过程中存在特征过度分割、时间复杂度较高等难于解决的问题。预测校正法中提到设置最大连续次数以保持连续性[30]，但仍然需要通过实验效果来人为控制连续次数大小；CABRAL等[64-65]结合LIC方法、λ2准则来提取涡核线，并且用矢量箭头来表示粒子旋转方向。

2.3 基于几何曲线的方法

2.3.1 曲率中心法

该方法由SADARJOEN等[31-32]提出。首先对二维流体进行采样，形成能覆盖流体的大量流线。确定每个采样点的曲率中心(图5(a))，对于旋涡区域，曲率中心会趋于一点；对于非旋涡区域，曲率中心无规则性(图5(b))。由曲率中心点网格化形成曲率中心密度(curvature center density, CCD)标量场，再通过设置阈值CCD＞0.8CCDmax来找到旋涡区域。该方法同样存在阈值和弱涡问题，并且真实流体中相邻旋涡的相互作用导致流线形状不规则，存在峰值丢失等问题。

图4 Levy标准(黄色)的涡核线是相连的，Fuchs方法的涡核线(红色)被分割为2个较短部分[63]Fig. 4 The vortex core lines of levy (yellow) are connected, and the vortex core lines (red) of fuchs are divided into two shorter parts[63]

图5 旋涡区域与非旋涡区域[32]Fig. 5 Vortex region and non-vortex region[32]

2.3.2 缠绕角度法

SADARJOEN等[31-32]提出缠绕角概念，在二维流体中选取满足一定旋转条件的流线来提取旋涡。设Si为二维流体中的流线，缠绕角为

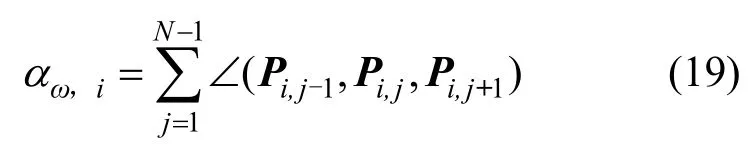
其中，Si由点Pi，j和线段(Pi，j，Pi，j+1)组成，∠(A，B，C)为线段AB和BC之间的夹角。满足如下2个条件时存在旋涡：①流线的缠绕角为2π时得到旋涡，不完全等于2π时得到弱涡[66]；②流线的起始点在终止点附近(由阈值判断)。

该方法大致分为聚类和量化2个步骤。聚类部分将属于同一旋涡的流线归为一组，与属于其他旋涡的流线进行区分；量化部分计算采样点和旋涡的属性，如流线中心、方向、角速度等。与曲率中心法相比，缠绕角度法时间复杂度较高，但在一定程度上可以克服弱涡问题。叶灵伟和冯威[67]提到可通过跟踪流线上的关键点附近区域的流线来避免全局搜索，降低时间复杂度。江俊等[68]选取已提取出的局部对称中心处3×3流线方向场模块I替换式(19)中的Pi，j来计算缠绕角度值，实验证明该方法具有较好的稳定性。

2.3.3 基于几何曲线的方法的问题

经典方法同样受限于阈值，并且时间复杂度相对较高，不能直接扩展到三维空间。对于三维空间问题，REINDERS等[69]改进缠绕角度法，在每个时间步长下的每个水平面中提取二维旋涡并逐一进行连接构造三维涡管。使用特征跟踪方法[70-71]进行实时跟踪，从而在连续的时间步长内提取实时三维旋涡。JIANG等[72]在三维空间中考虑涡核曲率，沿每个点处的流线计算探测向量来探测涡核在特定点的方向矢量，在测量过程中提供了必要的曲率信息，该方法适应于非定常流的涡核提取。陈丽娜和杨冠杰[73]提出角度函数法，用于快速提取涡核区域，通过设置β表示样本点处矢量方向按一定规则变化的程度，β极小点即为涡核点。该方法只能判别大致的涡核区域，但可以很好地解决时间复杂度问题。

3 基于机器学习的流体旋涡提取方法

3.1 基于BP神经网络的方法

XU等[33]设计了一种三层BP神经网络进行流场的智能化特征提取。该方法利用临界点理论，将流场拓扑构成分为临界点和连接临界点的积分曲线，因此识别速度与临界点有密切关系。在临界点提取部分，采用Marching Cubes算法，认为当某个网格单元的4个顶点的8个矢量分量同时存在符号相反时，网格内存在临界点。计算三层结构中隐含层和输出层输出值，再计算输入样本与各类的误差值，其中，dki为第k个标准类的第i个理想输出，yi为实际输出。取其中的最小值Ev，若小于给定阈值，则认为是第v个流场特征。

在时间复杂度方面，训练神经网络作为预处理过程可以忽略不计；特征提取部分的复杂度为O(PLM)，其中P为候选样本区域，L为隐含层节点数，M为输入层节点数。

根据文献中的实验表明，该方法显著减少了数据计算量，并且可以较好地突出流场特征。

3.2 基于CNN的方法

文献[34]提出了一种基于CNN的特征可视化方法，主要研究了二维流场的特征可视化。该方法可以提取流场中用户所需的典型特征和非典型特征并加以分类。与BP神经网络相比，CNN具有较好的识别性，可以有效处理弱涡、变形、平移等情况。

该方法主要分为数据预处理、特征区预选和区域划分3个部分。数据预处理部分主要记录横纵坐标和对应的水平垂直速度分量并对矢量大小进行颜色映射，再通过

对矢量数据进行单位化。特征区预选部分在水平和垂直方向平移窗口矩阵来分割矢量矩阵，将具有相同大小的样本矩阵作为训练后的CNN模型的输入。并判断其特征类别，可将所有具备相同特征的区域归为一类。根据矢量拓扑理论可知顺时针涡、逆时针涡和鞍形特征都包含临界点，因此候选区预选部分主要搜索矢量矩阵的临界点。同2.4.1节中搜索临界点的方法类似，网格单元4个顶点的矢量分量在水平和垂直方向至少正负转换一次时存在临界点，以该网格为中心的样本矩阵作为后续识别的候选区域。通过扫描整个数据集的数据矩阵来获得临界点的大致位置，由此得到候选点列表。区域划分部分由每个候选点得到待识别矩阵，再经训练后的CNN模型进行识别，并将结果存入特征列表用于后续可视化。

实验表明该方法精度高达96.67%，效果优于BP方法，但其需要用户进行多项干预才能使CNN模型达到较好的识别效果，具有主观性。

DENG等[35]提出了一种具有更高的精度和有效召回率的客观旋涡提取方法。该方法包括预处理和涡网2个部分。

预处理部分将物理平面上的非均匀网格转换为均匀网格从而得到其位置和速度信息，使用IVD[74]全局方法标记流场中的点，用0代表非旋涡点，1代表旋涡点，在归一化速度场附近的局部区域进行采样，将这些局部区域和全局标签作为第2部分的数据输入。通过该步骤，可以近似达到全局方法的效果。涡网部分训练CNN模型，直接将测试区域进行输入，通过涡网得到识别结果，从而将输入数据分为旋涡点和非旋涡点。

该方法进行了多组对比实验，如在不同尺寸和形状的流场中验证通用性；与局部方法和全局方法进行对比验证识别精度和速度；与传统机器学习算法相比，可以更好地反映旋涡的分离运动。

3.3 基于机器学习方法的问题

传统的特征提取方法大多数只能提取单一特征，并且需要复杂的数学运算，因此基于机器学习的旋涡提取方法的优势逐渐展现出来。模型可在预处理部分进行训练和学习，实际提取时可忽略训练的时间；训练后的模型可以应用到类似的其他流场中；相比于传统的局部和全局提取方法，有更高的精度和速度。

但是，其局限性也需在后续的研究中加以改进。旋涡识别阶段很难得到用来提取旋涡的标记数据，由于缺乏旋涡的严格数学定义，使得训练网络具有一定的缺陷；在提取精度方面，KIM和GÜNTHER[75]在训练数据时添加噪声并且重采样；模型的通用性较弱，流场的尺寸不定，而部分模型(如CNN)却需要固定大小的输入；数据计算量较大，相比于局部方法，在有高精度的同时仍需要更低的时间复杂度。LIU等[76]提出了一种基于CNN的冲击波提取方法，训练包含多个卷积层的提取网络，该方法具有较好的提取效率和结果。WANG等[77]提出全卷积分割网络旋涡识别方法，在保证精度的同时减少参数数量并降低计算复杂度；大多数方法的训练集缺乏权威性，DUO等[78]对少量由海洋学专家确认的精确旋涡样本进行增强以生成训练集，构建自动识别定位网络OEDNet。

4 参考系不变性

旋涡提取方法可以根据参考坐标系运动的类型分为伽利略不变性、旋转不变性和拉格朗日不变性。不变性是指实验结果(识别的旋涡结构)不随参考系的变化而出现假阳性和假阴性。

大多数旋涡提取方法中，实验结果依赖于观察者的运动，如图6所示。飞行员以不同的路径在矢量场中运动时观察到的场景不同。在标量计算中，实现参考系不变性较为容易，例如两辆同向行驶的列车，以其中一辆列车为坐标系，另一辆的运动距离即为该列车原本的运动距离减去参考列车的运动距离。对于矢量而言，不同参考系的选择会影响旋涡测量的结果，如图7所示。在参考系向右移动时，抵消部分速度，才能显示旋涡。

图6 使用线积分卷积和迹线(黑色较粗)示出3种不同的参考系运动，分别为静止、线性平移和沿正弦曲线移动[79]Fig. 6 Three different reference frame motions are shown using line integral convolution and pathlines (thicker black),which are static, linear translation, and moving along a sinusoidal curve[79]

图7 不同参考坐标系下的对比[80]Fig. 7 Comparison under different reference frames[80]

旋涡提取方法可根据参考系的不同分别选取伽利略不变性、拉格朗日性不变性和旋转不变性，如图8所示。其中，线代表粒子运动轨迹，即迹线；箭头为粒子速度分量方向。伽利略不变性适用于提取等速平移的参考坐标系下的旋涡结构(图8(a))；旋转不变性适于提取绕固定旋转轴旋转的旋涡结构(图8(b))；拉格朗日不变性可以保证无论参考系做任何旋转或平移变换均能得到一致的旋涡结构(图8(c))。

图8 参考系变换下的3种不变量[36]Fig. 8 The three invariants under the transformation of reference frame[36]

4.1 伽利略不变性

参考系以

进行变化时，其中，c0为常数点；c为常向量，若实验结果不随参考系变化，则具有伽利略不变性。

有部分物理量具有伽利略不变性，如加速度、雅可比矩阵等。任何只计算加速度、雅可比矩阵或其导数的方法均具有伽利略不变性。如：Q准则、λ2准则等。伽利略不变性在近年的旋涡提取中应用广泛，JEONG和HUSSAIN[26]强调了伽利略不变性的重要性。SAHNER等[3]提出了利用平行向量提取伽利略不变涡区量的脊线或谷线方法。该方法可以应用于三维空间，通过将脊线或谷线转换为曲面进行提取。

4.2 旋转不变性

旋转不变性参考系以

进行变化，其中，Q(t)为等速旋转矩阵；x0为旋转中心。旋转不变性能保证在参考系等速旋转时准确提取旋涡。该方法的缺点是需要计算旋转中心点x0和三维旋转轴n，如图9所示。在旋转不变性方法中，由Q(t)旋转矩阵将n变化为z轴，旋转不变性雅可比矩阵可表示为

其中，

适用于伽利略不变性参考系中的旋涡提取方法，如Q准则和λ2准则，可以通过旋转不变性雅可比矩阵Jr转化为旋转不变性形式。有

则

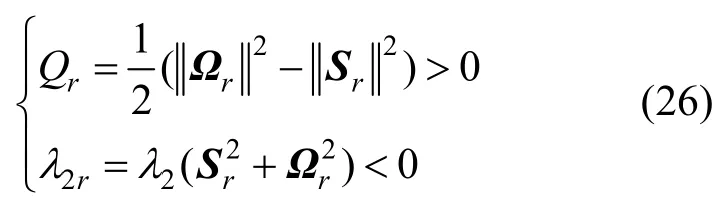
图9 二维和三维旋转不变性[36]Fig. 9 Two-and three-dimensional rotation invariance[36]

GÜNTHER等[36]引入非等距函数gp(x,t)，逆函数hp(x,t)以及转化后的向量场wp，实现笛卡尔坐标系和旋转不变性坐标系相互转换。但是，非等距函数会导致雅可比矩阵离散化，由此提出仅在笛卡尔坐标系下计算旋转不变雅可比矩阵的方法以解决离散化问题。文献中使用多组数据集对比伽利略不变性方法与旋转不变性方法。其中一组实验选用由WIEBEL等[81]在2011年提出的无散度珠流，在一段时间内被旋涡特征可视化领域公认为是评定旋涡提取方法优劣的一个基准。在该对比实验中，发现旋转不变性方法能正确跟踪涡核；伽利略不变性方法的涡核线逐渐偏离迹线，如图10所示。

图10 伽利略和旋转不变性涡核线对比图[36]Fig. 1 0 Galilean and rotation invariant vortices line comparison diagram[36]

4.3 拉格朗日不变性(客观性)

拉格朗日不变性参考系以x′=Q(t)x+c(t)进行变化，其中，Q(t)为实正交矩阵；c为随时间变化的平移向量。拉格朗日不变性方法能够识别进行任何平滑旋转和平移运动的旋涡。向量场中，v，vt，J，a，Ω等物理量均不具有拉格朗日不变性，散度∇v和应变率张量S是向量场中为数不多的具有拉格朗日不变性的物理量[82]。

自拉格朗日不变性的概念出现后，其实验结果基本不受参考系变化影响的特质引起了可视化领域广泛关注，近年来提出了许多经典的拉格朗日不变性形式。

TABOR和KLAPPER[37]将Q准则应用在拉格朗日不变性参考系中，通过

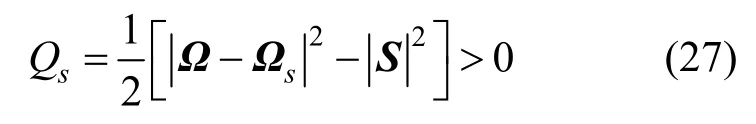
将矩阵Q转化为与应变率张量S相关的形式，其中，Ωs是由应变率张量S的单位特征向量的时间导数组成的矩阵。

DROUOT和LUCIUS[83]定义了旋转率张量的相对值，其中，ΩS为S的特征向量的旋转率张量。MARTINS等[84]运用该相对值并推得拉格朗日不变参考系下的Q准则和λ2准则类似，该文献中还对Δ准则[85]和CHAKRABORTY的局部涡识别方法[86]进行拉格朗日不变性处理。

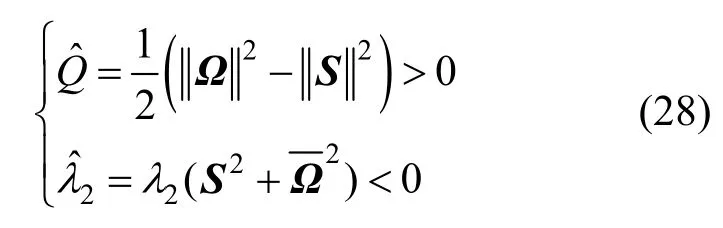
除了对经典方法的改进外，有许多直接应用在拉格朗日不变性的方法。SADLO和PEIKERT[87]将直接Lyapunov指数(directional Lyapunov exponent,DLE)用于提取旋涡。GÜNTHER等[79]通过为域中的每个点计算局部最优参考系得到速度场、加速度场和雅可比矩阵的拉格朗日不变性形式，并且用λ2准则和Sujudi & Haimes法来验证提取的旋涡特征的准确性。GÜNTHER和THEISEL[88]将拉格朗日不变性参考系推广到惯性粒子的涡核提取中，能够提取在任何平滑旋转或平移路径上移动的惯性粒子的旋涡，但是6D平行矢量场的引入使得计算更加复杂，需要研究更快的提取方法。HADWIGER等[38]首先提出了用于非定常流场特征提取的全新客观参考系以计算时变的观察者速度场和近似Killing场，让所有的观察者以各自不同的视角共同观测流场。该方法结合全局和局部参考系，在全局范围内提取的同时也可以进行局部调整，相比GÜNTHER等[79]的方法，其邻域大小固定，普适性较弱。