三参曲线光滑融合的构造及参数的优化

查东东，张 迪，刘华勇

(安徽建筑大学数理学院，安徽 合肥 230601)

在计算机辅助几何设计中，计算容易、结构简单的Bernstein-Bézier曲线，仍存在控制多边形不变时，不能调整曲线外形的缺点。为了克服这一缺点，学术界提出了引入形状参数来构造曲线曲面的思路，例如，文献[1]构造了形状可调的有理三角Bézier基函数；文献[2]将形状及光滑度可调的曲线曲面推广到三角函数空间；文献[3]构造了能精准表示多种曲线的三角多项式均匀B样条；文献[4]分析了平面三角多项式Bézier曲线的形状分区，上述曲线曲面除了继承原有的特性，还能通过形状参数来调整曲线曲面；文献[5]讨论了曲线曲面的较高阶光滑拼接；文献[6]介绍了将曲线曲面混合公式推广到N阶连续的方法；文献[7]融合了2种参数曲线；文献[8]给出了任意逼近多边形的曲线曲面参数样条等。

本文将文献[2]的思路拓展至多项式，提出了三参曲线的拼接算法，构造出的曲线能实现较高的光滑拼接外，还可以用形状参数修改曲线。但曲线在满足融合外，还需对参数的选取做出一定要求，这就要求得对参数选取进行优化。文献[9]构造的过渡曲线曲面既能形状可调，又能保参数方向；文献[10]介绍了曲线能量最小化的形参计算公式；本文又研究了三参曲线的参数选取，借由能量模型，以获得尽可能光顺的曲线[9]。

1 带有形状参数的三参函数的构造

定义1.文献[11]给出了由4个含参数λ的多项式函数构成的函数组

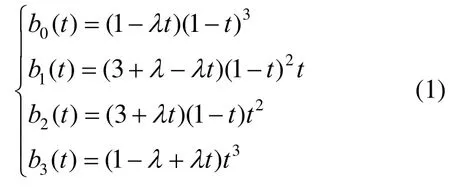
其中，0≤t≤1，-3≤λ≤1，则称

为含有λ，α1，α2的调配函数，简称三参函数，其中0≤t≤1，-3<λ≤1，0≤α1<1，0<α2≤1。

由bi(t)(i=0,1,2,3)的性质，很容易得到三参函数的性质：

性质1.非负性：对于-3<λ≤1，0≤α1<1，0<α2≤1，则有Bi(t;λ,α1,α2)≥0(i=0,1,2,3)。

性质2.权性：由bi(t)的权性易证，，0≤t≤1。

性质3.退化性：当α1=0，α2=1时，Bi(t;λ,α1,α2)退化成bi(t)(i=0,1,2,3)。

性质4.对称性：当α1+α2=1时，B3(1-t;λ,α1,α2)=B0(t;λ,α1,α2)，B2(1-t;λ,α1,α2)=B1(t;λ,α1,α2)。

性质5.端点性质

2 带有形状参数的三参曲线的定义和性质

定义2.给定顶点Pi∈Rd(d=2,3;i=0,1,2,3)，0≤t≤1，称

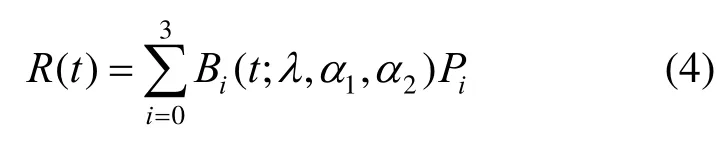
为含有λ，α1，α2的曲线，简称三参曲线，其中Bi(t;λ,α1,α2)为三参函数，-3<λ≤1，0≤α1<1，0<α2≤1。

三参曲线具有以下性质：

性质1.对称性：由三参函数的性质3可知，当确定参数α1+α2=1以及λ时，由仅次序不同的控制多边形与基函数生成的新曲线记作Ci(t)，即有Ci(t)=Ri(1-t)。

性质2.凸包性：由三参函数的权性和非负性可知，其多边形控制的凸包完全包围了三参曲线。

性质3.仿射不变性和几何不变性：三参曲线的形状仅依赖于控制顶点Pi(i=0,1,2,3)，几何变换不改变曲线的形状

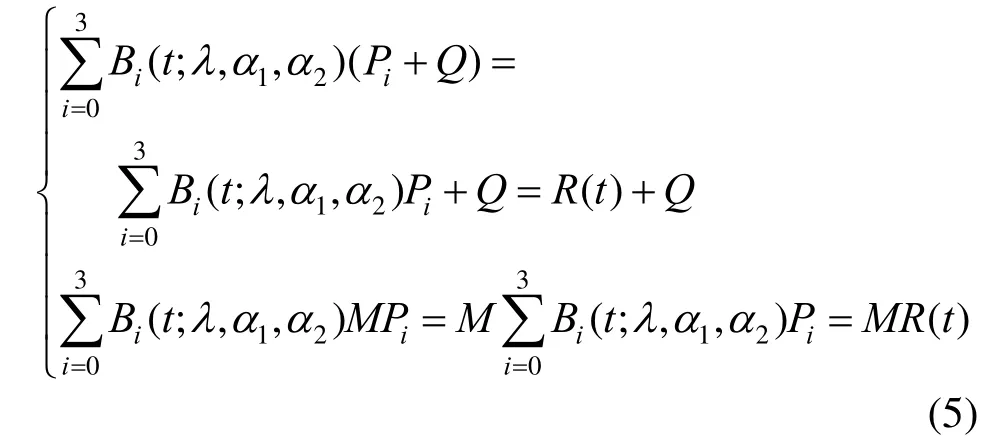
其中，Q为任意向量，且Q∈Rd(d=2,3)；M为任意k×k(k=2,3)阶矩阵。

性质4.端点性质

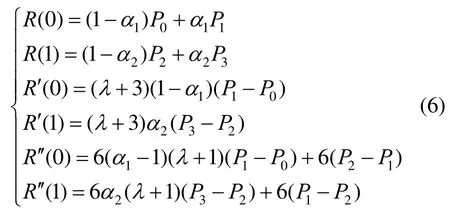
性质5.形状可调性：三参曲线会随着给参数λ，α1，α2选择不同的值，曲线形状被调整的程度也各不相同。

图1(a)~(c)是依次仅改变单一参数，而其他参数取值不变时所获取的三参曲线。在图1(a)中，固定λ，α2取值，从上至下取α1=0.8，0.5，0.2；图1(b)中，固定λ，α1值，从上至下取α2=0.2，0.5，1；图1(c)中，固定α1，α2值，从上至下取λ=1，0，-1。由此可看出各参数的效果：4个控制顶点从左往右依次为P0，P1，P2，P3，则α1确定曲线在控制多边形边P0P1上的起点，α2确定曲线在边P2P3上的终点，而λ越大，曲线整体就越靠近控制多边形P0P1P2P3。

3 带有形状参数的三参曲线融合

3.1 带形状参数的三参曲线的拼接

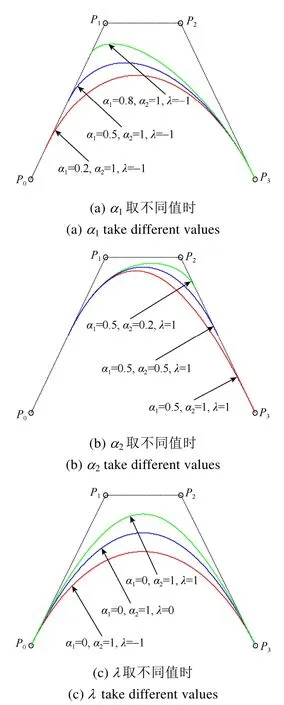
图1 α1，α2，λ分别取值不同时对曲线的影响Fig. 1 The influence of different values of α1, α2, λ on the curve

定理1.满足时，R1(t)和R2(t)在连接点处满足G2连续。

证明：由曲线端点性质可知

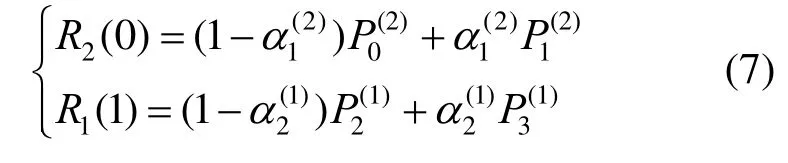
即曲线满足G0连续；又由端点性质可得

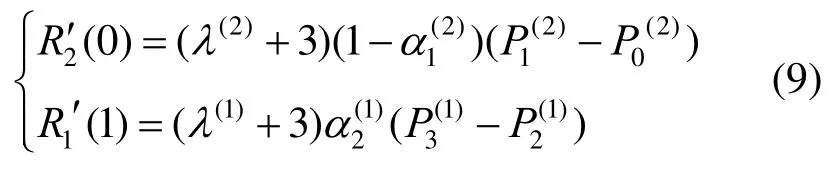
则有

故曲线满足G1连续，其中，；又由端点性质可得

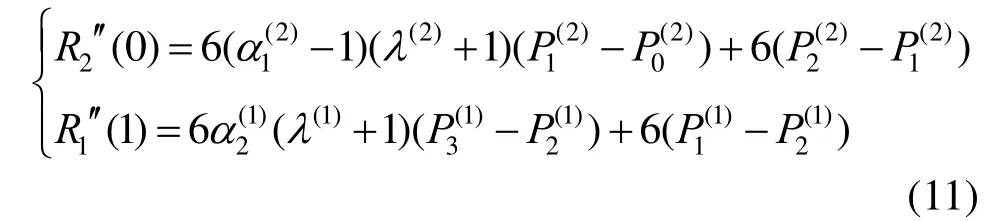
则有

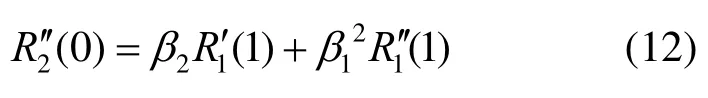
故曲线满足G2连续，其中，

由定理1表明，若能做到R1(t)的控制多边形的边和R2(t)的控制多边形的边重合，且满足，则R1(t)和R2(t)自动满足G2连续。图2给出了不同参数取值下的R1(t)，R2(t)实现G2连续的实例。其中，箭头为曲线的曲率。

3.2 带形状参数的三参曲线的组合及应用

定义3. 假设给定了2l+2 (l≥1)个控制顶点Pi∈Rd(d=2,3;i=0,1,2,···,2l+1)，0≤t≤1，以及形状参数，可以定义第j(j=1,2,···,l)段组合三参曲线为

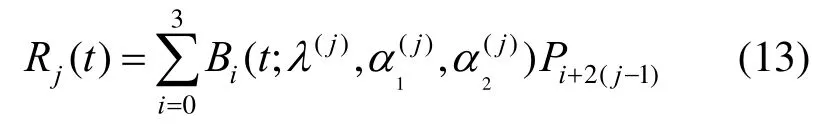
组合的三参曲线具有以下共同点：①每个控制多边形及基函数决定一段三参曲线；②确定控制多边形后，每相邻两段的三参曲线能够实现G2连续的拼接；③每段三参曲线的形状参数都不同，也可在给定若干对控制顶点时，组合三参曲线可以依靠形状控制参数来实现闭合曲线。

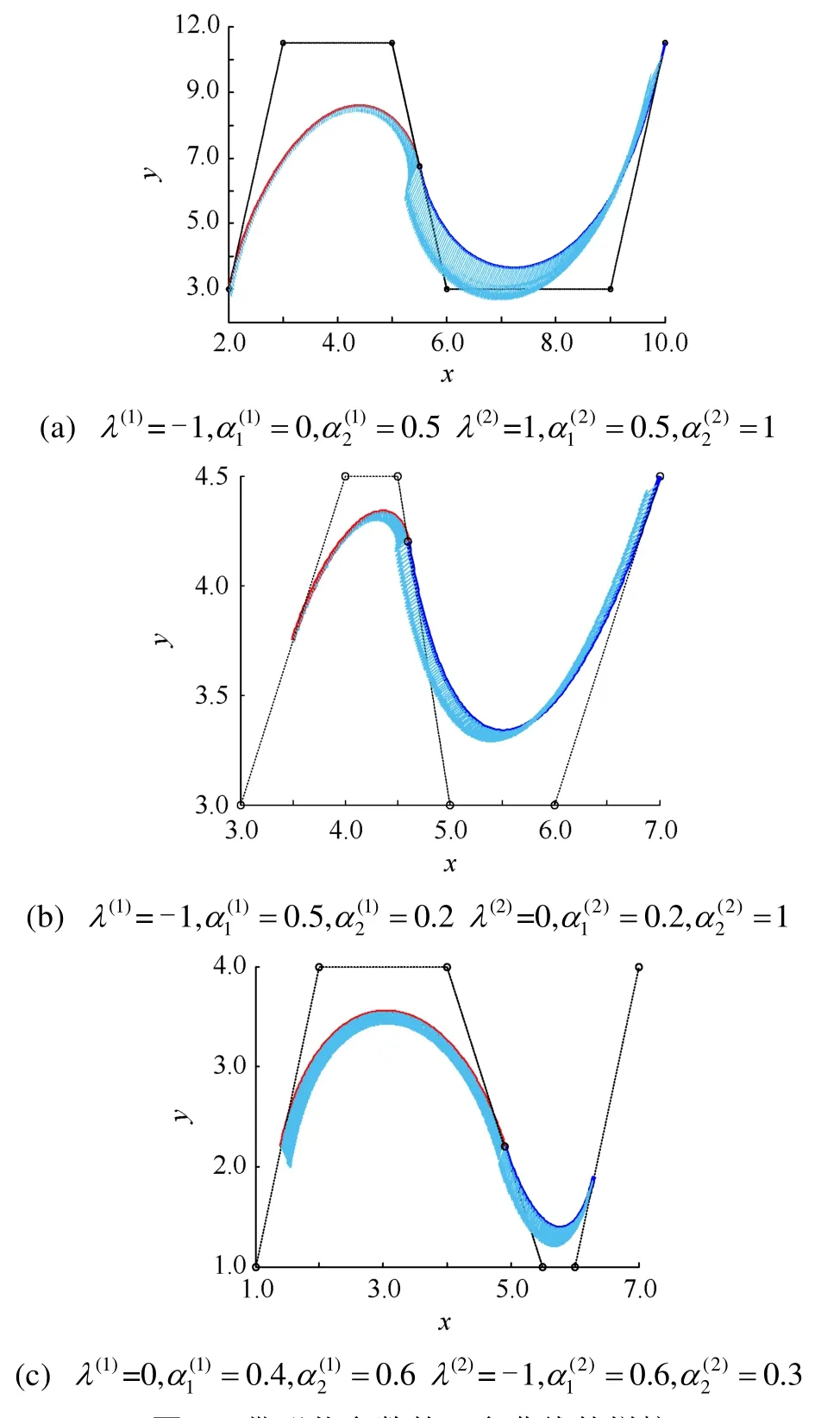
图2 带形状参数的三参曲线的拼接Fig. 2 Blending of three-parameter curves with shape parameters

此外，还将三参曲线与原基函数曲线、三次B样条曲线进行了比较：①以控制多边形为目标函数，引入均方根误差(root mean square error, RMSE)来衡量曲线到控制多边形的逼近程度。以单段曲线为例，给定顶点P0=(1,2)，P1=(1,3)，P2=(3,3)，P3=(3,2)，三参曲线和原基函数曲线共同参数λ=0，三参曲线其他参数为α1=0.5，α2=0.5，算出三参曲线的RMSE值为0.280 2，小于原基函数曲线的RMSE值0.564 1，故三参曲线比原基函数曲线更贴近控制多边形，如图3所示；②比较3种算法的时间复杂度，在本机实验中，借助Matlab使用tic+函数+toc的方法计算出各种算法的运行时间，以运行时间近似替代。为减少误差，故算法运行时间的选取为：每种算法一组实验执行100次算法循环，取其运行时间的平均值，做10组实验，再取10组平均运行时间的最优值，再比较3种算法的运行时间最优值，多次实验后可以看出，改进算法略为领先，但三者相差不大；③满足G2连续的条件，三参曲线要比原基函数曲线简单，同时三参曲线还具有调节曲线形状的优点。不同算法的性质对比见表1。

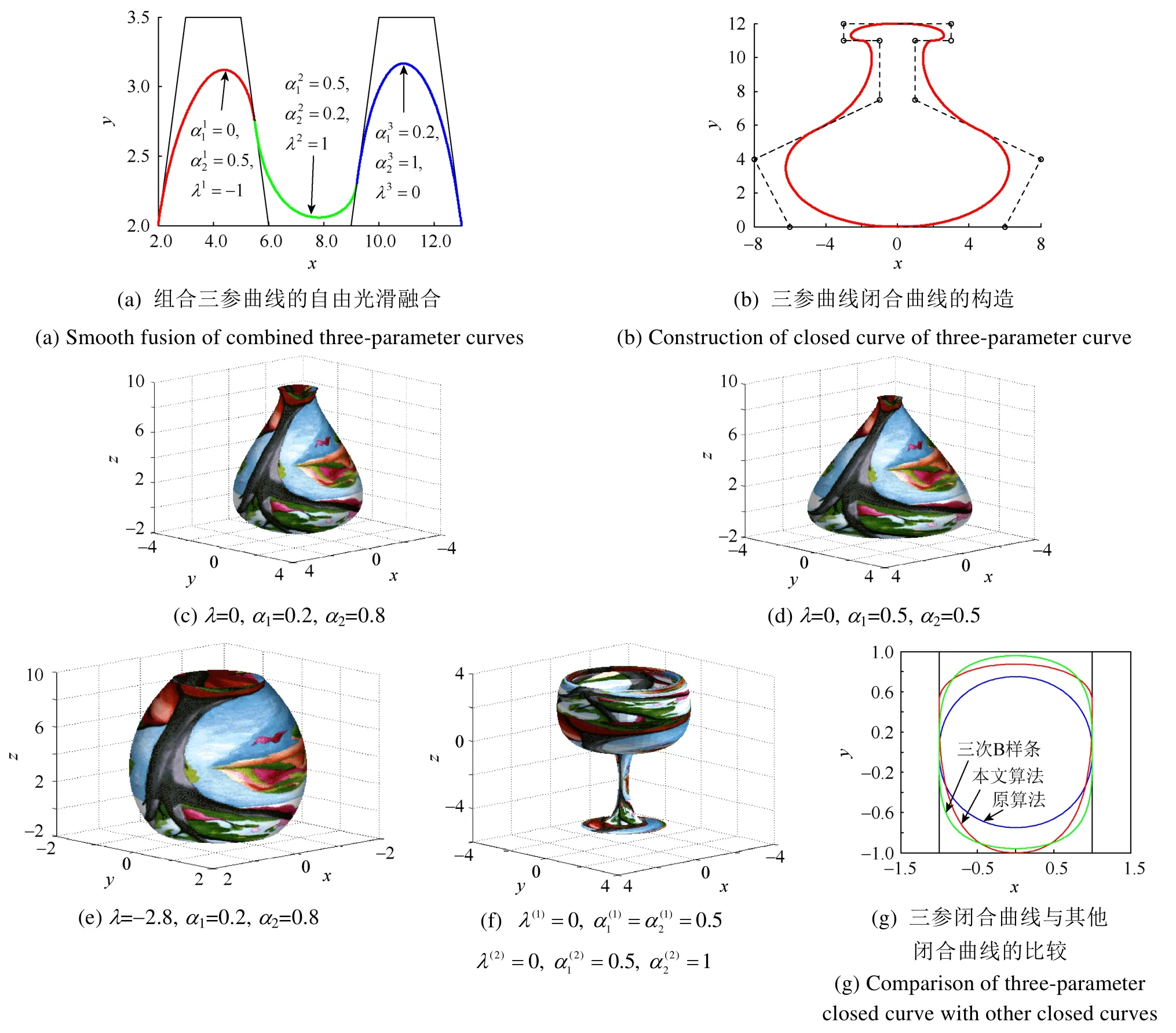
图3 组合三参曲线的自由光滑融合和应用Fig. 3 Smooth blending and application of combined three-parameter curve

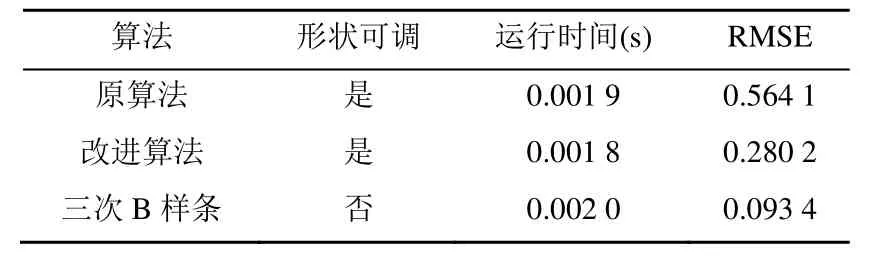
表1 不同算法的对比Table 1 Comparison of different algorithms

4 基于最小弯曲能量选取最优参数

由定义2可将三参曲线R(t)分别写成固定其他两个参数，讨论一个单独参数的形式，即

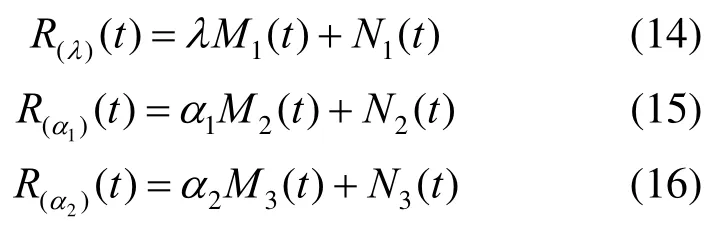
其中，

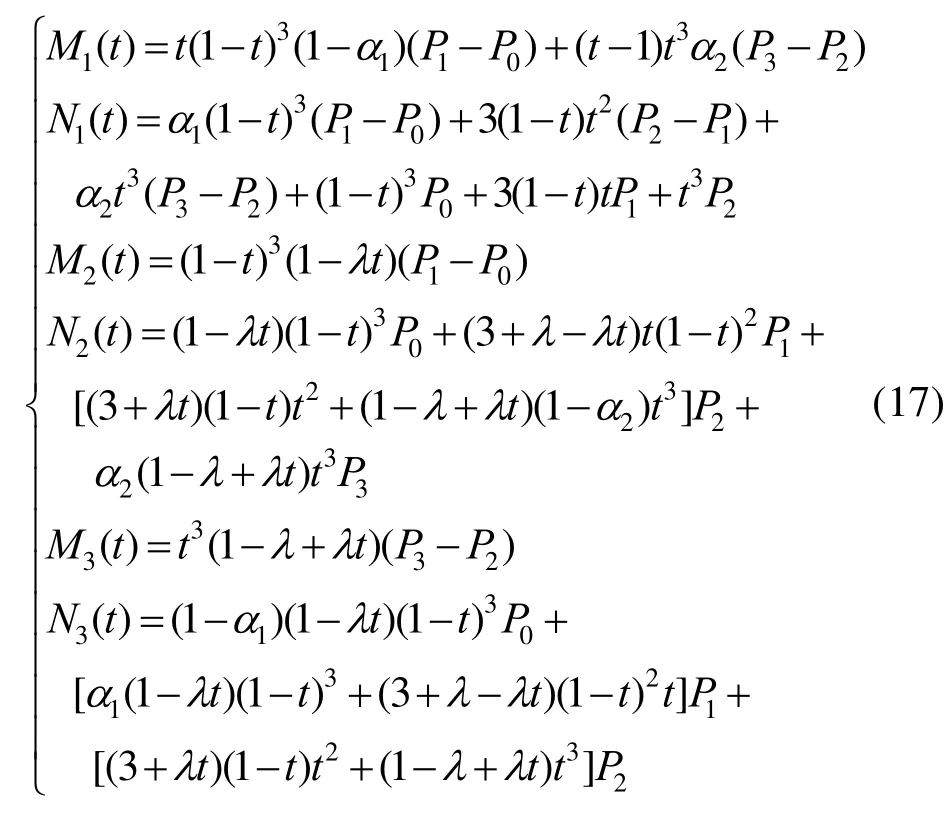
光顺准则[12]提出，曲线R(t)的光滑程度可近似地由能量值来刻画，Ec越小，则曲线R(t)越光顺。为了使能量值Ec尽可能小，在顶点和参数α1，α2取值已经被确定时，只需再考虑λ的取值，得能量方程为

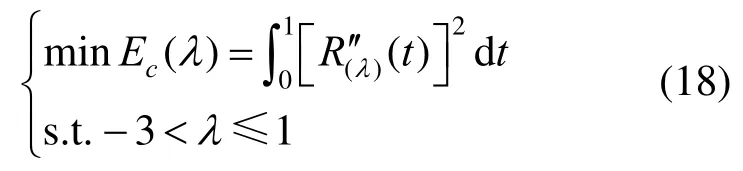
将式(14)代入式(18)，经过整理得

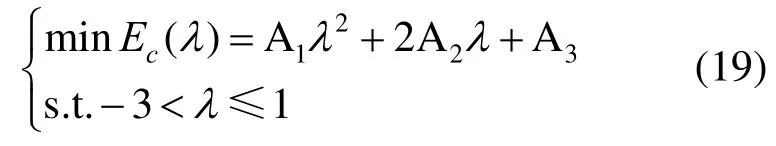
其中，Ai(i=1,2,3)为常数，分别为，。

例1.有P0=(2,0),P1=(3,3),P2=(5,3),P3=(6,0)，形状参数α1=0.5，α2=0.5，求得A1=3，A2=-9，A3=27，获得能量方程为

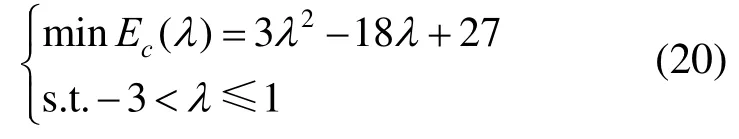
又因为-3<λ≤1，故取λ=1时，获得最小弯曲能量minEc（λ）=12，如图4所示。

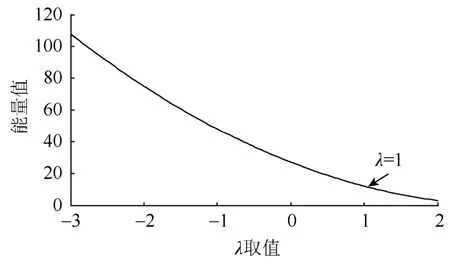
图4 α1，α2确定时三参曲线能量值曲线Fig. 4 Energy value curve of three-parameter curve when α1, α2 is determined

同理，在顶点和参数λ，α2取值已经被确定时，只需再考虑α1的取值，得能量方程为

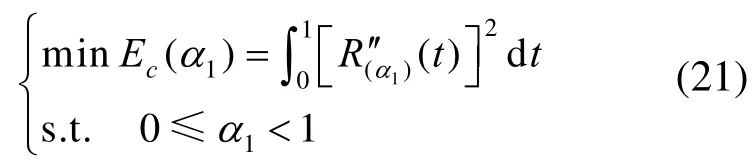
将式(15)代入式(21)，经过整理可得

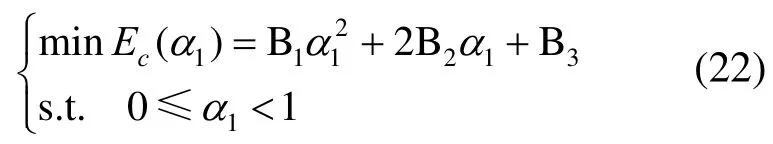
其中，Bi(i=1,2,3)为常数，分别为，。

例2. 有P0=(2,0),P1=(3,3),P2=(5,3),P3=(6,0)，形状参数α2=1，λ=-1求得B1=24/5，B2=0，B3=48，获得能量方程为

又0≤α1<1，故取α1=0时，得minEc(α1)=48，如图5所示。

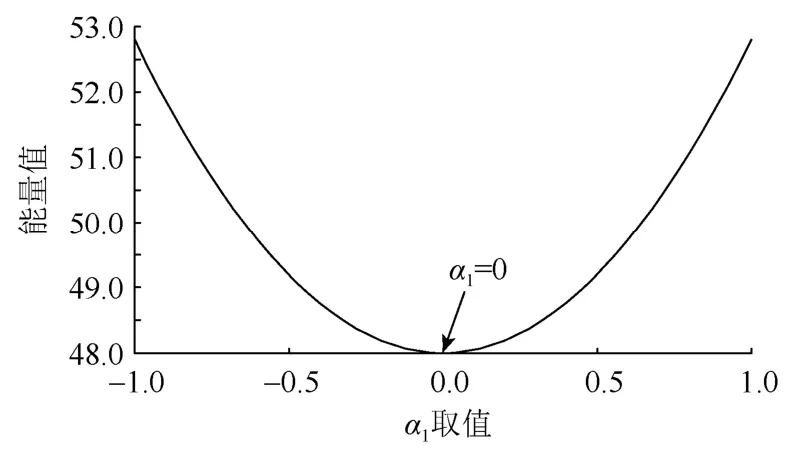
图5 λ，α2确定时三参曲线能量值曲线Fig. 5 Energy value curve of three-parameter curve when λ, α2 is determined

同理，在顶点和参数λ，α1取值已经被确定时，只需再考虑α2的取值，得能量方程为

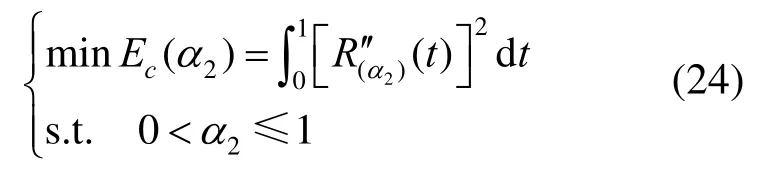
将式(16)代入式(24)，经过整理可得

其中，Ci(i=1,2,3)为常数，分别为，。

例3.有P0=(2,0),P1=(3,3),P2=(5,3),P3=(6,0)，参数α1=0.5，λ=1求得C1=144/5，C2=-132/5，C3=156/5，获得能量方程为

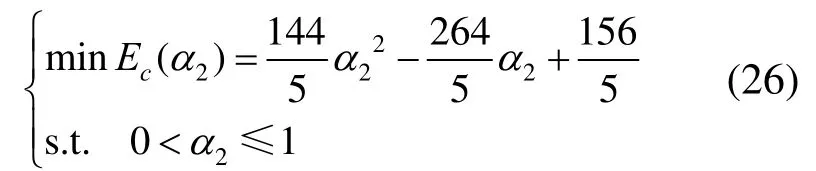
又因为0<α2≤1，故取α2=11/12时，得到最小弯曲能量minEc(α2)=7，如图6所示。

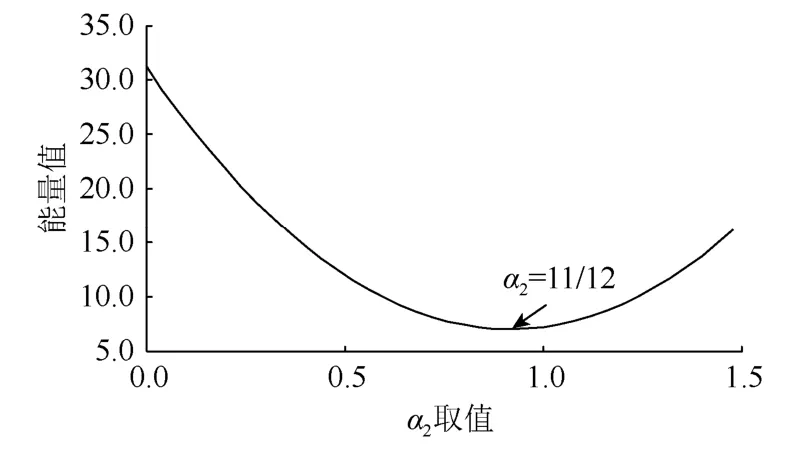
图6 λ，α1确定时三参曲线能量值曲线Fig. 6 Energy value curve of three-parameter curve when λ, α1 is determined

依次将图4~6和图1(a)~(c)分别对比，可看出：①在参数α1，α2固定时，λ取值越大，三参曲线弯曲能量越小，此时三参曲线越逼近控制多边形；②当λ，α1固定时，α2取值越大，三参曲线弯曲能量越小；③而λ，α2固定时，α1取值越大，三参曲线弯曲能量反而越大；但后两种情况有一共同点：此时的三参曲线均为越远离控制多边形，弯曲能量越小，这是由其参数对称性所决定的，且α1，α2分别确定曲线的起始点。

进一步考虑三参曲线组合时的最优参数选取，以3.2节的组合三参曲线为例，在保证每个控制多边形构造的三参曲线满足G2连续的情况下，同时对每段曲线加以最小弯曲能量约束，最终得到唯一确定的具有能量约束的组合三参曲线。

类比式(16)~(17)可以将第j段三参曲线Rj(t)(j=1,2,···,l)依次写作

由式(13)和能量准则可知，第j段三参曲线的能量值为

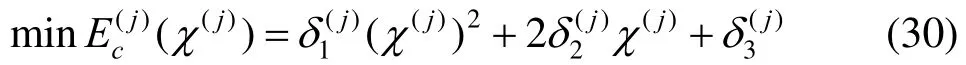
其中，i=1,2,3，且

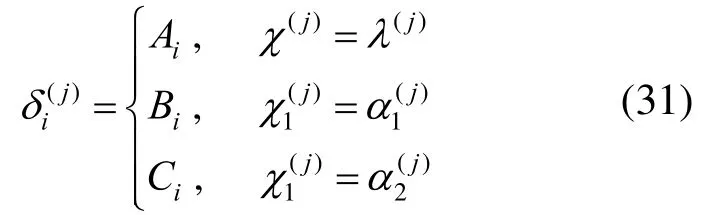
在保证组合曲线满足G2连续的同时，选择最优的参数，故对l段组合三参数曲线，给定下列能量方程为

例4.有(7,3.5)，形状参数为，，分别求得获得能量方程为

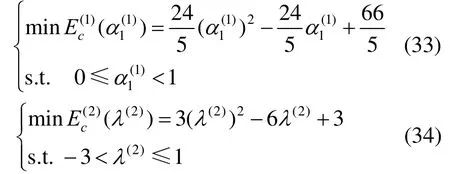
图7(a)中箭头是曲线的曲率，图7(b)是曲线拼接点处曲率的放大图。优化后的曲线还是可以实现G2连续，图7(c)标注了未优化的曲线和优化的曲线最大曲率点，图7(d)给出了未优化的第一段曲线和优化的第一段曲线的曲率对比。显然，关于最高曲率，未优化曲线比优化曲线要大；其次，曲线整体曲率上，未优化的曲线也是比优化曲线要大。故优化后的曲线具有更小的弯曲能量。

图7 形状参数的选取Fig. 7 Selection of shape parameters

5 结束语

本文构造了带有形状参数的三参函数，在继承原有性质外，曲线满足G2连续的融合条件也比较简单，本文中给出了一些参数不同取值下的曲线形状可调的实例。此外，本文利用最小能量值来选取最佳参数，可以看出各参数取值不同，曲线能量也各异，故选取最佳参数有助于过渡曲线尽可能光顺。但这是基于单参数的优化，有关多参数的同

时优化问题还有待研究和解决。