两个物体运动的相关性分析
2020-11-13福建姚龙楷
福建 姚龙楷
质点运动是每年高考的必考内容,重点考查主要概念和基本运动规律。在实际生产、生活中也经常出现几个物体同时参与运动的物理过程。要解决这样的问题要求我们对运动学规律有深刻的理解。本文通过对两个物体运动相关性问题进行分析研究,促使考生建立一个正确空间观念,培养良好的空间想象能力和数学分析能力。
一、互不牵连的相关运动
物体做何种形式的运动,是由它的受力情况和初始状态共同决定的,物体有其自己的运动规律,一般说来,与其没有力相关联的其他物体的运动是不相关的。但是,在一定的空间条件下,会涉及与其他物体运动的相互关系问题,我们称之为互不牵连的相关运动。
1.两条直线运动的相关性
【例1】甲、乙两车在一条直线上同时沿相同方向运动,甲车在乙车前x=56 m处,甲车以初速度v1=16 m/s、加速度大小为a1=2 m/s2匀减速刹车,乙车以初速度v2=4 m/s、加速度大小为a2=1 m/s2做匀加速运动,求:
(1)乙车追上甲车前二者间的最大距离;
(2)乙车追上甲车所需时间。
【解析】(1)在开始阶段,甲车在前、乙车在后,且甲车速度比乙车大,两车距离一直增大,设运动时间为t时速度相同,设此时速度为v,根据运动学公式vt=v0+at得
v1-a1t=v2+a2t
代入数据解得t=4 s,v=v1-a1t=8 m/s
此后甲车减速、乙车还在加速,两车距离缩短,所以在速度相等时两车距离最大,最大距离为
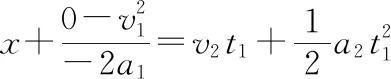
联立解得t1=12 s
【点评】1.质点的“追及”类问题,重要的是在同一直线坐标轴上把握两质点之间的位移关系和时间关系。
2.对于在一条直线上运动的两个物体的追及问题,可分为如下两类情景:
(1)速度大者减速(如匀减速直线运动)追速度小者(如匀速运动)。
①两者速度相等时,追者位移仍小于被追者位移与初始间距之和,则永远追不上,此时两者间有最小距离。
②当两者速度相等时,若追者位移恰等于被追者位移与初始间距之和,则刚好追上,也是两者相遇时避免碰撞的临界条件。
③若相遇时追者速度仍大于被追者速度时,则被追者还能再一次追上原来的追者,两者速度相等时,两者间距离有一个较大值。
(2)速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动)
①当两者速度相等时,两者间有最大距离。
②当追者位移等于被追者位移与初始间距之和时,后者追上前者即相遇。
【例2】A球自距地面高h处开始自由下落,同时B球以初速度v0正对A球竖直上抛,空气阻力不计。问:
(1)要使两球在B球上升过程中相遇,则v0应满足什么条件?
(2)要使两球在B球下降过程中相遇,则v0应满足什么条件?
【解析】本题涉及两个物体的运动不是单一方向,但相遇条件仍然是同一时刻到达同一位置。此时两球相遇时位移之和等于h。即



(1)欲使两球在B球上升过程中相遇,则有
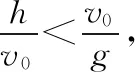
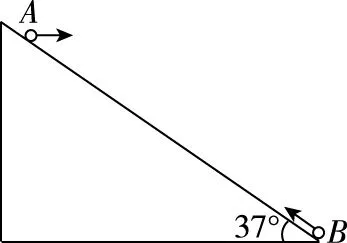
(2)欲使两球在B球下降过程中相遇,则有t1 (1)B球上升过程中A球与相遇,即vB>0, (2)B球下降过程中A球与相遇,即-v0 【例3】如图1所示,一足够长倾角为37°的斜面固定在水平地面上,质量为m的小球B从斜面的底端开始以初速度10 m/s沿斜面向上运动,与此同时质量为m的小球A在斜面上某点以水平初速度抛出,不计空气阻力。已知小球A落到斜面时恰好与小球B相撞(不考虑二次相撞),此时小球B速率为4 m/s,小球B与斜面间的动摩擦因数μ=0.5,重力加速度g取10 m/s2。求:小球A的初速度以及抛出点距地面的高度。(sin37°=0.6,cos37°=0.8) 图1 【解析】由“已知小球A落到斜面时恰好与小球B相撞”可知可能是小球B在向上运动减速过程中相撞,也可能是小球B速度减为0后反向加速过程中相撞,故两种可能都要分析。 (1)小球B沿斜面做匀减速直线运动,有 mgsin37°+μmgcos37°=ma1得a1=10 m/s2 速率减为v1=4 m/s时 由v1=vB-a1t1解得t1=0.6 s 解得v01=4 m/s 因此H1=y1+s1sin37°=4.32 m (2)小球B速度减为零再反向加速过程中相撞的情景请同学们动手计算(答案H2=45.6 m)。 【点评】(1)研究平抛运动的基本思想是将其分解为沿水平方向的匀速运动和竖直方向上的自由落体运动。涉及斜面上的平抛运动,可利用斜面三角形的边角关系,提炼出斜面上的约束条件。常见的模型如下: 方法内容斜面总结分解速度水平方向vx=v0竖直方向vy=gt合速度v=v2x+v2y分解速度,构建速度三角形,满足cotθ=vyvx=gtv0分解位移水平方向x=v0t竖直方向y=12gt2合位移s=x2+y2分解位移,构建位移三角形满足tanθ=yx 【例4】如图2所示,在竖直线OM上某点A水平向右抛出一小球A的同时在B点水平向左抛出另一小球B,两小球恰好在斜线ON上的Q点相遇,已知A球是第一次经过斜线ON且Q点离O点的距离是最远的,OQ=L,B球是以最短位移到达Q点的,∠MON=θ,重力加速度取g,求: 图2 (1)OA间距离h; (2)A、B球的初速度v1、v2。 由平抛运动规律可知 小球A在水平方向位移为x=v1t 由图3可知x=Lsinθ且y+h=Lcosθ 图3 又x=Lsinθ=v1t 【点评】两个小球各自遵守平抛运动规律,互不干扰。但两球的运动时间是相同的,这是重要的关联点。本题理解的要点在于读懂Q点离O点最远的含义及B球是以最短位移到达Q点的含义,即小球A的运动轨迹在Q点正好与OQ相切且QB⊥ON,再利用几何关系及相关公式便可求解。 【例5】如图4所示,虚线MN是一垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感强度为B的匀强磁场,方向垂直纸面向外。O是MN上的一点,从O点可以向磁场区域发射电荷量为+q、质量为m、速率为v的粒子,粒子射入磁场时的速度可在纸面内各个方向。已知先后射入的两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L。不计重力及粒子间的相互作用。 图4 (1)求所考查的粒子在磁场中的轨道半径; (2)求这两个粒子从O点射入磁场的时间间隔。 【解析】从分析粒子射入磁场所做匀速圆周运动的圆心位置与粒子射入磁场时速度方向的关系入手,找到两个粒子的轨道相交于P点的条件。 (2)如图5所示,以OP为弦可画两个半径相同的圆,分别表示在P点相遇的两个粒子的运动轨迹。圆心和直径分别为O1、O2和OO1Q1、OO2Q2,在O处两个圆的切线分别表示两个粒子的射入方向,用θ表示它们之间的夹角。由几何关系可知 图5 ∠PO1Q1=∠PO2Q2=θ 从O点射入到相遇,粒子1的路程为半圆周加弧长Q1P,则 Q1P=Rθ 粒子2的路程为半个圆周减弧长PQ2,则 PQ2=Rθ 其中T为圆周运动的周期.粒子2运动的时间为 两粒子射入的时间间隔为 【点评】1.求解带电粒子在匀强磁场中做匀速圆周运动的问题,其解题思路是先做到“三定”:即定圆心、定半径、定圆弧对应的圆心角。本题中众多粒子的运动半径R简单可求,所有粒子做匀速圆周运动的圆心集合是以O点为半径的半圆(处在过O点的水平线下方180°范围内),其中必有两个圆的弦是以OP为线段的。从而可以作出正确图示并求解。 2.在解物理问题时,画图能帮助我们准确地理解题意,当学生能把习题的文字叙述转化成一幅图象,表明学生通过审题已掌握了试题的主要内容。在画图时,有时还能发现自己对试题理解上存在问题。画图又能帮助你分析问题。把图示正确画出来,问题往往已解决了一半。在学习中,重视画图是一种良好的学习习惯和素养。 两个物体之间通过相互作用力,从而使两个物体的运动相互影响,相互制约,我们称之为互相牵连的相关运动。这类问题的综合性强,一般可按如下基本步骤分析。 【例6】用轻弹簧相连的质量均为2 kg的A、B两物块都以v0=6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量为4 kg的物块C静止在前方,如图6所示,物块B与物块C碰撞后二者粘在一起运动,则在以后的运动中 图6 (1)当弹簧的弹性势能最大时,物块A的速度为多大? (2)弹簧弹性势能的最大值是多少? (3)物块A的速度方向有可能向左吗?为什么? 【解析】(1)B、C发生碰撞时,B、C组成的系统动量守恒,设碰后瞬间,B、C两者速度为v,则有 mBv=(mB+mC)v 解得v=2 m/s 此后A、B、C继续运动,弹簧被压缩,当A、B、C三者的速度相等(设为v′)时,弹簧的弹性势能最大,由于A、B、C三者组成的系统动量守恒,则有 (mA+mB)v0=(mA+mB+mC)v′ 解得v′=3 m/s (2)A的速度为v′时,弹簧的弹性势能最大,设其值为Ep,根据能量守恒定律得 解得Ep=12 J (3)根据系统动量守恒定律得 (mA+mB)v0=mAvA+(mB+mC)vB 设A速度向左,则vA<0,解得vB>4 m/s 则B、C发生碰撞后,A、B、C三者的动能之和为 实际上系统的机械能为 所以A不可能向左运动。 【点评】1.一个物体在弹簧弹力作用下的受力分析和运动分析: 2.在由两个物体和弹簧组成系统的运动中,具有下面的特点: (1)两个物体速度相等时,弹簧处于形变量(压缩或拉伸)最大的状态,弹簧的弹性势能达到最大。 (2)两个物体在持续变化的弹力作用下做变加速运动,不能采用运动学公式来解决。但此模型属于弹性碰撞模型,所以满足包括弹簧在内的系统动量守恒和系统机械能守恒。 【例7】如图7所示,长为L的长木板A放在动摩擦因数为μ1的水平地面上,一滑块B(可视为质点)从A的左侧以初速度v0向右滑上A,B与A间的动摩擦因数为μ2(A与水平地面间的最大静摩擦力与滑动摩擦力大小相同)。已知A的质量为M=2.0 kg,B的质量为m=3.0 kg,A的长度为L=2.5 m,μ1=0.2,μ2=0.4(g取10 m/s2)。 图7 (1)A、B刚开始运动时各自的加速度分别是多大? (2)为保证B在滑动过程中不滑出A,初速度v0应满足什么条件? (3)在满足(2)中条件的情况下,分别求出A、B对水平地面的最大位移。 【解析】(1)分别对A、B进行受力分析,根据牛顿第二定律得Ff1=maB,Ff1-Ff2=MaA A的加速度大小 (2)当A、B速度相等时,若B恰好运动到A的右侧末端,则可保证B不会滑出A,设经过时间t,A、B的速度相等,则有v0-aBt=aAt 代入数据解得t=1 s,v0=5 m/s 所以初速度应满足v0≤5 m/s (3)B恰好不滑出A时,A、B对水平地面的位移最大,A、B速度相等后相对静止,一起以v=aAt=1 m/s的初速度做匀减速运动直到静止。 匀减速运动的加速度大小为a=μ2g=2 m/s2 所以A发生的位移为sA+s=0.75 m B发生的位移为sB+s=3.25 m 【点评】1.“滑块、滑板”模型分析方法:(1)分析滑块和木板的受力情况:整体法、隔离法仍是基本的研究方法,并根据牛顿第二定律求解加速度;(2)分析滑块和木板的运动情况:找出滑块和木板之间的位移关系或速度关系,建立方程。特别注意滑块和木板的位移都是相对地面的位移。 2.涉及两个物体、多个运动过程,并且物体间还存在相对运动,应采用隔离法,准确求出各物体在各运动过程的加速度,找出物体之间的位移(路程)关系或速度关系是解题的突破口。求解中更应注意两个过程的联系:上一个过程的末速度是下一个过程的初速度。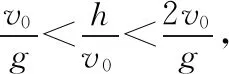
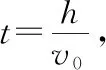

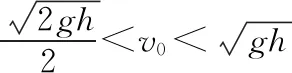
2.直线运动与曲线运动的相关性



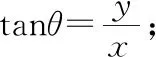
3.两种曲线运动的相关性

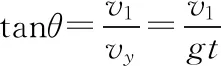







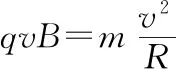

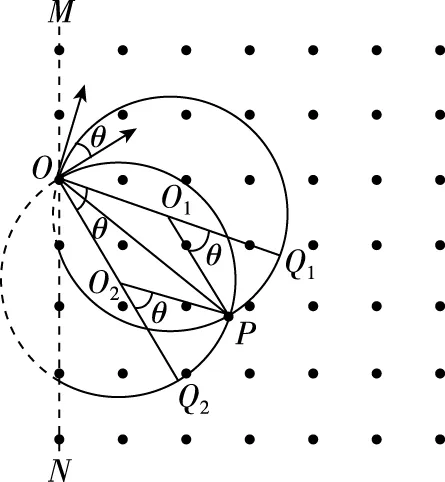
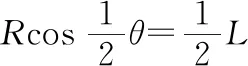
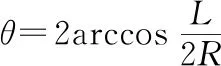
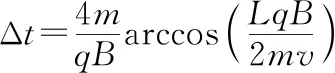
二、互相牵连的相关运动