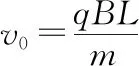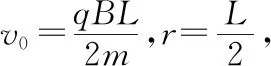理想边界“嵌入型”交变磁场模型的解题策略

福建 郭 威

带电粒子在有界磁场中的运动备受高考命题者的青睐，是历年高考中的一个重要考点，有关理想边界“嵌入型”交变磁场的题型对学生的核心素养和应用数学处理物理问题的能力有一定的要求，最近几年在各地模拟考试题中时有出现，但测验的结果不尽如人意，因此此类问题成为了教学中一个新的难点。学生遇到此类题型，不是无从下手就是漏答、漏解错失分数，究其原因，关键还是在于未能深入掌握该题型的命题特点和解题策略，一旦掌握了该模型的解题策略，此类问题将迎刃而解，难点不再难。

一、理想边界“嵌入型”交变磁场模型的特点

理想边界“嵌入型”交变磁场的情景为在较大的磁场中嵌入一个区域磁场，其模型特点为：

1.“嵌入型”磁场方向一般与外磁场方向相反，与外磁场构成交变磁场，只受洛伦兹力的带电粒子在理想边界的“嵌入型”交变磁场中运动具有往复性，轨迹就会在交变磁场中形成一条连续的反转曲线；

2.“嵌入型”磁场的形状为不同几何形状的磁场区域，可为圆形、半圆形、三角形、正方形等几何形状与外磁场构成有理想边界的交变磁场；

3.带电粒子在磁场中运动的半径与入射的速度、磁场的大小及方向有关，条件不同，轨迹不同，可一旦题设条件为带电粒子的入射初始点相同，到达终点相同，带电粒子在交变磁场中回旋往复运动的情景因具有周期性与对称性的特点，速度的大小与运动时间将是一个多解问题。

二、理想边界“嵌入型”交变磁场模型的解题策略

1.利用“等分法”和“周期性”求解粒子入射速度大小

【调研试题1】如图1所示，直线CD下方无磁场，上方空间存在两个匀强磁场，其分界线是边长为a的正方形PMQN，内外的磁场方向相反且垂直于纸面，磁感应强度大小都为B，现有一质量为m，电荷量为q的带负电微粒从P点沿边长向左侧射出，要求微粒始终做曲线运动并最终打到Q点，不计微粒的重力，外部磁场范围足够大，求：从P点到Q点，微粒的运动速度大小。

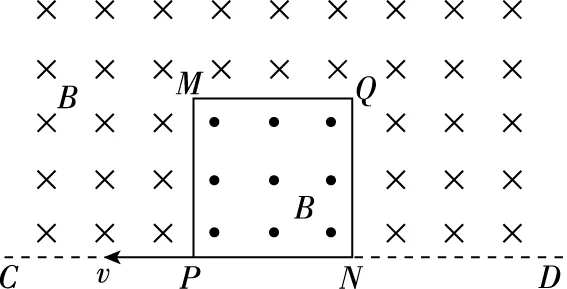
图1

图2

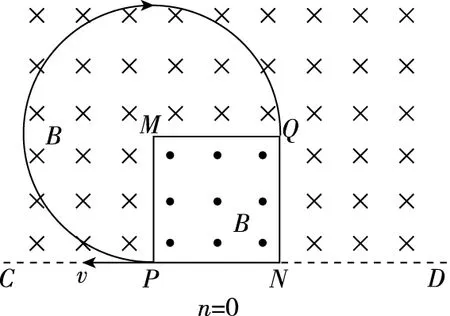
图3

【调研试题2】如图4所示，空间存在两个匀强磁场，其分界线是半径为R的圆，两侧的磁场方向相反且垂直于纸面，磁感应强度大小都为B。现有一质量为m、电荷量为q的带正电离子(不计重力)从A点沿OA方向射出。求：

(1)若向外的磁场范围足够大，离子自A点射出后在两个磁场中不断地飞进飞出，最后又能返回A点，求其返回A点对应离子速度的可能值。

(2)若向外的磁场是有界磁场，分布在以O点为圆心、半径为R和2R的两半圆之间的区域，上述离子仍从A点沿OA方向射出，且离子仍能返回A点，求离子返回A点的最大速度。(可能用到的三角函数值：sin37°=0.6，cos37°=0.8，tan72°=3.1，tan36°=0.73)

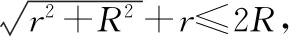
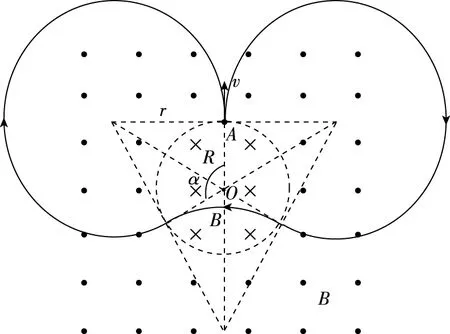
图5

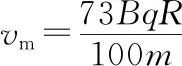
【技巧总结】带电粒子在半径为R的圆形磁场中的运动有几个重要的特点：

①在圆形磁场区域内，沿径向射入的粒子，必沿径向射出。

③对准圆心射入，速度越大，偏转角和圆心角都越小，运动时间越短。

④入射速度相同，运动半径相同时，弧长越长对应的时间越长。

⑤不沿径向射入的粒子，从磁场射出时，射入点和射出点连线的中点、磁场圆圆心、轨迹圆圆心在同一条直线上。

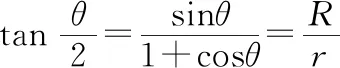
2.利用“归纳法”和“对称性”求解粒子在磁场中的运动时间

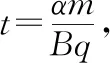
【调研试题3】如图6所示，直线MN下方无磁场，上方空间存在两个匀强磁场，其分界线是半径为R的半圆，两侧的磁场方向相反且垂直于纸面，磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出，最终打到Q点，不计微粒的重力。求：

图6

(1)微粒在磁场中运动的周期；

(2)从P点到Q点，微粒的运动时间。

【解题思路】(1)由微粒在磁场中的运动可知

(2)根据运动的周期性可知，带电粒子必须要经过两次穿越才能回到Q点，粒子的运动轨迹将磁场边界分成n等份(n=2，3，4……)，把n等分数段分奇偶各作出两个图，找出时间的通项式，如图7所示，观察n=2和n=4或n=3和n=5的运动轨迹，由对称性可以找出以下规律，即

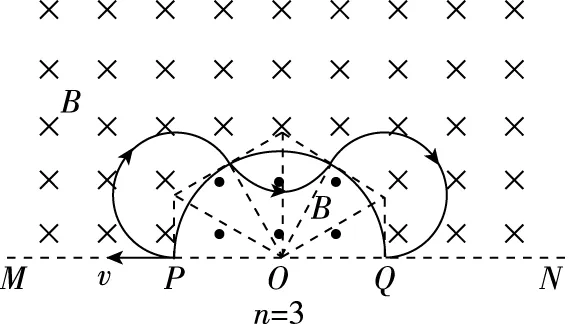
图7

①当n为偶数时，每一次穿越两个磁场，刚好是一个整圆，t为周期的整数倍，即

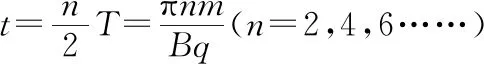
②当n为奇数时，每一次穿越两个磁场，刚好是一个整圆再多一个优弧，t为周期的整数倍加上最后一段的运动时间，即

【技巧总结】无论是求解速度还是时间，都应该以“等分法”入手，求速度时无需分奇偶讨论，而求带电粒子在磁场中的运动时间，一般都需要分奇偶来讨论不同的运动，用“归纳法”得出时间的通项公式，不管“嵌入型”磁场是什么几何形状，带电粒子运动是周期性大回旋还是部分回旋，该类问题都是通法通解。

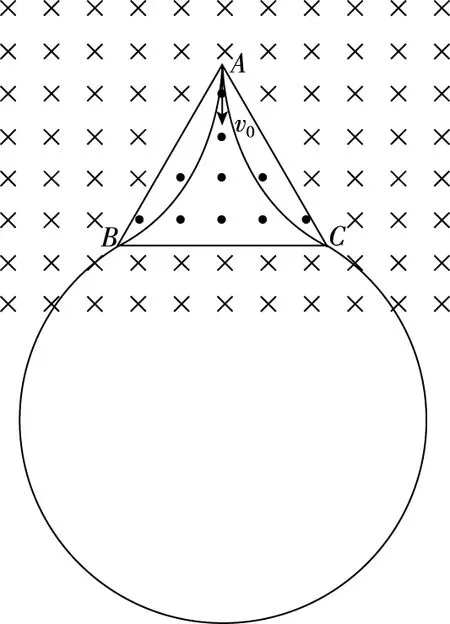
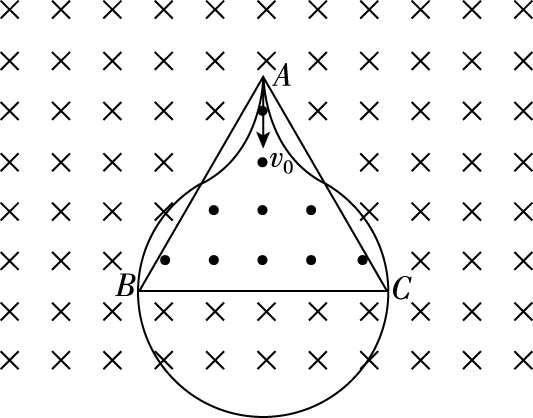
【调研试题4】如图8所示，边长为L的等边三角形ABC为两有界匀强磁场的理想边界，三角形内的磁场方向垂直纸面向外，磁感应强度大小为B，三角形外的磁场(足够大)方向垂直纸面向里，磁感应强度大小也为B。把粒子源放在顶点A处，它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计)。若从A射出的粒子

图8

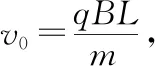
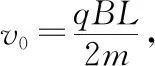
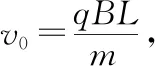
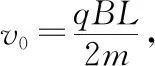
则下列判断正确的是

( )

A.t1=t3

C.t1

【解题思路】粒子在磁场中做匀速圆周运动，洛伦兹力提供粒子做圆周运动的向心力。

根据几何关系，作出运动轨迹r=L，如图9所示

图9

图10

【技巧总结】带电粒子只在洛伦兹力作用下做匀速圆周运动，由于多种原因会使问题形成多解，如带电粒子的电性不确定、磁场的方向不确定、初速度的方向不确定、临界状态不唯一、运动的周期性、初速度的大小不确定等等。带电粒子在“嵌入型”交变磁场运动是一个典型的多解问题，随着近几年高考试题的不断改革，试题更加趋于基础，所以这类问题常常改头换面以选择题的形式出现或转向考查最大速度、最大半径、最短运动时间，调研试题4以“嵌入型”交替磁场模型为背景，以选择题的形式出现，只考查把边界两等分，题目新颖，考向明确，难度不大，应引发关注，但万变不离其宗，关键还是要进行运动的可能性分析，养成规范作图的习惯，找出通解通法，才能以不变应万变。