理解天体运动知识 清除天体问题障碍
2020-11-13浙江成金德
浙江 成金德
人类对浩瀚的宇宙充满了各种梦想,随着科学技术的发展,探寻广袤宇宙的奥秘正在逐步实现。天体运动在力学中占有重要地位,要求学生熟练运用牛顿第二定律、万有引力定律、匀速圆周运动分析以及探讨天体的运动规律,解决此类问题学生需要对天体的运动构建模型,这对学生来说是一个难点。为解决此类难题,下面就有效复习天体运动的知识作以下探讨。
一、理解知识要点
1.三个要点
(1)一个定律
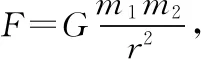
适用条件:严格地说公式只适用于质点间的相互作用,当两个物体间的距离远远大于物体本身的大小时,公式也可以近似使用,但此时r应为两物体重心间的距离。对于均匀的球体,r是两球心间的距离。
(2)一个模型
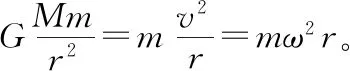
(3)一颗卫星
与地球自转同步,相对于地球表面静止的卫星,叫做同步卫星。其特点为六个“一定”:
①轨道平面一定。同步卫星绕地球旋转的轨道平面一定与地球的赤道面重合。
②周期一定。同步卫星的运行方向与地球自转方向一致,同步卫星的运行周期与地球的自转周期相同,即T=24 h。
2.三大关系
(1)天体的绕行速度、角速度和周期与半径的关系


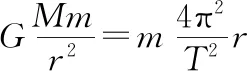
(2)运行速度、发射速度和宇宙速度间的关系
发射速度是指卫星随火箭一起上升过程结束后与火箭分离时的速度;运行速度是指卫星在空中绕地球正常运行时的速度;宇宙速度是三个特定的临界发射速度,如果以第一宇宙速度发射卫星时,卫星将绕地球表面运行。
宇宙速度是卫星做各种轨道运动的临界发射速度,它的数值是确定的;运行速度是各种各样的,随着轨道半径的增大而减小;发射速度取决于火箭发射系统,根据发射不同卫星的需要确定不同的发射速度。当以第一宇宙速度v=7.9 km/s发射时,恰好是卫星发射的最小速度,也是卫星环绕地球运行的最大速度。
(3)重力和万有引力的关系
地球对物体的吸引力就是万有引力,重力只是万有引力的一个分力,万有引力的另一个分力是物体随地球自转所需的向心力。


3.三项区分
(1)区分轨道半径和天体间的距离

(2)区分天上追及和地上追及
地面上的物体只要后者的速度大于前者的速度就可以追上。卫星间的追及不同于地面上物体的追及,在同一轨道上的两颗卫星,后者一旦加速,它将立即离开原轨道进入半经更大的高轨道上运动,因此,同一轨道上的卫星追及问题是一类典型的问题,实际采用的方法是先让追赶卫星减速,由半径大的高轨道转向半径小的低轨道,由万有引力的作用使卫星增大线速度,经一定时间后再使追赶卫星加速,由低轨道回到高轨道,这样才可以追上。
(3)区分赤道上物体、近地卫星和同步卫星
赤道上物体受到地球引力作用,此力的两个分力其中之一使物体随地球绕地轴转动,另外一个分力即为物体的重力;而近地卫星和同步卫星均受到地球的引力提供向心力,使它们绕地球转动。它们作圆周运动的半径关系为R物=R近 求解天体问题的基本思路是将天体的运动看作匀速圆周运动,中心天体的引力提供向心力,再结合天体表面处物体的重力大小等于天体对它的引力大小。 【例1】2008年9月25日,我国载人航天宇宙飞船“神舟七号”进入预定轨道,且中国人成功实现了太空行走,并顺利返回地面。我们通过电视转播画面看到航天员在出舱时好像“飘浮”在空中。 (1)试分析航天员“飘浮”起来的原因。 (2)已知地球的半径R,地面的重力加速度g,飞船距地面高h,航天员在舱外活动的时间为t,求这段时间内飞船走过的路程s。 【分析】(1)航天员随舱做匀速圆周运动,地球对航天员的万有引力提供向心力,航天员处于完全失重状态,故航天员“飘浮”起来。 (2)宇宙飞船绕地球做匀速圆周运动,地球对它的万有引力提供向心力,则有 设地球表面处有一物体,质量为m′,根据万有引力与重力间的关系可得 在时间t内,飞船做匀速圆周运动,则飞船走过的路程等于圆弧的长度,即 卫星绕地球运行时,随着轨道半径的增大,由万有引力提供向心力的关系可知,卫星的线速度减小,角速度减小,周期增大,向心力减小。 【例2】若人造卫星绕地球做匀速圆周运动,则下列说法正确的是 ( ) A.卫星的轨道半径越大,它的运行速度越小 B.卫星的轨道半径越大,它的运行角速度越小 C.卫星的轨道半径越大,它的运行周期越小 D.卫星的轨道半径越大,它的向心加速度越小 【分析】卫星绕地球做匀速圆周运动时,万有引力提供向心力,即 因此,可以判断当轨道半径增大时,运行速度减小,角速度减小,周期增大,向心加速度减小,故ABD正确,C错误。 卫星在轨期间自主改变运行轨道的过程称为变轨。卫星运行轨道是椭圆,当卫星处于远地点时,调整卫星所处状态后火箭点火,这样可使卫星的轨道变成需要的高度。若由高轨道变到低轨道时,则应调整好卫星状态并减速,使卫星靠近地球;随着卫星高度的降低,卫星的势能转变为动能,运行速度随之增大;若由低轨道变到高轨道时,则应调整卫星状态先加速,随着卫星高度升高,卫星的动能转变为势能,速度也会随之减小。当到达预定的轨道高度时,再次调整好卫星姿态并控制好速度,完成变轨操作。 【例3】如图1所示,搭载着“嫦娥二号”卫星的“长征三号丙”运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100 km、周期约为118 min的工作轨道,开始对月球进行探测 图1 ( ) A.卫星在轨道Ⅲ上的运行速度比月球的第一宇宙速度大 B.卫星在轨道Ⅰ上的机械能比在轨道Ⅱ上大 C.卫星在轨道Ⅲ上经过P点的速度比在轨道Ⅰ上经过P点时大 D.卫星在轨道Ⅲ上经过P点的加速度比在轨道Ⅰ上经过P点时大 地球同步卫星,即相对地球静止的卫星,其轨道平面只能与赤道平面重合,其轨道半径r、运行速度的大小v和运行周期T都是唯一确定的。求解同步卫星问题时,不仅要熟练应用万有引力提供向心力这个基本原理,还要注意应用同步卫星的有关特点。 【例4】某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,试问,春分那天(太阳光直射赤道)在日落12小时内有多长时间该观察者看不见此卫星?已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对光的折射。 在春分时,太阳光直射地球赤道,如图2所示,图中圆E表示赤道,S表示卫星,A表示观察者,O表示地心。从图中可看出,当卫星S绕地心O转到图示位置以后(设地球自转是沿图中的逆时针方向),其正下方的观察者将看不见它。考虑到对称性,有 图2 rsinθ=R 在天体运动中,把两颗彼此相距较近,而且绕同一点做圆周运动的恒星叫做双星系统。由于双星系统中两颗恒星绕它们连线上的某一固定点分别做匀速圆周运动,它们之间的万有引力提供各自所需的向心力,因此它们具有相同的角速度ω和相同的周期T。 【例5】现代观测表明,由于引力的作用,恒星有“聚集”的特点,众多的恒星组成不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星,它们以两者连线上的某点为圆心做匀速圆周运动,这样就不至于由于万有引力作用而吸引在一起,设某双星中A、B两星的质量分别为m和3m,两星间距为L,在相互间的万有引力的作用下,绕它们连线上的某点O转动,则O点距B星的距离是多大?它们运动的周期为多少?(引力常量为G) 【分析】设O点距B星的距离为x,双星运动的周期为T,由于相互间的万有引力提供各自所需的向心力,由牛顿第二定律和万有引力定律得 黑洞是太空里的某些区域,那里的引力大得惊人,包括光在内的一切东西都难以逃逸出来。由于光子逃不出黑洞对它的引力约束,则光子绕黑洞做圆周运动,它的轨道半径就是黑洞的最大可能半径。求解黑洞问题,要紧紧抓住这个要点建立方程。 【例6】1997年8月26日在日本举行的国际学术大会上,德国Max Planck学会的一个研究组宣布了他们的研究结果:银河系的中心可能存在一个大“黑洞”。所谓“黑洞”,它是某些天体的最后演变结果。 (1)根据长期观测发现,距离某“黑洞”6.0×1012m的另一个星体(设其质量为m)以2×106m/s的速度绕“黑洞”旋转,求该“黑洞”的质量M;(结果要求两位有效数字) 【分析】(1)设“黑洞”的质量为M,星体的质量为m,它们之间的距离为r,由于星体绕黑洞做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律得 解得黑洞的质量为 由此可得“黑洞”的可能最大半径为 卫星间的追及不同于地表上的追及,卫星间的追及问题是指两者从最近分离到再次相遇的问题。求解此类问题,关键是弄清低轨道卫星比高轨道卫星多运行一周时再次靠近的条件。 【例7】假设有一载人宇宙飞船在距地面高度为4 200 km的赤道上空绕地球做匀速圆周运动,地球半径约为6 400 km,地球同步卫星距地面高为36 000 km,宇宙飞船和一地球同步卫星绕地球同向运动,每当两者相距最近时。宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻两者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为多少? 【分析】设地球的质量为M,同步卫星的质量为m1,同步卫星的周期为T0,同步卫星离地球表面高度为h1,宇宙飞船的质量为m2,宇宙飞船的周期为T,宇宙飞船离地球表面高度为h2,由万有引力提供向心力可得 联立解得 设两者相邻两次相距最近的时间间隔为t2,有 天体问题往往可以与力学规律相联系,从而形成一类独特的综合问题,这类问题可以考查学生综合运用知识的能力。求解时既要注意应用天体问题的特点,还要注意灵活选用相关的力学规律。 【分析】设行星的质量为M,半径为R,宇宙站的质量为m,陨石的质量为m0。由万有引力提供向心力可得 对碰后的宇宙站和陨石有二、掌握解题方法
1.常规题型


2.运行情况
3.变轨问题

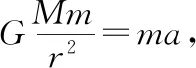
4.同步卫星
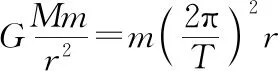

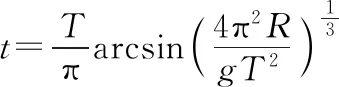
5.双星问题


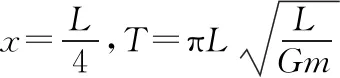
6.黑洞问题
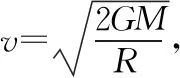
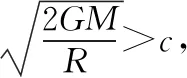
7.追及问题


8.综合运用力学规律



