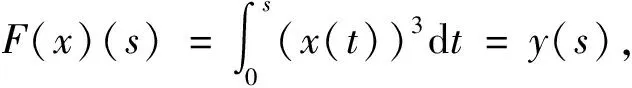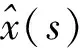求解第一类非线性积分方程的投影迭代法*
2020-11-12徐志海罗兴钧
徐志海,罗兴钧,张 荣
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
1 引言
第一类非线性算子方程F(x)=y的求解是典型的不适定问题,一般要用正则化方法[1-3],才能得到稳定的数值解.粗略的说,正则化方法分成两类:变分正则化方法与迭代正则化方法.Tikhonov正则化方法是典型的变分正则化方法[4],难点是极小化解的求解.因此实际问题广泛采用迭代正则化方法,比如Gauss-Newton方法[5-6]、Levenberg-Marquardt方法[7-8]、Landweber方法[9-10].由于Landweber 迭代方法,简单、容易实现,因此在实际问题中受到了广泛的关注.但是Landweber迭代方法对非线性算子F的要求比较苛刻,适用范围受限,因此,Scherzer在文献[11]中提出了求第一类非线性算子方程的改进的Landweber迭代方法.这个方法的优点是降低了对非线性算子F的要求,只要求F关于x的Frechet导数F′(x)满足Lipschitz条件,这个条件容易验证.由于Scherzer的方法是在无限维Hilbert空间中提出的,实际应用中无法实现,因此本文的主要工作就是在有限维空间中,提出离散的改进Landweber迭代算法,给出迭代停止准则,确保近似解的收敛性与收敛率.优点是实用性强,保收敛性.
2 离散的改进迭代格式
本节结合改进形式的Landweber迭代方法和多尺度Galerkin投影方法,给出求解第一类非线性积分算子方程的离散的改进迭代格式.
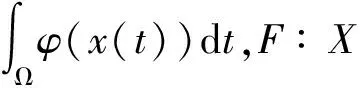
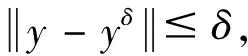
F(x)=yδ,
(1)
其中x是X中的未知元素,yδ是Y中的确定元素.
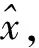
改进的Landweber迭代方法,其形式为
(2)
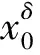
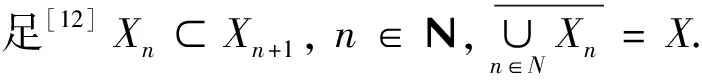
假定对于任意的n∈N,D(F)∩Xn≠φ,Pn∶X→Xn为正交投影算子.利用多尺度Galerkin投影方法离散改进的Landweber迭代方法(2),得到离散的改进Landweber迭代格式为
(3)
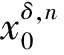
3 预先假设及迭代停止准则
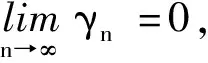
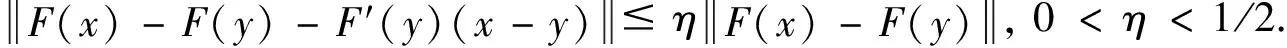
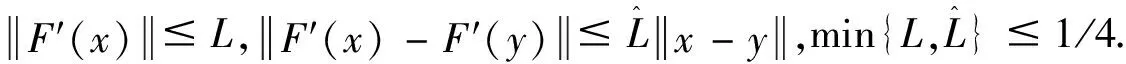
迭代停止准则(R1)
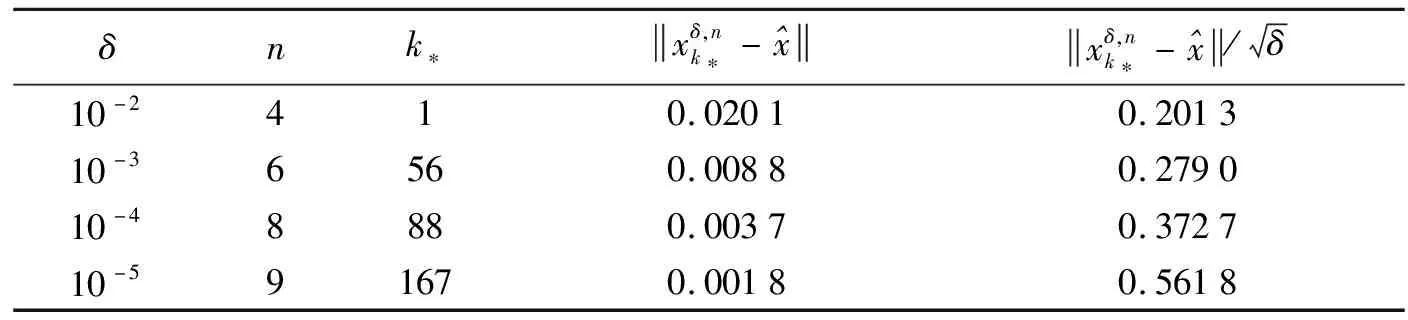
(i)选择整数n,满足γn (4) (5) (6) 由Cauchy-Schwarz不等式及(H3),有 (7) (8) (9) 注意到(I-Pn)2=(I-Pn),有 由(H1)、(H3),有 (10) 将(10)代入(9),有 (11) (12) 由(11),有 (13) 由(13)递推,有 现给出离散的改进迭代格式近似解的收敛率. (14) (15) 进一步有 (16) 由Cauchy-Schwarz不等式、(H4)、(16),有 (17) 以及 (18) 将(8)、(17)、(18)代入(5),有 (19) 由(14),有 (20) 由(15),有 容易验证F满足条件(H1)-(H3),假定yδ(s)=y(s)+δ·v(s),其中v(s)=sin(s),δ∶= 10-j,j=2,3,4,5.假定子空间Xn是在区间[0,1]中的节点j/2n上的分片线性多项式空间,其中j=0,1,2,…,2n-1.子空间Xn的子空间的正交直和空间分解关系式为Xn=X0⨁⊥W1⨁⊥…⨁⊥Wn,其中子空间X0是在区间[0,1]上的线性多项式空间.现选取子空间X0的一组正交基[11-12]为 子空间W1的一组正交基为 则子空间Wi的一组正交基可递归得到,即 数值结果见表1.表1中的数值结果是在选取τ=2.2,并利用迭代停止准则(R1)后验选取迭代次数k*.为了表明收敛速度与噪声水平和离散水平的关系,选取了不同的δ和n值.表1中数值结果与定理1的结论吻合,说明算法是有效的. 表1 数值结果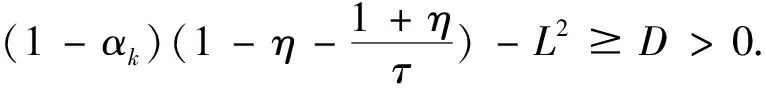
4 离散的改进迭代格式近似解的收敛性分析
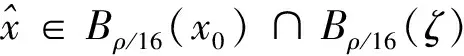
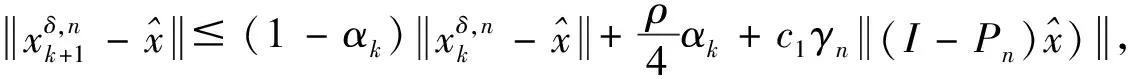
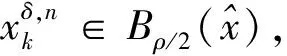
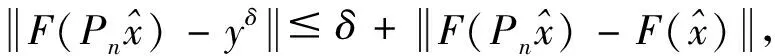
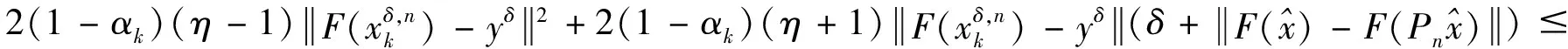
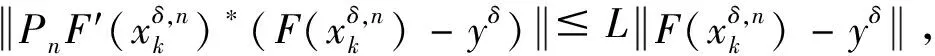
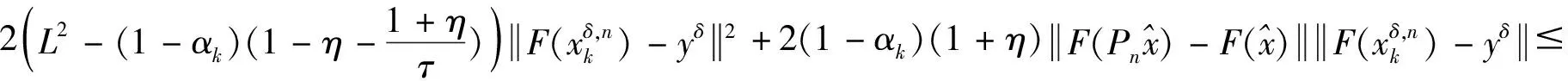
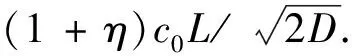
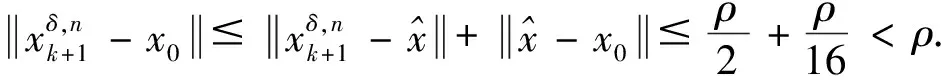
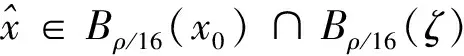
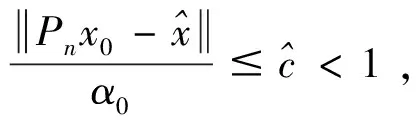
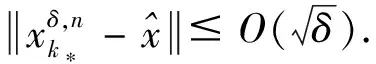
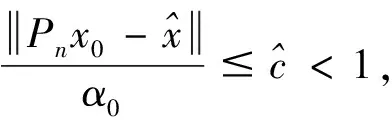
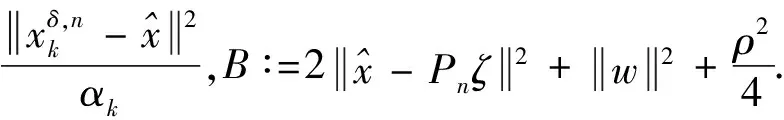
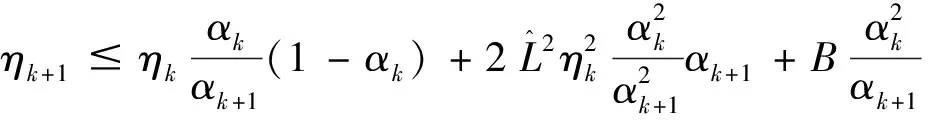
5 数值实验