单跨等截面柱门式刚架结构柱计算长度系数研究
2020-11-12段熙宾刘曹宇
段熙宾 刘曹宇
(中铁第一勘察设计院集团有限公司,西安710043)
0 引 言
门式刚架在城市公共建筑,如超级市场、购物中心、大型会展厅、生产车间等有普遍应用。对于门式刚架的静力性能,主要集中在门式刚架的极限稳定承载力和梁、柱的拼接节点上[1-5]。计算长度系数的研究源自于对轴心受压杆件的屈曲分析。Timoshenko[6]发表了著作《弹性稳定理论》。Julian 和Lawrence[7]依据子结构假定,提出了有侧移和无侧移框架结构柱计算长度的计算方法,并依此研究方法制出了尺解图。我国钢结构设计规范依据Julian 提出的单根框架柱计算长度系数的理想模型,制定了有侧移和无侧移框架柱子的计算长度系数表。该种研究方法假定同层的各个柱子具有相同的稳定参数,并且忽略了与计算柱子未直接相连构件对其产生的约束作用,所以导致其计算结果与实际受荷作用存在偏差,因而有许多学者对此研究方法进行了修正[8-9]。《门式刚架轻型房屋钢结构技术规程》和《冷弯薄壁型钢结构技术规范》则先后采纳了按层刚度计算的计算长度系数公式,以适用于各柱高度不等的刚架。梁启智和曾令付[10]进行了参数化研究,分析了山形门式刚架的整体稳定性,分别针对铰接和固接两种连接方式分析了山形门式刚架的梁柱临界应力和计算长度系数,并研究了计算长度系数随参数的变化趋势。李国强和侯和涛[11]提出了任意支撑作用下的钢框架柱的计算长度计算公式。目前,设计人员在对屋面板为钢骨架轻型板的门式刚架厂房进行设计时,采用何种规范仍存在争议。若采用《门式刚架轻型房屋钢结构技术规范》[12]对门式刚架厂房进行计算,经济效益极为显著,但给厂房结构的安全带来了一定的隐患;若采用《钢结构设计标准》[13]进行计算,刚架梁、柱的设计截面往往过大,且大多是由构件整体及局部稳定限值的构造要求控制,工程造价大幅增加,既不经济亦不合理。基于以上实际情况,结合西安动车检修段、大型养路机械检修段、大功率机车检修段等工程设计需求,有必要对此类采用钢骨架轻型板作屋面板的门式刚架结构的受力性能进行研究,得到该类结构的合理设计方法。
求解刚架柱的计算长度系数,需首先确定柱子两端的支座条件。由于梁柱连接节点既能承受一定的弯矩作用,又能够发生相对转动,在确定其支座条件时,不能简单地认为是铰接或者刚接连接,需要通过结构力学的计算,确定刚架结构对钢柱顶端的支撑刚度,即通过确定计算简图,求出其支座端的水平刚度与转动刚度。根据计算所得的支座刚度,在柱端设定水平弹簧支座和转动弹簧支座,再根据柱子屈曲存在微小弯曲变形的条件,建立刚架柱的平衡微分方程,以求解柱子的分岔屈曲荷载。在建立屈曲平衡方程时,本文做如下基本假定:
(1)构件是理想的等截面挺直杆;
(2)压力沿构件原来的轴线作用;
(3)材料符合胡克定律,即应力和应变呈线性关系;
(4)构件变形之前的平截面在弯曲变形之后仍为平面;
(5)构件的弯曲变形是微小的,曲率可以近似地用变形的二次微分表示,即Φ=-yʺ。
(6)不考虑门式刚架的整体失稳,仅对门式刚架单个杆件的稳定性进行研究。
由于柱脚连接方式的不同,直接会影响到刚架柱计算长度系数的计算结果,本文针对铰接、刚接两种柱脚连接方式展开研究,以确定两种情况下刚架柱计算长度系数的计算方法。
1 柱脚铰接刚架理论分析
对于柱脚铰接形式的刚架结构形式,可针对钢柱建立屈曲微分方程,柱子底部支座条件为铰接形式,顶部为水平弹簧支座和转动弹簧支座,所以在求解微分方程时,可认为柱子底端边界条件为柱位移和弯矩值为0,而柱子顶部有对平移的弹性约束及转动位移的弹性约束,即微分方程需满足剪力和弯矩平衡作为边界条件进行求解。柱脚铰接形式刚架柱计算简图如图1所示。
在求解水平弹簧支座和转动弹簧支座刚度时,可分别对两种弹簧支座形式作出计算简图,进行刚度求解。本文采用传统力学方法进行超静定结构的位移求解,可以求得单位位移下弹簧支座的反力值,即可得到转动弹簧支座刚度rB和水平弹簧刚度kB。水平位移计算简图如图2 所示,转动位移计算简图如图3所示。
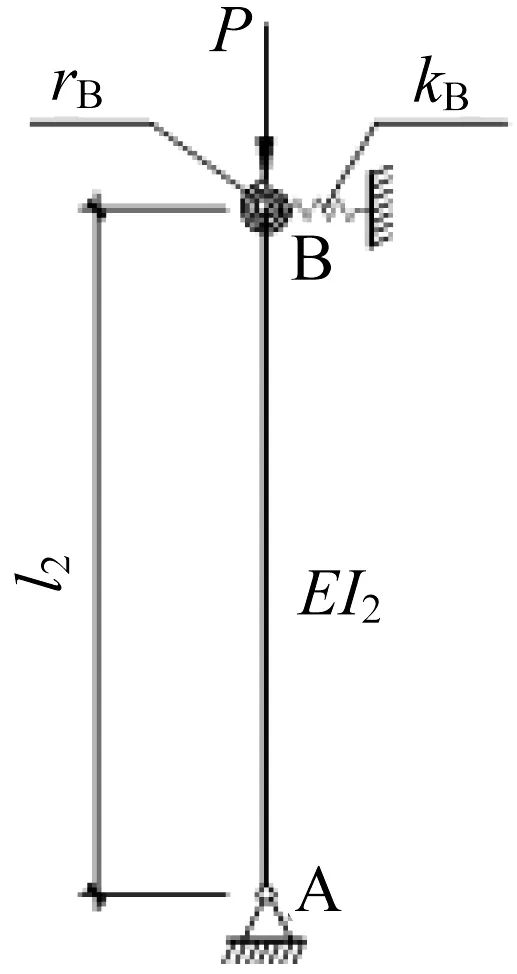
图1 柱脚铰接刚架柱计算简图Fig.1 Simplified calculation diagram of articulated rigid frame column
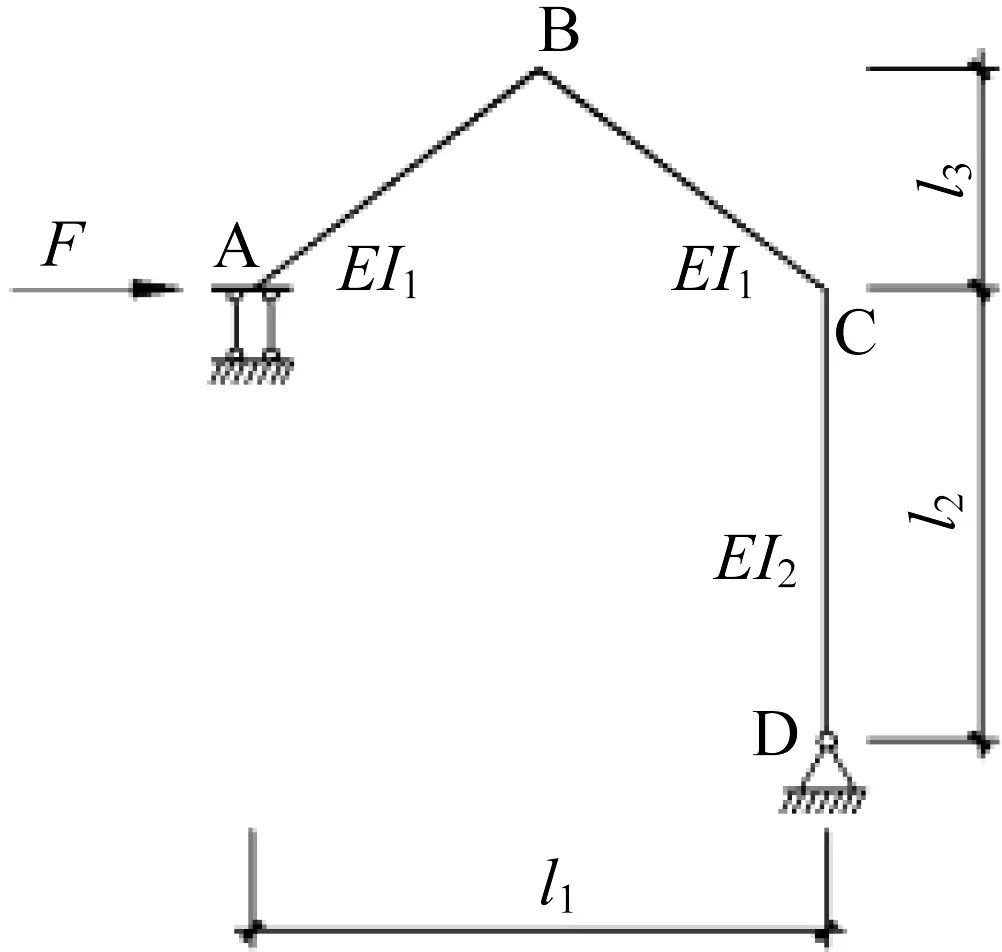
图2 水平弹簧支座位移计算简图Fig.2 Calculation diagram of displacement of horizontal spring bearing
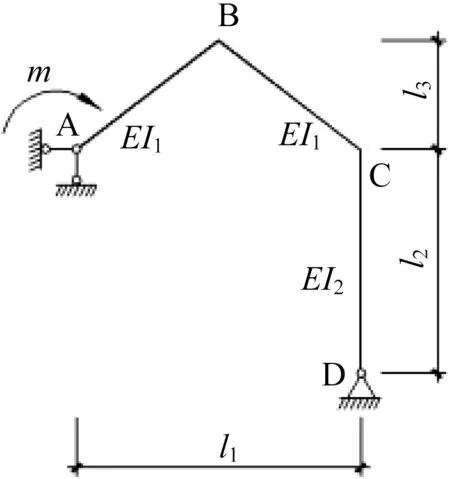
图3 转动弹簧支座位移计算简图Fig.3 Calculation diagram of displacement of rotating spring bearing
1.1 水平弹簧支座刚度计算
如图2 所示,水平弹簧支座位移计算简图为一次超静定结构,取A点力矩为多余约束力,撤去多余约束代之以未知力X1,得到如图4 所示的基本体系。
基本体系应满足A 点无转角位移的变形条件,力法方程为
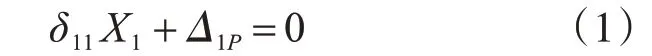
式中,δ11表示的是杆件在单位力X1的作用下,杆件端部产生的位移;Δ1P表示杆件在力F 的作用下,沿X1方向产生的位移。

图4 水平弹簧支座位移计算基本体系Fig.4 Basic system for calculating displacement of horizontal spring bearing
由于梁柱的线刚度为

当斜梁的长度越长,或斜梁坡度越大时,长度比例系数ξ值越大。
采用图乘法计算,可以得到柱脚铰接形式下刚架柱顶水平弹簧支座的刚度的计算公式:

1.2 转动弹簧支座刚度计算
如图3 所示,转动弹簧支座位移计算简图为一次超静定结构,取A 点水平约束力为多余约束力,撤去多余约束代之以未知力X1,得到如图5 所示基本体系。
采用图乘法计算,可以得到柱脚铰接形式下刚架柱顶转动弹簧支座的刚度的计算公式:
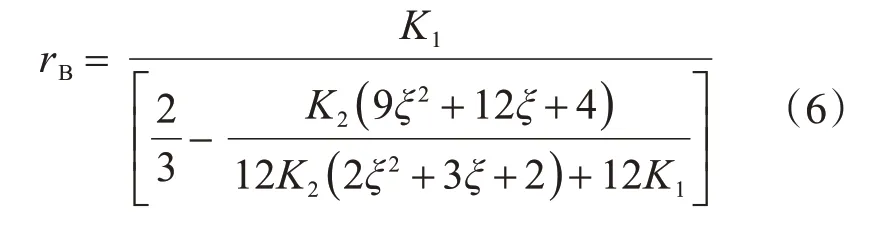
1.3 刚架柱的屈曲方程
如图1 所示,柱脚铰接形式刚架柱计算可简化为底部支座条件为铰接形式,顶部为水平弹簧支座和转动弹簧支座形式。在荷载P 作用下,刚架柱在其支座条件下发生变形,如图6 所示。其中,以顺时针的转角为正,向右的平移为正,柱端的力矩和水平力以与位移同方向时为正,异向时为负。
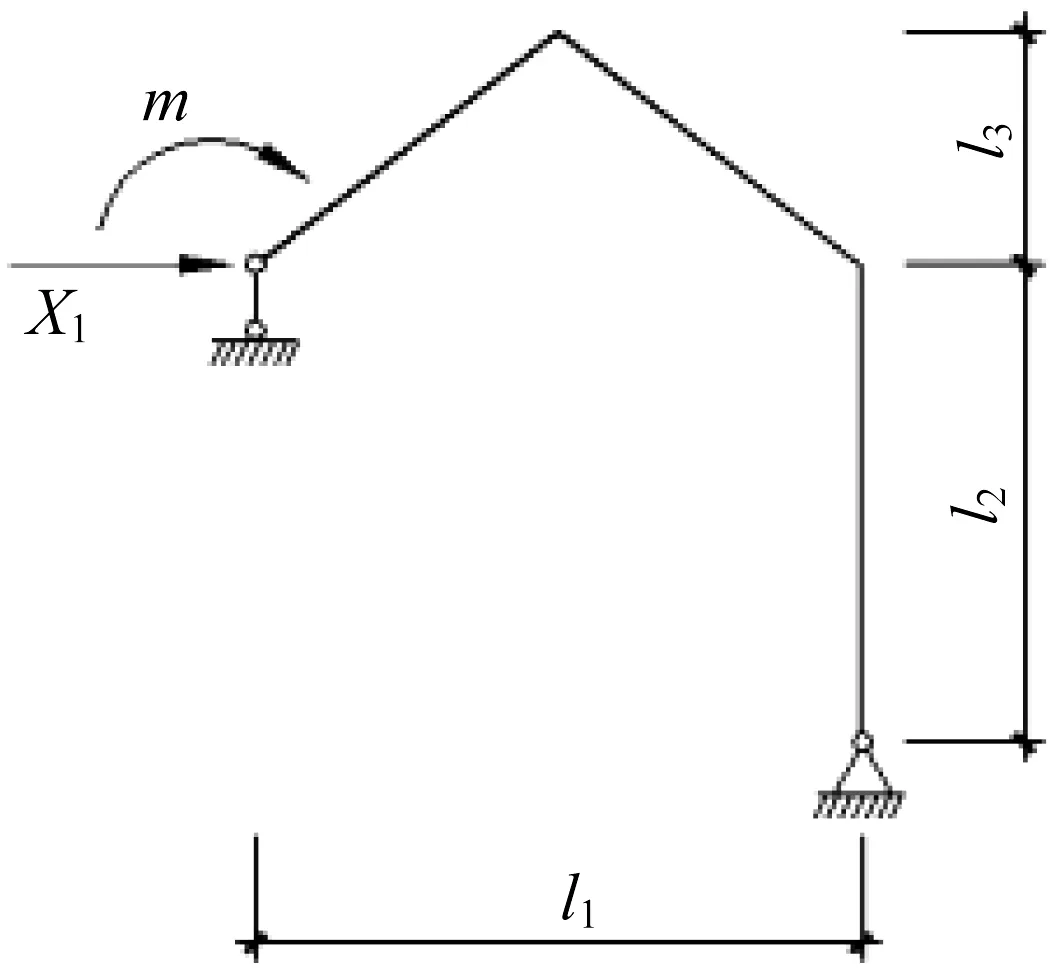
图5 转动弹簧支座位移计算基本体系Fig.5 Basic system for calculating displacement of rotating spring support

图6 刚架柱变形图Fig.6 Deformation diagram of rigid frame column
取如图7 所示隔离体,对单元隔离体建立弯矩平衡方程,得

建立力矩与x 轴相垂直的水平力的平衡方程:

将式(10)代入式(9),得:
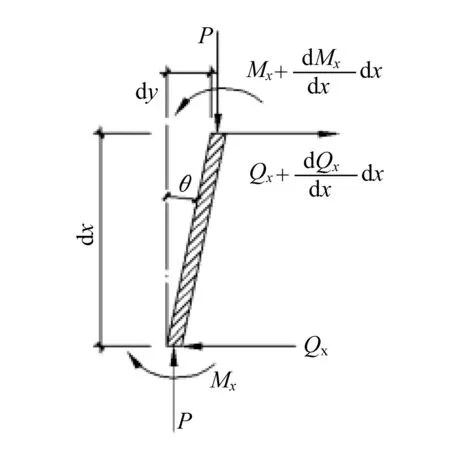
图7 单元隔离体Fig.7 Unit isolation body

由于式中各项参数具有如下关系:

将式(17)和式(18)代入式(13),得
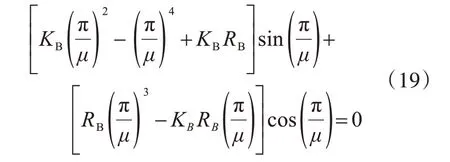
式(19)为柱脚铰接形式刚架柱的计算长度系数关于柱顶等效约束弹簧刚度的超越方程,当已知刚架结构的截面和刚架尺寸时,可根据式(5)和式(6)计算确定弹簧刚度值,继而通过式(19)求得柱子的计算长度系数μ。
1.4 数值拟合
由于式(19)是超越方程,本文采用割线法对方程实根进行迭代求解,令
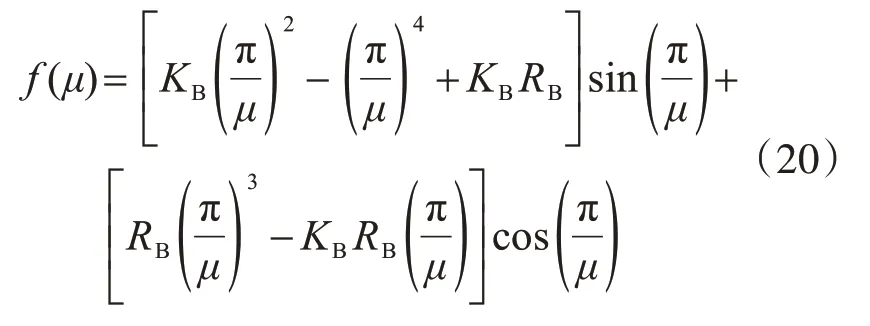
如图8 所示,方程与x 轴具有无数个交点,而求解柱子计算长度系数的目的是为了求出构件中性平衡状态时的最小荷载,故应求出计算长度系数μ值的最大解。
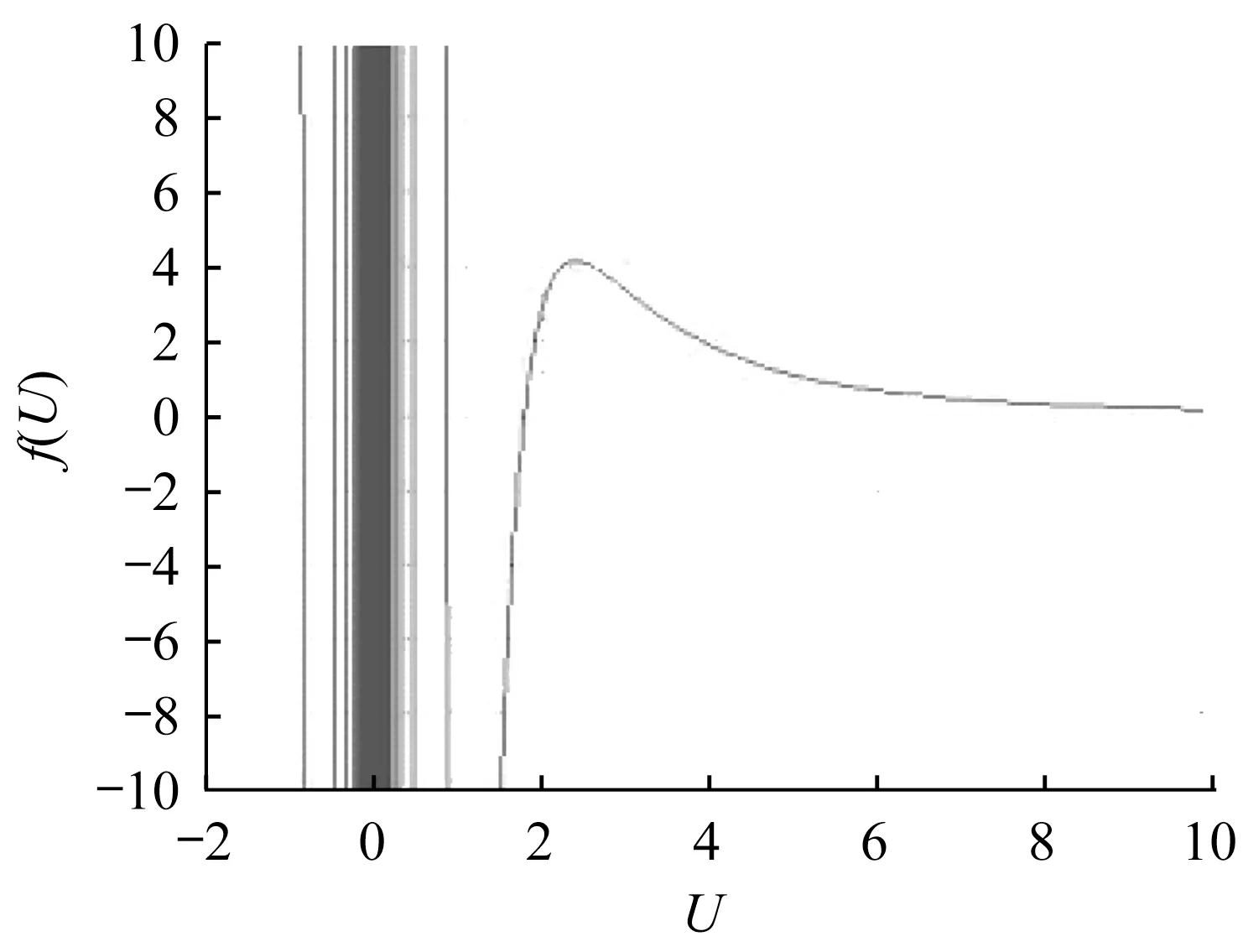
图8 超越方程示意图Fig.8 Diagram of transcendental equation
从0 至1 000 对KB、RB进行取值计算,可以得到计算长度系数取值,根据μ值变化速率,可制得柱脚铰接刚架柱计算长度系数取值表,见表1。
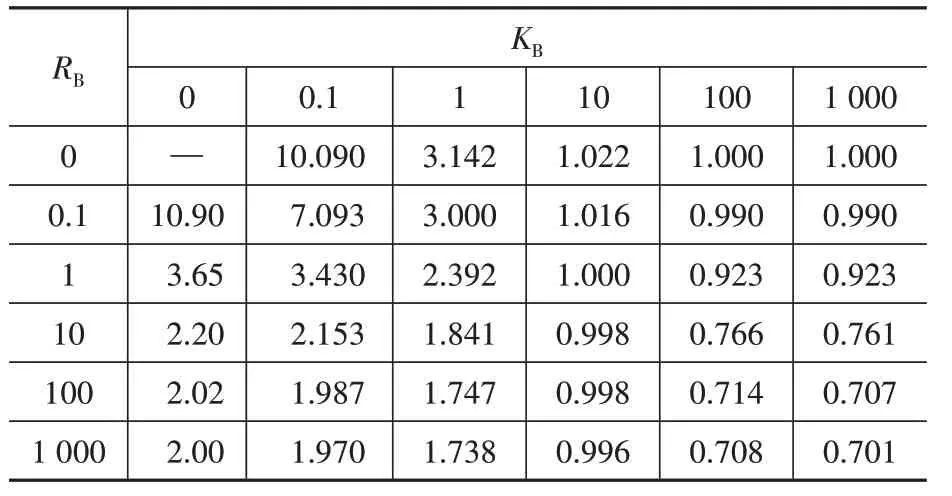
表1 柱脚铰接刚架柱计算长度系数取值Table 1 Values of length coefficient of column hinged frame column at column foot
当水平弹簧刚度取值为0,转动刚度取值为1 000 时,μ 值计算结果为2.002,此时可以认为刚架柱简化为柱脚铰接,顶部平移但不能转动的理论模型,接近于理论模型中μ 值为2.0 的计算结果;当水平弹簧刚度取值为1 000,转动刚度取值为0时,μ 值计算结果为1.0,此时可以认为刚架柱简化为两端铰接的理论模型,等于理论模型中μ值为1.0 的计算结果;当水平弹簧刚度取值为1 000,转动刚度取值为1 000 时,μ 值计算结果为0.701,此时可以认为刚架柱简化为柱脚铰接,顶部刚接的理论模型,接近于理论模型中μ 值为0.7的计算结果。
对计算μ 值的超越方程进行拟合,需先确定超越方程的曲面形式,将KB、RB从0 至100 的计算结果绘制成曲面,如图9所示。

图9 柱脚铰接刚架柱计算系数变化曲面图Fig.9 Calculation of coefficient variation surface diagram of column hinged frame column
由表1 及图9 可以发现,当KB、RB趋向于无穷大时,函数趋向于定值。使用MATLAB 对计算数据进行数值拟合,可以得到各项参数的系数值。即柱脚铰接形式刚架柱计算系数拟合公式为

拟合公式和超越方程计算数据对比如图10所示,其中,散点代表超越方程计算结果,三维曲面云图代表拟合公式计算结果。

图10 拟合公式和超越方程计算数据对比图Fig.10 Comparison of the calculated data of the fitting formula and transcendental equation
计算可得,拟合公式(21)的确定系数为0.987 9,标准差为0.111 5,且计算结果略大于超越方程计算结果,所以拟合公式计算足够精确,且可以适用于实际工程计算取值。
2 柱脚刚接刚架理论分析
对于柱脚刚接的刚架结构形式,可针对钢柱建立屈曲微分方程,柱子底部支座条件为刚接形式,顶部为水平弹簧支座和转动弹簧支座,在求解微分方程时,认为柱子底端边界条件为柱位移和转角为0,而柱子顶部有平移的弹性约束及转动的弹性约束,即微分方程需满足剪力和弯矩平衡作为边界条件进行求解。柱脚铰接形式刚架柱计算简图如图11所示。
2.1 水平弹簧支座刚度计算
与前述计算过程类似,采用图乘法计算,可以得到柱脚刚接形式下刚架柱顶水平弹簧支座的刚度的计算公式:

图11 柱脚刚接形式刚架柱计算简图Fig.11 The calculation diagram of rigid frame column with rigid joint form
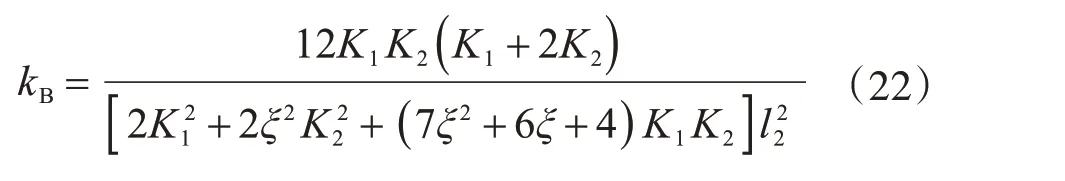
2.2 转动弹簧支座刚度计算
与前述计算过程类似,采用图乘法计算,可以得到柱脚刚接形式下刚架柱顶转动弹簧支座的刚度的计算公式:
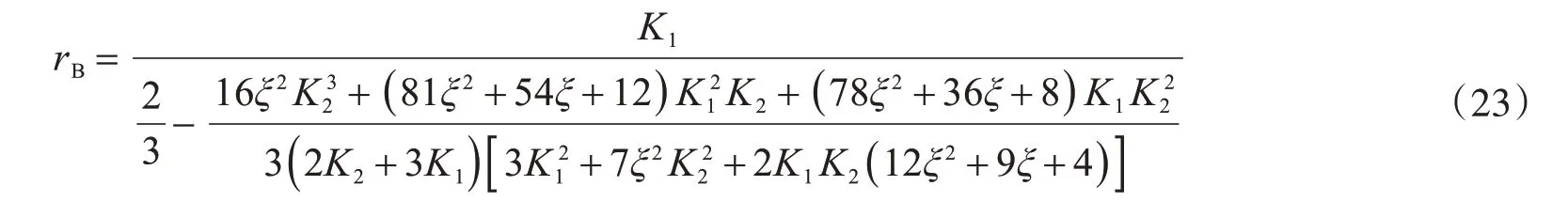
2.3 刚架柱的屈曲方程
如图11 所示,柱脚刚接刚架柱计算可简化为底部支座为刚接形式,顶部为水平弹簧支座和转动弹簧支座形式。在荷载P 作用下,刚架柱在其支座条件下发生变形,如图12所示。

图12 刚架柱变形图Fig.12 Deformation diagram of rigid frame column
与建立柱脚铰接形式下刚架柱屈曲方程方法相同,取如图13所示隔离体。
建立柱脚刚接形式下刚架柱屈曲方程:
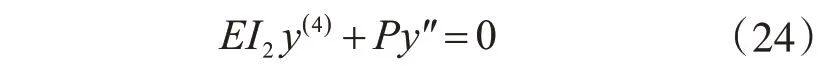
令k2=P/EI2,可得到微分方程的通解:
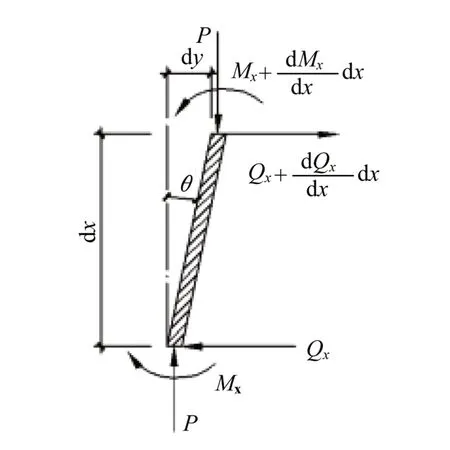
图13 单元隔离体Fig.13 Unit isolation body
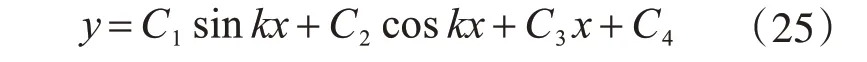
方程的边界条件为y(0)=0 和y'(0)=0。与前述推导过程类似,求解方程可得柱脚刚接形式下刚架柱的计算长度系数关于弹簧刚度的超越方程:

在确定弹簧刚度值时,即在确定刚架的截面大小和刚架尺寸时,可根据式(22)和式(23)计算确定弹簧刚度值,继而求得柱子的计算长度系数。
2.4 数值拟合
同样采用割线法对方程式(26)的实根进行迭代求解。令
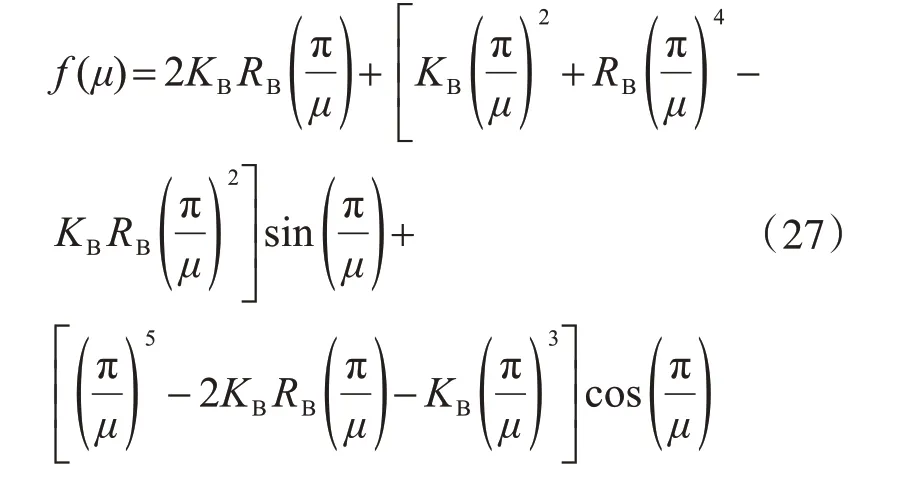
如图14所示,方程与x轴具有无数个交点,需求出计算长度系数μ值的最大解。
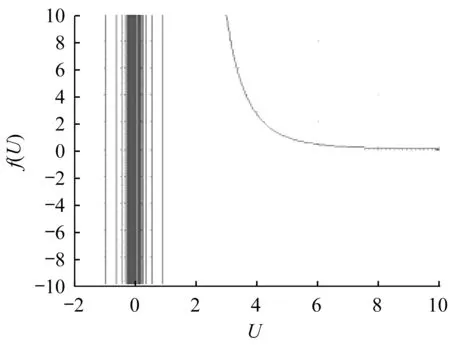
图14 超越方程示意图Fig.14 Diagram of transcendental equation
从0 至1 000 对KB、RB进行取值计算,可以得到计算长度系数取值,根据μ值变化速率,可制得柱脚刚接刚架柱计算长度系数取值表,见表2。
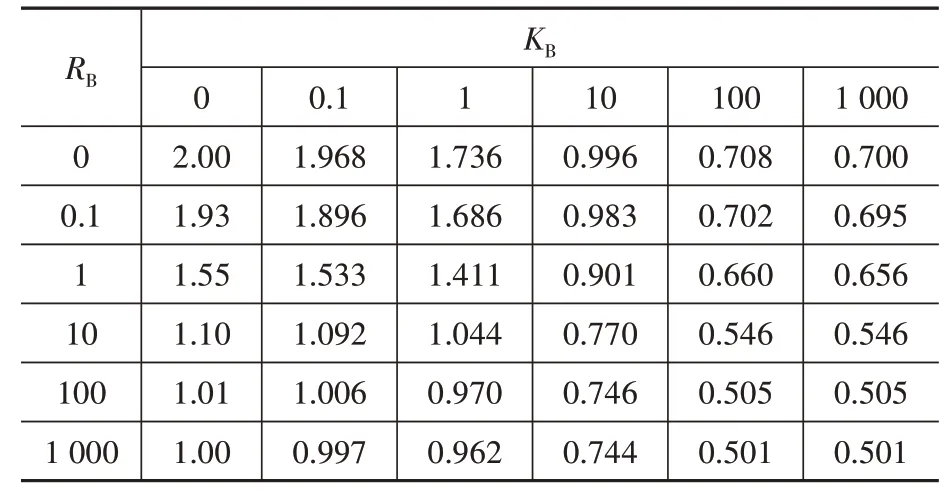
表2 柱脚刚接刚架柱计算长度系数取值Table 2 Values of length coefficient of column leg rigidness frame column
当水平弹簧刚度取值为1 000,转动刚度取值为0时,μ 值计算结果为0.7,此时可以认为刚架柱简化为柱脚刚接,顶部铰接的理论模型,等于理论模型中μ 值为0.7的计算结果;当水平弹簧刚度取值为0,转动刚度取值为0 时,μ 值计算结果为2,此时可以认为刚架柱简化为柱脚刚接,顶部自由的理论模型,等于理论模型中μ 值为2 的计算结果;当水平弹簧刚度取值为1 000,转动刚度取值为1 000 时,μ 值计算结果为0.501,此时可以认为刚架柱简化为两端刚接的理论模型,等于理论模型中μ值为0.5的计算结果。
对计算μ 值的超越方程进行拟合,需先确定超越方程的曲面形式,将KB、RB从0 至100 的计算结果绘制成曲面,如图15所示。
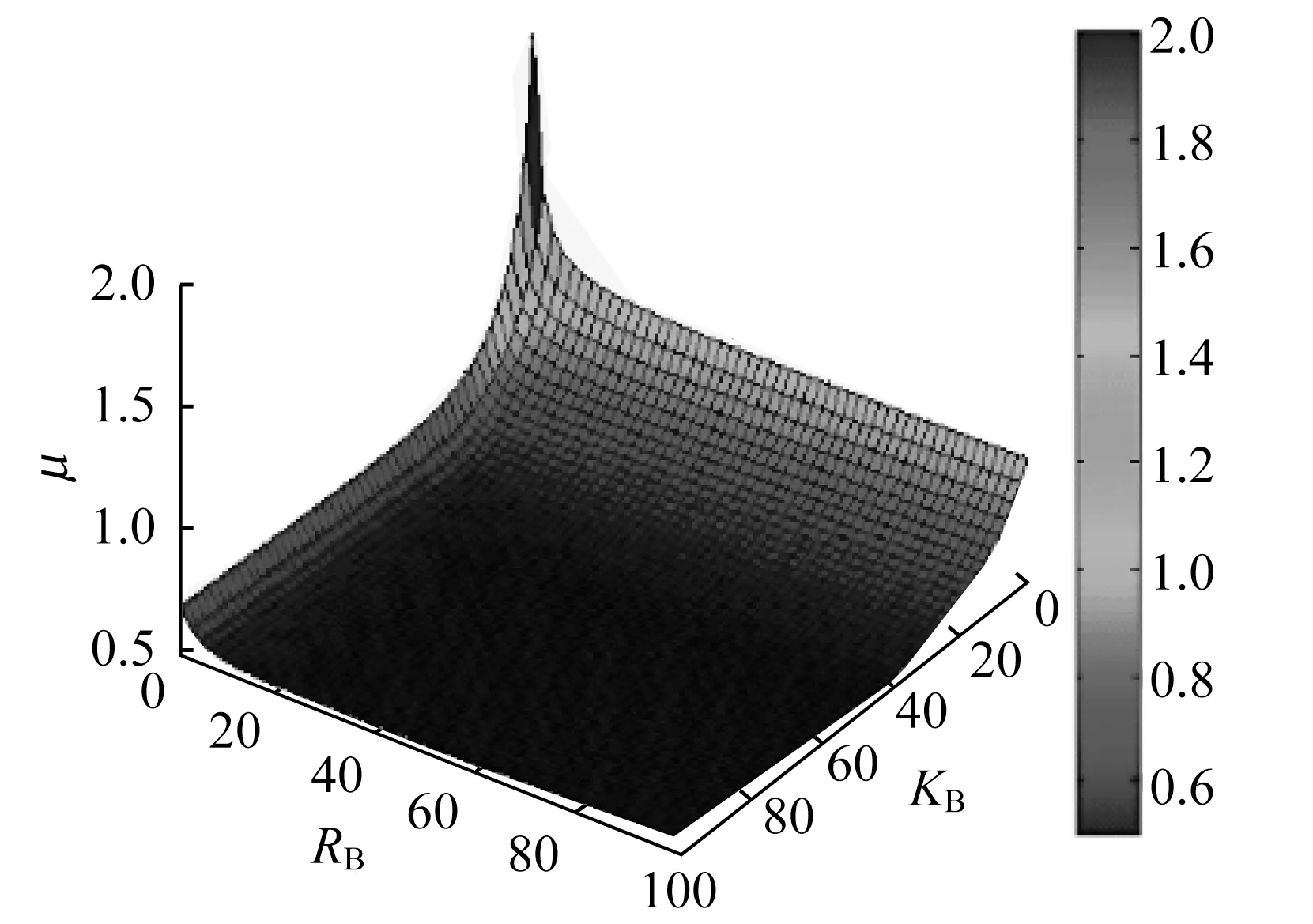
图15 柱脚刚接刚架柱计算系数变化曲面Fig.15 Calculation of coefficient variation surface diagram of column leg rigid-frame column
由表2 及图15 可以发现,当KB、RB趋向于无穷大时,函数应趋向于定值。使用MATLAB 对计算数据进行数值拟合,可以得到柱脚刚接形式下刚架柱计算系数拟合公式为
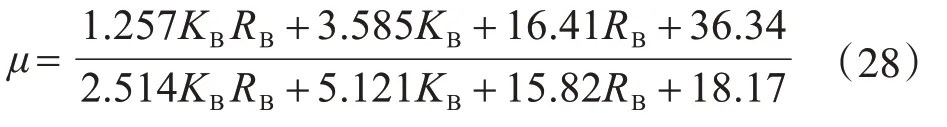
拟合公式和超越方程计算数据对比如图16所示,其中,散点代表超越方程计算结果,三维曲面云图代表拟合公式计算结果。
计算可得,拟合公式(28)的确定系数为0.977 5,标准差为0.048 18,计算结果略大于超越方程计算结果,所以拟合公式计算足够精确,且可以适用于实际工程计算取值。
3 结 论
(1)对两种柱脚连接形式下单跨门式刚架等截面刚架柱顶部等效约束刚度做了理论推导与分析,提出了约束刚度的计算公式,其水平支撑刚度同梁柱线刚度比、梁柱长度比值级钢柱几何长度有关,转动支撑刚度同梁柱线刚度比、梁柱长度比值有关。利用该公式,根据刚架尺寸及截面等基本信息可快速计算出柱顶部约束刚度值。
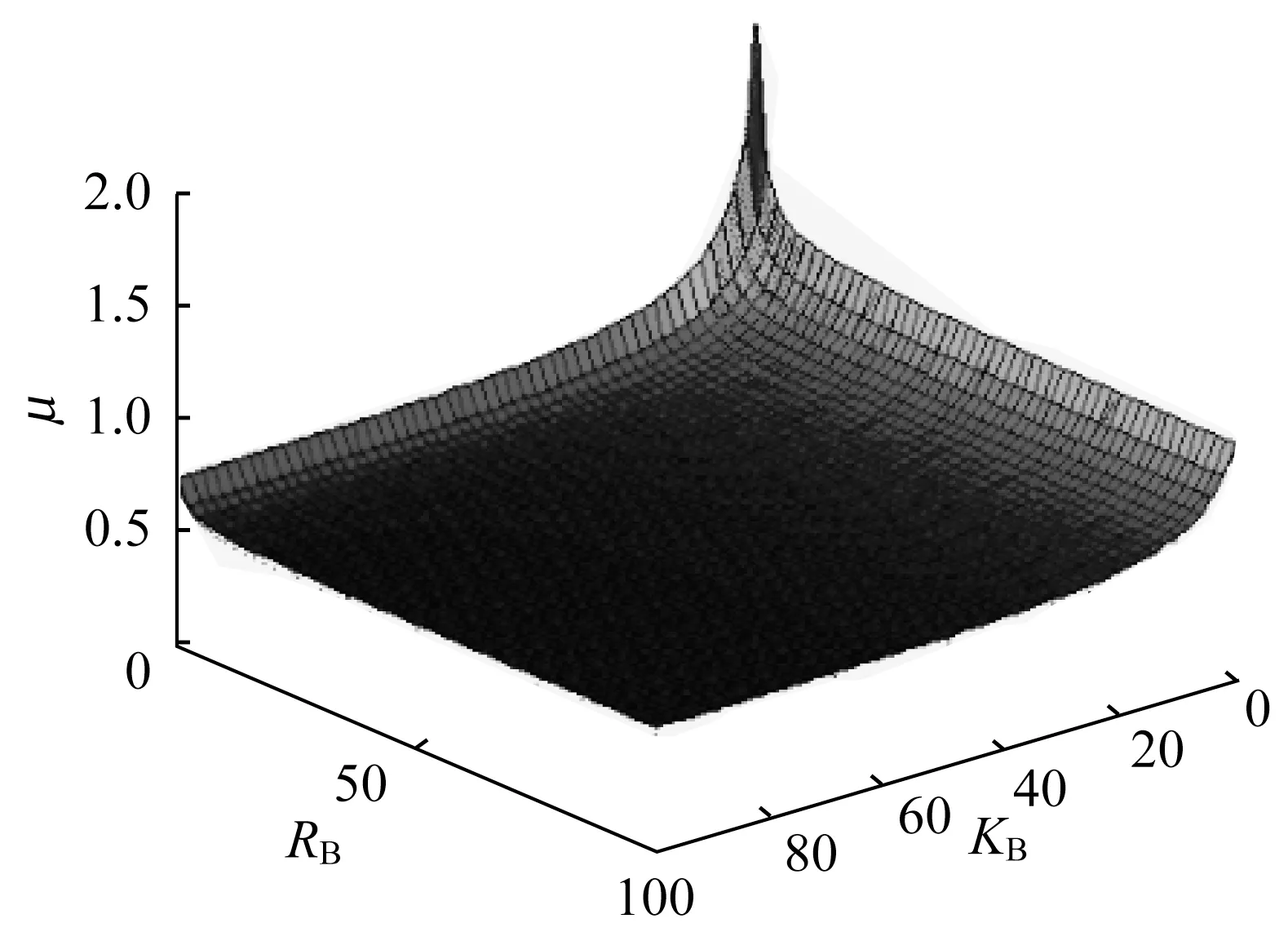
图16 拟合公式和超越方程计算数据对比图Fig.16 Comparison of the calculated data of the fitting formula and transcendental equation
(2)通过建立铰接柱脚及刚接柱脚的刚架柱屈曲微分方程,推导出关于响应的刚架柱平面内计算长度的超越方程,并得到计算长度系数的拟合计算公式,该公式具有较为精确的近似结果。
