基于遗传算法的三角挂篮设计参数的优化分析
2020-11-12郭增伟向中富
程 皓 郭增伟 向中富
(重庆交通大学土木工程学院,重庆400074)
0 引 言
20世纪60年代,德国在战后重建过程中利用挂篮成功实现了混凝土梁桥的无支架平衡悬臂浇筑施工,这种方法一般将混凝土梁体划分成2.0~5.0 m 一个节段,以挂篮作为现浇混凝土梁段的临时支撑结构。经过几十年的发展,悬臂浇筑用挂篮已逐渐成为定型的系列产品并成熟应用于各类悬臂浇筑梁桥的施工中[1]。我国城市化的进程造成了城市交通量的迅猛增加,城市新建桥梁的宽度也越来越大,如几江大桥桥面总宽34 m[2]、超级工程港珠澳大桥宽33.1 m[3]、郭家沱长江大桥上层桥宽达39 m[4]。混凝土箱梁桥宽度的增加必然导致悬臂浇筑用的挂篮宽度、承载能力的增加,传统的、成熟的定型挂篮可能无法满足超宽箱梁的现浇施工,超宽、超大承载力挂篮的研制也逐渐成为城市梁桥悬臂浇筑施工中必须要面对和解决的关键问题之一。
目前国内对于宽幅桥的挂篮优化设计已开展了一些研究和工程实践,张洪斌[5]指出目前挂篮的强度设计偏于保守,挂篮设计优化空间较大;吴月星[6]对挂篮后锚杆件的数目和位置进行了优化,使挂篮的经济性更好并且拱圈节段受力更均匀;龙兵[7]为了平衡桥面横坡的高差,将三角挂篮改造为异形挂篮,并对斜杆与水平方向的夹角、上下横梁的设计进行了优化,较好地解决了宽箱梁下横梁挠度过大的问题;张建国[8]对挂篮分系统、分构件、分工况进行优化分析使各构件满足受力要求,设计了上横梁的“马鞍”结构,有效地降低了主桁架高度并节约了成本;肖向荣[9]为改善前支点挂篮局部受力,提出了接长杆体内轨道式滑轨、锚固型止推器、倒三角绕轴旋转反顶轮等新构造。目前挂篮优化分析的方法大多依托某一实际工程,对挂篮的某一项参数进行单独分析,或是对挂篮某几个部分进行特殊设计以达到优化设计的目的,研究结果的个性、针对性太强,且主要集中在挂篮的安全性验算上,没有考虑挂篮主桁的安全性与经济性之间的博弈,另外关于挂篮主桁架最主要的几个设计参数(立柱高、构件截面形式)之间的取值与组合问题的研究成果也相对较少。
本文以三角挂篮为对象,以挂篮最大变形和最大应力需满足JTGT-F50—2011《公路桥涵施工技术规范》[10]要求为约束条件,以挂篮用钢量为目标函数建立三角挂篮的数学优化模型,在保证挂篮受力性能满足规范要求的前提下提高了主桁架的经济性,为三角挂篮的设计及优化提供了数学建模的方法,以重庆高家花园大桥复线桥为工程背景,使用遗传算法求解了悬臂浇筑用挂篮的设计参数,并通过Midas/civil 的数值计算验证了模型的正确性。
1 三角挂篮及其设计参数优化模型
1.1 三角挂篮结构及传力路径介绍
三角挂篮主要由如图1 所示的承重系统(三角主桁)、锚固系统(后锚梁、下锚梁)、悬吊系统(吊带)、行走系统(轨道、内外滑梁)、模板系统及作业平台等几部分组成。新浇筑、还未形成强度的混凝土箱体重量依次经下纵梁、下横梁、钢吊带传至三角主桁,并通过挂篮的前、后支点将荷载最终传递给已浇梁段。下纵梁、下横梁均匀地分散在挂篮下部,主要起到分散荷载的作用,工作应力相对较小也不会显著影响挂篮的整体刚度,而三角主桁和钢吊带工作应力水平较高,对挂篮整体刚度的影响较大。
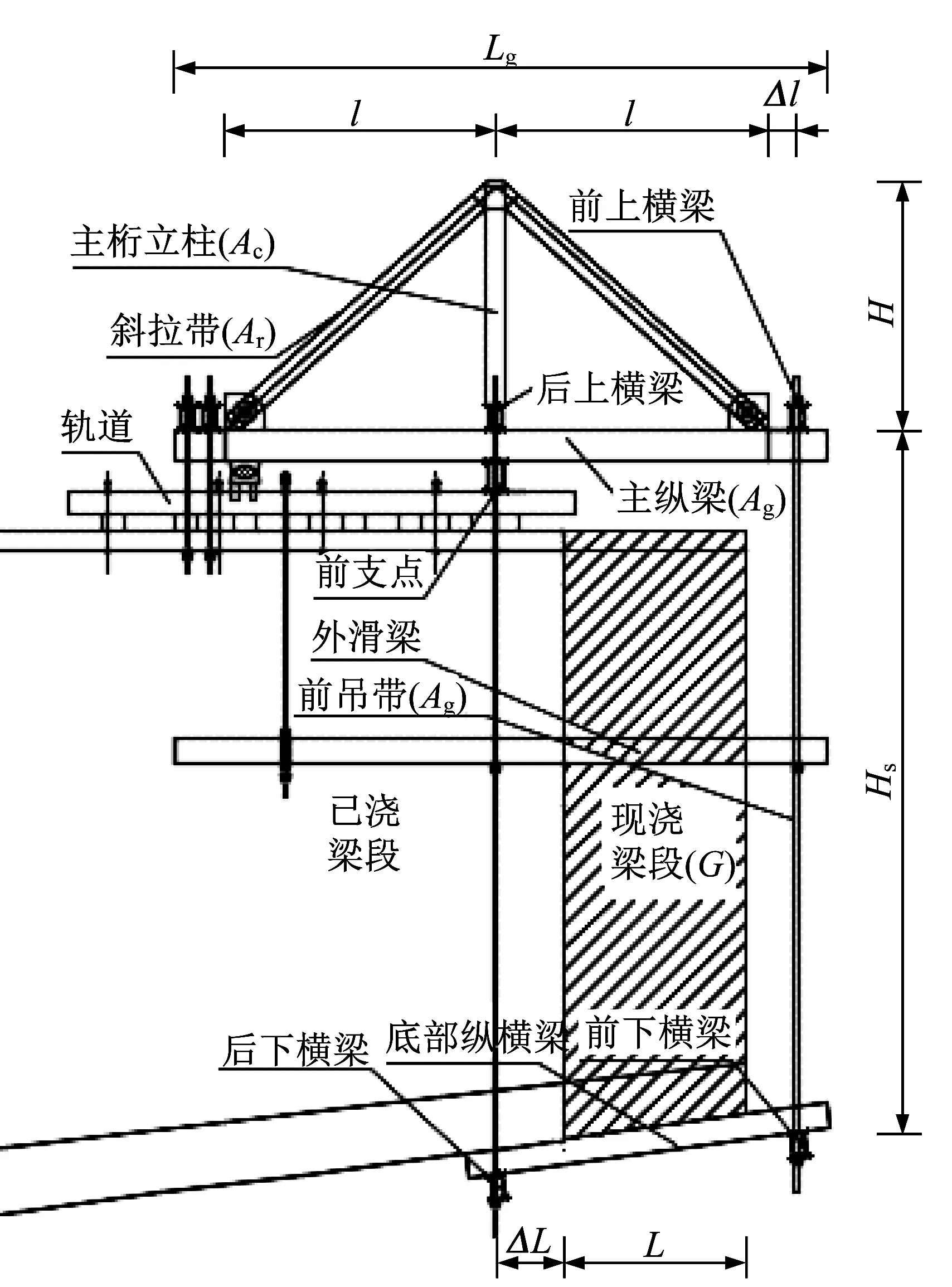
图1 三角挂篮示意图Fig.1 Diagram of triangle form traveler
式中:L 为最不利工况箱梁的节段长;G 为最不利工况箱梁的重量;H 为立柱高度;Hs为前吊带的长度(由最不利工况箱梁的高度确定);Lg为主纵梁长度;l为主纵梁和斜拉带交点与后上横梁之间的水平距离;Δl 为主纵梁和斜拉带前交点与前上横梁之间的水平距离;ΔL为挂篮下支点与箱梁后端之间的水平距离。
1.2 挂篮设计参数优化模型
为保证挂篮结构的安全性和良好的使用性能,CJJ/T 281—2018《桥梁悬臂浇筑施工技术标准》[11]要求挂篮结构的整体变形不超过20 mm,Q235b钢材制作的主桁架结构最大应力不得超过190 MPa,钢吊带要满足2 倍安全系数。主桁、吊带的数量和截面尺寸的增加会减小挂篮的工作应力和变形,提高挂篮结构的安全性,但这必然导致挂篮用钢量的增加,挂篮制造费和措施费也将显著增加。如何在保证结构安全的前提下尽量减小用钢量以节省挂篮制造费成为挂篮设计过程必须解决的主要矛盾。
考虑到主桁高度、主桁和吊带截面尺寸是影响挂篮安全性和使用性能的主要因素,建立挂篮参数优化模型时,假定挂篮各榀主桁架构造参数完全相同,并选取主桁架立柱的高度H、截面积Ac、纵梁截面积Ag、斜拉带截面积Ar和吊带总截面面积As为待优化参数,定义挂篮用钢量Sc为目标函数:
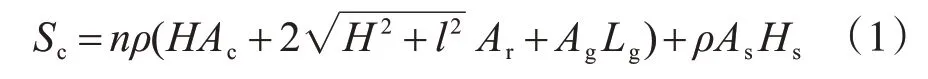
式中:n 为主桁架榀数(由箱梁腹板的位置和数目确定);ρ为Q235b钢的密度。
为保证挂篮结构的安全,需要限制挂篮的工作应力和变形,参考CJJ/T 281—2018《桥梁悬臂浇筑施工技术标准》中的规定,设置主桁最大应力值σmax≤190 MPa、PSB830 精轧螺纹钢吊带应力值σs≤415 MPa、挂篮总变形Δ≤20 mm 三项约束条件。另外,为了确保挂篮受压构件的稳定性,参考《结构稳定理论》[12],设置轴心受压构件立柱的轴力值Nc≤Pcr。同时根据工程实际需求,精轧螺纹钢的公称直径取值范围为18~50 mm,可以据此限制As的取值范围。

式中:Nc、Ng、Ns分别为主桁立柱、纵梁和吊带轴向力;Wg为主纵梁抗弯截面系数;Pcr为立柱的欧拉临界力;Δt为主桁变形量;ns为前吊带根数(由箱梁宽度确定);φmin为精轧螺纹钢的最小公称直径0.018 m;φmax为精轧螺纹钢的最大公称直径0.050 m。
1.3 挂篮设计参数优化模型中参数求解
挂篮设计参数的优化求解首先需要将优化模型的约束条件表达为待优化参数的函数,参照图1 的三角挂篮结构,把梁段自重简化为作用于梁段质心的集中荷载G,按照杠杆原理可以计算出前吊带的总轴力Ns,假设三角挂篮各榀主桁架均匀分担梁段自重,则前吊带传递至单榀主桁架的竖向力为
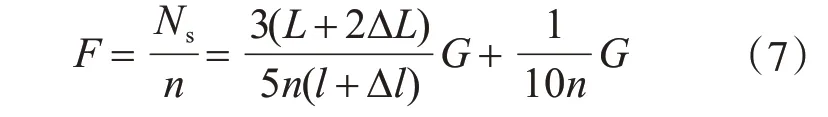
求得吊带传递给单榀主桁架的竖向力后,三角挂篮主桁架的受力模型即转化为如图2(a)所示的一次超静定平面杆系结构,使用如图2(b)所示的基本结构,利用变形协调条件建立主桁架斜拉杆的力法方程,求解后即可得到斜拉杆ad 的轴力Nr:
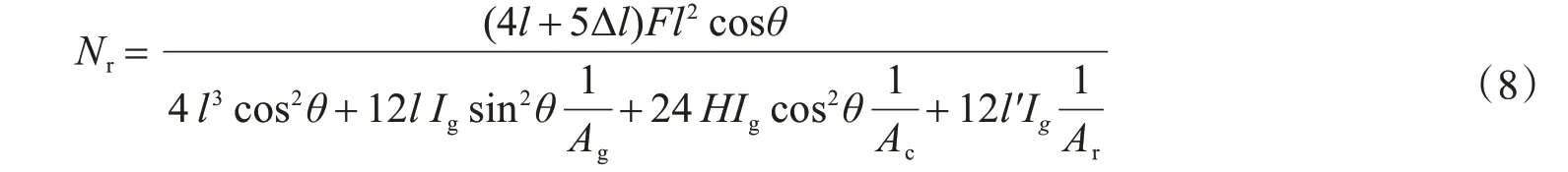
式中,Ig为挂篮主纵梁截面惯性矩;θ=arctan(l H)。
当Nr的竖向分量小于F 时,纵梁最大弯矩位于主纵梁与立柱的交界位置,大小为F(l+Δl)-Nrlcosθ。反之,主纵梁最大弯矩值在主纵梁与右斜拉带的交界位置,大小为FΔl。三角挂篮结构的截面形式多采用方管和双拼槽钢,可以将双拼槽钢简化为方钢管并假定方钢管壁厚为其边长b的η 倍,则通过截面特性的推导可以将方钢管的抗弯截面系数W、惯性矩I 表示为截面积A 的函数:

根据《结构稳定理论》,轴心受压杆件的欧拉临界力可由式Pcr计算。μ 为杆件有效长度系数,其值由轴心受压杆件的边界支承条件确定。而三角挂篮的立柱可视为两端铰接的轴心受压杆件,对应的μ 值为1.0,故立柱的欧拉临界力为
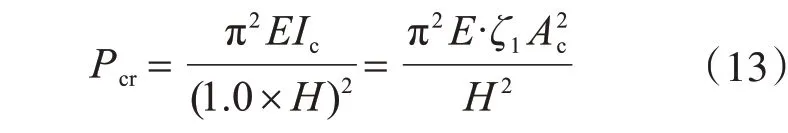
式中,Ic为立柱的截面惯性矩,其值由式(9)求得。
立柱最大应力值为
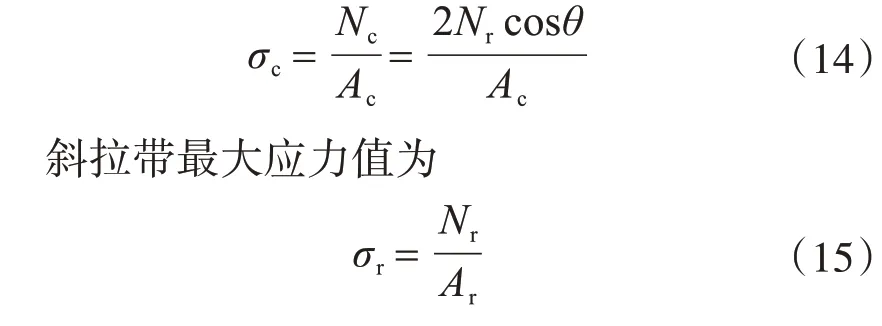
挂篮的整体形变值直接影响混凝土浇筑后箱梁高程位置,是控制悬臂施工质量的一项重要参数。挂篮的变形主要由吊带和主桁两部分的变形组成,吊带变形可以使用吊带轴力方便获得,主桁最大变形值可以将图2 中的F 替换为单位荷载并基于虚位移原理计算获得,最终将两部分变形叠加即可得到三角挂篮整体最大形变:
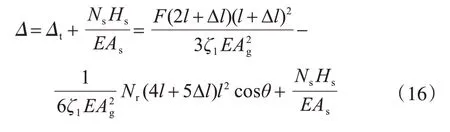
2 数学模型正确性验证
为检验挂篮设计参数优化数学模型的正确性,选用重庆高家花园大桥复线桥的平衡悬臂施工中的三角挂篮为对象。高家花园大桥复线桥为跨径(140+240+140)m 的三跨预应力连续刚构桥,主梁采用单箱双室截面,箱梁顶板宽25 m,底宽16 m,两侧翼缘板悬臂长4.5 m,悬臂板端部厚20 cm,根部厚70 cm,箱室内顶板厚0.32 m,底板厚度由箱梁根部的1.5 m变化至跨中0.32 m。
悬臂浇筑施工时单箱双室箱梁使用挂篮一次整体浇注成箱,由于截面宽度达到25 m,长度L为2.5 m 的1 号块重量达到484.6 t,传统挂篮难以满足施工要求,需要单独设计挂篮主桁结构。参考以往三角挂篮的相关参数,主桁架初步选择由3榀桁架组成,主桁高度取为4.4 m,长度Lg=12.2 m的主纵梁选用双拼I63b 工字钢(Ag=0.040 m2),立柱、斜拉带选用双拼C40a 槽钢(Ac=Ar=0.021 m2),前吊带采用8 根直径32 mm 的精轧螺纹钢作为中间吊带、120 mm×30 mm 的钢板作为两边吊带(前吊带总截面面积Ns=0.013 6 m2),主桁架与前吊带的总用钢量为22.15 t。三角挂篮的布置见图3。
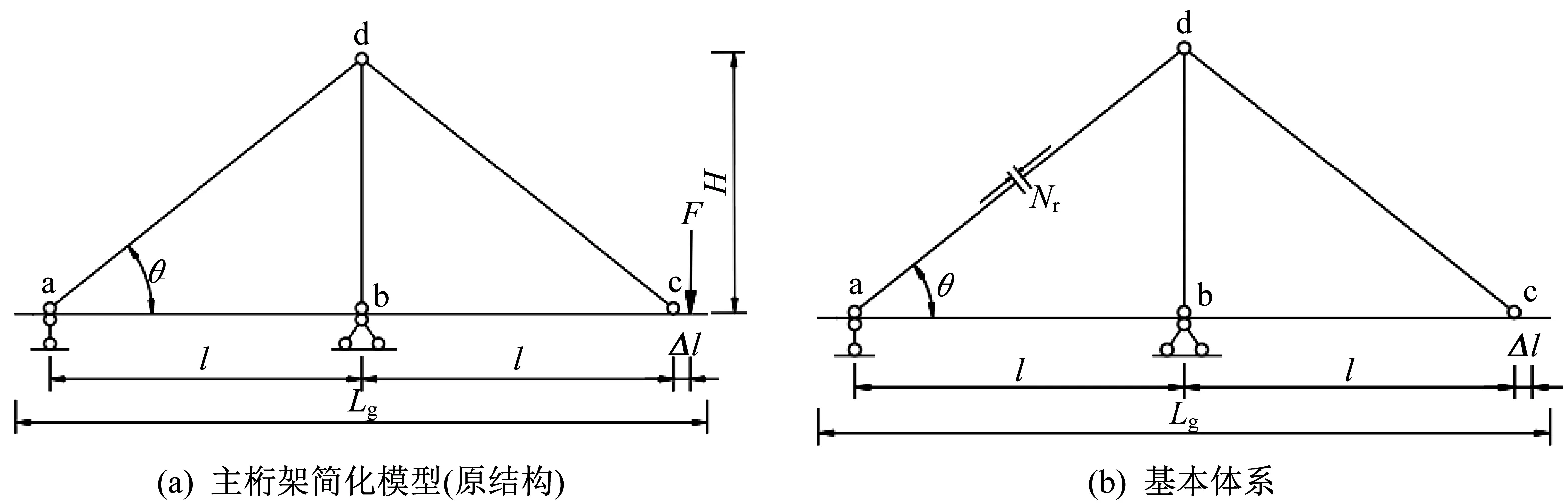
图2 主桁架简化模型和基本体系Fig.2 Simplified model and basic system of primary truss
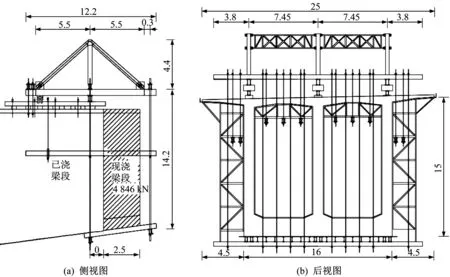
图3 三角挂篮总体布置图(单位:m)Fig.3 Overall layout of triangle form traveler(Unit:m)
依照上述参数使用Midas/civil 建立如图4 所示的有限元模型,主桁架纵梁、立柱、斜拉带、吊带、下滑梁、纵梁和下横梁均使用梁单元模拟,但立柱、斜拉带、吊带需要释放梁端转动约束,基于条分法将梁段自重等效为梁单元均布荷载并施加于滑梁和下纵梁上,上横梁与主纵梁之间设置为弹性连接的刚性连接约束,挂篮后锚点和下锚点设置为固定约束。
使用式(11)-式(16)计算挂篮主纵梁、立柱、斜拉带应力、立柱欧拉临界力和挂篮总体变形,计算结果如表1 所示,作为对比,表1 还给出了Midas/Civil 有限元计算结果,结果显示立柱的轴力不到欧拉临界力的3%,受压构件不会有失稳的风险;总体而言,数学优化模型的计算值与有限元计算结果吻合良好但并不完全一致,造成两种模型计算结果差异的原因可能是由于数学模型没有考虑挂篮主桁架自重。实际工程中三角挂篮主桁工作应力一般较小,挂篮整体变形和倾覆稳定是挂篮结构的控制荷载工况,基于数学简化模型得到的挂篮整体变形值更大、更保守,因此使用数学简化模型对挂篮设计参数进行优化分析是合适的。
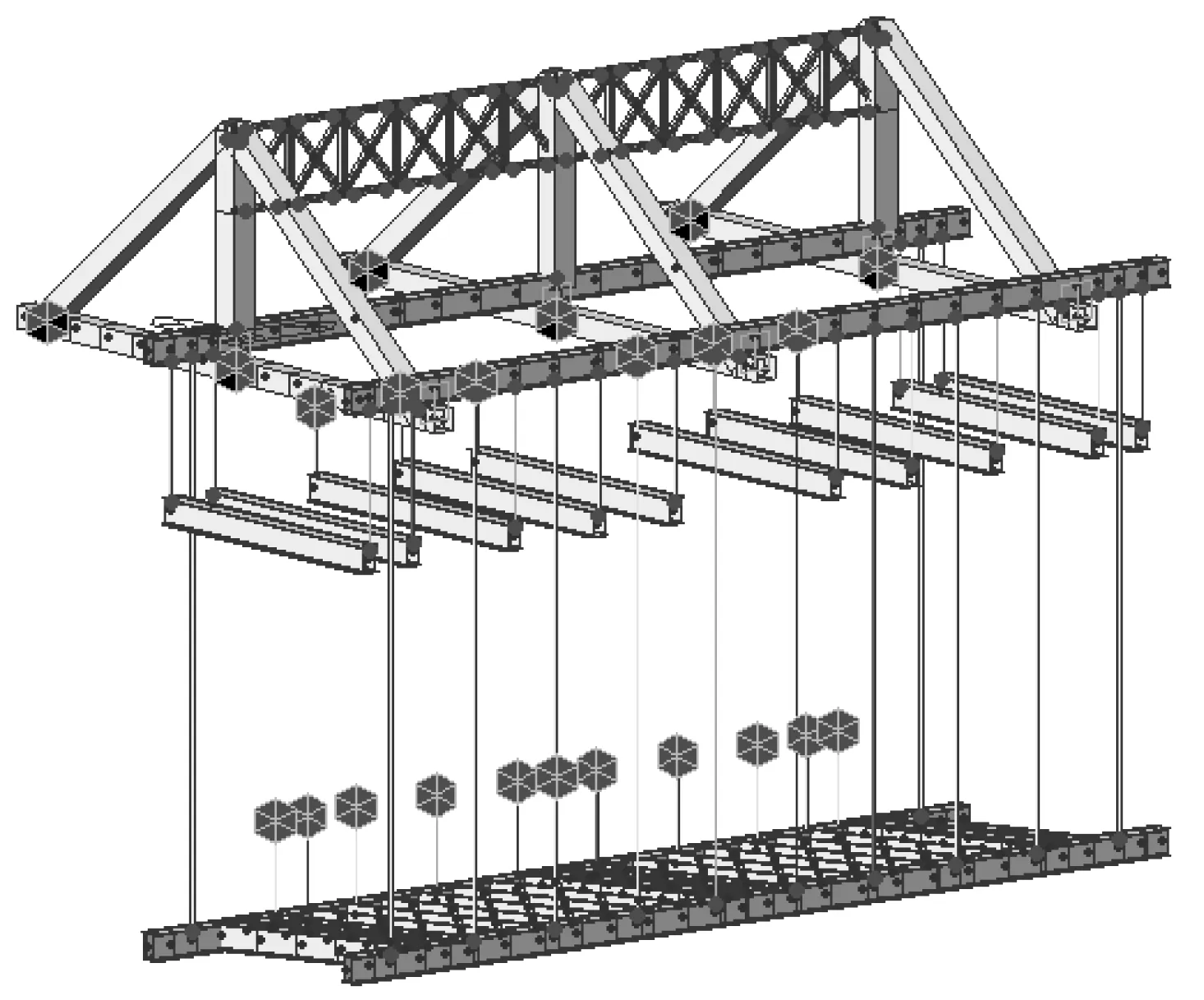
图4 三角挂篮midas模型Fig.4 Midas model of triangular form traveler

表1 不同方式计算结果对比Table 1 The comparison of results in different computing ways
3 挂篮设计参数的优化求解
以高家花园复线桥悬臂浇筑施工中使用的三角挂篮为优化对象,使用遗传算法实现挂篮设计参数的优化求解。遗传算法需要首先生成种群,本例设置种群数为300,遗传算法主要有“选择”“交叉”“变异”3 种基本操作[13],“选择”是通过定义“适应度函数”(适应度值越小越好)来筛选种群中优良的个体,使它们有机会作为父代为下一代繁衍子孙,本文优化目的要求用钢量越少越好,故将目标函数用钢量Sc设置为适应度函数,设置应力σmax≤190 MPa、σs≤415 MPa、整体最大形变值Δ≤20 mm、0.025 m2≤AS≤0.019 6 m2为非线性约束条件;“交叉”可以使种群得到新一代的个体,对每一个个体以交叉概率(crossover rate)来交换它们之间的部分染色体,体现着信息的交换[14],本例设置交叉概率为0.92;“变异”则在种群中随机筛选一个个体,并以“变异概率”(mutation rate)使个体变异为新的个体,使遗传算法更具有有效性[15],本例设置变异概率为0.05。经过600 代的迭代后,挂篮用钢量趋于稳定的14.62 t(图5),相比于初步设计的22.15 t,用钢量减少了34%。
600 次迭代后遗传算法给出的挂篮优化设计参数为H=4.73 m、Ag=0.015 7 m2、Ac=0.021 2 m2、Ar=0.016 3 m2、As=0.019 6 m2,依据此理论优化参数,主纵梁选用400 m×400 mm×11 mm 方钢管(Ag=0.017 1 m2),立柱选用400 mm×400 mm×14 mm 方钢管(Ac=0.021 6 m2)、斜拉带选用400 m×400 mm×11 mm方钢管(Ar=0.017 1 m2),吊带选用10根直径50 mm的精轧螺纹钢(总截面面积Ns为0.019 6 m2),此时主桁架和前吊带的用钢量共15.0 t。为更好地对比设计参数优化前后挂篮各构件的内力效应,表2 给出了使用遗传算法优化前、后挂篮各构件的应力、立柱欧拉临界力和整体变形。从中不难发现:参数优化后挂篮总用钢量减少32%,前吊带和主纵梁应力虽有明显增大,但均能满足规范要求,挂篮整体变形、立柱和斜拉带应力增幅并不明显;立柱轴力依然不到欧拉临界力的3%,结构优化不会带来受压构件失稳的不良影响;立柱和斜拉带的材料强度利用率仅有30%左右,但挂篮整体变形已接近规范容许限值,可见三角挂篮变形是控制设计的主要技术指标。
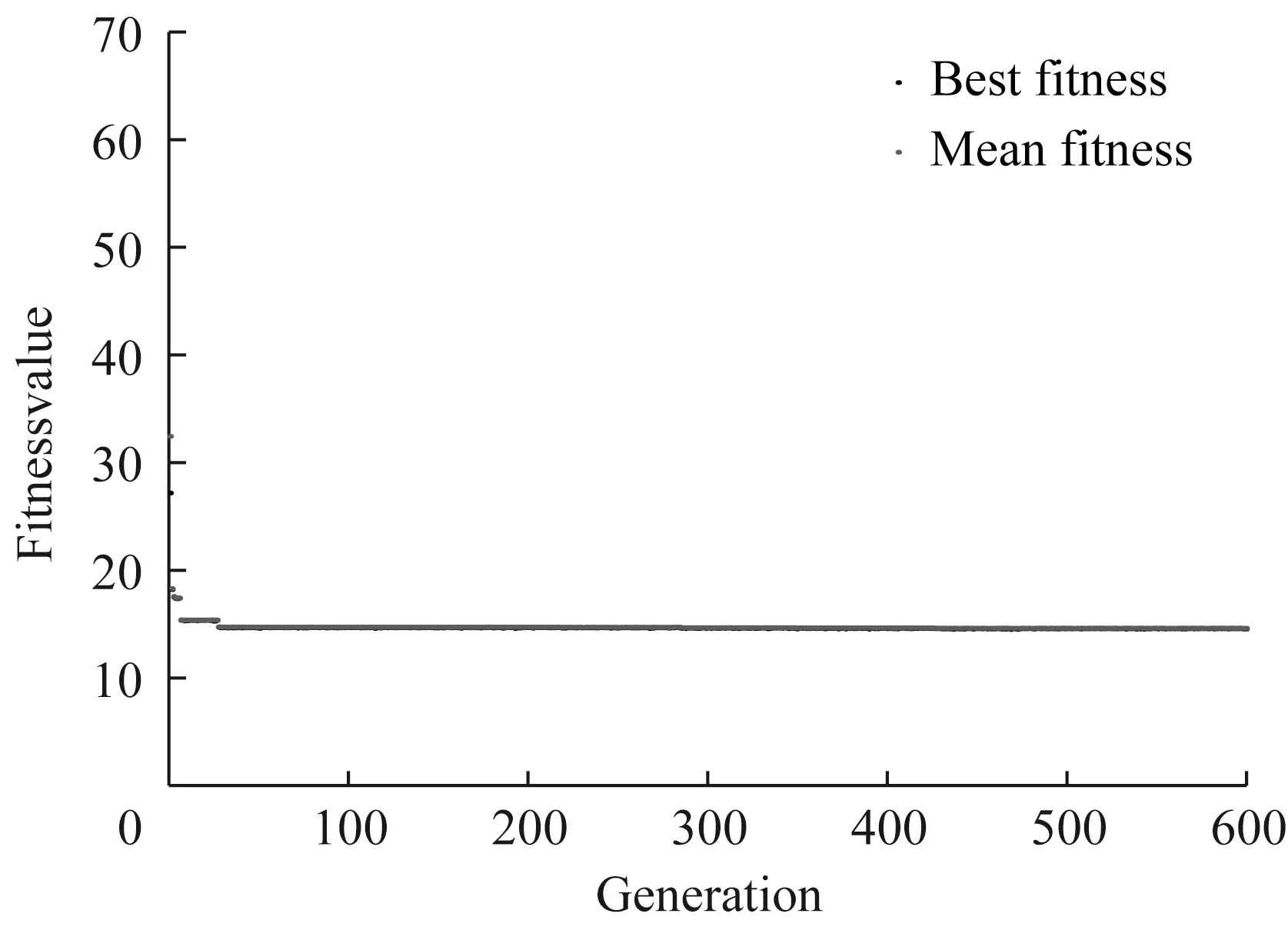
图5 迭代次数-目标函数值图Fig 5 Diagram of Generation-Fitness falue

表2 优化前后计算结果Table 2 Computing results before and after optimization
遗传算法给出的最优前吊带面积已接近优化模型的最大限值,前吊带面积的进一步增加有可能还会降低挂篮整体变形或者用钢量,为此通过调整前吊带总面积As的最大限值,并使用遗传算法重新分析不同限值条件下挂篮用钢量及其最优设计参数。
为说明前吊带面积的最大限值对挂篮力学性能和经济性能的影响,图6(a)指出,在一定程度下,最优解As的取值与As限值同步增长并且最大形变值都处于逼近限值的状态;图6(b)给出了不同限值条件下挂篮各构件强度利用率和用钢量,从中可以看出:随着前吊带总截面积的增大,挂篮各构件强度利用率将有所提高,而总体用钢量则随之减小,这表明使用总截面面积大的前吊带经济性更高,但由于受到单根精轧螺纹钢截面积的限制,要增大As就需要设计更多数目的吊带,这无疑会大大增加施工的繁琐性和难度。故建议前吊带的边吊带采用钢板制作的钢吊带来增大前吊带的总截面面积以达到节省用钢量和发挥主桁架材料性能的目的。
4 结 论
(1)使用本文数学优化模型可以方便、准确、高效地求解挂篮结构的力学效应,也可以利用本文公式实现挂篮力学效应的快速计算,或在满足规范要求的前提下完成挂篮构件截面尺寸的初步拟定。
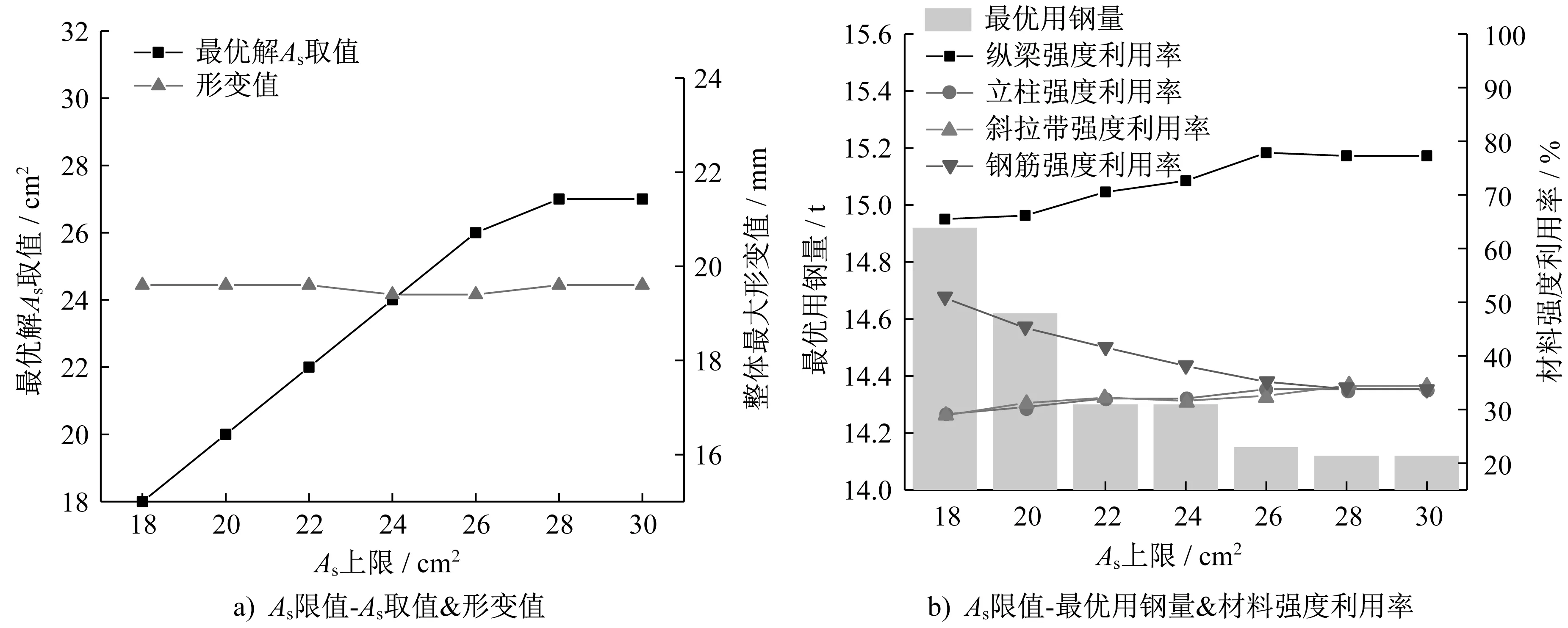
图6 As限值-主桁架受力性能图Fig.6 Diagrams of As limiting value-mechanical behavior of primary truss
(2)挂篮整体变形是控制挂篮设计的最主要因素,且前吊带刚度对挂篮整体变形影响显著,在不增加施工难度的前提下使用钢板或开孔钢板制作前吊带,可以减少主桁架的用钢量并最大限度地降低挂篮整体变形。
(3)三角挂篮优化前后受压构件的轴力皆不足其欧拉临界力的3%,构件不会失稳;三角挂篮的设计验算中,挂篮的整体稳定性是需要考虑的重要因素,本文对这一方面的研究还有所欠缺,需要更进一步地研究。
