某减震结构的优化设计
2020-11-12黄慧隆郭远翔
黄慧隆 郭远翔
(1.华南理工大学建筑设计研究院有限公司,广州510640;2.华南理工大学土木与交通学院,广州 510640)
0 引 言
消能减震指在房屋结构中设置消能器,通过消能器的相对变形和相对速度提供附加阻尼,以消耗输入结构的地震能量,达到预期防震减震的要求[1]。由于该方法减震效果明显,减震机理明确,因此近年来发展迅速[2],其优越的抗震性能已经在很多工程实例中得到证实[3]。如今阻尼器技术已经广泛应用于工业建筑和大型公共建筑中[4]。由于实际工程设计中采用消能减震技术的建筑结构需进行大震动力弹塑性分析,考虑到设计时间以及部分设计人员对大震动力弹塑性分析不熟悉等因素,目前常见的设计方法一般是由消能减震产品生产厂家配合结构工程师完成设计。对于一些项目,支撑的布置位置、数量及屈服力均由厂家提供给结构工程师,不少厂家对于减震产品的性能特点非常熟悉,但对于结构的整体设计概念的理解往往不够透彻,而部分结构工程师由于缺乏对消能减震支撑设计的深入理解以及没有时间对大震弹塑性分析结果进行反复分析及调试,往往无法准确判断厂家提供的方案是否合理及能否进行优化。
本文结合一个实际工程例子,对比分析了三种不同的带复合金属阻尼器支撑的减震设计方案,旨在为相关实际工程提供参考。
1 工程概况
本项目位于北京市,建筑共六层,其中第六层为局部小屋面,为多层建筑结构,结构模型如图1所示。抗震设防烈度为8 度,设计分组为第二组,Ⅲ类场地,设计基本地震加速度为0.2 g,基本风压为0.45 kN/m2,地面粗糙程度为B类。原建筑主体采用框架-剪力墙结构,改造后保留的部分为框架结构,因此需对保留部分结构进行减震加固设计。本工程采用带复合金属阻尼器支撑进行减震设计,支撑类型均为人字形支撑。支撑均选择布置在建筑的最外侧,一方面考虑到对建筑使用功能的影响较小,另一方面可使得结构增加侧向刚度的同时保证足够的抗扭刚度。
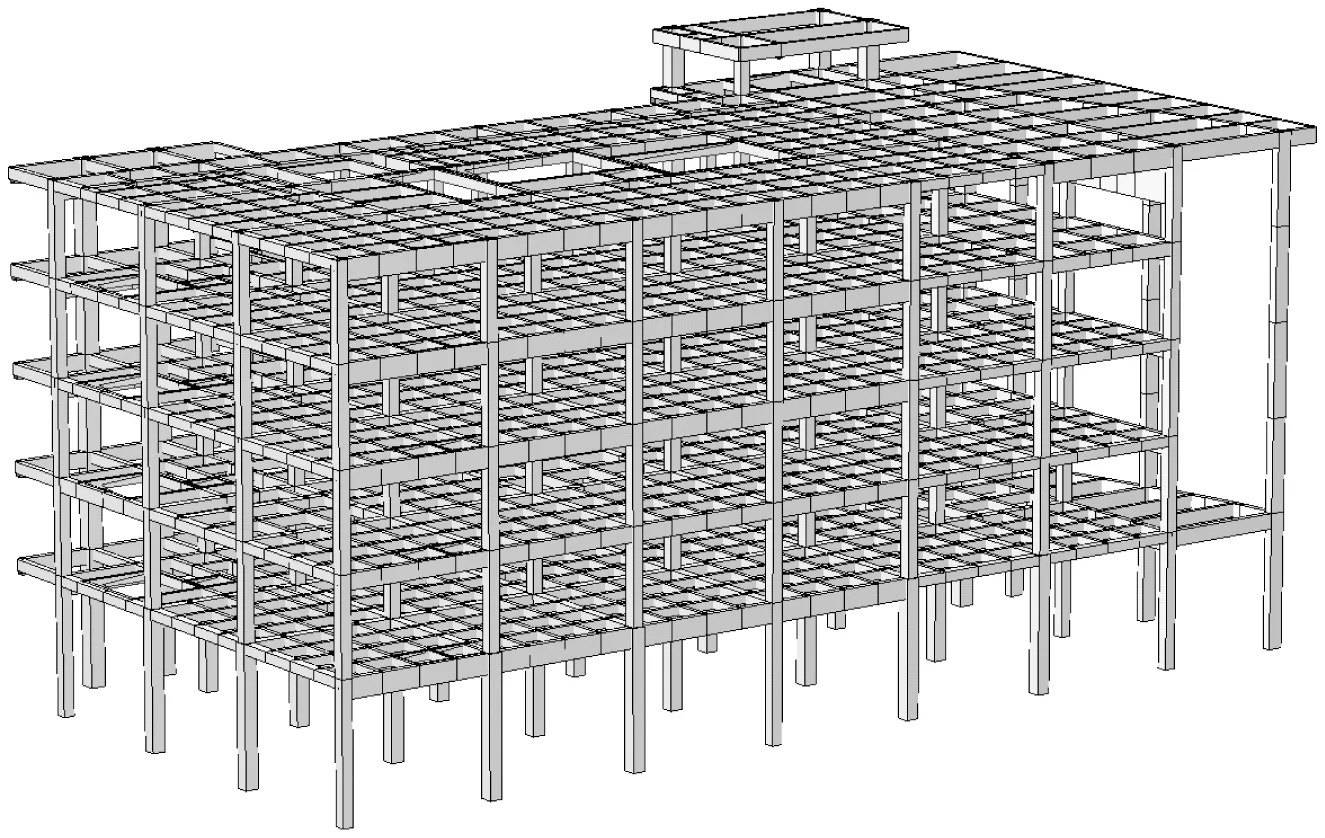
图1 结构模型图Fig.1 The structure model
本文对比分析了三种不同的设计方案,其中方案一为消能减震产品生产厂家提供,方案二及方案三为设计人员在厂家布置方案基础上作了调整后的情况。方案一的阻尼器支撑平面布置情况如图2 粗线框所示,布置数目如表1 所示;方案二及方案三的阻尼器支撑平面布置情况如图3 粗线框所示,布置数目如表2 所示。方案一及方案二中复合金属阻尼器屈服力均为1 500 kN,方案二与方案三中的复合金属阻尼器布置位置及数目均相同,但部分复合金属阻尼器的屈服力不同,其中方案三在粗虚线方框处的复合金属阻尼器屈服力为1 000 kN,其余为1 500 kN。
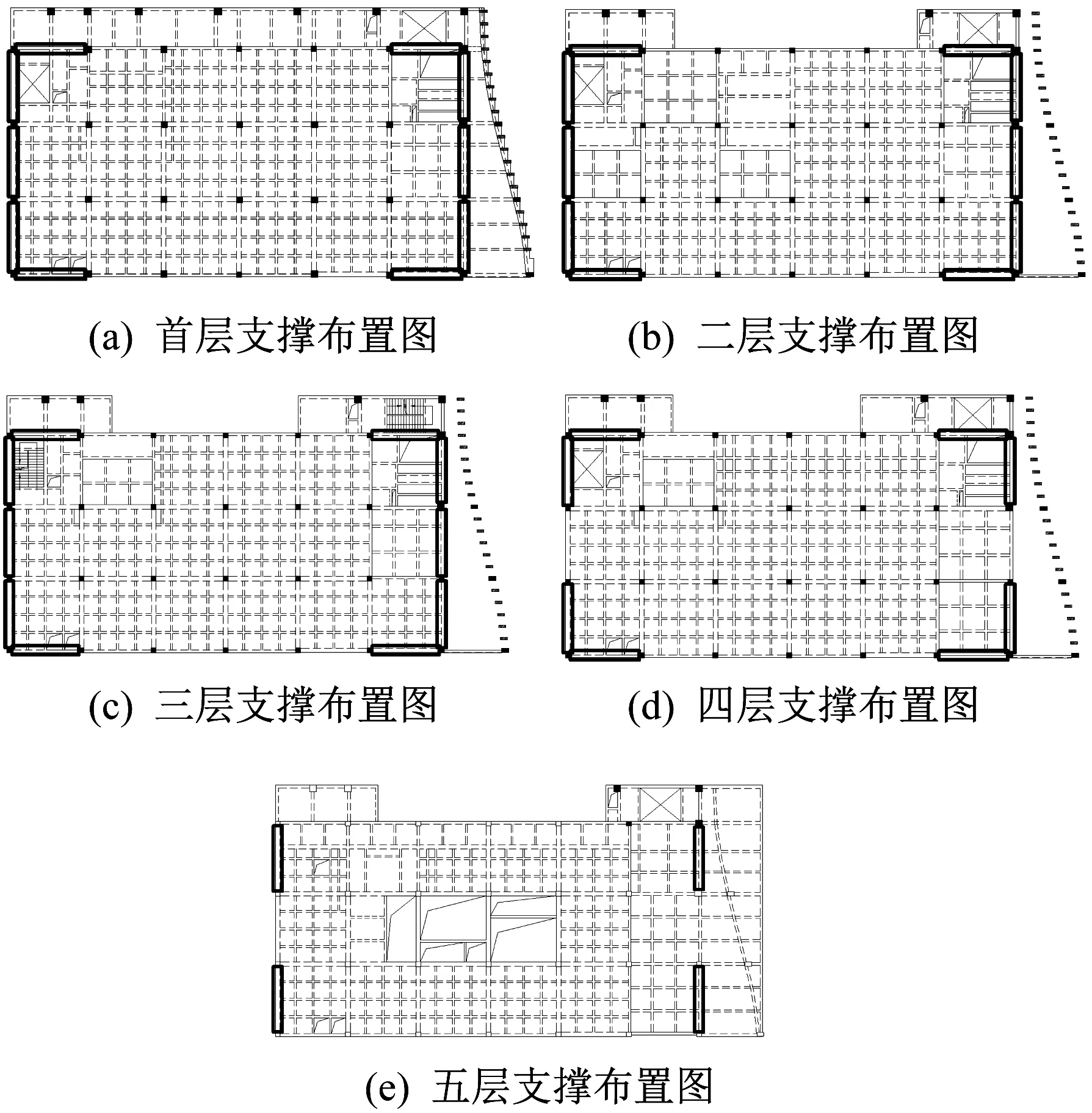
图2 方案一支撑布置平面图Fig.2 The brace layout plan of the first scheme
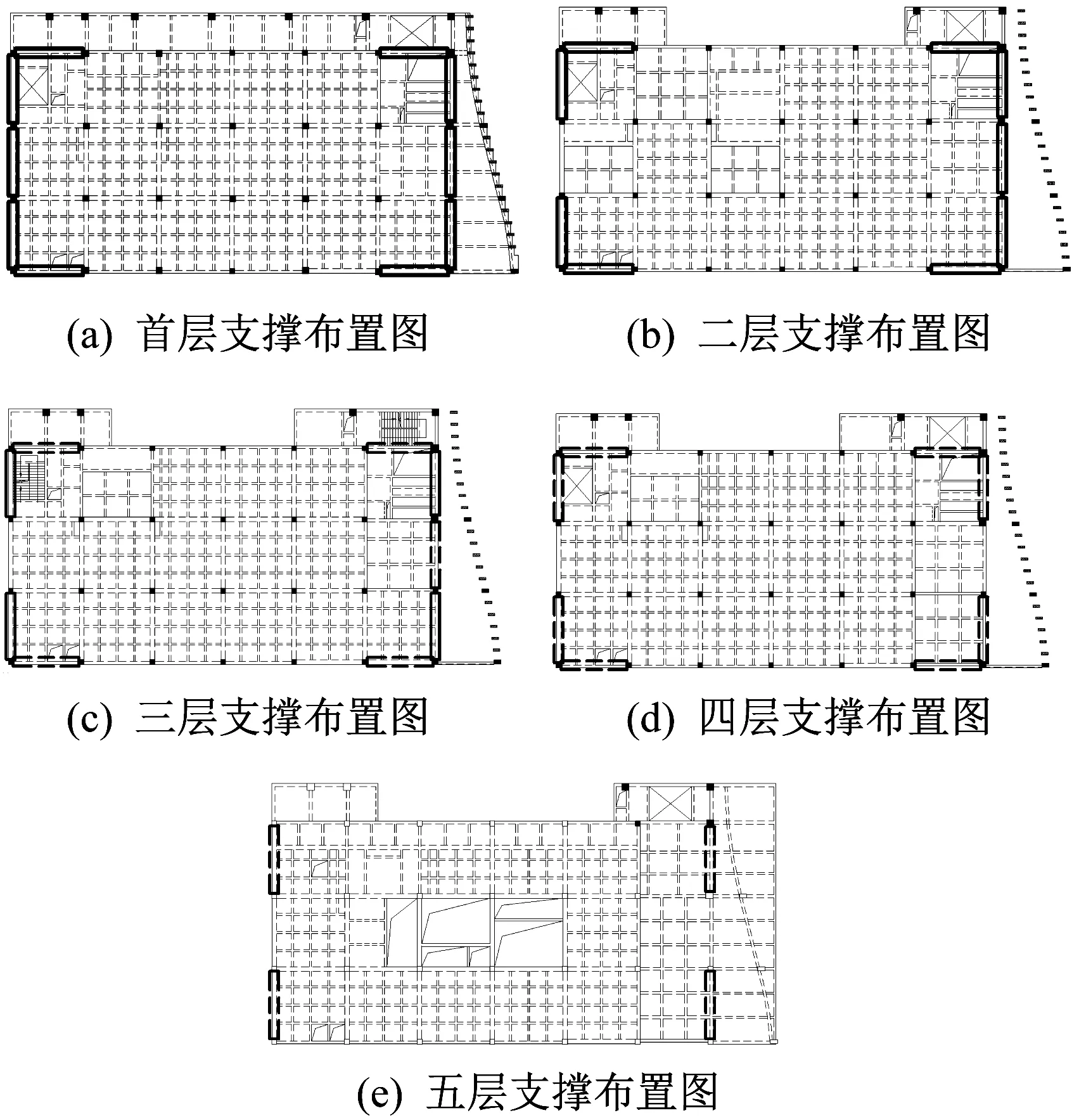
图3 方案二及方案三支撑布置平面图Fig.3 The brace layout plan of the second and the third scheme
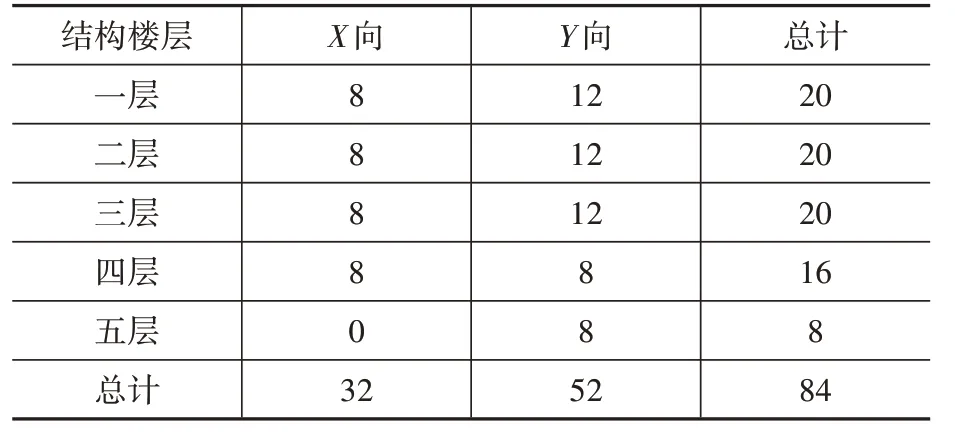
表1 方案一支撑布置数量Table 1 The number of brace of the first scheme 个
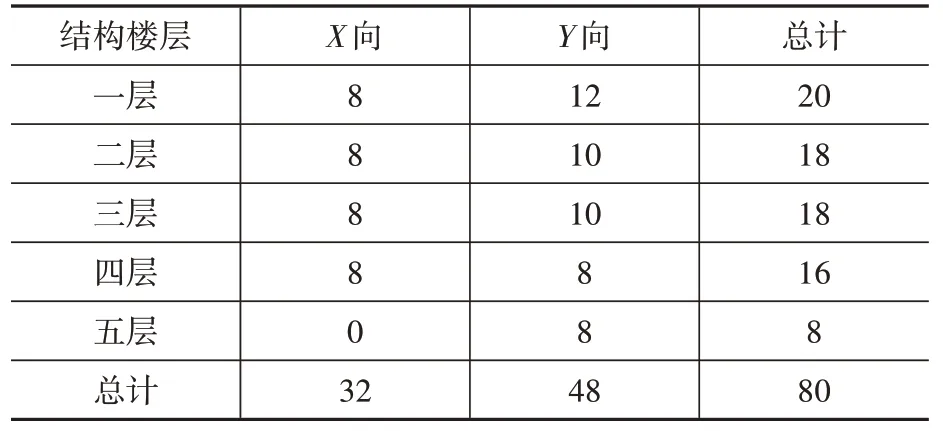
表2 方案二及方案三支撑布置数量Table 2 The number of brace of the second and the third scheme 个
2 计算模型的建立
本工程小震情况下的反应谱计算采用有限元软件YJK,小震情况下的动力弹性时程分析采用有限元软件Sap2000,大震情况下的动力弹塑性时程分析则采用有限元软件Perform-3D。根据《建筑抗震设计规范》(GB 50011—2010)[1]的要求,弹性时程分析时,每条时程曲线计算所得的结构底部剪力不应小于振型分解反应谱法计算结果的65%,多条时程曲线计算所得结构底部剪力的平均值不应小于振型分解反应谱法计算结果的80%。本工程设计选用Landers、Chi-Chi_Taiwan(042)(以CCT(042)简称)、Hector Mine(以HM 简称)、Chi-Chi_Taiwan(082)(以CCT(082)简称)、San Fernando(以SF简称)、RGM1(人工波)、RGM2(人工波)七条地震波。经计算,所选时程波均能满足规范规定。
3 多遇地震作用下结构反应谱分析
目前对结构进行消能减震设计时,对于多遇地震的反应谱计算主要是以YJK 或者PKPM 等软件为主。本文对三个方案采用YJK进行小震的反应谱计算,并提取了位移角、基底剪力及倾覆弯矩进行对比,结果如表3和表4所示。
由表3 可以看到,三个方案的位移角均能满足规范1/550的限值要求,方案一与方案二在X向的位移角值几乎一样,而Y 向上由于方案二取消了二层与三层左侧在Y 向布置的两处阻尼器支撑,因此最大位移角楼层转移到二层。方案三由于三至五层的部分阻尼器支撑屈服力由1 500 kN减小至1 000 kN,导致阻尼器支撑的刚度也相应下降,因此X 向和Y 向最大位移角楼层分别转移到了第三层及第四层。
另外,方案二的Y 向首层位移角为1/672,方案三则为1/685,均小于方案一的1/607,而方案三的X向首层位移角也小于前两个方案。可见对于位移角来说,阻尼器支撑数目的增加及其屈服力的提高并不总是有利的。
由表4可以看到,方案一与方案二在X 向及Y向上的基底剪力及倾覆弯矩均相差不大,而方案三由于阻尼器支撑数目的减少且三至五层部分阻尼器支撑屈服力由1 500 kN 减小至1 000 kN,阻尼器支撑相应的等效截面面积及刚度也会减小,从而导致结构整体刚度下降,因此基底剪力与倾覆弯矩均小于前两个方案。
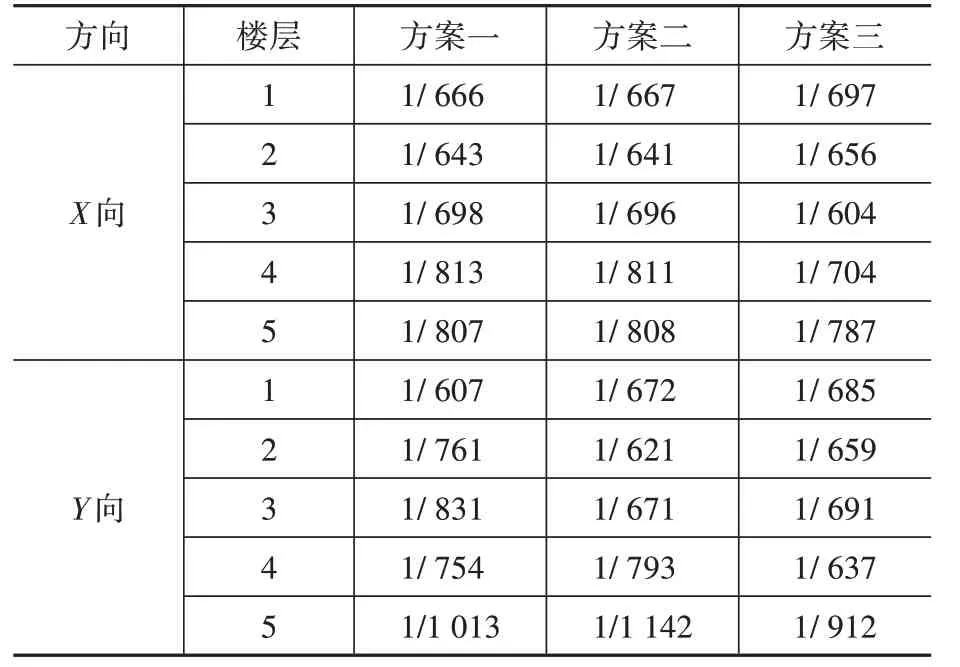
表3 各方案楼层位移角Table 3 The displacement angle of each scheme
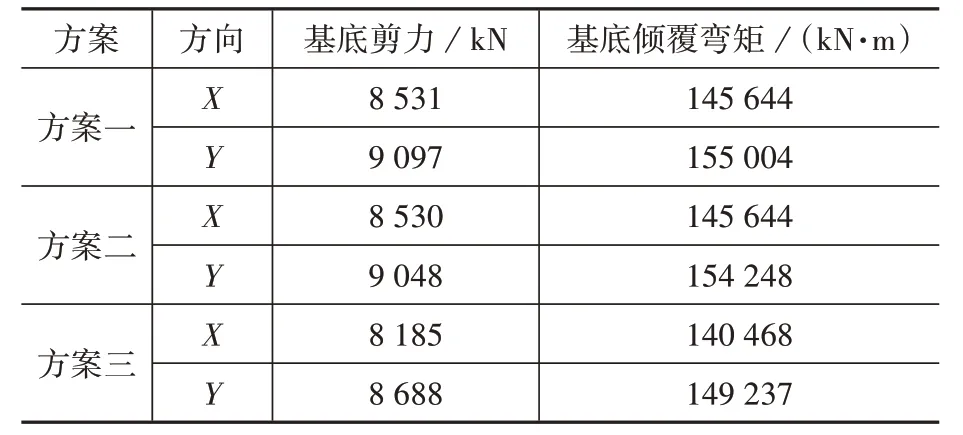
表4 各方案基底剪力及倾覆弯矩Table 4 The base shear and overturning moment of each scheme
4 多遇地震作用下结构动力弹性时程分析
本文采用Sap2000 对结构进行多遇地震下的动力弹性时程分析,考虑带阻尼器支撑的非线性,在Sap2000 中采用Wen 单元对带阻尼器支撑进行模拟。
对分析结果进行提取,表5和表6为各时程波作用下结构的X向和Y向楼层位移角,表7则为结构第五层右下角一点(图4 圆圈处,该点为采用YJK 进行多遇地震下反应谱计算的结果中位移较大位置)在各时程波作用下的最大位移值,表8 则为各时程波作用下的总基底剪力及框架部分基底剪力,其中总基底剪力由框架部分基底剪力与支撑承担基底剪力组成。
由表5和表6可以看到,在多遇地震下对结构进行动力弹性时程分析,三个方案的位移角均能满足规范1/550 的限值要求。由各方案的时程波分析结果的平均值可以看到,X 向上方案一与方案二的各层位移角相差很小,而方案三在一、二层的位移角小于方案一和方案二,其余各层相差不大。Y 向上方案二及方案三的一、二层位移角均小于方案一。
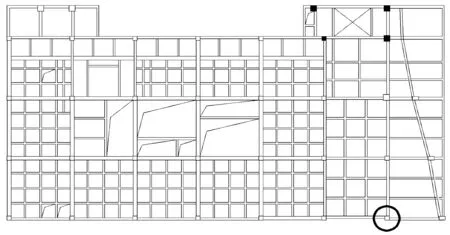
图4 时程分析下提取位移对应点Fig.4 The displacement extraction point of time history analysis
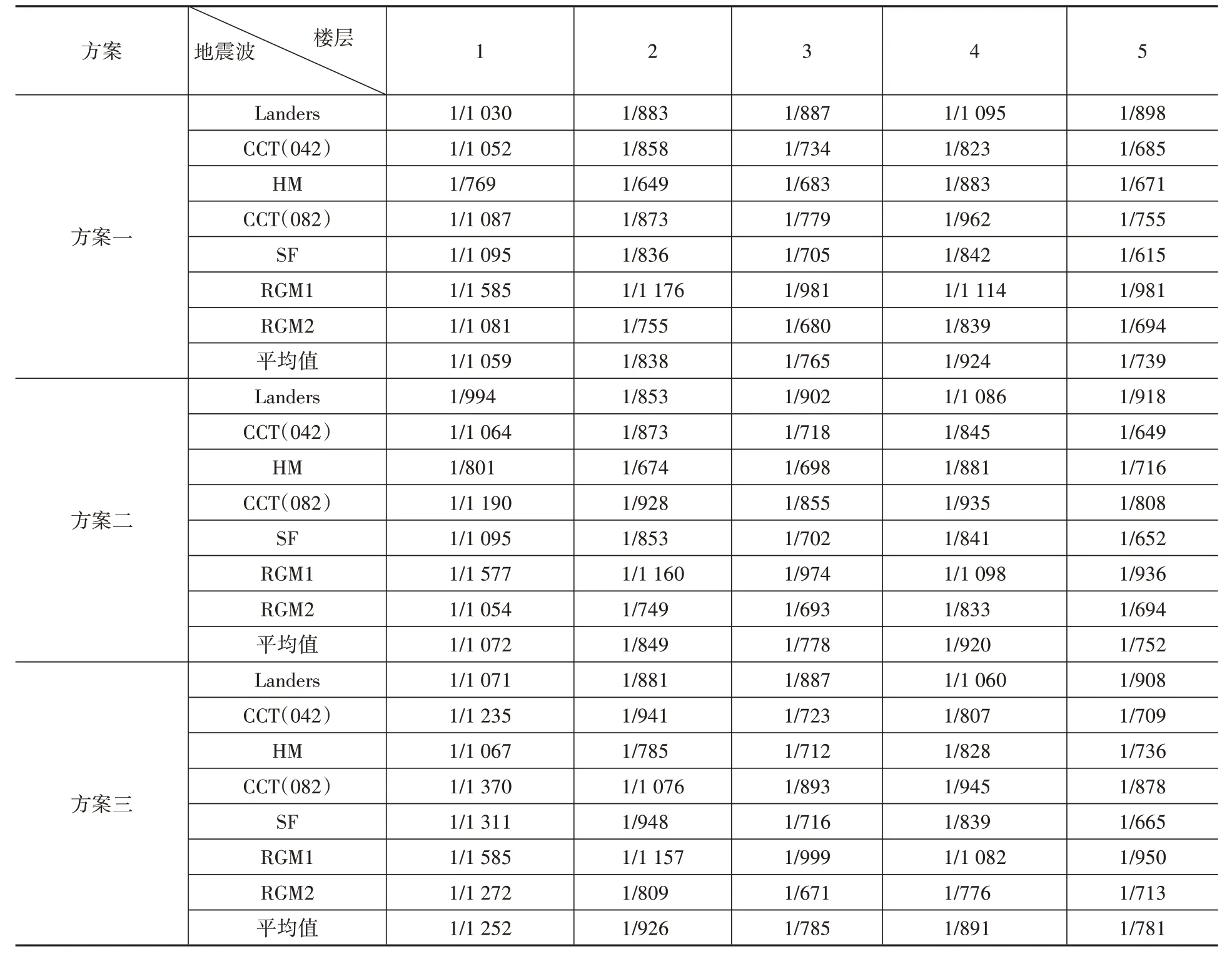
表5 小震动力弹性时程分析下结构层间位移角(X向)Table 5 The story drift of dynamic elastic time history analysis under small earthquake(X-direction)
由表7 中各方案的时程波分析结果的平均值可以看到,三个方案中结构在X 向的位移值均大于Y向位移值,另外各方案的位移值相差不大。
由表8 中各方案的时程波分析结果的平均值可以看到,X 向上方案三的总基底剪力值小于方案一与方案二的分析结果,Y 向上的总基底剪力值则在方案一与方案二之间。对于框架部分基底剪力,方案三在两个方向上均小于方案一与方案二的分析结果,这意味着框架部分结构在小震情况下受到的地震力更小。这对于需要进行加固改造的结构来说,显得尤为重要,一方面可以减少对结构构件加固而造成的损伤,另一方面也可以有效减少造价。
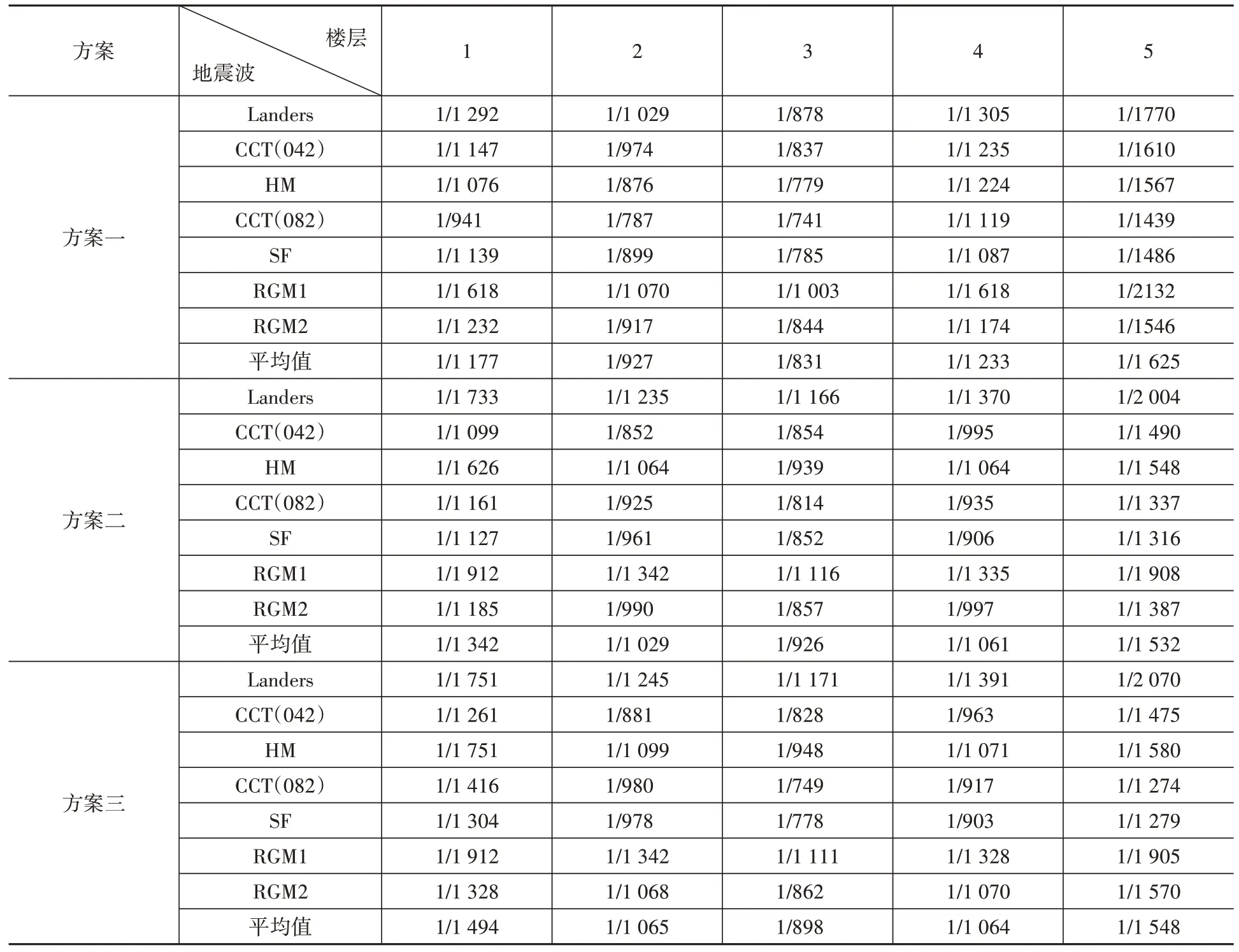
表6 小震动力弹性时程分析下结构层间位移角(Y向)Table 6 The story drift of dynamic elastic time history analysis under small earthquake(Y-direction)
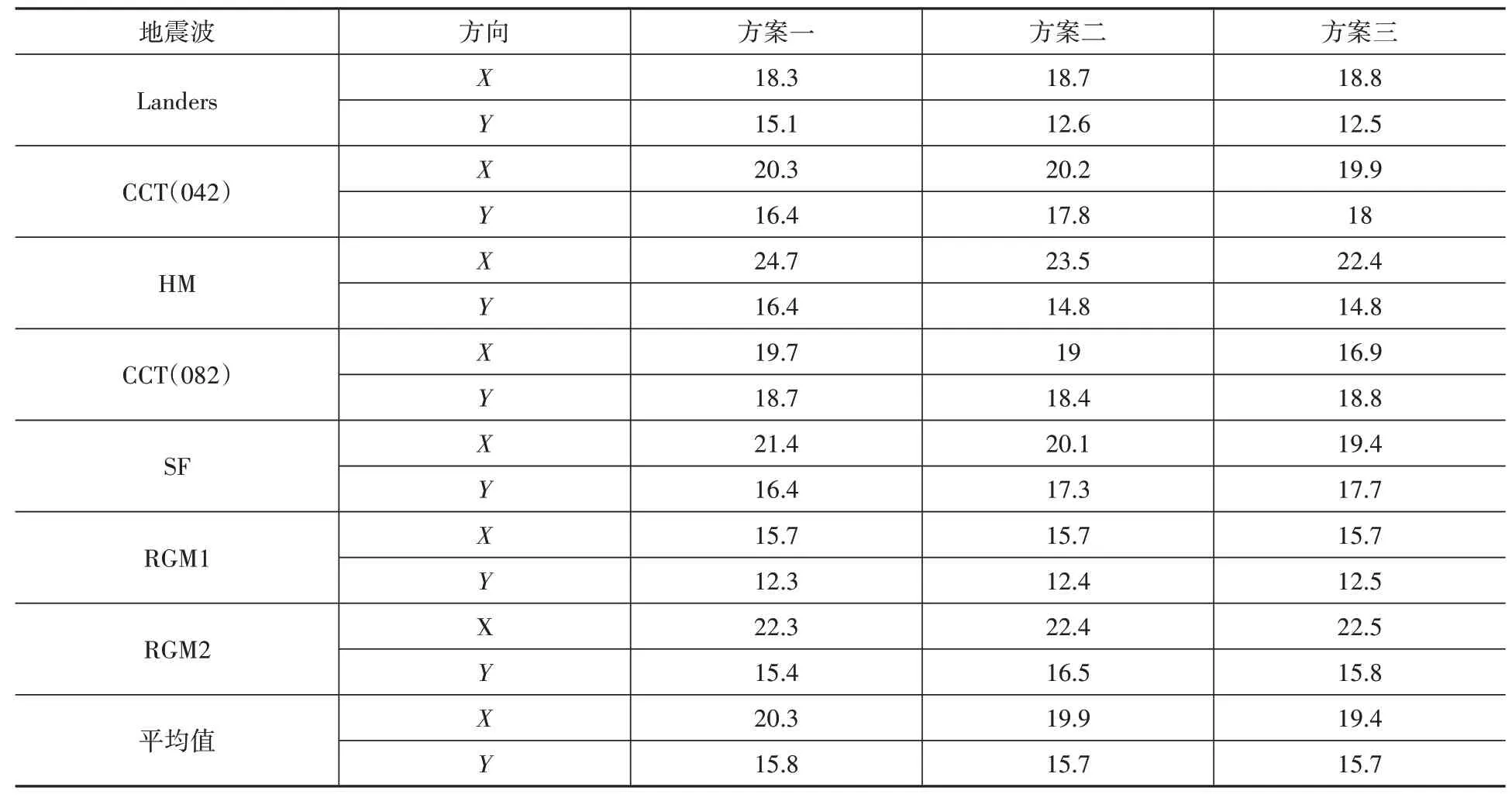
表7 小震动力弹性时程分析下提取点位移Table 7 The displacement of extraction point of dynamic elastic time history analysis under small earthquake mm
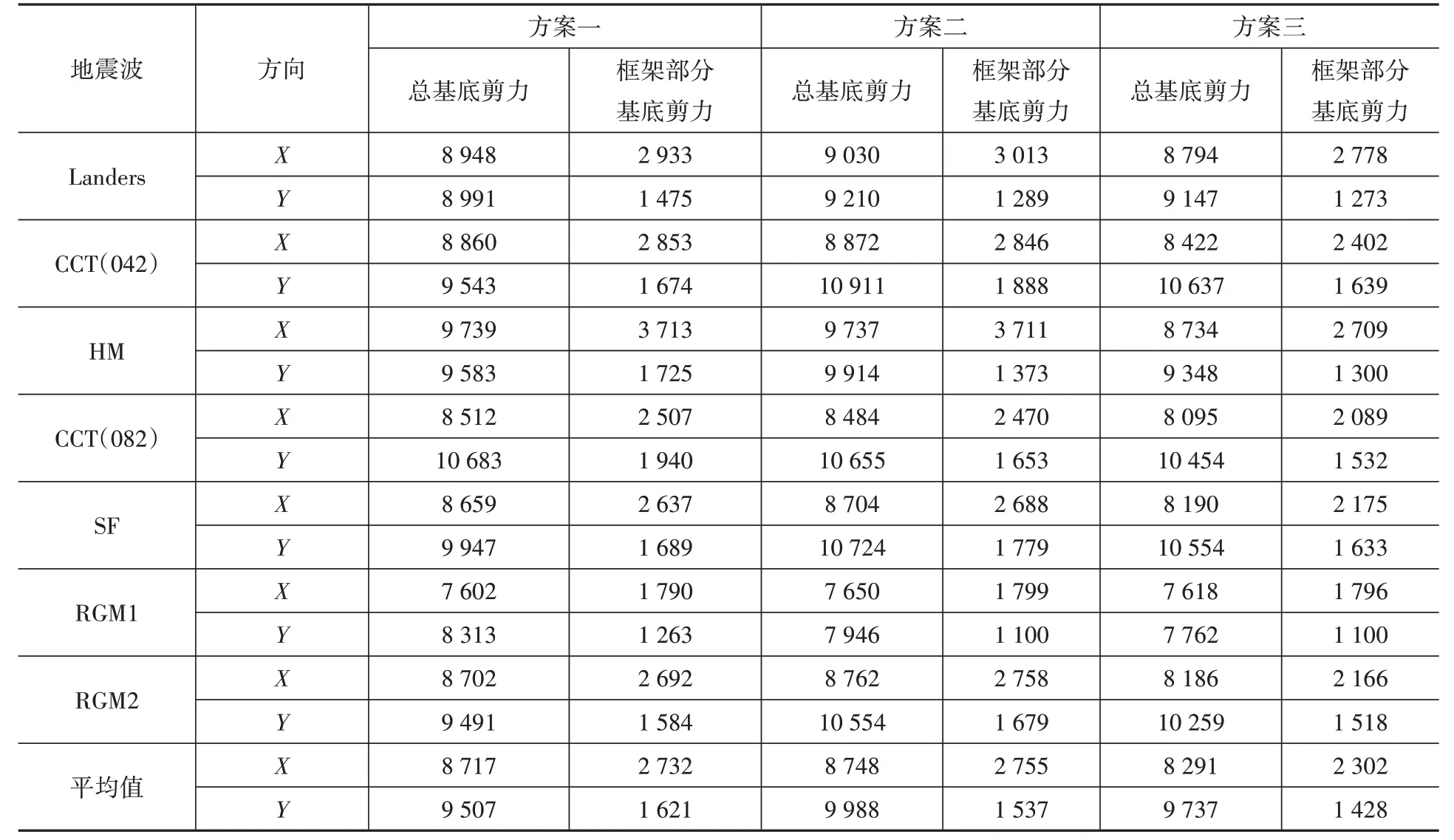
表8 小震动力弹性时程分析下结构总基底剪力及框架部分基底剪力Table 8 The base shear of the structurer and the frame part of the structurer of dynamic elastic time history analysis under small earthquake kN
由此可见,减少了支撑数量并降低了部分支撑屈服力的方案三在小震弹性时程分析后的位移角不但没有明显增大,一些楼层的计算结果反而小于方案一和方案二,且其框架部分基底剪力是三个方案中最小的。因此对于减震结构的设计,并不只是简单考虑增加阻尼器支撑数目,提高阻尼器支撑屈服力即可,支撑刚度的增加也可能会引起地震力的提高而导致楼层位移角变大,实际工程中宜根据结构楼层刚度分布情况,合理布置支撑,如在地震力较小的上部楼层可适当减小支撑数目或者降低支撑的屈服力。
5 罕遇地震作用下结构动力弹塑性时程分析
本文采用Perform-3D 对结构进行大震下的动力弹塑性时程分析。混凝土的压应力-应变关系采用Trilinear(三折线)模型,考虑强度损失和刚度退化效应,不考虑混凝土的受拉特性。钢筋的应力-应变关系采用三折线本构来模拟[5]。对梁柱单元均采用纤维模型,并考虑实配钢筋的影响,复合金属阻尼器则采用弹性支撑加BRB 单元来模拟[6]。
对分析结果进行提取,表9 和表10 为各时程波作用下结构的X 向和Y 向楼层位移角,表11 则为结构第五层右下角一点(图4 圆圈处)在各时程波作用下的最大位移值,表12 则为各时程波作用下的总基底剪力及框架部分基底剪力。
由表9 和表10 可以看到,在罕遇地震下对结构进行大震动力弹塑性时程分析,三个方案的位移角均能满足规范1/50 的限值要求。由三个方案的七条时程波平均值可以发现,X 向上方案一与方案二的各层位移角相差很小,这与小震下的反应谱及动力弹性时程分析结果一致。另外方案三在一层、二层和五层的位移角均小于方案一和方案二。Y 向上三个方案的首层位移角相差很小,方案一的二层、三层及四层的位移角小于其余两个方案,五层的位移角则是方案三的结果最小。
由表11 中各方案的时程波分析结果的平均值可以看到,三个方案中结构在X 向的位移值都大于Y 向位移值,方案二与方案三在两个方向上的位移值相差很小,且均小于方案一。
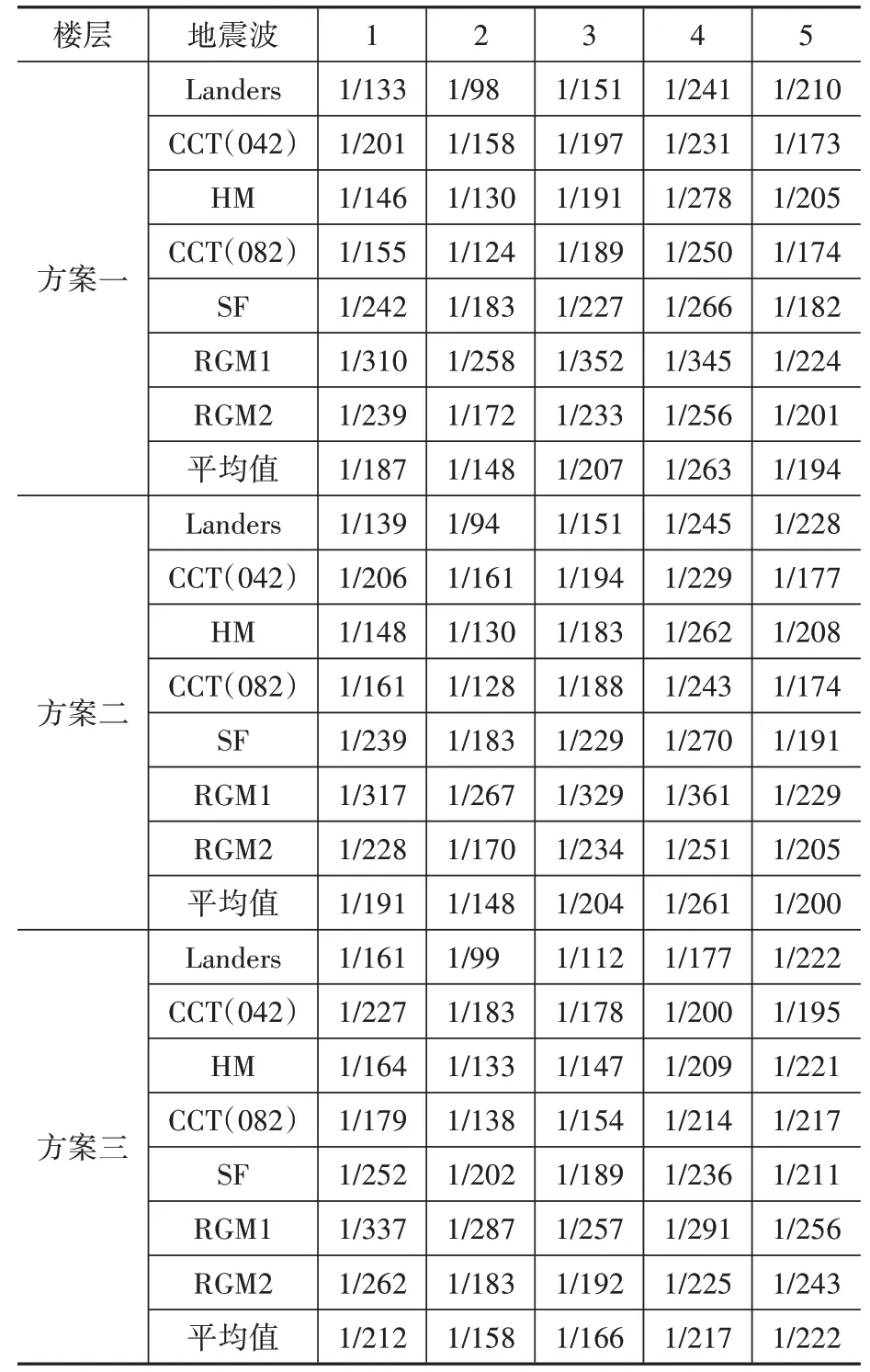
表9 大震动力弹塑性时程分析下结构层间位移角(X向)Table 9 The story drift of dynamic elastic-plastic time history analysis under major earthquake(X-direction)
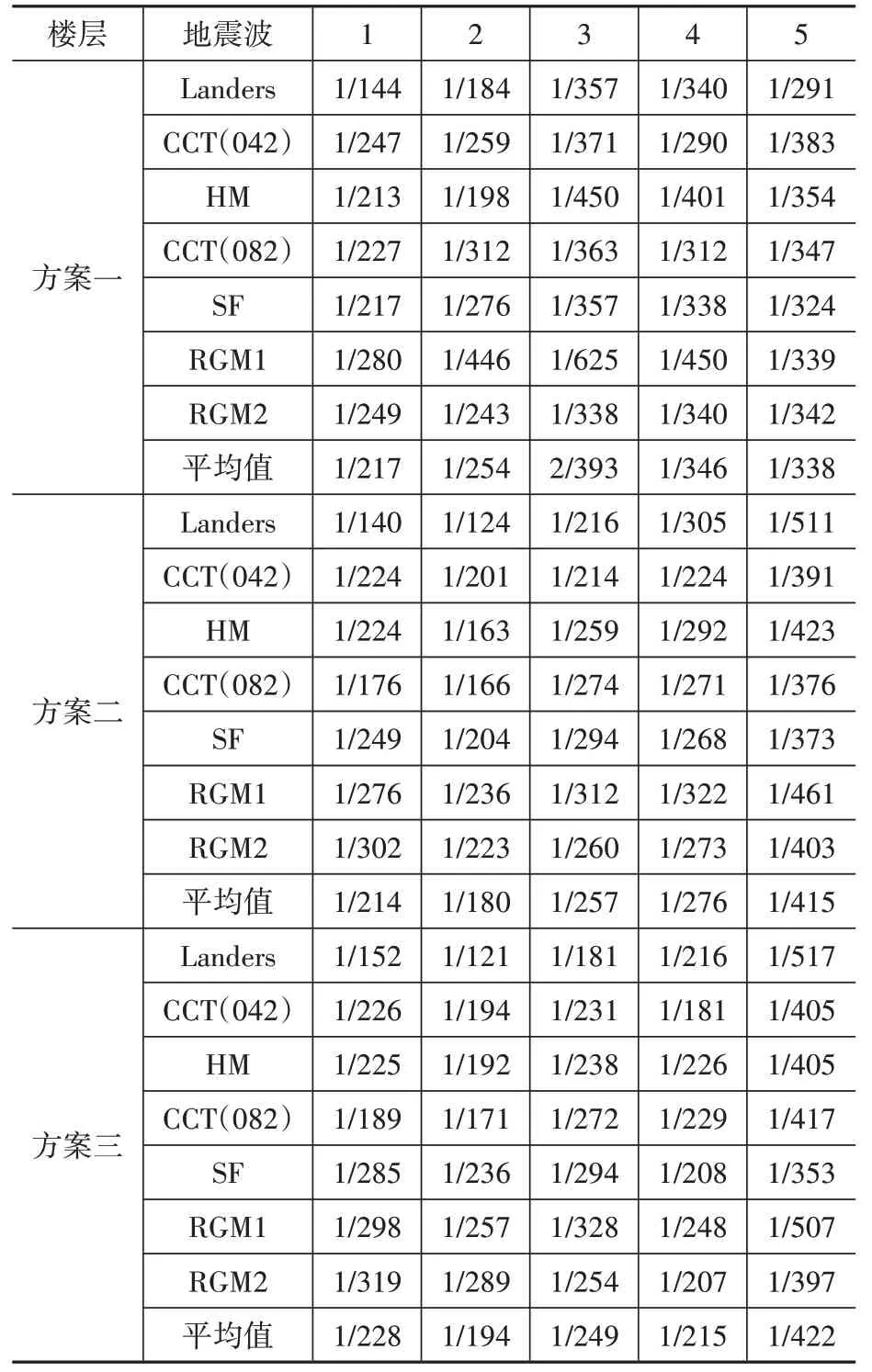
表10 大震动力弹塑性时程分析下结构层间位移角(Y向)Table 10 The story drift of dynamic elastic-plastic time history analysis under major earthquake(Y-direction)
由表12 中各方案的时程波分析结果的平均值可以看到,方案一与方案二在X 向上的总基底剪力及框架部分基底剪力几乎一样,Y 向上方案一则大于方案二;方案三在两个方向上总基底剪力及框架部分承担基底剪力均小于方案一与方案二,这意味着框架部分结构在大震情况下受到的地震力更小,框架部分结构受到的损伤也将更小,这也是减震结构设计的目的之一。
由此可见,减少了阻尼器支撑数量并降低了部分阻尼器支撑屈服力的方案三在大震动力弹塑性时程分析下的位移角不但没有明显增大,一些楼层的计算结果反而小于方案一和方案二,且其基底总剪力与框架部分基底剪力均是三个方案中最小的,故方案三不但在大震作用下框架部分的安全性更好,且在造价上也优于方案一与方案二。因此实际工程设计过程中,不应通过简单增加阻尼器支撑数目、提高阻尼器支撑屈服力来满足规范的位移角等限值要求。
图6 是三个方案在San Fernando 的Y 向时程波作用下提取的阻尼器支撑的滞回曲线,所提取的阻尼器支撑位于结构第四层中如图5 所示的半跨位置。由图6 可以看到,方案一与方案二的阻尼器支撑滞回曲线都不太饱满,方案二略优于方案一,而方案三的滞回曲线则显得非常饱满,因此在耗能能力上优于前两个方案,这是由于结构上部楼层层间地震力较小,此时较大的阻尼器屈服力不利于其耗能。方案三中上部楼层的阻尼器支撑在其余地震波作用下的滞回曲线同样较其余两个方案饱满,即耗能能力更优,这也是方案三在两个方向上总基底剪力及框架部分承担基底剪力均小于其余方案的重要原因之一。因此实际工程设计过程中,宜针对不同楼层选择阻尼器支撑的屈服力,如在上部楼层适当减小支撑的数量及屈服力,并结合大震动力弹塑性分析后的结果对阻尼器支撑的耗能情况进行优化。
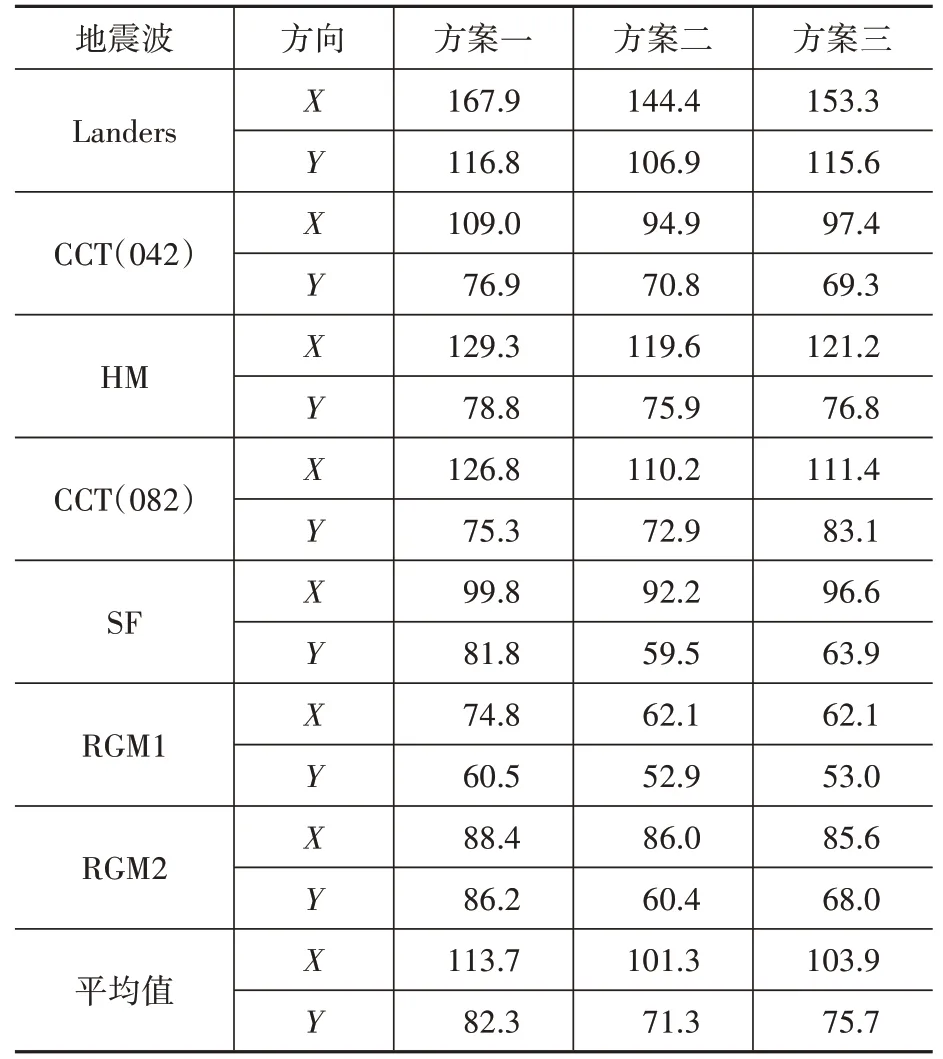
表11 大震动力弹塑性时程分析下提取点位移Table 11 The displacement of extraction point of dynamic elastic-plastic time history analysis under major earthquake mm
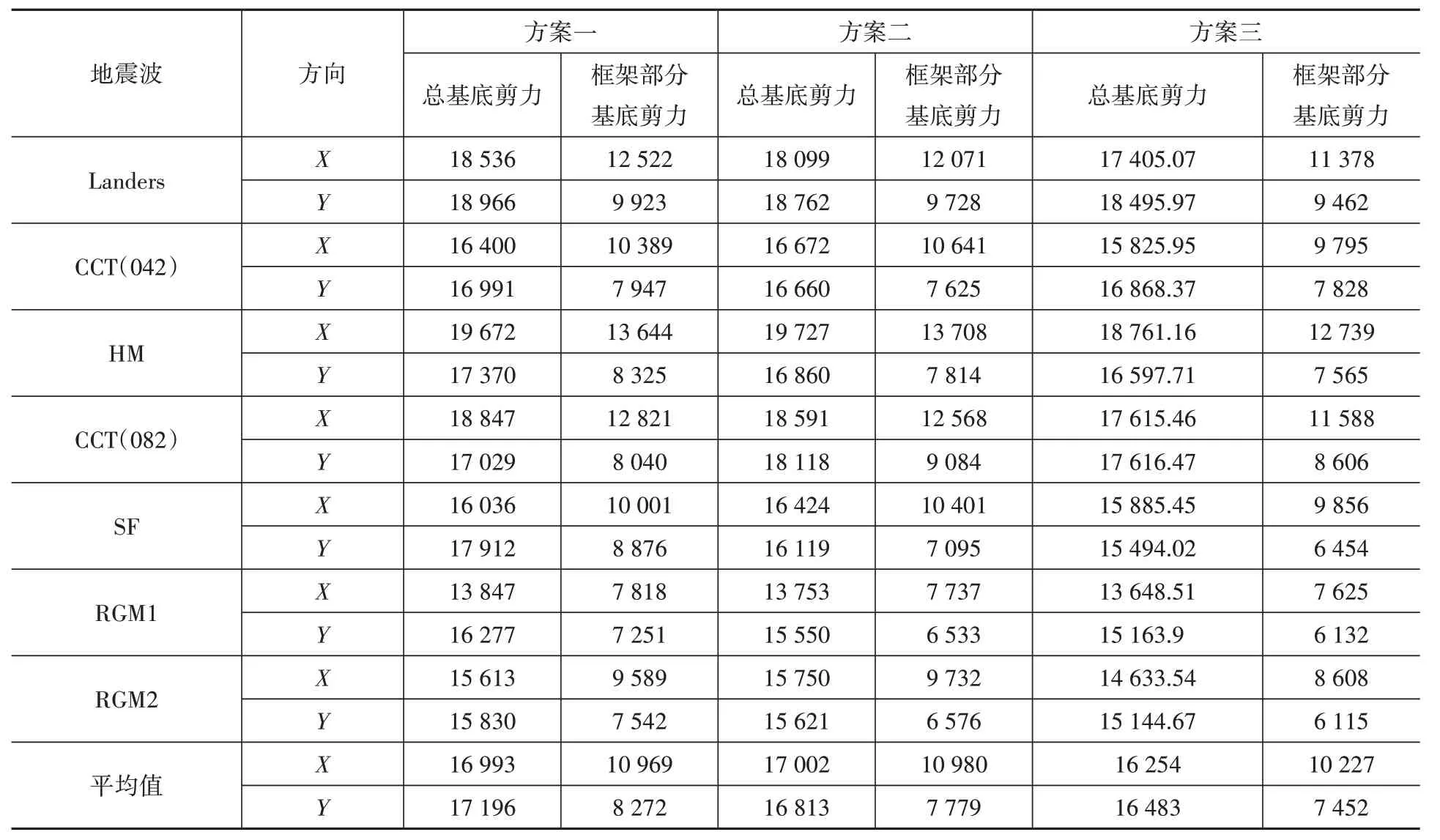
表12 大震动力弹塑性时程分析下结构总基底剪力及框架部分基底剪力Table 12 The base shear of the structurer and the frame part of the structurer of dynamic elastic-plastic time history analysis under major earthquake kN
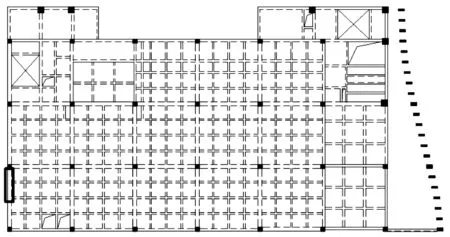
图5 提取滞回曲线的阻尼器支撑位置Fig.5 The position of brace that hysteretic curve was extracted
通过对该结构进行的小震反应谱分析、小震动力弹性时程分析及大震动力弹塑性时程分析可以看到,减震结构的优化设计对结构至关重要。三个方案在大震弹塑性分析下得出的结果中有部分规律与小震反应谱及小震动力弹性时程分析一致,因此实际的减震结构设计过程中,结构工程师应充分利用结构设计概念,在小震下对支撑布置方案进行优化对比分析,而不是简单地采用消能减震产品生产厂家提供的布置方案,并应尽可能对大震动力弹塑性分析结果进行优化,以使减震结构在满足规范要求的前提下更合理、更经济。
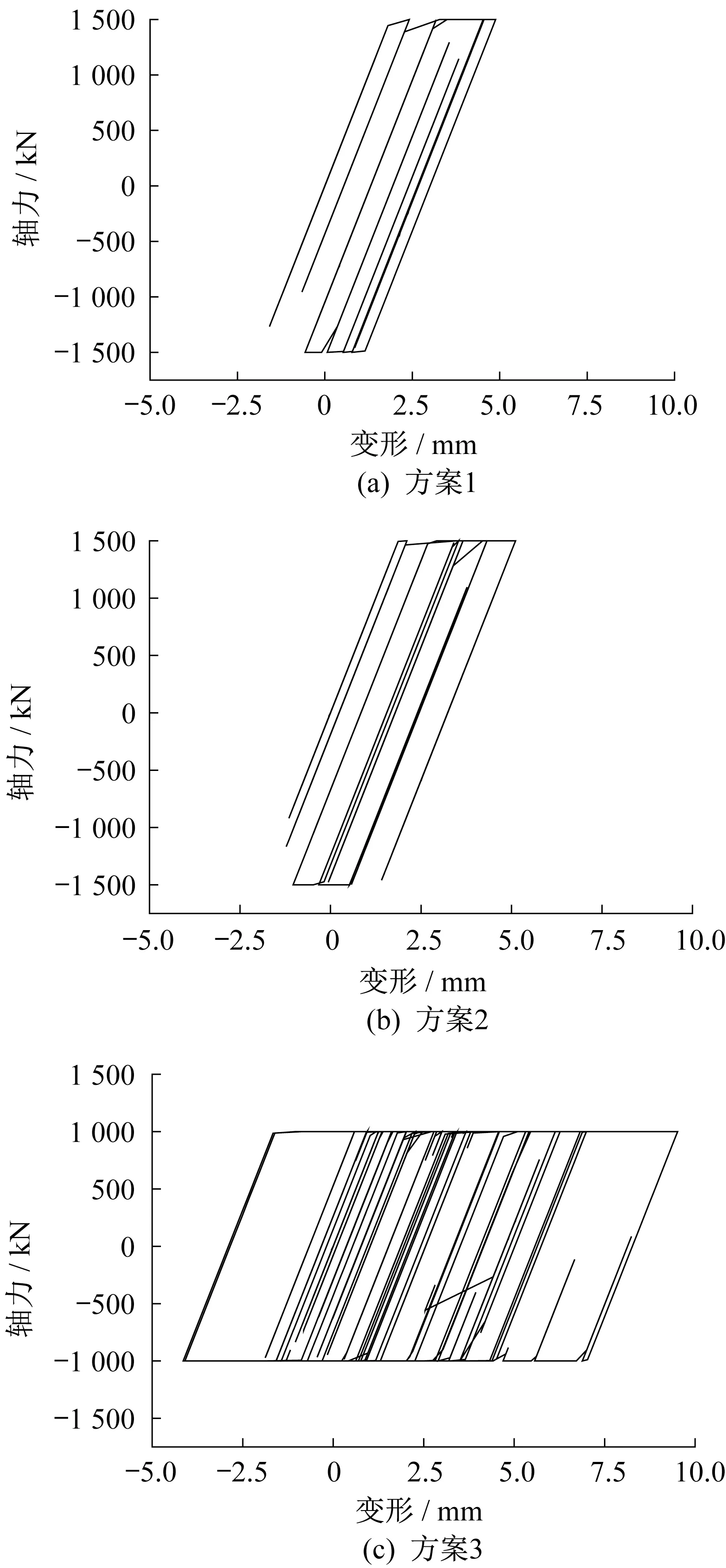
图6 各方案提取的阻尼器支撑滞回曲线Fig.6 The brace that hysteretic curve was extracted of each scheme
6 结 论
本文针对某实际工程中一减震结构的设计方案进行对比分析,得出以下结论和建议:
(1)多遇地震作用下结构反应谱分析表明,对于位移角来说,带阻尼器支撑数目的增加及其屈服力的提高并不总是有利的。
(2)多遇地震作用下结构动力弹性时程分析表明,减少了阻尼器支撑数量并降低了部分阻尼器支撑屈服力后的方案三的位移角没有明显增大,且其框架部分基底剪力是三个方案中最小的。
(3)罕遇地震作用下结构弹塑性时程分析表明,减少了阻尼器支撑数量并降低了部分阻尼器支撑屈服力后的方案三的位移角没有明显增大,且其基底总剪力与框架部分基底剪力均是三个方案中最小的,因此方案三不但在大震作用下框架部分的安全性更好,且在造价上也优于方案一与方案二。
(4)对于减震结构的设计,并不只是简单考虑增加阻尼器支撑数目、提高阻尼器支撑屈服力即可,支撑刚度的增加也可能会引起地震力的提高而导致楼层位移角变大,因此实际工程中宜根据结构楼层刚度分布情况,合理布置支撑。
(5)通过对该结构进行的小震反应谱分析、小震动力弹性时程分析及大震动力弹塑性时程分析可以看到,减震结构的优化设计对结构至关重要。
(6)方案三的滞回曲线非常饱满,在耗能能力上优于前两个方案,因此实际工程设计过程中,宜针对不同楼层选择阻尼器支撑的屈服力,如在上部楼层适当减小支撑的数量及屈服力,并结合大震动力弹塑性分析后的结果对阻尼器支撑的耗能情况进行优化。
(7)由于小震作用下的部分分析结果的规律性与大震时较为接近,故实际的减震结构设计过程中,设计师应充分利用结构设计概念,在小震下对支撑布置方案进行优化对比分析,尽可能对大震动力弹塑性分析结果进行优化,以使减震结构经济合理。
