铁道车辆轮轴全尺寸疲劳试验的原理性偏差研究

韩 立

(中国铁道科学研究院 研究生院，北京 100081)

铁道车辆轮轴作为车辆走行部的关键部件，直接关系到车辆运行安全，始终是铁路部门关注的重点[1]。轮轴疲劳强度是轮轴可靠性的最直接、最关键的指标[2]，轮轴全尺寸疲劳试验是新产品、新厂家、新材料等进行轮轴研发、检验、认证普遍要进行的关键步骤，国内外的轮轴标准体系均对此进行了规定，欧洲标准体系是目前世界上比较完善的体系，国内现行机车、客车、货车、动车组轮轴标准体系多参照欧洲标准体系的模式进行规定和运行，涉及到设计、制造、试验、认证等多个方面[3-4]，其中关于轮轴全尺寸疲劳试验的多种试验台有规定，但对试验方法的规定大多只规定试验部位应力和循环次数，对于试验过程中试验应力的确定方法无规定，且试验台的原理有所不同，故不同机构由于试验原理的理解不同和试验应力的确定方法不一致会导致试验结果有较大偏差，标准规定了两种国内外普遍采用的旋转弯曲式试验台和偏心激振式试验台，其中旋转弯曲式试验台原理比较直观，即基于悬臂梁车轴的旋转加载模式，而偏心激振式试验台，基于激振悬臂梁车轴的一阶模态加载，两者试验原理有明显的本质区别，但国内外对于这两种试验台的原理差别无系统研究，在利用偏心激振式试验台进行轮轴全尺寸疲劳试验时，其上被激振的车轴试样的一阶模态与悬臂梁车轴旋转加载方式下的应力分布差别一直是试验人员关注的重点，关系到试验应力确定精度的关键问题，直接影响疲劳试验结果[5-7]。

1 国内外轮轴标准体系中关于轮轴全尺寸疲劳试验的内容

轮轴全尺寸疲劳试验验证轮轴部件的疲劳强度，与轮轴设计方法联系密切，本节对国内外标准体系中关于轮轴全尺寸疲劳试验的内容进行梳理分析，由于国内现行轮轴标准体系多参考欧洲标准，故对于欧洲标准体系进行详细介绍。对于全尺寸疲劳试验，欧洲标准的主要思路是通过轮轴的设计评定标准(EN 13103、EN 13104、 EN 13979-1等)指导车轮、车轴设计，保证车轮、车轴结构设计，通过产品标准(EN 13260、EN 13261、EN 13262等)中的全尺寸疲劳试验验证制造商的材料、热处理工艺和机加工工艺等是否符合欧洲标准要求，设计评定标准和产品标准成体系运行保证设计-制造的闭环验证，产品标准中规定了产品应该具备的性能指标和试验验证方法，这些指标又来源设计评定标准的制定思路和与之形成呼应，标准成体系运行，国内也参考此类标准制定体系，表1、表2为国内外轮轴全尺寸疲劳试验的相关标准梳理，试验装置示意图如图1所示。

表1 国内外车轮全尺寸疲劳试验相关标准[8，13]

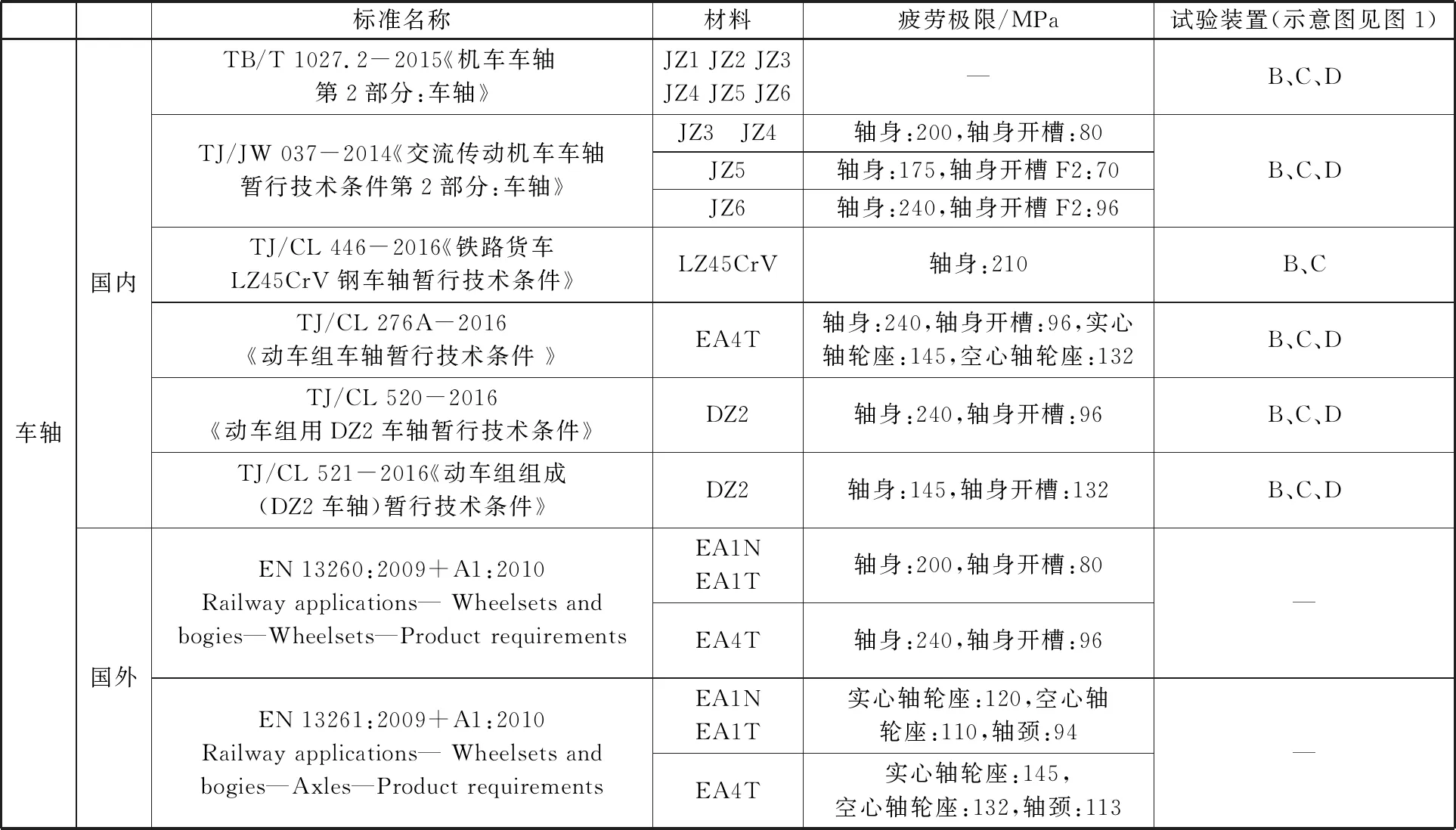
表2 国内外车轴全尺寸疲劳试验相关标准[14-21]

由表1、表2和图1可知，目前现行国内外轮轴全尺寸疲劳试验标准中关于验证轮轴疲劳强度的试验台主要有4种结构型式，在国内外最初进行轮轴全尺寸疲劳性能研究时，采用的是ABD 3类试验台,其中A类试验台只能进行车轮试验，BD类试验台(旋转弯曲式试验台)可用于车轮和车轴疲劳试验，其原理较直观，基于悬臂梁或简支梁静力弯曲变形的受力加载方式，从结构受力角度进行对部件的的性能进行验证，而C类试验台(偏心激振式试验台)是近年来出现且被越来越广泛使用的试验台，可用于车轮和车轴疲劳试验，其原理是基于偏心激振车轴试样的一阶模态加载方式，将车轴试样视为悬臂梁结构。标准中规定了车轮和车轴两种部件的试验要求，对于车轮试验，国内外一般采用利用有限元软件计算最大应力位置，并在此处及附近区域粘贴应变片，对试验部位应力直接监控，对于这4种结构型式的试验台进行车轮疲劳试验的试验应力确定过程中不存在原理性差别；而对于车轴试验，由于车轴轮座部位(轮轴过盈装配区域)无法直接粘贴应变片和车轴试验部位一般存在过渡圆弧导致的应力集中，在欧洲标准体系的规定下不适用于在试验部位直接粘贴应变片进行试验，故一般采用在试验部位一定距离的车轴轴向区域均布至少2组粘贴应变片，监控其应力值，进行线性插值以确定试验部位的应力值。对于车轴疲劳试验的“线性插值”问题，采用旋转弯曲式试验台基于悬臂梁受力的方式，有材料力学知识可知其符合应力试样沿车轴试样轴向应力分布线性的假定，不做过多的研究，而采用偏心激振式试验台时，其一阶模态下的车轴应力沿轴向分布的规律与线性假定有差别，故利用C类偏心激振式试验台进行车轴疲劳试验时的原理和偏差进行了仿真分析和试验验证研究，以期为标准体系下进行车轴疲劳试验的应力确定提供参考依据。

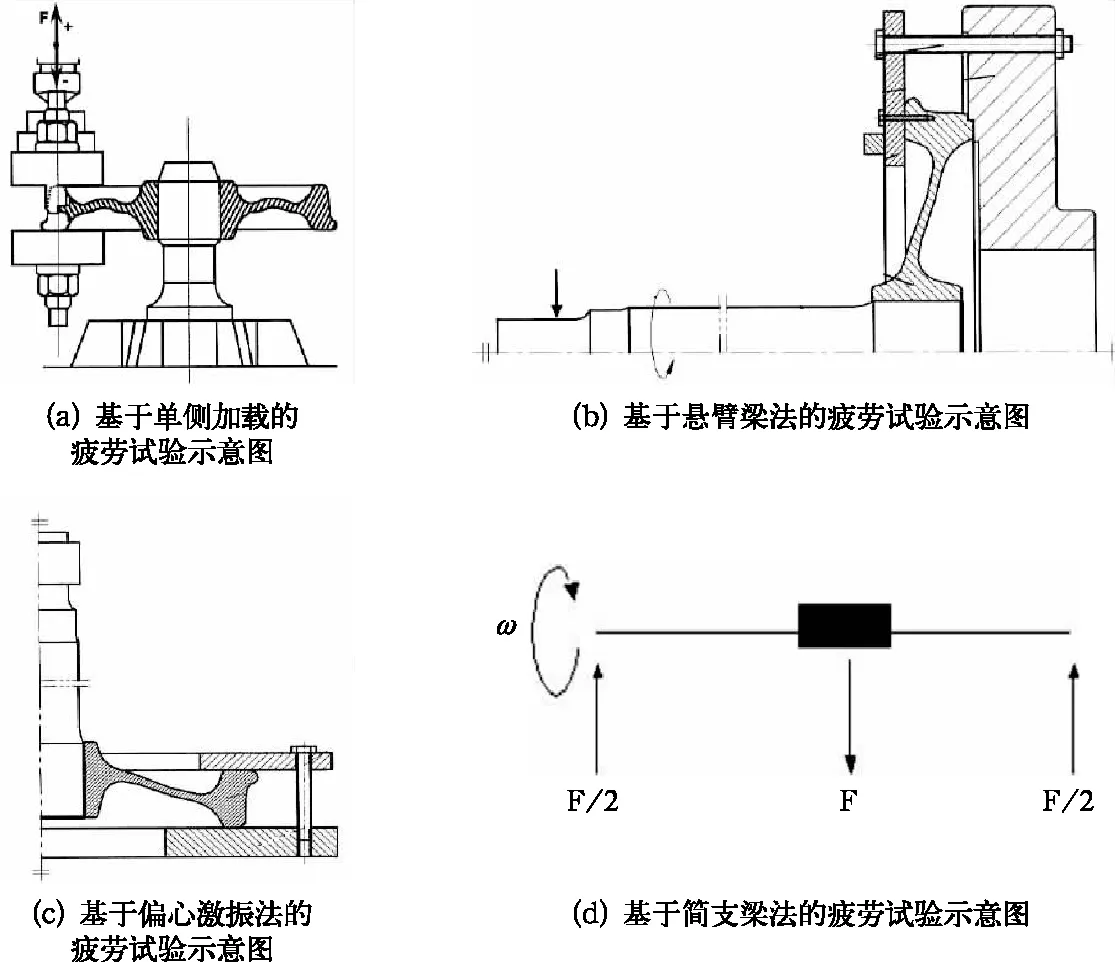
图1 试验装置示意图

C类偏心激振式试验台是基于共振原理设计的轮轴疲劳试验台，结构如图2所示，其在国内外广泛运用于全尺寸车轮、车轴的疲劳试验。其主要工作原理为，将试样一端固定于基础块上，另一端连接于激振器，激振器内部有偏心质量块，电机带动偏心质量块旋转，当电机转速接近试样的一阶共振频率时，试样被激振并按照一阶振型振动，使试验部位达到所需的试验应力。

1-电机;2-偏心激振器;3-位移传感器;4-夹持装置;5-抗震基础块;6-弹簧。图2 偏心激振式轮轴疲劳试验台结构图

偏心激振式轮轴疲劳试验台相较于在试样轴端采用液压作动器加载的传统试验台(旋转弯曲式轮轴疲劳试验台)，无需配备相关的油源、冷却设备，节能效果显著，结构紧凑、维护方便。但旋转弯曲式轮轴疲劳试验台的原理是基于静力加载下的悬臂梁变形，而偏心激振式轮轴疲劳试验台的原理是基于激振试样的一阶振型，两者在试验加载原理方面有显著差异。在使用偏心激振式轮轴疲劳试验台进行车轴疲劳试验时，一些问题仍不够清晰，如车轴在一阶振型下和静力变形下的应力分布区别、安装于试验台上的车轴试样的共振模态等，这些问题直接影响着轮轴疲劳试验过程中的参数如何选取和控制。以车轴试验为例，利用有限元软件分析了偏心激振式轮轴疲劳试验台上的车轴试样的模态、频响和应力分布结果，并对应力分布进行了试验验证。

2 偏心激振式试验台上进行车轴试验的仿真分析

在偏心激振式轮轴疲劳试验台上进行车轴试验时，一般在车轴试验部位的一侧沿轴向粘贴至少两组应变片作为确定试验部位应力的实测点，试验部位的应力线性插值确定。试验开始后，预先利用试验台自带的横向液压加载装置在车轴试样顶部加载以验证应变片测试值和梁理论计算值的符合性，之后进行试验应力确定的关键步骤，开动偏心激励器的电机，使电机转速逐渐接近车轴试样的一阶共振频率，共振频率随车轴直径的增大而增大，试验频率一般在25 Hz上下，监控应变片的应力值，利用两组应变片的测试应力值进行线性插值得到试验部位的应力值，并以此应力进行试验，直到达到要求的应力循环次数，试验结束后查看试验部位有无疲劳裂纹，以确定疲劳试验的通过与否。

在上述试验过程中，安装于试验台上的车轴试样可简化为悬臂梁模型，即一端固定、另一端加载，试验部位的应力值依赖于试验部位附近的两组应变片测试值的线性插值，即认为车轴上应力沿轴向分布为线性变化的，但研究表明在悬臂梁的一阶振型被激振状态下，其轴向应力分布并非严格的线性关系。

2.1 模态分析

由于偏心激振式试验台激振车轴试样的一阶模态进行加载，为了研究其上车轴试样的模态特征，本节车轴试样在偏心激振式试验台上的本构关系进行分析，对车轴试样的边界条件进行合理简化，采用有限元软件进行了车轴试样的模态分析。采用实体单元建立车轮、车轴模型；为避免轮轴之间过盈压装后对车轴根部应力的影响，轮轴采用耦合在一起的方式建模；车轴顶部采用点单元来建立质量点，质量点单元与车轴轴颈建立刚性区域来模拟偏心激励装置安装于车轴顶部的情况；车轮轮辋位置全约束，模拟试样安装于试验台上。如图3所示。

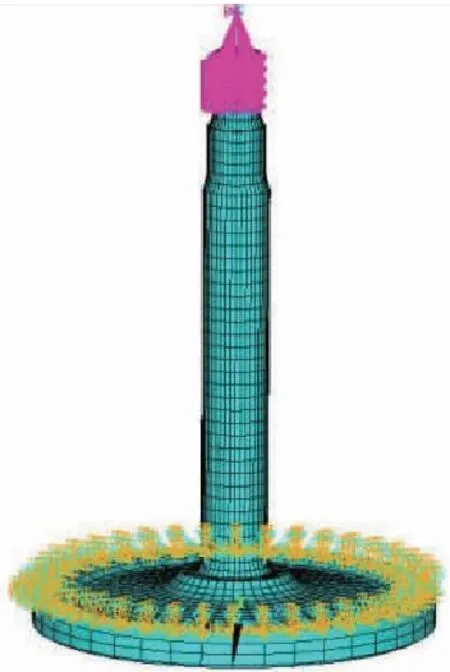
图3 有限元模型

安装于试验台上的车轴试样前六阶模态计算结果，如表3和图4所示。

表3 车轴试样模态频率

由表3和图4可知，车轴试样的一阶模态振型为车轴顶部变形量最大，向下依次减小，更高阶的模态出现车轴的中部弯曲和周向伸缩振型，与车轴试验所要求的模态振型差别较大；车轴试样的一阶模态振动频率为24.615 Hz，这与实际试验过程中偏心激振式轮轴疲劳试验台上偏心激振电机的转速较为接近，验证了偏心激振式试验台利用激振车轴试样的一阶模态进行试验的原理和模态计算结果的可靠性；车轴试样的一阶模态振动频率为24.62 Hz，二阶模态振动频率为185.84 Hz，两阶模态频率之间为7.55倍，在进行车轴试验过程中可以较好的避免两阶模态振型之间的干扰，使车轴在纯一阶模态下进行试验提供了较好条件。

图4 车轴试样前六阶模态振型

2.2 谐响应分析

在模态分析的基础上采用模态叠加法进行了谐响应分析，从而确定车轴试样在持续的周期性(随时间成正弦或余弦变化)载荷作用下持续的周期性响应(稳态响应)。将静力加载状态下的有限元计算结果与谐响应分析下的结果进行对比。对车轴试样进行谐响应分析，求解了一阶模态频率附近的节点谐响应位移解，如图5所示。

图5 谐响应分析下的节点位移解(一阶)

由图5可知，车轴试样在24.615 Hz的共振频率附近发生了共振，且共振区范围较窄，约在1 Hz左右。

2.3 应力计算结果对比

车轴试样在偏心激振式轮轴试验台上利用的激振车轴试样的一阶模态振型进行试验，车轴变形和应力分布与悬臂梁静力加载下的变形应有区别，而国内外在进行此类车轴试验时仍同等采用悬臂梁加载下应力沿轴向线性分布的基本假定，即符合欧拉-伯努利梁模型静力变形下的线性梁理论，并以此进行线性插值确定试验应力，会导致试验应力的误差。本节利用有限元方法研究车轴试样在激振其一阶模态振型下和静力加载变形下的应力分布沿车轴轴向的区别，以获得在偏心激振式轮轴试验台上进行试验的车轴试样沿轴向应力分布相对于线性分布规律的差异性，如图6所示。

图6 车轴试样有限元计算应力结果对比

由图6可知，有限元方法计算得到一节模态振型与静力加载变形下的车轴试样应力分布有差别。在车轴试样底部应力相同的情况下(可视为车轴试验轴身部位所要求达到的试验应力)，车轴试样其他部位在一阶振型下的应力小于静力变形下的应力，两者顶部最大偏差为15%；由图6中的拟合多项式可知，在同样采用二次多项式拟合应力分布曲线的前提下，车轴试样在静力变形下的应力拟合二次多项式的二次项系数为-6×10-5，二次项基本可忽略，因此车轴试样在静力变形下的应力分布曲线呈线性，可以理解为符合欧拉-伯努利梁模型的线性梁理论；但在一阶振型下的应力拟合二次多项式的二次项系数为0.0152，即车轴试样在一阶振型下应力呈非线性分布，故在偏心激振式轮轴疲劳试验台上基于车轴的一阶振型来做试验时，采用线性插值法确定试验部位应力的过程中会带来误差。

3 试验验证

3.1 试验目的

如前所述，偏心激振式轮轴试验台上进行车轴试验时是激振车轴试样的一阶模态振型进行试验，而一阶模态振型和静力加载变形下应力沿轴向分布有差别，故在理论和仿真分析的基础上，针对实际试验过程中采取的在试验部位附近粘贴应变片后进行线性插值确定试验应力的国内外惯行方法(亦是现阶段标准体系下必须采用的、较成熟的方法)，进行试验验证车轴试样在偏心激振式轮轴疲劳试验台上的应力分布是否符合线性规律和有限元分析结果，通过试验对比车轴试样在一阶模态振型和静力加载变形下的应力分布差别，对比欧拉-伯努利线性梁理论的应力沿轴向线性分布的基本假定，定量分析试验过程中因“线性插值”试验方法所带来的误差，以对试验过程中应注意的问题和试验方法改进提供依据。

3.2 试验方法

在车轴试样轴身上沿轴向分别距离试验部位100 mm、200 mm、300 mm、400 mm、600 mm、800 mm共6个截面，每个截面相隔90°两个径向方向分别粘贴应变片，组成半桥进行测试，如图7所示。利用偏心激振式轮轴疲劳试验台自身的横向力加载单元进行静力加载和偏心激振电机旋转加载产生车轴试样一阶模态振型两种加载模式，验证静力加载和一阶模态振型下的实测应力分布差别。

图7 车轴试验应变片粘贴位置

3.3 试验结果

两种加载方式下车轴应力测试结果如表4所示，在两种加载方式下，车轴试样上各点实测应力有差别，这是因为偏心激振式轮轴疲劳试验台上的横向加载单元的加载位置和偏心激振器的激振质心的高度不同导致的。

车轴试验一般利用两个截面上的实测应力进行线性插值得到车轴试验部位的试验应力，故车轴试样在两种加载模式下线性插值得到的试验部位应力结果是影响试验的关键因素，表5为车轴试样应力线性插值结果对比。

由表4可知，应变片实测应力结果和有限元计算结果线性插值得到的试验部位应力规律和偏差基本一致，也证明了有限元分析结果的可靠性。由表5线性插值结果可见，不同贴片位置在静力变形下采用线性插值得到的试验应力结果偏差较小，为0.2%，在一阶振型下的采用线性插值得到的试验应力结果偏差较大，为2.0%，应变片粘贴位置距离试验部位越远，插值确定的试验应力越小，即比试验部位的真实应力小的越多，这会导致试验过程中车轴试验部位所承受的真实应力偏大，加剧发生疲劳破坏的风险；在偏心激振式轮轴疲劳试验台上做试验时，贴片位置距离试验部位0.4 m以内线性插值得到的试验应力偏差较小，为0.4%；对于偏心激振式轮轴疲劳试验台(基于一阶振型)，选取车轴上相近的两点应力进行线性插值得到试验部位应力的过程中，有限元谐响应分析结果插值得到的试验应力最大偏差为1.9%，实测应力结果插值得到的试验应力最大偏差为2.0%，可见有限元谐响应分析结果与实测应力结果较为接近。

表4 两种加载方式下车轴应力对比

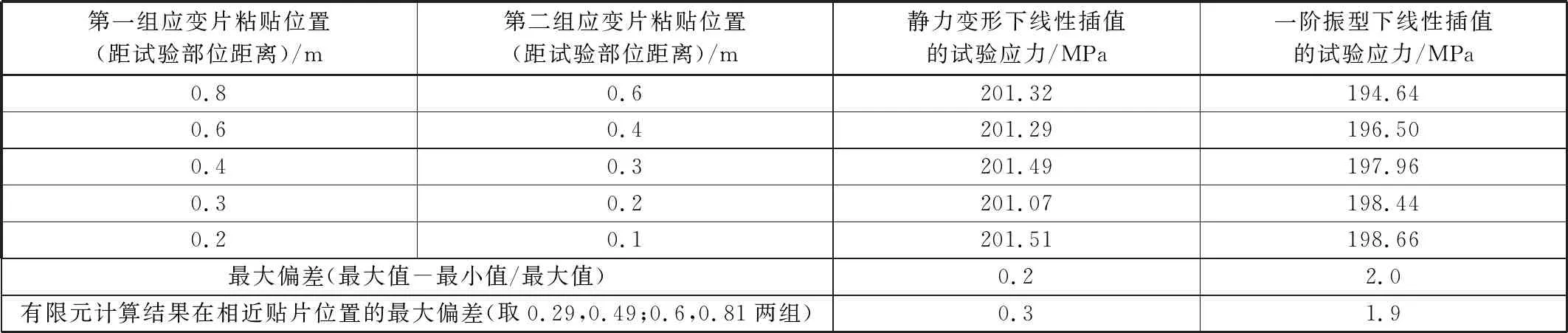
表5 车轴试样试验部位应力线性插值结果对比

4 结 论

针对国内外现行标准体系下进行的轮轴全尺寸疲劳试验的主要内容进行了梳理，针对偏心激振式轮轴疲劳试验台上进行车轴试验可能会导致的误差进行了仿真分析和试验验证，主要结论如下：车轴试样在偏心激振式轮轴疲劳试验台上进行试验时，车轴试样在一阶振型下的应力分布是非线性的，故用线性插值法确定试验部位应力时定会存在一定偏差；文中的车轴试样的一阶模态振动频率为24.615 Hz，一二阶模态频率差别较大，可以较好保证在车轴试样在一阶模态振型下试验；试验证明应变片的粘贴位置和间隔对偏心激振式轮轴疲劳试验台上的车轴试样应力确定影响较为明显，建议可将应变片粘贴于距离试验部位0.4 m以内的位置，两组应变片的粘贴间隔小于0.3 m。