低复杂度的串行抵消信道估计算法

王小军,张 凯

(西安烽火电子科技有限责任公司,陕西 西安 710075)

0 引言

随着通信系统的迅猛发展以及互联网在国民生活中的普及，人们对通信的需求正在发生变化，从最初的语音通话逐渐向无线高速数据传输以及综合业务方向发展。为此很多学者对如何提高频谱效率和可靠性方面进行了重点研究，例如具有高频谱效率的连续相位的解调算法[1-2]以及被制定为5G通信标准的极化(Polar)码[3]、低密度奇偶校验(Low Density Parity Check,LDPC)码[4-5]等。这些大多是基于理想高斯信道基础上展开的，并没有考虑多径信道对通信系统的影响以及如何对信号所处环境进行估计。

多径信道是指信号经多条路径到达接收端，接收端收到的是不同路径信号的叠加，会造成码间干扰(Inter Symbol Interference,ISI)[6]。同时由于各条路径具有不同的时延，从时域上会造成信号的弥散，从频域上会造成频率选择性衰落，这些由多径传输带来的影响统称多径效应[7]。多径效应会使通信系统的性能恶化，因此在传输信息前必须对信道进行估计。信道估计是所有通信系统首要面临的问题，同时也是建立通信的基础。现有信道估计的算法主要采用导频信号[8]，例如最小均方算法(Least Mean Square,LMS)和递归最小二乘法(Recursive Least Square,RLS)。这些算法非常简单，但当选取的参数不匹配时会产生振荡、不收敛的现象[9]。还有一种算法不采用导频信号，这种算法称为盲估计算法[10]。盲估计算法相比于基于导频信号的缺点是算法复杂、收敛速度慢，同时受到信道环境、噪声等其他因素的影响较大[11]。

随着Turbo码[12]的发现，人们将Turbo译码算法中的迭代思想引入到通信系统中，使得系统性能得到显著提高。例如Turbo均衡[13]就是利用了迭代的思想，信息在均衡器和译码器之间反复迭代，直至译码成功或达到最大迭代次数为止。借鉴Turbo译码策略，可以将迭代的思想引入信道估计中。本文针对信道估计引入了先验信道信息和信道外信息的概念,并在此基础上提出了串行抵消信道估计算法,最后结合实际的通信系统对其性能进行了仿真。

1 符号定义与系统模型

1.1 符号定义

假设多径信道冲击响应h=(h-p,h-p+1,…,h-1,h0,h1,…,hq)。其中，主径(能量最强的)为h0，hi(i<0)为主径之前的路径，表示先于主径信号到达接收机，hi(i>0)为主径之后的路径，表示晚于主径信号到达接收机。待传输的长度为k的二进制训练为x=(x0,x1,…,xj,…,xk-1)，(xj∈±1)。考虑到信道多径的影响,传输前在训练序列x的前后添加保护带,添加了保护带的训练序列为X=(x-l1,x-l1+1,…,x-1,x,xk,…,xk+l2-1),其中(x-l1,x-l1+1,…,x-1)是长度为l1的前保护带，(xk,…,xk+l2-1)是长度为l2的后保护带，l1≥q，l2≥p。

1.2 系统模型

接收端收到的信号为信道冲击响应h与带有保护带的训练序列X的卷积。第j时刻的接收值的表达式为：

rj=h-pxp+j+h-p+1xp-1+j+…+h-1x1+j+h0xj+

h1x-1+j+…+hqx-q+j+wj,

0≤j≤k-1，

(1)

式中，wj为服从均值为0、方差为σ2的正态分布的采样值。

将式(1)采用矩阵表达，其形式如下：

(2)

为了简单起见将式(2)写作R=H·X+W。其中，R为实际接收向量，维数为k×1，H为实际信道位移矩阵，维数为k×(p+q+k)；X为待传输的训练序列向量，维数为(p+q+k)×1；W为服从均值为0、方差为σ2的正态分布噪声向量，维数为k×1。

信道参数估计的目的是利用R与已知的X来估计h中每个元素的数值，以及叠加的高斯白噪声的方差。

2 估计原理

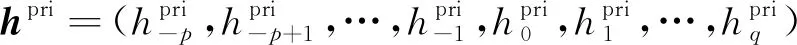
先验信息是指在估计前已掌握的关于信道的部分信息，此信息可能不准确。现在需要利用Hpri得到更加精确的信道估计值。下面以估计分量ht(-p≤t≤q)为例详细说明估计原理。

3.计算实际接收值与模拟接收值的差值向量：

(3)

即

⋮

⋮

3 信道估计算法

3.1 串行抵消算法

对于1.2节给出的系统模型，利用信道先验信息hpri和接收值R获得第t条信道外信息的串行抵消算法如下：

3.计算差值向量Dht=0=R-Rht=0;

3.2 信道估计迭代算法

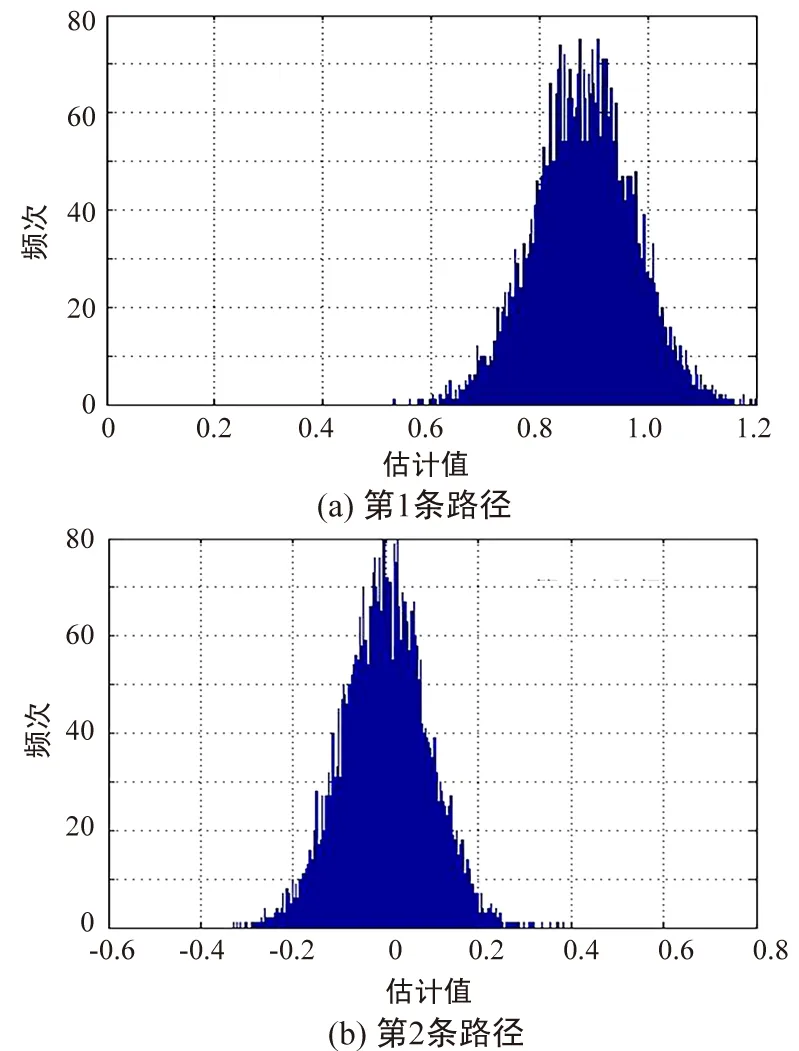
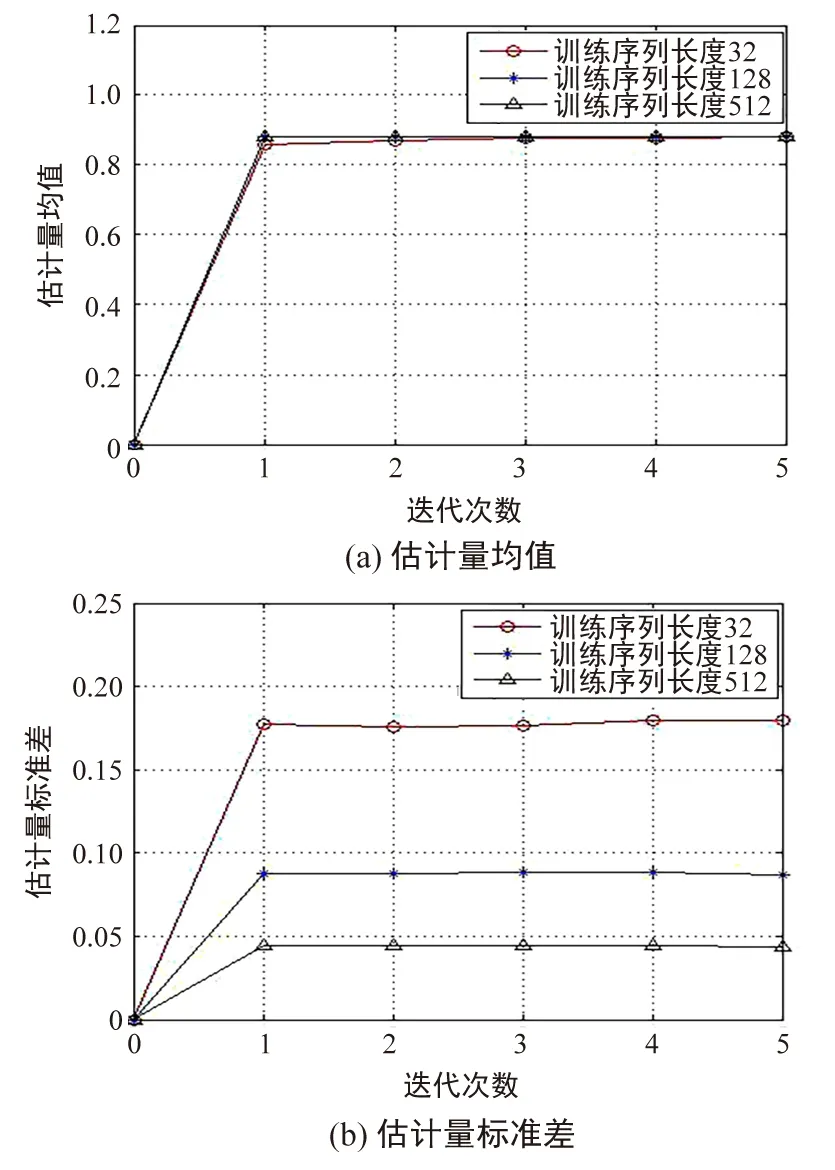
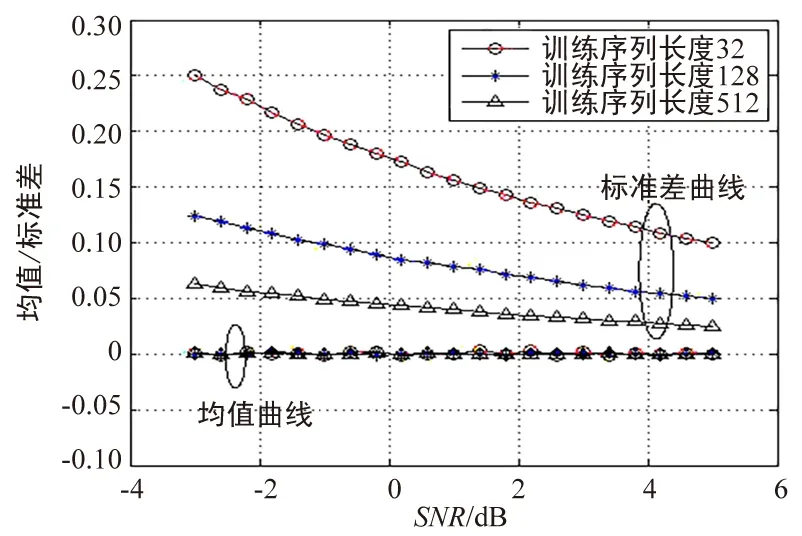
1.当l

2.令路径索引变量t=-p，并执行以下步骤：

b.变量t加1。若t>q，则进入步骤3；否则进入步骤2a。

4.将外信息作为新的信道先验信息hpri=hext，迭代次数变量l加1。

5.若l不等于L，进入步骤1，否则进入步骤6。

需要说明的是：在没有达到最大迭代次数时，总是将本次迭代得到的信道外信息hext作为下一轮迭代的信道先验信息hpri；当到达最大迭代次数时，将本次迭代得到的外信息作为最终估计结果。初始时刻不论先验信息hpri为何值，经过有限次迭代后总能够收敛于稳定点；然而在初始时刻信道，估计器不了解关于信道的任何信息，因此通常将先验信息设置为全0，即hpri=(0,0,0,0,…,0)。

3.3 信道噪声方差估计算法

4 复杂度分析

从上一节可知，本文提出的串行抵消信道估计算法采用迭代的方式逐渐逼近信道的真实特性，每次都会将上一次的估计值作为本次的先验信息，同时利用已知的训练序列再一次对信道进行估计，每一次的估计结果都会比上一次更加精确。从算法的过程可以看出，每次对信道估计的复杂度都是相同的，因此为考察算法的复杂性，可以重点分析每次迭代所需的计算量。

对于相同的参数，若采用LMS算法，对所有信道进行估计则需要2k(p+q+1)次乘法和k(p+q+1)次加法。表1给出了串行抵消算法和LMS算法的计算量。

表1 串行抵消算法与LMS算法的计算量Tab.1 Computational of serial cancellation and LMS algorithm

5 性能仿真

5.1 信道估计量的分布

由于信道估计量是一个随机变量，每次估计出的数值不相同，有的可能非常接近真实值，有的可能背离真实值。在给定信噪比的情况下，将N次试验结果进行统计并绘出直方图，进而考察估计值的分布情况。仿真参数为：训练序列长度为128的m序列；令信道估计迭代算法迭代最大次数10；试验次数N=10 000。图1给出了在SNR=0 dB时，第1条(真实值为0.880 5)和第2条(真实值为0)路径估计值的分布情况。

图1 路径估计量分布情况Fig.1 Distribution of path estimator

从图1中可以看到,各路径参数估计量的分布特性如高斯分布，因此可以使用均值和标准差两个参数来刻画此随机变量。例如第1条与第2条路径参数估计量的均值为0.880 5,0.000 7,说明这种迭代的估计算法为一致性估计。估计量的标准差分别为0.087 9,0.088 0。

需要指出，对于时变信道，串行抵消算法虽然不能实时跟踪信道的变化，但是在较短的时间范围内可以认为信道的改变量不大，近似的将其看作恒定信道[13]，则采用串行抵消算法估计出的信道特性应为这一段时间内信道的平均值。

5.2 估计量统计特性随迭代次数变化

以第1条路径为例，图2给出了在SNR=0 dB时，训练序列长度分别为32,128,512的收敛特性。从图中可以看出信道估计迭代算法具有快速收敛特性，仅需要1次迭代基本就趋于稳定，且训练序列越长估计的精度就越高。

图2 不同长度的训练序列Vs估计量均值和标准差Fig.2 Training sequences of different lengths VS estimator mean and standard deviation

5.3 不同信噪比下估计的精度

图3以第2条路径(真实值为0)为例，给出了不同信噪比下采用不同长度的训练序列进行信道估计的统计结果。从图中可以看到:

① 不论训练序列长度为何值，其估计出的参数均值基本相同。

② 估计出的标准差具有不同的特性，训练序列越长，估计的精度越高。例如在-3 dB训练序列长度为32时，估计出的信道参数标准差为0.250 2 ；长度为512的情况下估计出的信道参数标准差为0.062 8。

③ 随着信噪比的增加，不同长度训练序列下的估计精度均逐渐提升。

图3 不同信噪比下估计量的统计特性Fig.3 Statistical characteristics of estimators under different SNR

5.4 参数估计迭代算法在Turbo均衡中的性能

考察了信道参数估计迭代算法在Turbo均衡中的性能，时域Turbo均衡算法采用文献[14]中介绍的方法。训练序列选取长度分别为128和512的m序列，信道估计的迭代最大次数2。LDPC码选取码率为0.25的(1 060,265)[15],译码迭代次数50。Turbo均衡中联合迭代次数为5。同时为了进行对比，还给出了真实信道下的性能曲线。仿真性能如图4所示。

图4 不同长度的训练序列在Turbo均衡中的性能Fig.4 Performance of training sequences with different lengths in Turbo equalization

从图4中可以看出，串行抵消信道估计算法在时域Turbo均衡中能够起到对信道估计的作用，且训练序列长度越长，则其性能越好。例如当BER=10-5时，精确估计所需的信噪比约为-0.6 dB，采用训练序列长度为512的信道估计算法所需信噪比约为-0.45 dB，而训练序列长度为128的信道估计算法所需信噪比约为0.2 dB，二者与精确估计分别有0.15 dB和0.8 dB的性能差异。

6 结束语

本文提出了低复杂度的串行抵消信道估计算法，发送端发送一段收发双方均已知的训练序列，接收端对收到的训练序列进行迭代处理。估计算法基于信道的先验信息来提取指定信道参数，并在已估计出的参数基础上，再次使用串行抵消信道估计算法，每次迭代后估计出的信道参数作为下一次迭代的先验信息，以迭代的方式来进一步逼近信道的真实特性；随着迭代次数的增加，估计出的参数精确度逐渐提高。仿真结果表明，提出的串行抵消信道估计算法能够非常准确地对信道进行估计，且具有简单、快速收敛、易于工程实现等优点。在Turbo均衡系统中该算法能够准确地对信道进行估计，其性能与真实信道仅有0.15 dB的差距。