基于参量下转换的量子纠缠光源仿真模型

周 政，安雪碧，钱泳君，陈 巍

(1.中国科学技术大学，安徽 合肥 230026；2.安徽问天量子科技股份有限公司，安徽 芜湖 241002)

0 引言

量子信息是量子力学和信息科学交叉融合的产物，也是新工科发展的重要内容之一。对量子信息的教学是相关研究和应用的基础。量子纠缠是量子信息研究的核心资源，它是量子密码[1-3]、量子隐形传态[4]及线性光学量子计算[5]等的理论和实验基础。高性能的实体量子纠缠源实验装置较为昂贵、对实验环境要求比较苛刻，可能出现损坏以及量子光信号无法可视化等问题。这些问题严重限制了纠缠光源在教学中的普及和教学效果。此前已有一些针对量子密码[6-9]、量子安全直接通信[10-12]等方案的虚拟仿真研究。其中文献[7-9]对基于参量下转换的量子纠缠光源进行了仿真。但是这些工作中对量子纠缠源的仿真都面向量子密码、量子直接通信等具体协议，并没有涉及Bell不等式的测量和分析等内容，并且主要是针对非线性晶体的特性进行模拟，没有突出量子纠缠光源和其他非线性光学器件在量子领域的特性区别。面向使用I型偏硼酸钡(BBO)晶体产生的实际纠缠光源，在充分考虑了光学器件可调节特性的前提下，对Bell不等式测试、纠缠源保真度测量以及干涉可见度测量等实验内容进行了建模，给出了双光子符合计数与可调光学器件之间的函数模型。这一方法和思路可推广用于仿真基于周期极化磷酸氧钛钾(PPKTP)晶体的其他类型量子纠缠光源，并可能用于科研级量子光学系统的设计。

1 量子纠缠和量子纠缠光源

1.1 量子纠缠态

在量子力学中，若一个系统的态空间能够使用单一的波函数或者态矢量表征，则称该系统处在纯态。纯态S可用狄拉克符号表示为|φ〉。对一个存在两粒子A,B的复合纯态系统，如果这个纯态|φ〉A,B不能表示为两个子系统的直积态|φ〉A⊗|φ〉B，则态|φ〉A,B就是一个纠缠态，即A，B两个子系统是相互纠缠的[13]。纠缠的定义可扩展到多体系统，即若整个系统处于纯态，且不能写成各个子系统纯态的直积形式，那么这个系统就处于纠缠态，所有子系统互相纠缠。

以A,B两个电子构成的总自旋为零的纯态为例，测量两个电子自旋态时，只存在两种情况：A电子自旋向上，B电子自旋向下，表示为|↑↓〉；A电子自旋向下，B电子自旋向上，表示为|↓↑〉。这两种情况不经测量无法区分，其波函数可以写为：

(1)

当对A电子进行自旋测量，将以1/2概率得到自旋向上态|↑〉，以1/2的概率得到自旋向下态|↓〉。如果测得A电子自旋向上，则B电子必然自旋向下，态|φ〉塌缩为|↑〉A|↓〉B；相反的，如果测到A电子自旋向下，则B电子必然自旋向上，态塌缩为|↓〉A|↑〉B。

1.2 量子纠缠光子对制备

双光子纠缠源的制备技术目前已较为成熟，较常用的制备方法是利用自发参量下转换(Spontaneous Parametric Down Conversion，SPDC)制备纠缠光子对[14-16]。SPDC是利用非线性晶体的二阶非线性效应。频率为ωp的泵浦光(pump)通过非线性光学介质后，产生另外两个频率为ωs,ωi的低频光，分别称之为信号光(Signal)和闲频光(idler)。SPDC过程要求低频光和泵浦光满足能量守恒和动量守恒，即需要晶体的切割角满足相位匹配条件[16]。

对于负单轴晶体，相位匹配条件要求倍频光的偏振与折射率较小的非常光(e光)相同。此时，基频光偏振的选择可以有两种：两基频光取相同的偏振(o光)，参量转换过程为e→o+o；两基频光取互相垂直的偏振态(o光和e光)，参量转换过程为e→e+o。将这两种不同的相位匹配方式分别称之为Ⅰ型和Ⅱ型匹配。由于基于I型相位匹配晶体的量子纠缠光源在实际实验中具有亮度高、不需空间补偿晶体等优点，在实验中被广泛采用，本文选取基于这种类型晶体的量子纠缠光源进行仿真建模。

利用I型SPDC制备纠缠光源，其过程如图1[16]所示，具体描述如下。

一个45°偏振的泵浦光，入射到两片粘合在一起的光轴互相垂直(晶体 #1的光轴位于垂直面内，晶体 #2的光轴位于水平面内)的BBO晶体上。按照相位匹配条件，只有在泵浦光是垂直(水平)偏振时，下转换过程才会在晶体#1(#2)中发生，产生偏振为水平(竖直)的光锥，且晶体 #1 和晶体 #2 具有同样的几率发生下转换过程。由于两片BBO晶体很薄，所以两个光锥几近重合。当在光锥上对称两点收集光子，则可以同时收到偏振同为水平或者同为垂直的光子，并且到达光子在时间和偏振态上不可预测和不可区分。但是当对其进行测量时，若一端检测结果为水平(竖直)偏振态，则另一端偏振态也瞬时确定地塌缩为水平(竖直)偏振态。

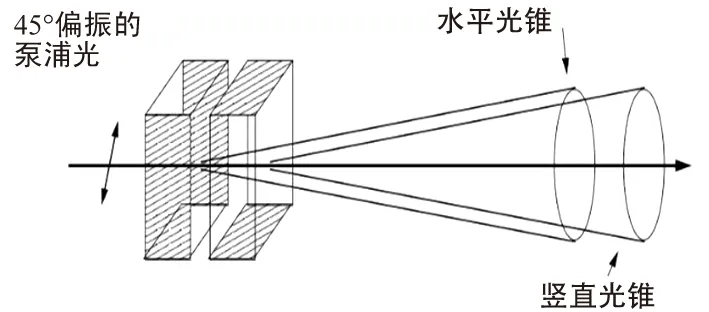
图1 I型参量下转换产生纠缠光子示意图Fig.1 Schematic diagram of entangled photons produced by type I spontaneous parametric down conversion

在这种情况下，相干叠加得到偏振纠缠态可以描述为:

(2)

调节位于 BBO 晶体前的零级四分之一波片可以改变上式中的φ，从而实现标准的Bell 态：

(3)

在其中一路上加入一块半波片，使偏振H与V互换，则可实现另外两种 Bell 态：

(4)

完整的I型BBO量子纠缠源装置如图2所示。

图2 I型BBO晶体量子纠缠源实验装置Fig.2 Experimental setup of quantum entanglement source based on type I BBO crystal

实验装置采用405 nm波长的激光器输出连续激光。经过偏振分束器PBS后，垂直偏振光V经过半波片(Half-Wave Plate,HWP)对偏振进行旋转至偏振45°。405 nm激光经过透镜Lens聚焦于图1所示结构的BBO晶体上，发生参量下转换过程后，产生810 nm纠缠光子对，两束纠缠光束夹角为3°。利用反射镜改变光路，使光束夹角变为180°后，用单模光纤分别对其进行收集并输入单光子探测器(Single Photon Detector,SPD)。SPD产生的电信号进入符合计数仪，符合计数仪可以给出两个单光子探测器在1 ns内同时接收到光子的符合计数值(由于参量下转换过程中两个光子同时产生，一般利用这个特点，使用符合计数仪来滤除噪声)。单模光纤准直器前放置滤波片用于滤除杂散光和噪声光，并加入偏振片、HWP和四分之一波片(Quarter-wave Plate,QWP)组成测量装置，可用于测量干涉可见度、纠缠源保真度及Bell不等式测试[16-20]实验。其中，BBO为β-BaB2O4晶体，OC为光纤准直器。

2 I型BBO纠缠源仿真模型

下面给出上述量子纠缠光源的仿真模型。如图2所示，泵浦光强记为p，纠缠光子对产生率为R，A、B两路本底衰减分别为ηA1和ηB1，用户调节耦合头OC1和OC2的偏转角度分别为χ1和χ2，则对应引起的衰减分别为：

ηA1=cos(χ1)，

(5)

ηA2=cos(χ2)。

(6)

符合门宽为T，其初始值为2 ns并可进行调节。两路的真实符合计数cT为：

cT=p·R·ηA1·ηA2·ηB1·ηB2·c，

(7)

式中，c为符合计数率，它由实验装置中波片、BBO晶体等角度决定，c的具体形式和推导过程如下。

激光器发出的光，经过偏振分束器PBS后，其量子态可表示为|H〉，经过角度为θ1的HWP2后的量子态为：

cos2θ1|H〉+sin2θ1|V〉。

(8)

经过角度为θ2的BBO之后，量子态为:

|ψ〉=cos(θ2-2θ1)(cosθ2|H〉+sinθ2|V〉)(cosθ2|H〉+sinθ2|V〉)+
sin(θ2-2θ1)(sinθ2|H〉-cosθ2|V〉)(sinθ2|H〉-cosθ2|V〉)=
(cos(θ2-2θ1)cos2θ2+sin(θ2-2θ1)sin2θ2)|H〉|H〉+
(cos(θ2-2θ1)sin2θ2+sin(θ2-2θ1)cos2θ2)|V〉|V〉+
(cos(θ2-2θ1)-sin(θ2-2θ1))cosθ2sinθ2|V〉|H〉+
(cos(θ2-2θ1)-sin(θ2-2θ1))cosθ2sinθ2|H〉|V〉。

(9)

设测量臂QWP1角度为φ1、HWP3的角度为θ3、QWP2的角度为φ2和HWP4的角度为θ4，则两臂测量基本征态的表达式分别为：

|U〉=[(cos2φ1+isin2φ1)cos2θ3+(1-i)cosφ1sinφ1sin2θ3]|H〉+
[(1-i)cosφ1sinφ1cos2θ3+(icos2φ1+sin2φ1)sin2θ3]|V〉，

(10)

|D〉=[(cos2φ2+isin2φ2)cos2θ4+(1-i)cosφ2sinφ2sin2θ4]|H〉+
[(1-i)cosφ2sinφ2cos2θ4+(icos2φ2+sin2φ2)sin2θ4]|V〉。

(11)

则两臂单光子探测器的符合计数率为：

C=|〈U|〈D|⊗|ψ〉|2。

(12)

先将测量基矢展开为：

〈U|⊗〈D|=[(cos2φ1-isin2φ1)cos2θ3+(1+i)cosφ1sinφ1sin2θ3]×
[(cos2φ2-isin2φ2)cos2θ4+(1+i)cosφ2sinφ2sin2θ4]〈H|〈H|+
[(cos2φ1-isin2φ1)cos2θ3+(1+i)cosφ1sinφ1sin2θ3]×
[(1+i)cosφ2sinφ2cos2θ4+(-icos2φ2+sin2φ2)sin2θ4]〈H|〈V|+
[(1+i)cosφ1sinφ1cos2θ3+(-icos2φ1+sin2φ1)sin2θ3]×
[(cos2φ2-isin2φ2)cos2θ4+(1+i)cosφ2sinφ2sin2θ4]〈V|〈H|+
[(1+i)cosφ1sinφ1cos2θ3+(-icos2φ1+sin2φ1)sin2θ3]×
[(1+i)cosφ2sinφ2cos2θ4+(-icos2φ2+sin2φ2)sin2θ4]〈V|〈V|。

(13)

由此得到符合计数率的最终表达式：

c=|〈U|⊗〈D|ψ〉|2=
|[(cos2φ1-isin2φ1)cos2θ3+(1+i)cosφ1sinφ1sin2θ3]×
[(cos2φ2-isin2φ2)cos2θ4+(1+i)cosφ2sinφ2sin2θ4]×
(cos(θ2-2θ1)cos2θ2+sin(θ2-2θ1)sin2θ2)+
[(cos2φ1-isin2φ1)cos2θ3+(1+i)cosφ1sinφ1sin2θ3]×
[(1+i)cosφ2sinφ2cos2θ4+(-icos2φ2+sin2φ2)sin2θ4]×
(cos(θ2-2θ1)-sin(θ2-2θ1))cosθ2sinθ2+
[(1+i)cosφ1sinφ1cos2θ3+(-icos2φ1+sin2φ1)sin2θ3]×
[(cos2φ2-isin2φ2)cos2θ4+(1+i)cosφ2sinφ2sin2θ4]×
(cos(θ2-2θ1)-sin(θ2-2θ1))cosθ2sinθ2+
[(1+i)cosφ1sinφ1cos2θ3+(-icos2φ1+sin2φ1)sin2θ3]×
[(1+i)cosφ2sinφ2cos2θ4+(-icos2φ2+sin2φ2)sin2θ4]×
(cos(θ2-2θ1)sin2θ2+sin(θ2-2θ1)cos2θ2)|2。

(14)

以上推导给出了符合计数率c与HWP2和BBO晶体，测量光路中的QWP1,HWP3,QWP2,HWP4旋转角度之间的关系。

带入cT的计算式(7)，可得到实际每秒的单光子符合计数。为模拟真实环境中的噪声，设每一路的单通道计数为NA=p·R·ηA1·ηA2，NB=p·R·ηB1·ηB2，随机符合计数cR为cR=NA·NB·T。综合以上模型和推导过程，可以给出最终符合计数仪输出的符合计数为cA=cT+cR。

值得注意的是，上述模型给出的是理论推导的精确值，在实际实验中，实验测量往往会受到噪声影响。因此在仿真模型中加入随机参数cR，其概率分布满足高斯型分布N(μ=1，σ2=1)。最终仿真模型给出的符合计数为cR·cA。即使波片角度等参数完全相同，每秒钟的符合计数也会出现抖动，从而进一步模拟实际实验数值受噪声影响产生的抖动。

利用上述模型，只需输入HWP2和BBO晶体，测量光路中的QWP1,HWP3,QWP2,HWP4旋转角度以及准直器OC1和OC2的偏转角度，就可以给出符合计数仪的输出数据。这一模型的输入参数与实际实验中调节器件类型和参数完全对应，从而实现对实际量子纠缠光源实验装置的虚拟仿真。

利用上述模型，可以模拟仿真利用图2实验装置进行Bell不等式测试实验[16-20]。在此采用CHSH型不等式[20]：

S=E(a,b)-E(a,b′)+E(a′,b)+E(a′+b′)。

对于经典体系，CHSH型不等式的最大值为2，当S实验值大于2时，说明实验装置具有非局域性，即存在量子纠缠。

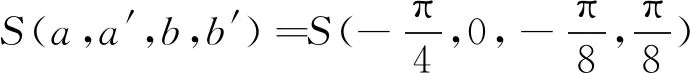
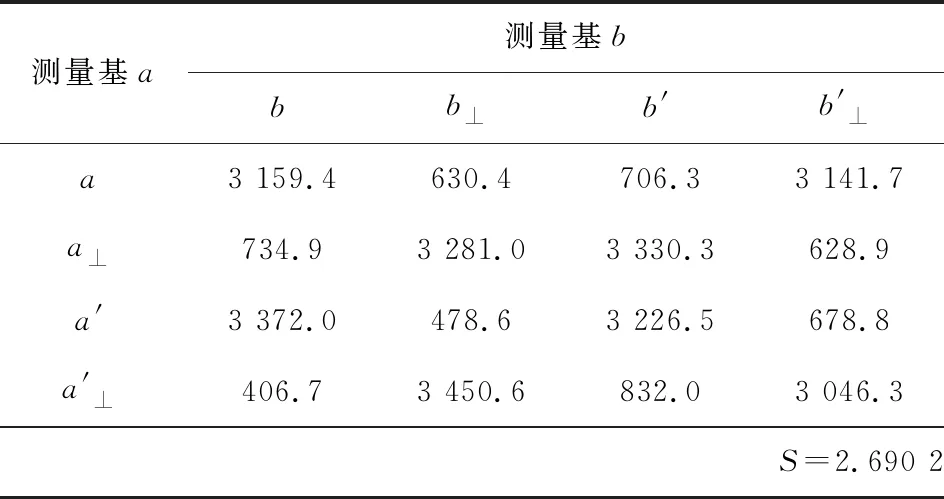
表1 Bell不等式测试实验数据，均取10 s平均值Tab.1 Experimental data of Bell’s inequality,average value in 10 s

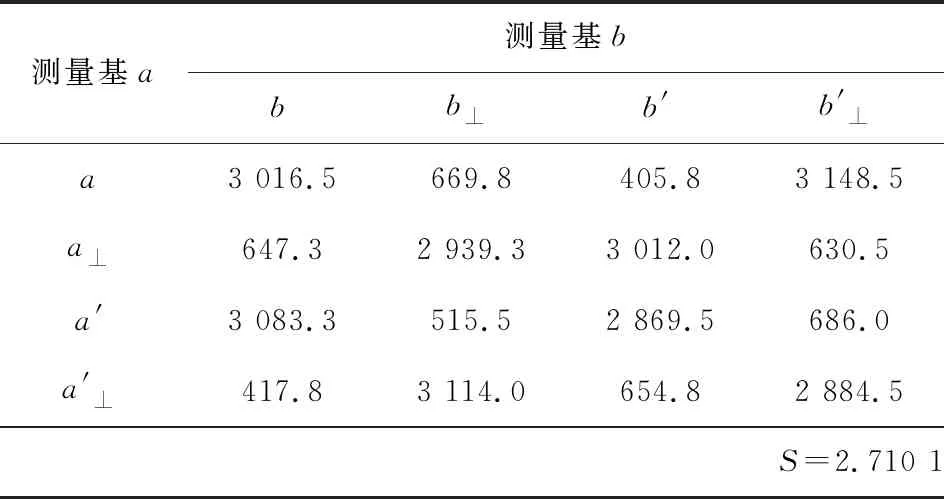
表2 Bell不等式测试仿真数据Tab.2 Simulation data of Bell’s inequality

此外，还测量了纠缠光子对的干涉曲线，即保持测量光路中QWP1,QWP2,HWP3的角度为0，旋转HWP4的快轴角度θ。实验数据和模拟仿真数据如图3所示，纵坐标为每秒符合计数，实验数据均取10 s平均值。

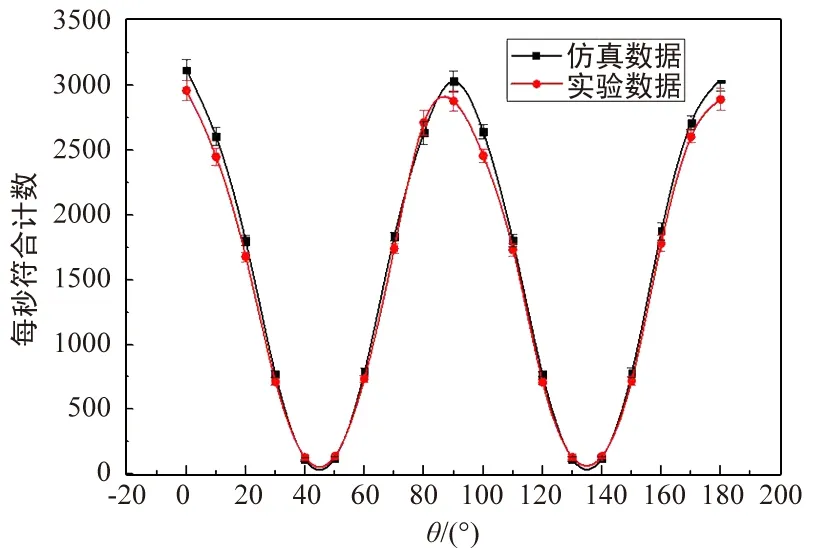
图3 仿真模拟数据和实验数据Fig.3 Simulation data and experimental data

由图3可以看出，虚拟仿真模型给出的数据更接近理论模型的三角函数曲线，真实实验数据由于有更多的噪声和误差，会比虚拟仿真实验数据有更低的干涉可见度。这可以通过调节虚拟仿真模型中的高斯噪声函数来调整，进一步逼近真实实验数据。但是由于真实实验数据会随实验室环境(温湿度、实验台面抖动)和实验装置调节状态等诸多不可控因素影响，每次测量的结果也无法完全一致，因此虚拟仿真模型只能逼近，而无法与实验数据完全一致。

3 结论

通过以上对实体I型BBO量子纠缠源的仿真模型的推导，给出了虚拟仿真模型，并将虚拟仿真模型给出的数据与实际实验数据进行了对比,该模型与实际实验数据保持了较好的一致性。可以利用本文给出的虚拟仿真模型进行Bell不等式违背、干涉可见度测量、纠缠源保真度测量等虚拟仿真实验，并且为EPR-steering[21]和经典维度目击违背[22-24]等理论研究的快速实验验证提供仿真模型和计算工具。