用于航班延误预测的集成式增量学习算法

2020-11-11王晓曦

北京工业大学学报 2020年11期

王丹，王萌，王晓曦，杨萍

(1.北京工业大学信息学部，北京 100124； 2.国家电网管理学院，北京 102200)

当今大数据时代，每时每刻都有新数据产生，其中往往包含着对后续事件预测有着重要影响的信息. 在机器学习领域，已经实现了多种用于预测的模型和算法. 因为能够持续、高效地学习新数据中包含的信息，并提高模型预测的准确率，所以增量学习技术受到了广泛关注[1]. 例如，在航班预测领域，有专家提出“对于航班预测而言，获取最新的信息并加入到预测中，会为预测准确度带来更大的提升[2]”. 一般地，越是新到达的航班的运行信息对预测结果的影响也会越大，特别是那些刚刚获得的前航班的延误情况，起飞机场、目的机场的延误情况等. 由此可见，为航班预测模型提供具有增量学习能力的算法十分符合航班预测的实际需求.

在航班预测模型构建中，文献[3-5]均是利用贝叶斯网络来建立航班延误预测模型；文献[6]采用C4.5决策树构建航班预测模型，并与目前常用的贝叶斯分类方法进行对比，证明C4.5决策树算法能进一步提高预测精度；文献[7]利用随机森林算法预测空中交通延误情况. 决策树算法目前已得到广泛应用[8]，其中，分类与回归树(classification and regression tree，CART)算法[9]是由Breiman学者提出的，它是一种基于Gini系数的二分法决策树分类算法. 由于它具有“稳定性- 可塑性灾难”的特性，为学习新到达数据，只能抛弃现有决策树，利用历史数据集构造新的决策树，所以不具备增量学习的能力. ID5算法、ID5R算法等是具有增量学习功能的决策树算法，它们常常是对原始决策树算法中的节点中存储属性信息加以改造，再利用新获得的数据不断调整原有决策树，进而达到增量学习的目标[10]. 在增量学习过程中，这类算法需要不断地借助存储的信息调整决策树的结构，因此，需要额外的存储空间，若某些参数设置不当会引发过拟合，影响分类效果[11].

考虑到集成学习方法具有高泛化性、分类效果好和增量过程相对简单的特点，本文采用集成学习思想实现了一种增量分类与回归树(incremental classification and regression tree, I-CART)算法. 该算法利用集成学习思想使得CART算法克服了“稳定性- 可塑性灾难”[12]，实现了增量学习，具备了持续学习不断到达的新数据的能力且提高了学习新信息的效率，并采用选择性集成方法对其存在的集成分类器规模庞大的问题进行了改进. 该方法充分考虑了分类器的差异性与精确度对最终集成分类器的分类效果的影响[13]，依据选择性集成理论来构建分类效果更优的基分类器子集. 同时，集成分类器规模显著减少，存储压力得以缓解，分类器预测速率得到提高.

1 I-CART算法概述

1.1 Learn++算法

采用集成学习思想的Learn++算法[12]具有适用性广、参数设置简单等优势，它将已经学习的历史数据作为基分类器加以保存且在学习新到达的数据时无须访问历史数据，当访问历史数据时也遗忘旧知识，以此方式通过不断学习新到达的数据相应生成多个基分类器，使集成分类器得到扩充.

1.2 I-CART算法

本文将CART决策树作为基分类器，将CART算法与Learn++算法相结合，采用集成学习思想设计并实现了I-CART增量学习算法，如算法1所示.

算法1 I-CART算法

输入：将原始数据集Data分为K份，标记为D(k，k=1,2,…,K)；从D(k)中随机选取数据集S，S=[(x1,y1),(x2,y2),…,(xm,ym)],i=1,2,…,m；基础学习算法为CART算法，子数据集迭代次数Tk；

输出: 集成分类器Cfinal

fork=1,2,…,Kdo

初始化样本权重:

w1(i)=D1(i)=1/m，i=1,2,…,m，w1(i)表示第i个样本的权重，m表示当前训练集样本个数，D表示样本分布；

ifk>1 根据步骤5、6更新样本权重w1(i) endif

fort=1,2,…,Tkdo

2.根据样本分布Dt，从数据集St中构建训练集Rt和测试集Et；

3.调用CART算法，用训练集Rt训练得到决策树ct；

4.计算决策树ct在St=Rt+Et上的错误率εt：

ifεt>1/2删除该决策树，t=t-1, goto步骤2 else正规化错误率：βt=εt/(1-εt) endif

5.将所有决策树ct集成决策树Ccount：

计算Ccount在训练集Rt的错误率Et：

ifEt>1/2，删除Ccount，t=t-1，goto步骤2

6.标准化错误比值Bt=Et/(1-Et)，更新每个样本的权重wt+1(i)

endfor

使用多数加权集成所有决策树ct得到最终集成分类器Cfinal

I-CART算法由外层循环和内层循环组成，需要输入K个子数据集和迭代次数Tk. 子数据集的遍历在外层循环完成，生成具有差异性的基分类器在内层循环完成，此过程类似于Adaboost算法[14].

首先，初始化每个子数据集的样本权重，设置为1/m，m表示子数据集中有m个样本. 之后进入内层循环，执行步骤1，计算样本分布与样本权重，然后，针对样本分布Dt产生新的训练集. 样本权重决定训练集的构成，因为训练集由样本分布构造而成，而样本分布由样本权重产生. 再执行步骤3，将训练集输入CART决策树算法，训练得到基分类器ct，并将其加入集成分类器达到不断学习新数据的目的，充分体现了集成的思想.

为构造具有差异性的基分类器，提高集成分类器的泛化性，需要更新样本权重，得到不同的训练集，更新规则见步骤6.Bt为标准化的错误率，取值区间为(0,1)，由集成分类器Ccount(xi)得到正确分类的样本的权重与分布概率将会减小，其被选进训练集的概率会降低. 同理，被Ccount(xi)错误分类的样本的权重会增加，其被选进训练集的概率会增大. 这一点体现在步骤5和步骤6中，就是说，当有新类别出现时，现有的分类器会产生错误的分类结果，该分类错误的样本的权重就会增大，受到学习算法的特殊关注. 通过以上分析，由于I-CART算法不需要访问历史数据，对新数据学习的效率更具有优势.

步骤5、6也是使I-CART算法能够学习新类别的关键. 算法在迭代中通过增大分类错误样本的权重，增加其再次被选进训练集的概率，使得学习算法能够更多地关注被分类错误的样本. 因此，当有新的类别出现时，一定会被现有的分类器分类错误，成为分类错误的样本，该样本权重就会增大，使得学习算法关注这些具有新类别的样本，实现对新类别的学习. 从算法的执行来看，当有新数据加入时，应当返回到对子数据集的遍历即外层循环，首先需要执行的是每个子数据集的初始化部分，语句“ifk>1，根据步骤5、6更新样本权重和样本分布”会对新的数据样本进行评价，根据对新数据集的表现更新样本分布，增大分类错误样本的权重. 其中，具有新类别的样本一定包含在其中，这些样本被选进训练集中，实现了对新类别的学习，使算法具备了增量学习能力.

2 基于基分类器差异性与精确度关系的选择性集成算法

2.1 算法设计思路

在I-CART算法执行过程中，由于不断生成新的基分类器加入到集成分类器中，所以不可避免地会形成规模庞大的集成分类器，导致预测速率下降，影响预测性能. 选择性集成思想，就是不断剔除性能不好的基分类器，或者只挑选性能优异的基分类器来提高分类器性能[15]. 因此，本文借鉴了选择性集成的思想，解决集成分类器规模不断庞大的问题. 那么，如何选择基分类器成为选择性集成算法设计的首要问题.

实验证明：集成分类器中的基分类器分类精度越高、基分类器之间的差异越大时，集成效果越明显，两者缺一不可. 据此，本文首先对分类器间差异性与精确度的关系进行了探究，然后提出了一种基于差异性与精确度关系的选择性集成算法，并将此算法加入到I-CART算法中. 在I-CART算法外层循环执行完成后，即所有的基分类器训练完成后再进行此选择性集成算法，选择出更优的基分类器子集构成最终的集成分类器. 该算法提高了分类器正确率，显著减小了集成分类器的规模和存储压力，集成分类器的预测性能也得到提高.

2.2 基分类器差异性与精确度关系探究

Kappa系数是一种衡量分类精度的指标，将Kappa系数作为2个分类器的差异性度量准则时，其取值范围为κ≤1.κ=1时表示分类结果完全相同，不具有差异性；κ=0时表示分类结果相同，是偶然产生的，具有差异性；κ<0表示分类器分类结果具有很大差异性.κ值愈小，表征2个分类器的差异性愈大. Kappa系数由算法2计算得到.

算法2 2个基分类器间的Kappa系数

输入：h表示当前基分类器，hi(xi)表示hi对样本xi的分类，yi表示样本xi对应的真实分类

输出：Kappa系数κ

图1、2分别为在航班数据集和Ionosphere数据集上基分类器的κ与分类误差率e关系图.

从图1和图2可以看出，κ减小时，基分类器的e变大，分类精确度变低. 根据选择性集成原理，应当尽可能集成那些差异性大且精确度高的基分类器. 然而，通过实验发现基分类器的差异性与精确度成反比，当选择差异性大的基分类器时，其精确度极低；当选择精确度高的基分类器时，它们彼此又不具备差异性.

2.3 选择性集成算法

2) threshold阈值为所有Kappa系数的平均值. 通过设置平均值而不是某个固定阈值使其能更好地适应不同的情况.

3) 按升序排序Error数组，产生基分类器序号并保存到数组Index，确保精确率最高的基分类器得到优先选择.

4) 从第一个κ值小于threshold的序号位置开始选择，节省了选择时间设计，不需要再依次比较.

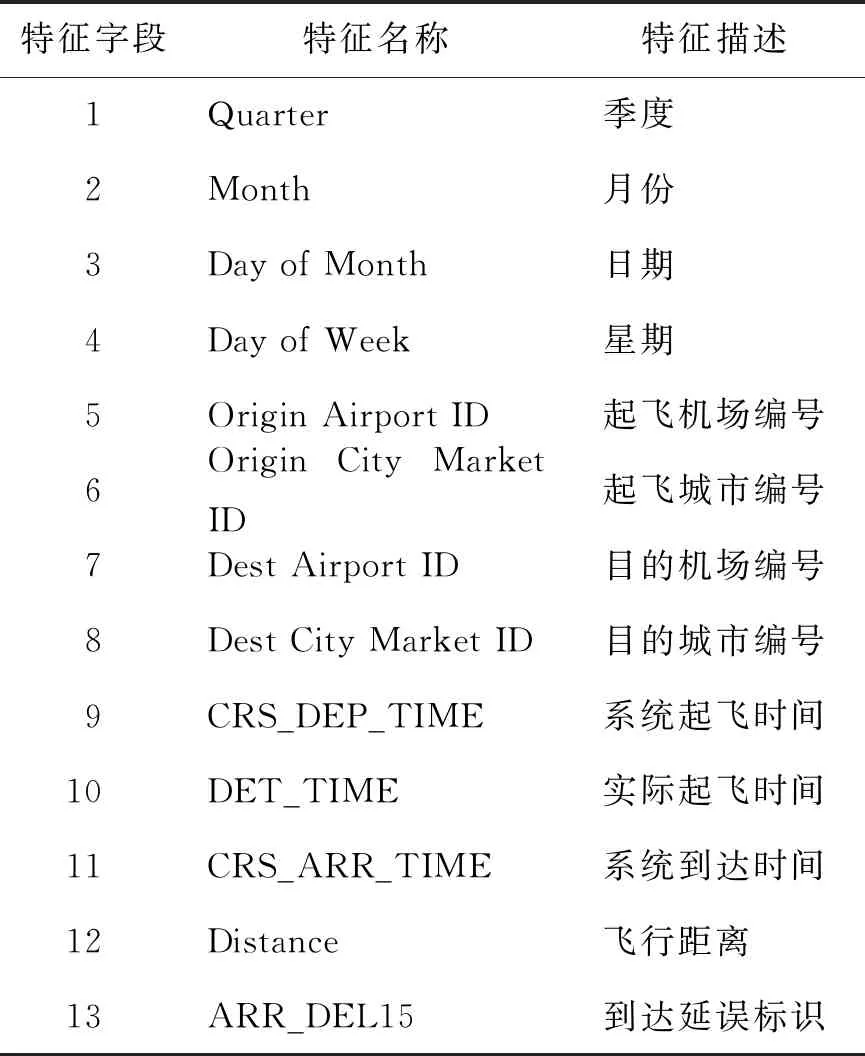
5) 从begin的位置开始选择基分类器，当κ

算法3 选择性集成算法

输入：指定选择基分类器的个数SN，开始选择位置begin；

输出：选择出最优基分类器

fori=1,2,…,N

ei=hi在测试集上的误差率

forj=i+1,2,…,N

ej=hj在测试集上的误差率

Error(m)=(ei+ej)/2,m∈[1,…,N2]

按照算法2计算hi与hj之间的κ

Kappa[m]=κ,m∈[1,…,N2]

endfor

2.设置阈值threshold=avg(Kappa)；

3.排序(升序)Kappa数组，并记录基分类器序号Index，SORT()表示排序函数

Index=SORT(Error)

4.设置开始选择性集成的位置

begin=INDEX(NO.1→Kappa(Index(i))

5.选择SN个基分类器hc,c=1,2,…,SN

hc表示选择出的基分类器，hIndex表示序号为Index的基分类器

whilec≤SNdo

if Kappa(Index(j))

hc=hIndex，c=c+1

3 实验设计与结果分析

3.1 实验数据集

本文利用美国交通运输统计局(Bureau of Transportation Statistics)网站的航班准点数据集(airline on-time performance data，AOTP)[16]，它包含了美国1987年至今的航班数据，并选择纽约2018年2月份与5月份产生的航班数据，共105 159条. 其中，删除了2 505个具有缺失值的样本后，将剩余的102 654个样本作为本文实验数据集. 对航班数据特征进行分析和数据特征选择后，本文选择了13个特征，其中，第1～12个特征为标识航班信息的重要属性，第13个为是否延误标志，准点到达目的地机场，其值为0，晚点到达15 min以上的，其值为1. 具体特征描述如表1所示.

表1 航班数据特征描述Table 1 Description of flight data characteristics

3.2 实验设计与结果分析

实验1的目标是将I-CART算法和CART算法的分类误差率进行统计，以验证I-CART集成式增量学习算法的分类性能. 实验2和实验3分别从增量次数与增量数量验证I-CART集成式增量学习算法能够高效地学习新到达的数据并具有良好的预测性能. 实验4用来验证分类器规模是否减少，预测效率是否能够提高.

3.2.1 实验1

I-CART算法参数见表2，设置I-CART算法参数，K表示子数据集个数，Tk表示迭代次数，根据样本数量将K设置为5、10、20，保证每个子数据集中样本个数相同. 表3是算法在不同样本数量时的分类误差率，性能提升率为分类误差率的差值，公式为

性能提升率= CART算法分类误差率-I-CART算法分类误差率

(1)

由表3可知，I-CART算法与CART算法相比，在相同的训练数据量下I-CART算法的误差率普遍低于CART算法. 当样本数量为10万时，能达到0.565%的性能提升，证明I-CART算法当面临海量数据训练时分类性能比单分类器CART算法更优.

表2 I-CART算法参数Table 2 Parameters of I-CART algorithm

表3 实验1分类误差率统计Table 3 Statistics of classification error rate in experiment 1

3.2.2 实验2

在该实验中，将5 000作为固定增量，即每次增加5 000个新样本；增量次数分别设置为第5、10、20次，即当新数据在第5次、第10次、第20次到来时，学习新数据更新时需要的时间. 表4为实验2在不同增量次数下的时间统计表，耗时比计算方式为

(2)

表4 实验2算法执行时间统计Table 4 Statistics of algorithms execution time in experiment 2

由表4可知，针对不同的增量次数， I-CART算法的执行时间分别是CART算法的49.63%、51.09%、46.48%，大大减少. 随着增量次数的增加，虽然2个算法的时间均有增多，但总体来看，I-CART算法学习新数据的时间还是大大缩短.

3.2.3 实验3

此实验从增量数量的角度验证I-CART算法能提高新数据的学习效率. 在该实验中，增量次数固定为10次，新数据每次以2 000、5 000、10 000个到达. 表5为时间统计表，耗时比计算方式见式(2).

表5 实验3算法执行时间统计Table 5 Statistics of algorithms execution timein experiment 3

由表5可以看出， I-CART算法执行时间分别是CART算法的53.95%、48.21%、49.57%，约是CART算法所需时间的49%，表明该算法大大缩短了学习新数据所需时间.

3.2.4 实验4

为证明本文提出算法的有效性，将选择性集成算法加入I-CART算法进行选择性集成. 设置I-CART算法子数据集个数K=30，迭代次数Tk=3，选择后基分类器的个数设置为SN1=20、SN2=30、SN3=45，如表6所示. 表7为最终集成分类器中对应个数的分类误差率，表8为对应的预测时间.

表6 实验4参数设置Table 6 Parameters settings in experiment 4

表7 实验4分类误差率统计Table 7 Statistics of classification error rate in experiment 4 %

表8 实验4预测时间统计Table 8 Statistics of prediction time in experiment 4 s

I-CART算法表示，当未执行选择性集成算法时，生成的集成分类器中包含90个基分类器；SN1、SN2、SN3表示当执行选择性集成算法时，原分类器规模减小为原规模的2/9、1/3、1/2. 可以看出，选择性集成算法在参数SN2时产生最好的分类效果，集成分类器规模减小为原来的1/3，节省了约67%的存储空间，预测速率提高约68%.