基于模格的密钥封装方案的比较分析与优化

王 洋 沈诗羽 赵运磊 王明强

1(山东大学数学学院 济南 250100) 2(复旦大学计算机科学技术学院 上海 200433) 3(密码技术与信息安全教育部重点实验室(山东大学) 济南 250100)

自从1976年Diffie和Hellman[1]提出利用单向陷门函数构造公钥密码算法以来，基于不同困难问题设计的各种各样的公钥密码体制相继被提出，并在密码学中有着极其广泛的应用.目前广泛使用的基于数论假设困难问题(如因子分解和离散对数问题)设计的公钥密码体制可以被Shor算法[2]在量子多项式时间内攻破.随着20多年来量子计算机技术的快速发展以及抗量子密码技术的研究，后量子密码算法的标准化工作也逐渐被提上日程.2016年美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)正式发起了对公钥加密(public key encryption, PKE)、密钥封装(key encapsulation mechanism, KEM)和数字签名这3类基本公钥密码算法相关的抗量子密码算法标准的征集工作.第1轮69个候选算法中有26个算法入选到第2轮评估[3]，这其中有12个候选算法(如NewHope,FrodoKEM,CRYSTALS-KYBER,SABER,LAC等)是基于格中困难问题设计的.CRYSTALS-KYBER和SABER更是入选为NIST最近公布的第3轮竞选算法[4].2019年我国举行了后量子密码算法竞赛[5-6]，获奖的算法也大多是基于格中的困难问题设计的，其中密钥封装算法包括：Aigis,LAC,AKCN-MLWE,Scloud,Tale等.

设计PKE和KEM时最常用的格中困难问题是(环,模)LWELWR问题[7-10].非正式地讲，标准形式(normal form)判定版本的(多项式)模LWE问题[11]是：给定模中均匀选择的矩阵A，以及某些向量b，判断b是中的均匀分布还是b=As+emodqR，其中s和e服从Rl上的某分布μ.而模LWR问题为给定模中均匀选择的矩阵A，以及某些向量b，判断b是中的均匀分布还是b=As，其中s服从Rl上的某分布μ.本文中我们采用系数嵌入来进行讨论.可以证明，对于适当的环R和分布μ，上述问题的困难性可以归约到一类格中worst-case的基本困难问题(如SIVPγ)上.模LWE问题的s和e服从Rl上的相同分布μ.为了进一步平衡安全性、实现效率以及通信带宽，文献[12-13]提出了非对称的LWE问题，即s和e服从Rl上的不同分布(更确切地说，是服从不同参数的某一类分布).目前，不使用复杂纠错码、接近于实用化的基于模LWELWR问题设计的高效KEM方案主要有2类：1)直接基于模LWELWR问题设计(如Kyber[14]，Saber[15]和Aigis[12])；2)基于文献[16-17]提出的密钥共识机制结合模LWELWR问题设计(如KCL[18],AKCN-MLWE,AKCN-MLWR和AKCN-Hybrid).上述2类KEM方案的构造方式均为先构造IND-CPA安全的PKE加密方案，然后采用Fujisaki-Okamoto(FO)[19-21]转换来构造满足IND-CCA安全的密钥封装方案.

共识机制是文献[16-17]提出的一种新的密码原语，由(Con,Rec)2个算法组成.非正式地讲，当输入均匀随机时，对称密钥共识机制的Con算法会输出某些相互独立的提示信号和随机的共识值.当Con和Rec算法的输入比较接近时，在提示信号的帮助下，Rec算法可以恢复出Con算法输出的共识值.非对称密钥共识机制则可以人为地决定共识值(即上述Con算法的共识值作为输入，输出的提示信号与输入的共识值彼此相互独立).文献[16-17]给出了一般性共识机制参数应满足的条件关系式，并设计了无条件安全的参数接近最优的非对称和对称的密钥共识机制.基于这些密钥共识机制，文献[16-17]依赖不同的困难问题设计了多种密钥封装方案，AKCN-MLWEMLWR和AKCN-Hybrid就是基于非对称密钥共识机制和模LWELWR问题设计的一种密钥封装机制.

本文的主要贡献有3个方面：

2) 由于Grove量子搜索算法的存在，为了实现大约256 b的量子安全强度，需考虑会话密钥长度约为512 b的KEM方案的设计.此外，目前的TLS1.3标准也强制要求提供512 b会话密钥的握手协商机制[22].因此，提供512 b的会话密钥也是现实的需求.对应Kyber-1024和Fire-Saber级别的参数,本文详细对比分析了3种可能的封装512 b密钥长度的方法.

3) 根据理论分析和大量实验测试，给出了AKCN-MLWE、AKCN-MLWR和AKCN-Hybrid的新的优化建议和参数推荐.同时也给出了对于Aigis和Kyber的优化方案(对应命名为AKCN-Aigis和AKCN-Kyber)和新的参数推荐.

1 相关工作

Kyber和Aigis采用的IND-CPA安全的PKE方案主要遵循文献[23]的设计框架(事实上目前很多基于LWE问题的PKE方案都是遵循这一框架设计的)，而后采用FO转换来设计满足特定安全性要求的密钥封装方案.文献[12]观察到了由于压缩技术的使用，模LWE问题的秘密s和误差扰动e对PKE方案最后的解密错误率的影响不对等，系统化地提出了非对称模LWE问题和模SIS问题，并从实际攻击的角度详细测试了不同参数条件下底层困难问题对应的安全强度.这使得Aigis可以更好地平衡安全性、实现效率、错误率和通信带宽的关系.Saber是直接基于模LWR问题设计的，采用的设计思路也是先设计IND-CPA安全的PKE方案，随后采用FO转换来设计密钥封装方案.AKCN-MLWE和AKCN-MLWR的设计采用了文献[16-17]提出的非对称的密钥共识机制.本质上讲，Kyber和Aigis采用的传统LWE形式的PKE方案以及Saber采用的模LWR形式的PKE方案均可以改写成非对称的密钥共识机制的形式(只不过采用的非对称的密钥共识算法与AKCN-MLWEMLWR的不同)，反之亦然.同时，我们注意到，结合原始AKCN-MLWE和Aigis的设计，我们可以更加优化参数的选择.需要说明的是，文献[23]及其变体密码体制均是针对加密单比特设计的.文献[16-17]中首先给出了更一般的加密形式并详细分析了相关参数所必须遵循的不等式界.

2 预备知识

本节定义一些符号并简单回顾Kyber,Saber,Aigis和AKCN采用的IND-CPA安全的加密体制的构造.

2.1 基本定义及符号说明

本文使用多项式环的系数嵌入并考虑分圆多项式环RZ[X](Xn+1)，这里n=2k为2的方幂.

在实际应用中，我们一般考虑秘密和误差服从中心二项分布的模LWELWR问题.对于正整数η，我们定义中心二项分布Sη为：取样U(({0,1}2)η)，输出环R上定义的判定版本模LWE问题为区分多项式数目的均匀样本与样本(ai,bi)，其中aiSη.判定版本的模LWE假设是说，没有概率多项式时间的量子敌手可以以不可忽略的优势解决判定版本的模LWE问题.而环R上定义的模LWR问题为区分多项式数目的均匀样本与样本(ai,bi)，其中ai对应地，模LWR假设是说，没有概率多项式时间的量子敌手可以以不可忽略的优势解决模LWR问题.

2.2 格密码体制常用的压缩函数

为了节省通信带宽，在实际应用中设计的密码体制一般会采用一些压缩技术.目前，在不使用额外纠错码的情况下，格密码体制最常用的压缩函数[12,14,24]为：

这里我们直接使用2d是为了充分利用存储空间.容易验证，对于x∈Zq，我们有:

为了讨论方便，我们称上述压缩函数为换模压缩函数.

在满足一定错误率要求的情况下，为了提高运算效率，文献[16-17]中也考虑了直接砍去低位比特的压缩函数：

此时，对于x∈Zq，我们容易计算得:

2.3 密钥共识机制

文献[16-17]中第1次提出一种称之为密钥共识的密码原语，利用此密码原语可以基于不同的困难问题设计密钥封装和公钥加密体制.AKCN-MLWE,AKCN-MLWR和AKCN-Hybrid就是采用非对称的密钥共识算法基于模LWE问题、模LWR问题和模LWELWR混合问题设计的IND-CPA安全的公钥加密方案，进而通过现有的通用构造来设计IND-CCA安全的密钥封装协议.

定义1.非对称密钥共识算法[16-17]AKC=(params,Con,Rec)的定义为：

2)V←Con(Σ2,K2,params).在输入为Σ2∈Zq,K2∈Zm和params的条件下，概率多项式时间算法Con输出公开提示信息V∈Zg.

3)K1←Rec(Σ1,V,params).在输入为Σ1∈Zq,V和params的条件下，确定多项式时间算法Rec输出K1∈Zm.

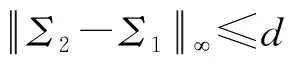
成立，这里概率取自Σ2U(Zq)和Con中使用的随机性.在后续的讨论中，为了方便会省略掉params.文献[16-17]证明了满足正确性和安全性的非对称密钥共识算法的参数params应满足的条件.

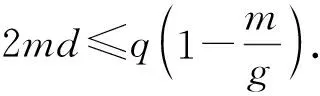
2.4 AKCN-MLWEMLWR加密算法

文献[16-17]基于非对称的密钥共识算法设计了IND-CPA安全的公钥加密体制AKCN-MLWE和AKCN-MLWR.具体构造分别如图1和图2所示(图2为参数为2的方幂情况下的简化版本).其中AKC=(Con,Rec)可以是任意满足正确性和安全性的非对称密钥共识算法，Gen为某特定的输出伪随机的扩展函数.

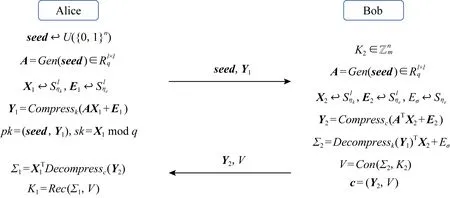
Fig. 1 IND-CPA secure encryption schemes used by AKCN-MLWE图1 AKCN-MLWE采用的IND-CPA安全的加密体制的构造

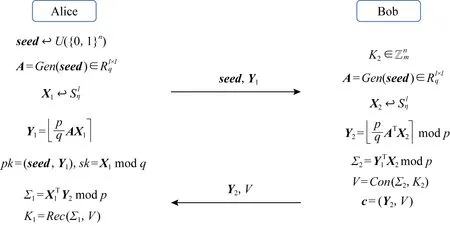
Fig. 2 IND-CPA secure encryption schemes used by AKCN-MLWR图2 AKCN-MLWR采用的IND-CPA安全的加密体制的构造

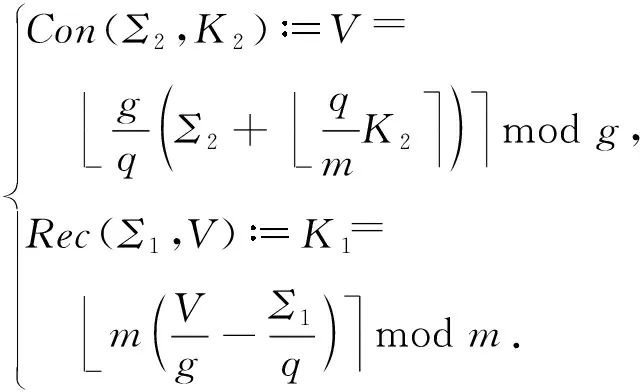
(1)

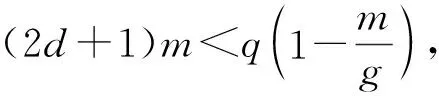
2.5 LWELWR加密算法

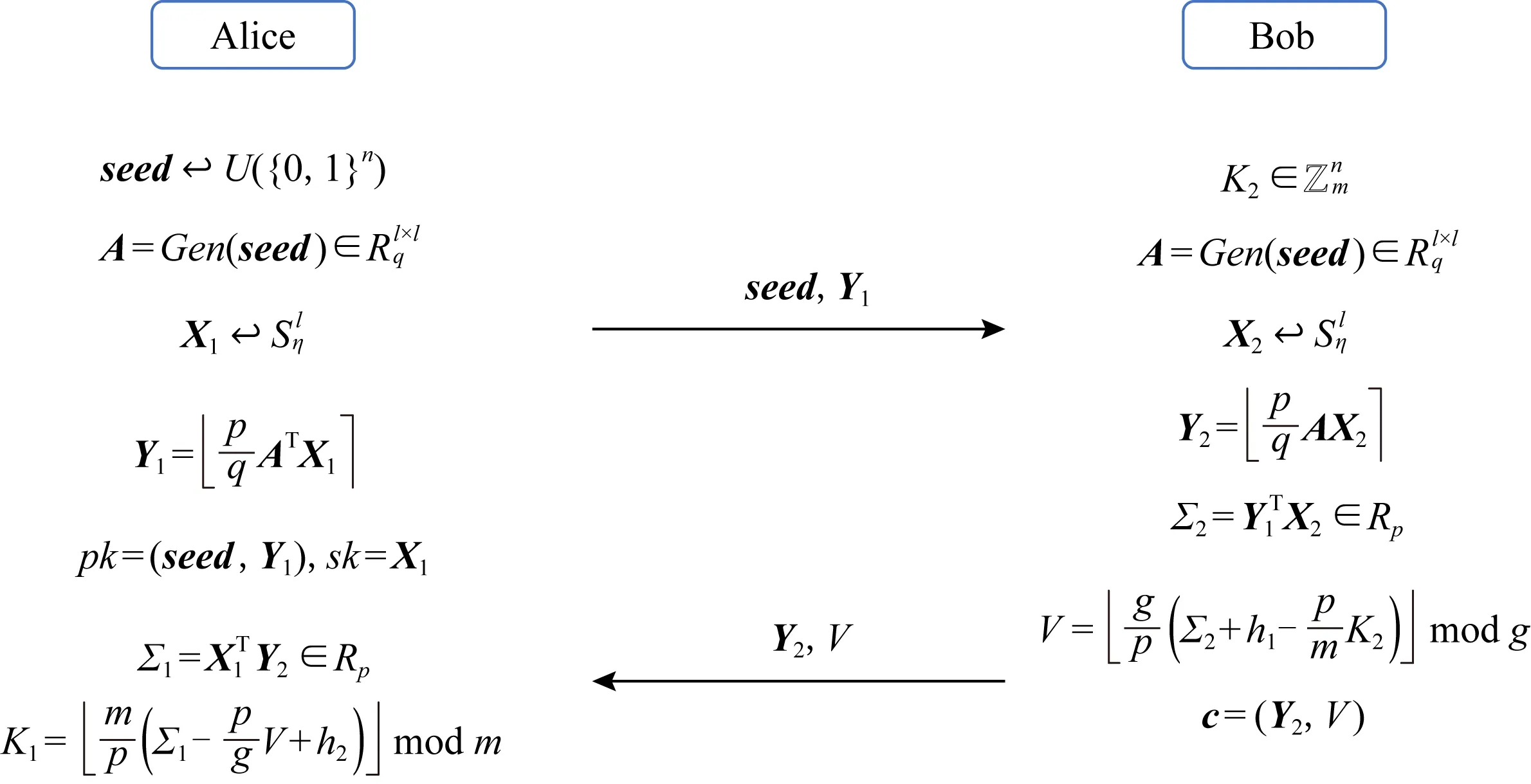
Fig. 4 IND-CPA secure encryption schemes used by Saber图4 Saber采用的IND-CPA安全的加密体制的构造

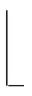
Saber选择的参数与AKCN-MLWR一样均为2的方幂.注意到对于这种参数选择，对任意的x∈Zq，我们有:

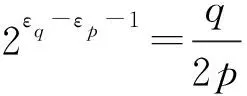
需要特别说明的是，基于非对称密钥共识机制的AKCN-MLWEMLWR的算法描述是对于一般性m的.而在Kyber和Saber方案的实际描述是针对特定m=2这种情况.实际上，针对多比特m>2的密钥共识机制和密钥封装机制最早在文献[16-17]中被明确提出，并详细给出了参数(q,m,g,d)之间必须遵循的不等式界.

3 共识机制形式下加密体制对比分析

3.1 LWE加密体制转换为共识机制加密体制

(2)

这里我们采用明文内嵌入.当g|q时，LWE形式的加密算法转换的非对称密钥共识算法与AKCN-MLWE采用的完全一致.但是对于一般的g和q，二者并不相同.使用类似文献[16-17]中的证明方法，我们可以得到如下引理.

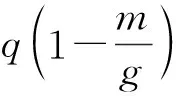
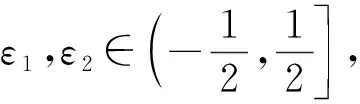
带入K1的表达式计算可得:

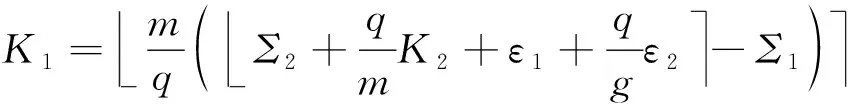
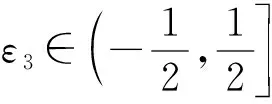
根据假设，存在θ′∈Z和δ∈[-d,d]使得Σ2=Σ1+θ′q+δ.所以，我们可以推出:

要满足正确性，则只需满足关系式:

证毕.

当统一成共识形式的加密体制时，可以看出AKCN-MLWE采用的共识算法要比Kyber等采用的LWE加密形式转换而来的共识算法要好一些.但是二者非常的接近.注意到图1中基于共识算法设计的加密体制的误差的取值均为整数，所以尽管从数学上看，AKCN-MLWE采用的非对称密钥共识机制要优于Kyber等采用的LWE加密形式转换而来的非对称密钥共识机制，但是对于某些参数来说，根据参数满足的关系式计算而来的d的上界的差别可能在1以内.这就使得这2种形式最后计算的错误率可能相同.

3.2 LWR加密体制转换为共识机制加密体制

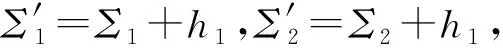
(3)

由于现在参数都是2的方幂，我们可以使用更简单的方法推出引理2.

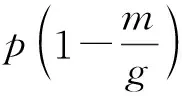
证明. 根据定义和参数选择，我们有:

其中,εV∈[0,2εp-εg-1]∩Z.所以，我们可以推出:

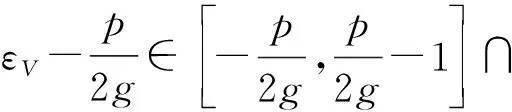
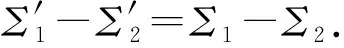
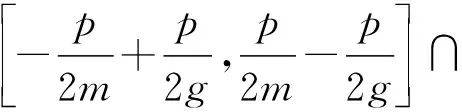
(4)

时，有K1=K2.这等价于

证毕.

需要指出的是，文献[16-17]在推导AKCN-MLWR对应参数条件下共识机制式(1)所满足的界时采用了一些近似(采用的推导方法与一般参数的推导方法类似).当使用类似引理2的证明方法来推导共识机制式(1)所满足的正确性条件时，可以得到当Σ1-Σ2的系数均落在区间

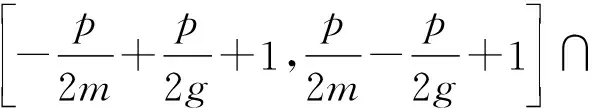
时，K1=K2成立.对比式(4)可知，当统一成共识机制形式的加密体制时，AKCN-MLWR与Saber采用的共识机制参数所满足的正确性条件相差很小.

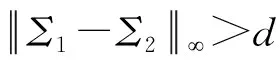
4 基于MLWE的KEM错误率比较分析

本节系统比较分析基于MLWE的密钥封装机制在不同压缩函数和加解密方式下的错误率差异.3.2节提到AKCN-MLWEMLWR如果直接利用AKCN的正确性条件分析得到错误率会比其实际的错误率略高，为了更精确地分析AKCN-MLWEMLWR的具体错误率，我们将其转换为传统LWELWR加密体制的形式然后进行错误率分析.事实上，这就是将AKCN采用的非对称密钥共识算法(Con,Rec)简单展开的过程.

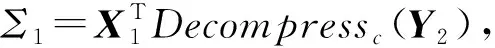
所以与Kyber以及Aigis等使用的传统的LWE形式的加密体制相比，AKCN-MLWE非对称密钥共识机制转换的LWE形式加密体制的解密算法相当于未对第2个密文V完全解封装，节省了1步四舍五入运算.特别地，实际测试表明，多加1步四舍五入运算不仅增加了计算量，也相当于增加了额外的误差，从而会造成错误率偏高.

则图3所示LWE形式加密体制的解密计算中，有:

其中，

Err=(E1-ε1)TX2-X1T(E2-ε2)+Eσ-εv

(5)

(6)

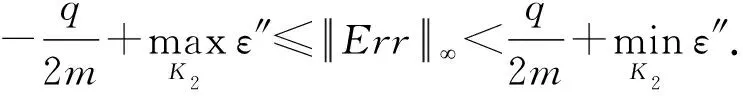
(7)

与式(6)相比，对于绝大部分参数(特别是m比较大时)，明文内嵌入的方式带来的错误率会更小.但是当m比较小时，这2种嵌入方式对应的错误率大小需要视具体参数的选择而定.

对于AKCN-MLWE对应的情况，我们采用上述符号并记:

则计算可得:

此时，采用明文外嵌入和明文内嵌入2种方式对应的错误率同样可以结合关系式(6)(7)通过程序计算给出.

采用Kyber提交的在NIST前2轮竞选中提交的推荐参数，我们测试的错误率结果如表1所示:

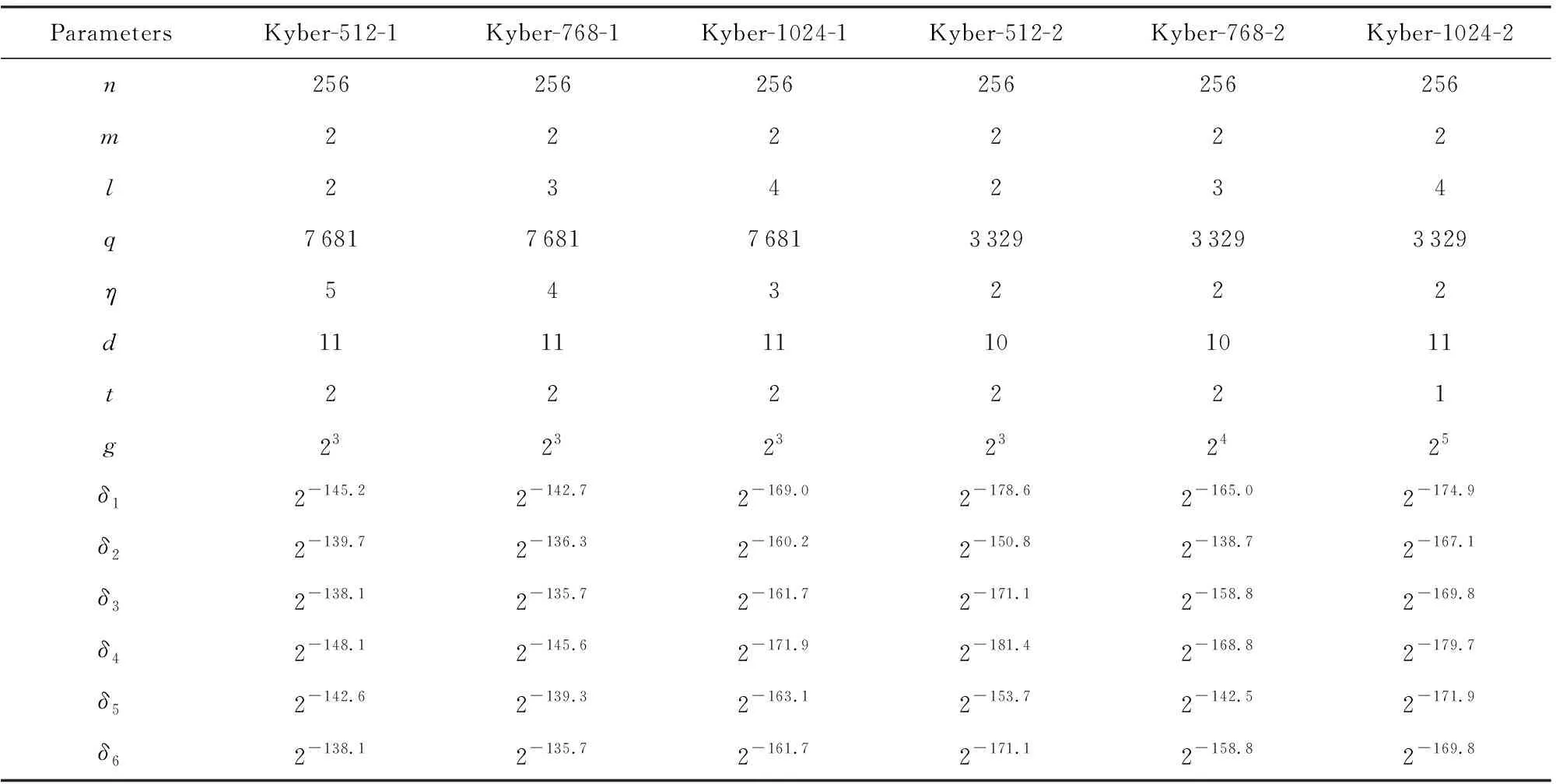
Table 1 Error Rates of Kyber Recommended Parameters表1 Kyber推荐参数的错误率

针对表1的测试数据，我们给出4方面的讨论.

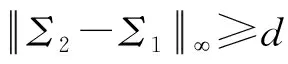
Σ2-Σ1=(E1-ε1)TX2-X1T(E2-ε2)+Eσ.

(8)

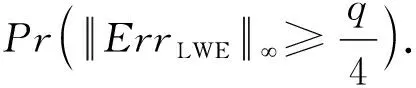
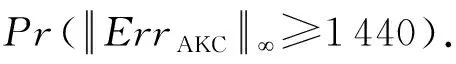
4) 对于固定的一组参数，当采用相同的压缩函数时，AKCN-MLWE使用的非对称密钥共识算法转换而来的LWE加密形式的密码体制的错误率更低(如对比δ1和δ4，或δ2和δ5).这说明正如本节一开始指出的，对第2个密文V不进行完全解封装不仅能节省1步四舍五入运算，还可以降低错误率.这也从一个侧面表明了确实如3.1节分析，AKCN-MLWE采用的非对称密钥共识机制更优(注意到我们并没有对Y1和Y2也进行类似的操作.这是因为我们需要利用Y1和Y2使用NTT算法来进行乘法运算.因此，需要将Y1和Y2解压缩为环Rl中的元素).

5 基于MLWR的KEM错误率比较分析

本节对AKCN-MLWR与Saber的错误率进行对比分析.此时，我们假设参数q=2εq，p=2εp，g=2εg和m=2εm满足条件εm≤εg<εp<εq.对比图2和图4可知，AKCN-LWR采用共识机制转换的加密和解密分别对应为

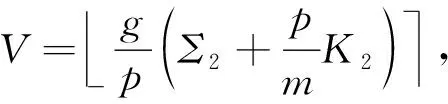
我们有:

其中,εV∈[0,2εp-εg-1]∩Z.因而，我们可以推出:

所以，正确解密条件为

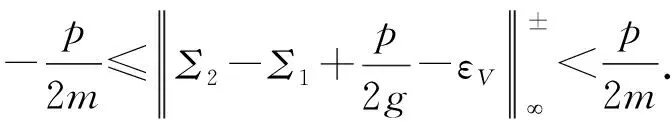
(9)

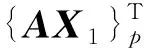
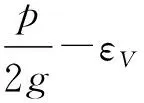
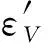
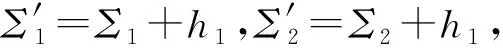
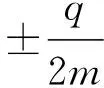
6 基于模LWELWR混合模式的KEM错误率分析

我们称文献[17]中使用非对称密钥共识机制同时结合模LWE和模LWR问题来设计CPA安全的加密体制的方法为AKCN-Hybrid，其具体构造如图5所示，其中的参数以及(Con,Rec)算法与第5节类似.

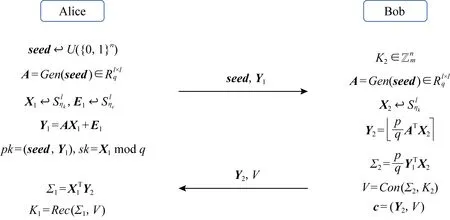
Fig. 5 IND-CPA secure encryption schemes based on Module LWELWR图5 同时基于模LWELWR问题设计的IND-CPA安全的加密体制的构造

此时，我们有:

记

则有

所以，当

时，可以正确解密.我们采用前面各节的符号，容易计算得到:

至此，我们可以利用类似第5节中AKCN-MLWR的假设或RLizard[25]的假设和处理方法使用程序来计算AKCN-Hybrid的错误率.

7 封装512 b的EKM方案对比分析

由于量子搜索算法(Grove算法)的存在，理论上来讲2λ比特长的密钥最多只能提供λ比特的安全强度.从这个角度来看，为了实现大约256 b的量子安全强度，我们需考虑会话密钥长度约512 b的KEM方案的设计.这对应着Kyber-1024和Fire-Saber这2组参数.此外，目前的TLS1.3标准也强制要求提供512 b会话密钥的握手协商机制[22]，因此提供512 b的会话密钥也是现实的需求.

根据前面的分析并为了简化讨论，在本文后续部分讨论错误率时，我们仅使用换模压缩函数和基于AKCN共识机制的加解密函数(这是由于我们在本节中需要明确地考虑加密多比特的情况)但采用将AKCN共识机制展开成LWE加密形式进行更为精确的错误率分析.LWR形式对应的分析是类似的.首先，如Aigis观察到的，由于压缩函数的使用，LWE误差Ei和秘密Xi对于最后解密误差Err的影响不对等.特别地，当固定q，dk，dt和g时，改变ηk对Err带来的影响要比改变ηe带来的影响大得多.此外，互换dk和dt的值对最后的解密误差几乎无影响.这是因为对于一般的参数，误差(E1-ε1)TX2-X1T(E2-ε2)服从的分布与误差-(E1-ε1)TX2+X1T(E2-ε2)服从的分布几乎相同.当公钥和第一个密文的压缩尺寸不同时，我们一般采取公钥压缩的比特数目较少(即公钥压缩后的规模大)，第1个密文压缩的比特数目较多来与Kyber NIST Round 2的设计保持相近.

为了达到封装512 b会话密钥且不低于200 b后量子安全的目的，基于MLWE问题，我们主要有3种实现方法:1)采用Kyber NIST 第2轮1024参数进行2次封装，即n=256，l=4，m=2封装2次；2)采用类似的参数，考虑m=4封装1次；3)扩大环的扩张次数，即设置n=512，l=2，m=2封装1次.

我们首先来比较前2种方法，使用方法1的设置来共享512 b会话密钥相当于要用同一个公钥来进行2次封装，此时错误率至多为原来2倍，总通信带宽为

n+nldk+2(nldc+nlbg).

使用方法2的设置来共享512 b会话密钥只需封装1次，但是我们要考虑错误率.共识加密形式下参数应满足的关系式(如引理1)为我们计算错误率提供了启发式的参考.在误差分布变化不大的情况下，当m增加1倍时，我们只需要把q和g均增加1倍即可保证错误率变化不大.理想情况下，采用方法2的设置的总通信带宽约为n+nl(dk+1)+nl(dc+1)+n(lbg+1).所以，前2种方法的总通信带宽的差为

Δ=nl(dc-2)+n(lbg-1).

由于实用中，dc和g均不会太小，所以方法1的总通信带宽一定比方法2大.在实用中我们一般选择q为满足NTT计算条件的素数，且当q增大1倍左右，g,dk和dc增加1 b时，误差项中的εv，ε1和ε2均会发生变化，改变的大小与q有关，所以实际应用中不像理想情况分析的那样.但是我们仍可以按照上述分析来大致确定参数再通过具体程序测试来微调确定哪一组参数较优.

我们对比测试NIST第2轮的Kyber-1024这一组参数，结果如表2所示:

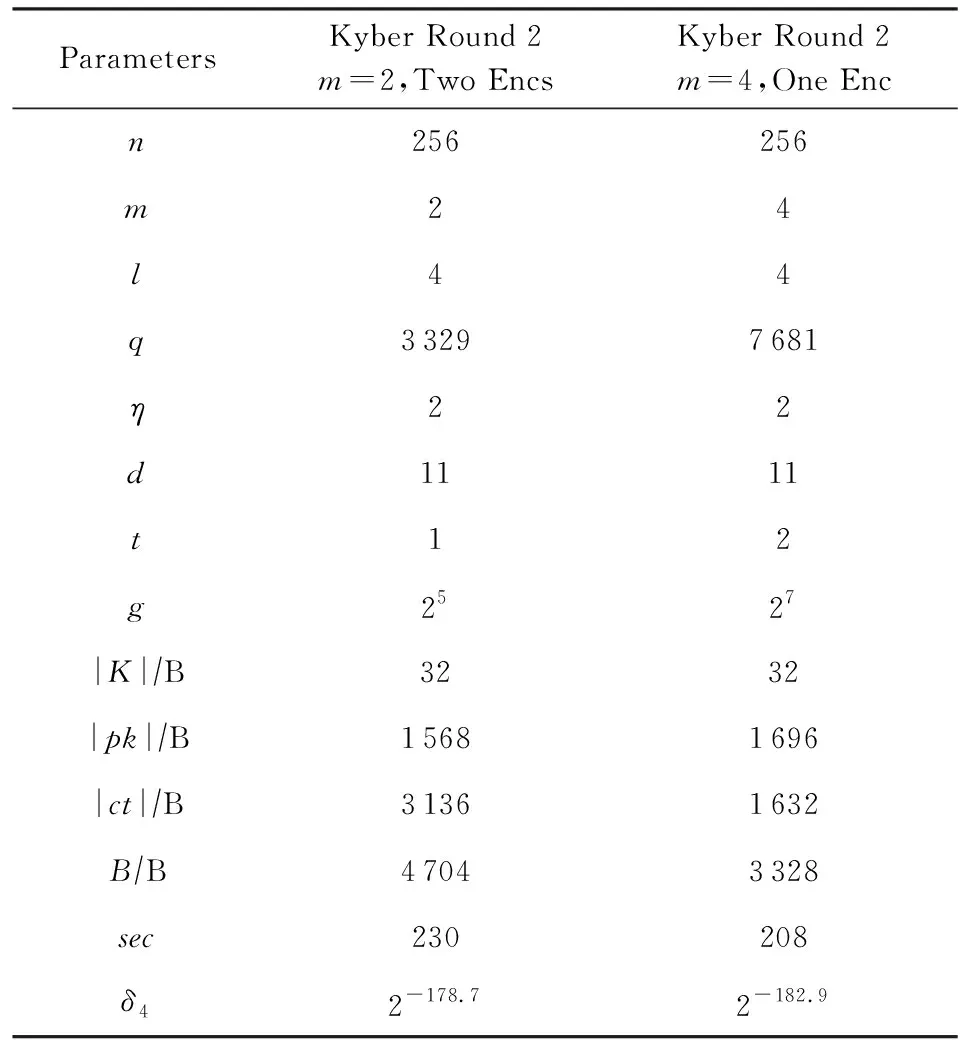
Table 2 Multi-bits Comparisons of Kyber Round 2表2 Kyber第2轮参数多比特测试比较

表2的符号与表1一致，不同的是，|K|,|pk|,|ct|和B分别表示共享密钥长度、Alice和Bob各自传输信息的带宽以及总通信带宽，单位为B；sec表示对应参数的密码体制的量子安全强度.

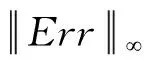
综上所述，对于绝大多数的参数设置而言，方法3采用的设置可以更好地平衡错误率、安全强度与通信带宽.但对应的缺点是：在具体实现时需要修改一些算法，在算法兼容性和适配性上不如方法2.

8 优化的KEM方案和参数推荐

根据本文针对基于模格的KEM方案系统性的比较分析，在本节中我们给出基于模格KEM的方案优化，并通过大量的测试给出新的参数推荐.

针对基于MLWE的KEM方案，在相同的参数选择下，本文的比较分析得出如下结论：同时采用基于AKCN-MLWE共识机制的加解密过程和换模压缩函数是更优的组合.首先，基于AKCN-MLWE共识机制的加解密过程更为简单高效，同时本文的具体错误率分析方法(即错误率不采用AKCN-MLWE原始共识机制的正确性条件进行粗略计算，而是进行更为精确的具体分析)也表明基于AKCN-MLWE共识机制的加解密算法具有更低的错误率.其次，虽然换模压缩函数相对于砍比特压缩函数要复杂，但是对应的会带来更低的错误率，同时也可以更好地与Kyber和Aigis进行兼容.

相对于原始的AKCN-MLWE，本节优化的AKCN-MLWE方案仅更换了其压缩函数；相对于Kyber和Aigis，本节优化的AKCN-MLWE可以视作仅对其解密算法做了优化(更简单且错误率更低)，而密钥生成和加密算法仍然和原始的Kyber和Aigis方案保持一样.这样，优化后的AKCN-MLWE方案可以取得与Kyber和Aigis方案最大程度的兼容和适配.在后文的描述中，AKCN-MLWE方案默认是这种优化的方案.另外，和Kyber的NIST第2轮提案一样，从保证可证明安全性的角度，我们也默认AKCN-MLWE不对公钥的Y1进行压缩.但是Aigis采用的是类似Kyber在NIST第1轮中采用的2轮压缩的构造方式，所以表5中为保持一致，AKCN-Aigis同样也采用2轮压缩的构造方式.

为了表述方便，后文我们记AKCN-Kyber为将NIST第2轮的Kyber加密方案的解密过程换成AKCN-MLWE共识形式转换的解密形式；同样地，AKCN-Aigis表示将Aigis加密方案的解密过程换成AKCN-MLWE共识形式转换的解密形式.

AKCN-MLWE与AKCN-MLWR的新参数推荐如表3和表4所示，采用的符号与表1和表2相同.对于AKCN-MLWE-1024这组参数，目标是封装512 b的密钥，我们分别给出了2种方式下的具体参数：AKCN-MLWE-1024-1是n=256和m=4，从而具有更好的兼容和适配性；AKCN-MLWE-1024-2采用n=512和m=2，具有更优良的带宽性能.

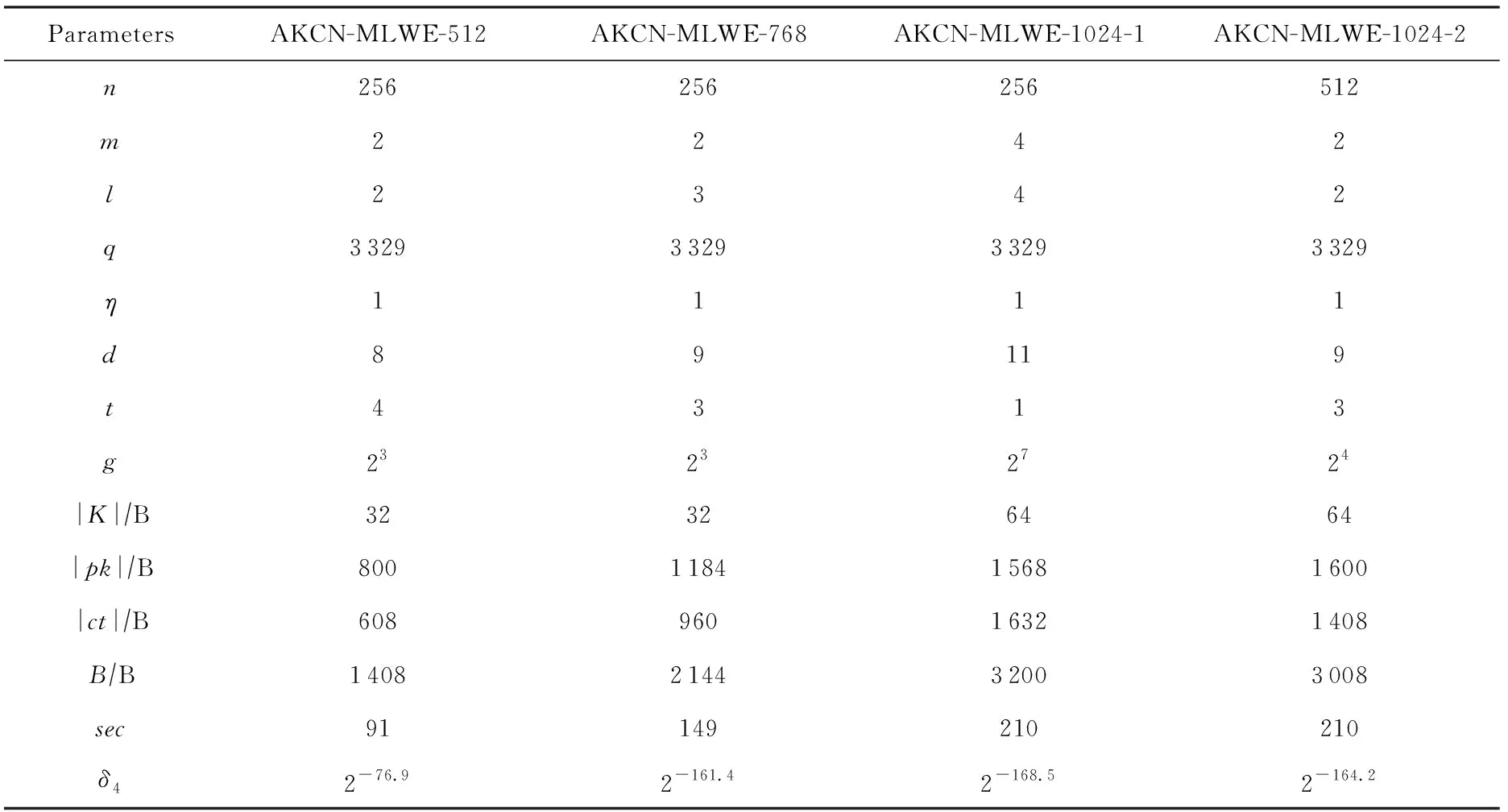
Table 3 New Parameters of AKCN-MLWE表3 AKCN-MLWE 新参数

Table 4 New Parameters of AKCN-MLWR表4 AKCN-MLWR 新参数

Continued (Table 4)

在表4～7中，δ表示错误率.由于我们想要使用相同的参数q，当q=212时很难像AKCN-MLWE-1024-1一样同时兼顾安全性与错误率，因此AKCN-MLWR-1024-1仍然是封装256 b的密钥.注意到，由3.2节和第5节的分析，AKCN-MLWR的新参数也可以看作是对Saber NIST Round 2的3组参数的优化推荐.

我们给出的AKCN-Aigis的新参数推荐如表5所示.表5中采用的符号同样与表1和表2相同.为了便于比较，我们也将Aigis的参数列出来.其中，Aigis-512,Aigis-768和Aigis-1024分别对应文献[12]中加密体制推荐参数Params I,Params II和Params III.与Aigis推荐的参数相比，AKCN-AIGIS采用了统一的q=7 681(Aigis-1024采用的是12 289)和统一的中心二项分布参数(ηk,ηe)=(1,4)，这更有利于算法的模块化部署实现和增强算法的适配性.

由于Aigis-768推荐参数很好地综合了安全性和错误率，所以我们推荐的AKCN-Aigis-768的参数与Aigis-768相同.不同之处在于，AKCN-Aigis采用的解密算法相比于Aigis的更简单，同时在相同的参数下AKCN-Aigis的解密错误率也更低.值得指出的是，推荐参数AKCN-Aigis-1024-2可以与Aigis-1024在相近的安全强度下(208对比213)，能够以更低的错误率(2-216.2对比2-211.8)和更小的通信带宽(2 816 B对比3 008 B，节省了192 B，约6.3%的通信带宽)封装相同长度的密钥(512 b).

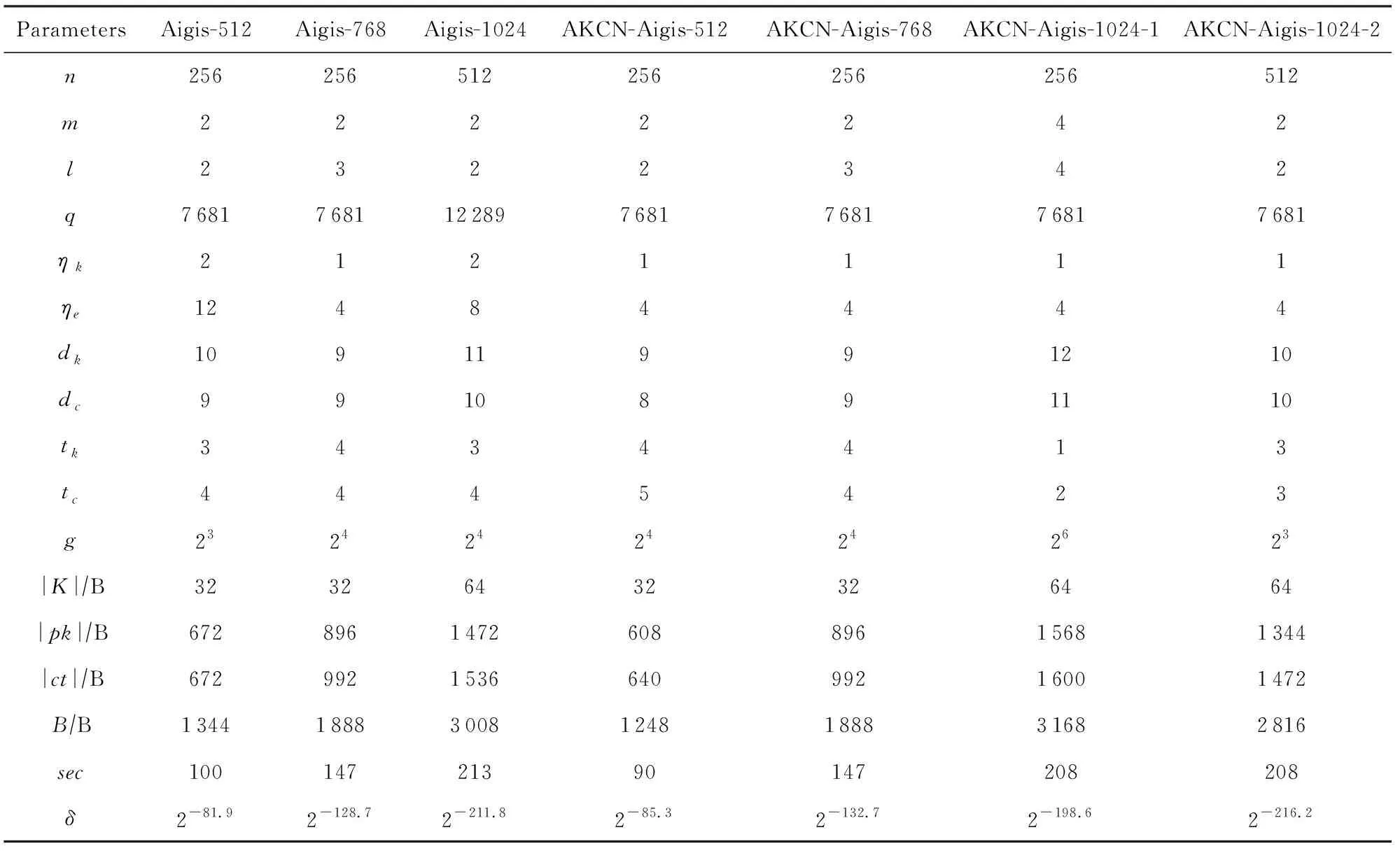
Table 5 New Parameters of AKCN-Aigis表5 AKCN-Aigis 新参数

我们在表6中给出AKCN-Kyber的新参数推荐.本节开头所述，AKCN-Kyber算法仅优化了Kyber的解密算法，使得解密算法更高效且错误率更低.为了和Kyber兼容，AKCN-Kyber-512768采用了Kyber-512768相同的参数，区别是错误率更低一些且解密算法更高效.AKCN-Kyber-1024是封装512 b的共享密钥，而Kyber-1024封装的是256 b的密钥.

最后，我们在表7中给出AKCN-Hybrid的新参数对比与推荐.其中，sec表示AKCN-Hybrid构造中依赖模LWE和模LWR问题设计的组件(长期私钥与临时私钥)对应的安全强度.

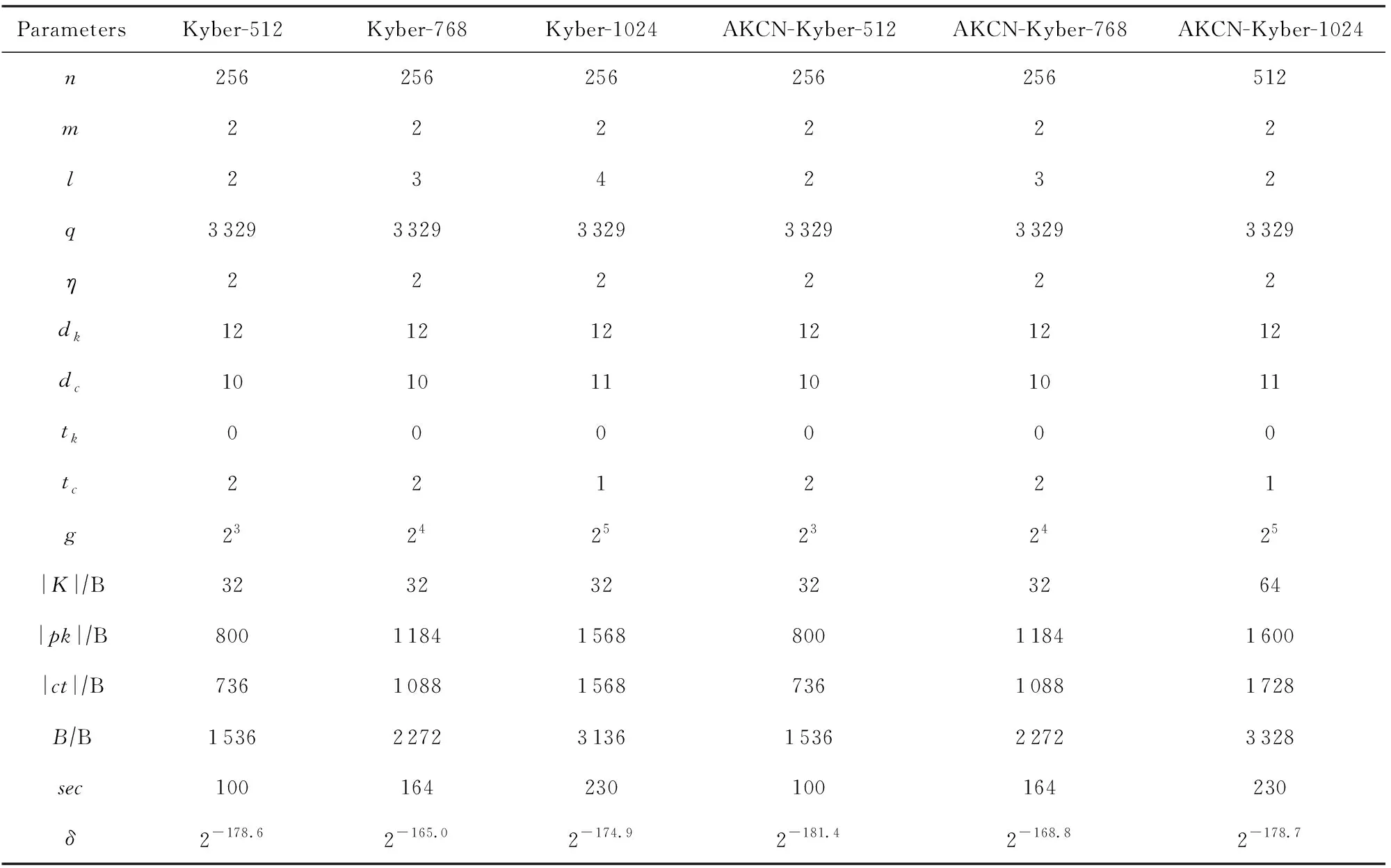
Table 6 New Parameters of AKCN-Kyber表6 AKCN-Kyber新参数

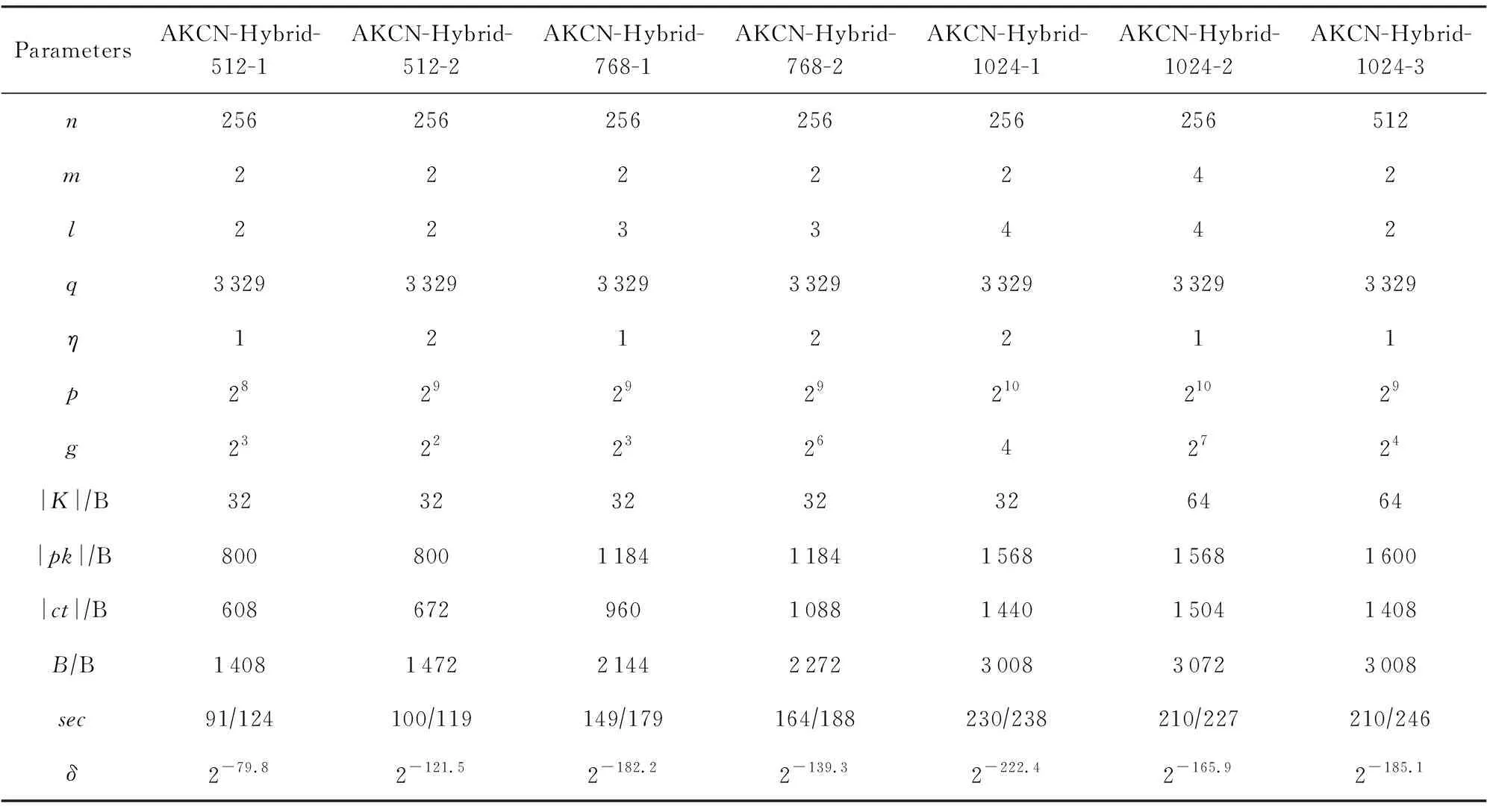
Table 7 New Parameters of AKCN-Hybrid表7 AKCN-Hybrid新参数

9 总 结