从探索中寻规律 在领悟中谋方法

吴伟莲

【摘要】新课标指出：有效的数学教学活动不能单纯地依赖模仿和记忆，“动手探索”是学生学习数学的一种重要方式，不断形成解决数学问题的策略，有效培养学生实践能力与创新精神.本文就如何引导学生在“动手探索”中寻找问题的解题规律，在“动脑领悟”中掌握数学的学习方法，逐步培养初中学生的“化归意识”与“化归思想”的主要方法和途径等来谈谈自己的一些见解和具体做法。

【关键词】 例谈;几何教学;化归思想

【中图分类号】G633.6【文献标识码】A【文章编号】1992-7711（2020）30-060-02

一、初中几何教学中“化归思想”的内涵及意义

“数学化归思想”就是把数学中待解决或未解决的几何问题，采用恰当的方法进行变换、转化，变成已经解决或比较易解决的问题，从而最终能够解决原问题的一种数学解题思想.在通常情况下表现在：未知与已知之间的转化;复杂问题与简单问题之间的转化;命题之间的转化;数与形之间的转化;空间与平面的转化;高次向低次的转化;多元向一元的转化;无限向有限的转化等等。

在初中几何教学中，应当结合具体的教学内容，让学生动手探索解题的途径与方法，渗透数学“化归思想”，老师不断培养学生用这种“数学思想”来解决数学问题，从而让学生体会和明白：初中几何的学习与解题的规律性，是有“法”可依的。

二、初中几何教学中“化归思想”培养的主要手段

让学生“动手探索”是培养化归思想的主要手段。有的数学教学活动不能单纯地依赖模仿与记忆，.新课标下的教材非常重视学生的活动，尤其对学生的探索能力的培养。新教材七年级已把实践探索纳入其中，例如：利用“粉笔盒”，让学生亲自动手探索图形在“展开与折叠”过程中是怎样变化的？让学生去发现结果的来龙去脉和可靠性，预留学生活动的时间和探索的空间。

三、初中几何教学中“化归思想”培养的主要方法

（一）从“作适当的辅助线”的方法——培养学生“横向化归”的思想

添辅助线的“化归思想”就是在对问题作细致观察的基础上，通过添加辅助线来展开联想，以唤起对有关知识的回忆，开启思维的大门，通过旧知识、旧经验来处理新问题.“横向化归”就是通过对命题的有关量进行转换，进行等价变换，通过同构变换等各种手段将很生疏、较复杂、比较困难的几何问题化归为我们最熟悉、较简单、很容易的数学问题来解决。;;

例1： 探究“多边形的内角和公式”

知识基础：学生已经学过三角形的内角和

教学基本思路：把几何中多边形问题全部“化”为三边形问题来解决。

设计问题：

问题1 ： 已学过的熟悉“正方形”、“长方形”的内角和是多少？学生答： 360° .

问题2： 四边形的内角和也是360° 吗？怎样得到的，你能找到几种方法？

问题3 ：通过“添加辅助线”而得到四边形内角和，类似可求五边形的内角和吗？n边形的内角和呢？

探究：学生动手操作，分组讨论、交流，探究方法，并共同进行归纳总结.学生中寻觅出了下列几种化归的方法（添辅助线）：

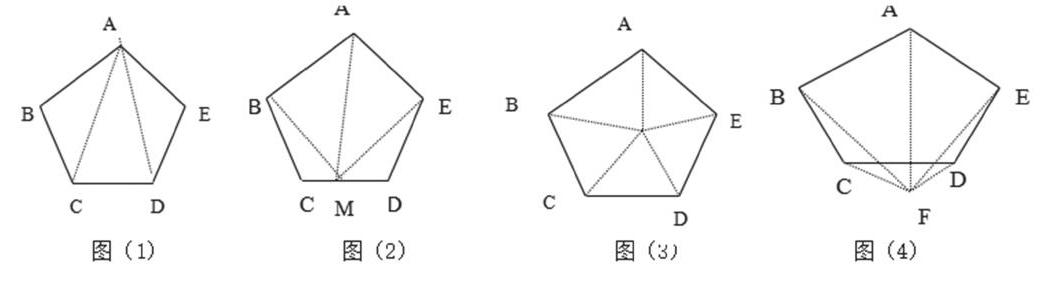
法1：如图（1）连结AD、AC，五邊形的内角和为：3×180°=540°;

法2：如图（2）在CD 上任取一点M，连接AM、BM、EM，求得五边形的内和为： 4×180°-180°=540°;

解题思路的共同点：是通过图形分割，把五边形问题化归为熟悉的三角形问题来解决.再选择当中的一种化归的路径，全部可以求出六边形、七边形等多边形的内角和，从而推导出任意n边形的内角和公式：180°（n-2）  （n≥3， n为整数）。

（二）  从“立体”到“平面”的方法——培养学生“纵向化归”的思想

“纵向化归”思想就是把学生碰到的几何新问题，通过“维降”等手段化为简单、熟悉的数学问题来解决.类似很多问题在长方体、圆柱体、圆锥体的侧面展开图中有较为广泛的应用.其基本的解题（化归）思想是：立体问题平面化。

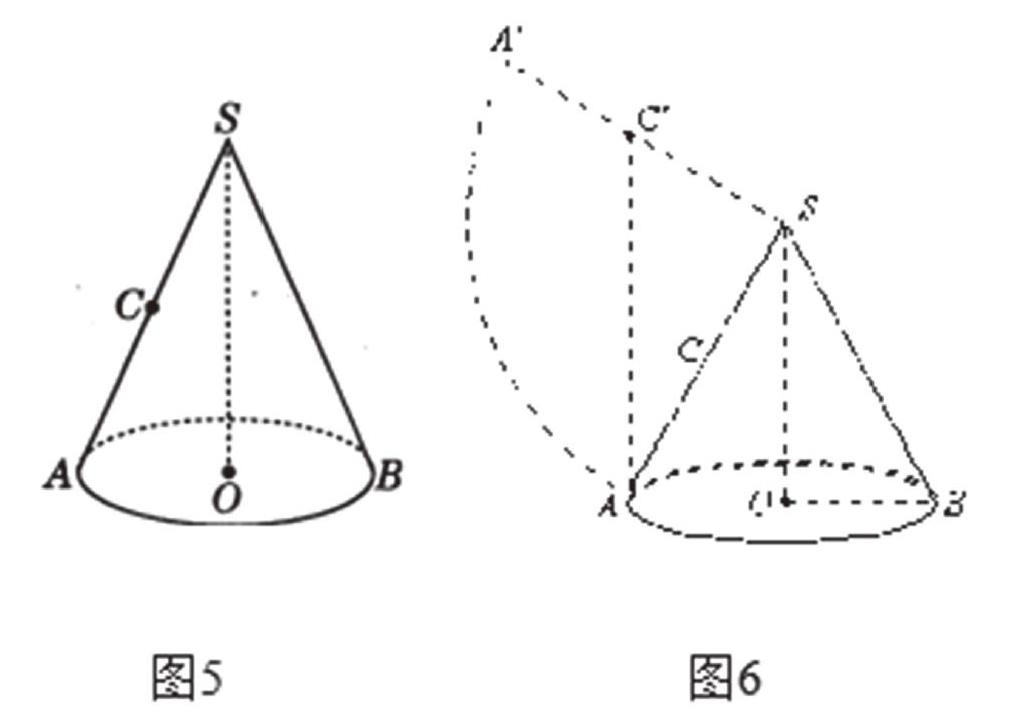
例2：  如图5，有一座山，大致呈圆锥，山底呈圆形，且半径OB为6千米，山高OS为415 千米.在山坡SA 的中点C有一联络站，要从山底A修一条盘山路，绕着山坡转一周将物资运到山坡AS的中点C，这条公路的最短路程为多少？;;;;;;;

对这个问题学生感到难以下手，可以要求学生制作简单模型，观察实验，可引导学生画出图形，就能把这个问题转化为在图6 中求线段AC′的长。

（三）从“特殊”到“一般”的方法——培养学生的“同向化归”的思想

“同向化归”就是对新面临的问题进行命题分割或分解，化为某个可简捷处理的子问题来进行处理，而这种“化归”在同一层次上是“平行”进行的。

例3 ：  自主探究《圆心角、弧 和 弦三者之间的关系》？

设计问题：

（1）圆是中心对称图形吗？它的对称中心是什么？

（2）什么叫圆心角？什么叫弦心距？

（3）学生事先准备好的两个等圆形纸片，并在两个等圆中分别画出两个相等的圆心角。

问题探究：在⊙O中，当圆心角∠AOB=∠A'OB'时，它们所对的弧AB和A'B'，弦AB和A'B'，弦心距OM和O'M'是否也相等呢？ （动手制作，实验探究，总结定理。）

（4）由探究得到的定理及结论是什么？（三个定理）

定理一：在同圆或等圆中，相等圆心角所对弧  相等 ;，所对弦 也相等  。

定理二：略（学生自己归纳完成）

定理三：略（学生自己归纳完成）

（5）在圆心角定理中，为什么强调“同圆或等圆”？可不可以删掉？

设计意图：调动学生学习的积极性，改变教师“填鸭式”教法，培养学生数学思维能力，在“实验与化归”中得到很好锻炼，数学知识技能也在潜移默化中得到很大提高，从而掌握了行之有效的学习方法。

（四） 从“用反证法”或“画反例图”的方法——培养学生“逆向化归”的思想

“逆向化归”思想是在解决数学问题时，出现较难入手，就按照习惯，如反证、举反例等采取正难则反的措施的数学思想。

例4：  求证：过在同一条直线上三点不可以作出一个圆。

可引导反设：设过A、B、C 三点能作⊙Q ;;;;;;;;;;

设计问题：（教师提问，学生思考回答：）

问题1 ： 点Q 到A、B、C 三点的距离有什么关系？

问题2 ： 作线段AB、BC 的垂直平分线L1、L2，则L1、L2 的交点在何处？

解题思路：引导学生自己画图，因为三个点都在同一直线上，学生极易想到：过点Q有两条直线垂直于同一直线，却与所学的“垂线公理”相矛盾，从而假设不成立，而原命题成立.当然，通常为了说明命题不成立，还可以举一个反例或画反例图来加以说明。

设计意图：既训练学生“逆向化归”思想，又为几何的证明开辟了新方法.事实证明，学习任何数学知识的最佳途径：是让学生大胆发现问题，解决问题。

【结束语】

加强几何“化归思想”的教与学，对于学生落实双基，培养学生的解题能力，锻炼学生思维，培养数学素养具有非常重要的作用，同时，也是学生形成几何认知结构的重要纽带，对数学知识转化为数学能力起到很好的桥梁作用。

【参考文献】

[1]罗增儒，数学思想方法的教学[J].中学数学教研，2015.

[2]郭立昌，浅谈加强数学思想方法教学的途径[J].数学通报，2016.

[3]沈文选，进行数学思想方法教学应注意的问题[J].中学数学，2017.