考虑后悔规避与匹配意愿的直觉模糊双边匹配方法
2020-11-10戴红军刘晓瑞
张 笛,戴红军,刘晓瑞
(1.南京信息工程大学 商学院, 江苏 南京210044; 2.淮南师范学院 经济与管理学院,安徽 淮南 232038; 3.南京航空航天大学 经济与管理学院,江苏 南京 211106)
0 引言
双边匹配是指对两互不相交集合中不可分的离散资源进行配对或分配问题,具有广泛的应用背景。现实生活中双边匹配问题普遍存在,例如:婚姻市场中的男女婚姻匹配问题[1]、人才市场中的人岗匹配问题[2]、金融市场中的风险投资匹配问题[3]、商品市场中的供需交易匹配问题[4]以及服务市场中的知识服务匹配问题[5,6]等。因此,研究双边匹配问题具有重要的理论意义和实际应用价值。
基于偏好序的双边匹配方法及其拓展研究一直是学者们的关注重点,众多学者从匹配的稳定性、满意性、抗操纵性和帕累托有效性等视角开展研究。概括起来,这些研究主要包括两个方面,一方面研究是建立在期望效用理论基础上的,即假设匹配主体的行为是完全理性的,并且这方面的研究已取得丰硕的成果[1,2,7~11]。在稳定匹配算法研究上[1,2,7]:Dogan等[1]、Azevedo等[2]以及Diebold等[9]学者在一对一稳定匹配的Gale-Shapley算法的基础上进行了一系列的拓展研究,并将双边匹配理论引入市场机制设计实践;为解决稳定匹配算法单边最优解的缺陷问题:樊治平等[8]提出一种考虑稳定匹配条件的双边满意匹配方法;梁海明等[19]构建基于认可差异和认可容忍的满意稳定、满意弱稳定和满意强稳定的匹配优化模型。在匹配的抗操纵性和帕累托有效性研究上:姜艳萍等[10]提出一种抗操作和抗自亏的双边匹配方法;Erdil等[11]研究了无差异偏好序下双边匹配的帕累托有效性问题。另一方面研究是考虑匹配主体的行为是有限理性的,大量实验研究表明,在双边匹配中,匹配主体并非总是追求效用最大化,而表现出参照依赖、损失规避和失望规避等心理行为特征,这方面研究主要是基于前景理论和失望理论等。目前,可以看到相关研究成果[12~15]:针对具有主体期望的双边匹配问题,乐琦等[12,13]分别提出基于累积前景理论的双边匹配方法、基于TODIM的双边匹配方法;李铭洋等[14]考虑匹配主体失望规避心理行为的双边匹配问题,构建基于失望理论的匹配优化模型;Fan等[15]将文献[14]的方法拓展至不确定偏好序情形。
已有研究丰富、发展和完善了双边匹配理论,然而,由于匹配环境的不确定性和人类思维的模糊性,在实际匹配中,匹配主体会给出模糊偏好信息。近年来,直觉模糊偏好信息下的双边匹配问题,引起了学者们的关注[16~19]:林杨等[16]提出一种兼具稳定性和满意性的双边匹配方法;乐琦[17,18]针对考虑匹配意愿的双边匹配问题,构建基于直觉模糊得分函数的匹配优化模型;Yue等[19]将文献[17,18]的方法拓展至区间直觉模糊偏好情形。上述文献为解决直觉模糊偏好信息下的双边匹配问题提供了思路和方法支撑。在双边匹配中,匹配主体的心理感知是不可忽视的重要因素,后悔理论[20]表明匹配主体不仅关注当前的匹配结果,而且关注如果选择其他匹配主体可能获得的匹配结果,并且尽量避免选择会使其感到后悔的匹配主体,即匹配主体是后悔规避的。需要指出的是,1)考虑匹配主体后悔规避心理行为的直觉模糊双边匹配方法的研究尚未报道; 2)双边主体的匹配意愿与匹配结果的满意程度密切相关[14],以往这方面的研究很少被关注。鉴于此,本文针对直觉模糊偏好信息的双边匹配问题,提出一种考虑匹配主体后悔规避心理行为和匹配意愿的双边匹配方法。
1 预备知识和问题描述
1.1 预备知识
首先给出本文需要使用的基础知识。
定义1[21]设H是给定的论域,称A={
定义2[21]设ρ1=<μ1,v1>,ρ2=<μ2,v2>是两直觉模糊数,则设ρ1和设ρ2的距离测度为
在双边匹配问题中,设X方主体集为X={X1,X2,…,Xm},其中Xi表示X方中的第i个匹配主体,i∈I={1,2,…,m},m≥2;Y方主体集Y={Y1,Y2,…,Yn},其中Yj表示Y方中的第个匹配主体,j∈J={1,2,…,n},n≥2。
定义3[8,15]设μ:X∪Y→X∪Y映射,若n≥m≥2,对∀Xi∈X,Yj∈Y,满足下列条件:(i)μ(Xi)∈Y,μ(Yj)∈X∪{Yj};(ii)μ(Xi)=Yj,μ(Yj)=Xi,称Xi和Yj在μ中匹配,记为(Xi,Yj),其中μ(Yj)=Yj表示Yj在μ中未匹配。若∀(Xi,Yj)∈μ,满足μ(Xi)≠Yj′,Yj′∈Y,Yj′≠Yj,μ(Yj)≠Xi′,Xi′∈X,Xi′≠Xi,称μ是一对一双边匹配。
1.2 问题描述
考虑直觉模糊偏好信息下的一对一双边匹配问题,下面给出双边匹配的基本设置。
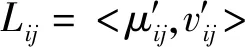
本文需要解决的问题是:在考虑双边主体后悔规避心理行为和匹配意愿情形下,依据双边主体的直觉模糊偏好向量Ti(i∈I)和Lj(j∈J),建立双边匹配模型,获得双边匹配方案。
2 匹配满意度
为解决上述双边匹配问题,本文依据后悔理论的思想,通过一方主体对另一方主体进行两两比较,计算每个主体的后悔值和欣喜值,进而计算每个主体相对于其他所有主体的总体后悔欣喜值,构建匹配满意度计算规则。下面构造效用函数和后悔-欣喜函数。
2.1 效用函数
首先将双边主体的直觉模糊偏好信息转化为效用值,基于直觉模糊数的距离测度和贴近度的思想,构造如下的效用函数。
其中,x=<μ,v>是直觉模糊数,x+=<1,0>,x-=<0,1>。f∈[0,1],当x趋近于x+时,f趋近于1,当x趋近于x-时,f趋近于0。特别地,当x=x+时,f=1,当x=x-时,f=0。
设u(Tij)是直觉模糊偏好信息Tij的效用值,其计算公式为
(1)
其中,u(Tij)∈[0,1],当Tij趋近于x+时,u(Tij)趋近于1,当Tij趋近于x-时,u(Tij)趋近于0。特别地,当Tij=x+时,u(Tij)=1,当Tij=x-时,u(Tij)=0。
设u(Lij)是直觉模糊偏好信息Lij的效用值,其计算公式为
(2)
其中,u(Lij)∈[0,1],当Lij趋近于x+时,u(Lij)趋近于1,当Lij趋近于x-时,趋近于0。特别地,当Lij=x+时,u(Lij)=1,当Lij=x-时,u(Lij)=0。
2.2 后悔-欣喜函数
由于双边主体对于后悔和欣喜都是风险规避的,考虑单调递增的凹函数作为后悔-欣喜函数[20]。本文采用指数函数作为后悔-欣喜函数。R(Δu)=1-exp(-δΔu),其中,R(Δu)是关于Δu的单调递增凹函数,Δu表示效用值的差值,R(0)=0。当R(Δu)≥0时,R(Δu)表示欣喜,当R(Δu)<0时,R(Δu)表示后悔,当Δu>0时,有|R(-Δu)|>R(Δu)成立,即双边主体是后悔规避的。参数δ(δ>0)是后悔规避系数,且δ越大,表明双边主体的后悔规避程度越大[20]。
设主体Xi和主体Yj匹配相对于和主体Yk匹配的后悔值为Fi(Yj,Yk),其计算公式为

(3)
设主体Xi和主体Yj匹配相对于和主体Yk匹配的欣喜值为Gi(Yj,Yk),其计算公式为
(4)
其中,δi是主体Xi的后悔规避系数,且δi越大,表明主体Xi的后悔规避程度越大。
主体Xi和主体Yj匹配相对于和Y方中其他主体匹配的总体后悔欣喜值为
(5)
其中,Vij表示主体Xi和主体Yj匹配关于后悔和欣喜的总体心理感知,且Vij越大,表明主体Xi对主体Yj的满意度越大。
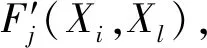
(6)
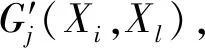
(7)
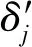
主体Yj和主体Xi匹配相对于和X方中其他主体匹配的总体后悔欣喜值为
(8)
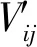
设主体Xi对主体Yj的匹配满意度为αij,主体Yj对主体Xi的匹配满意度为βij,其计算公式分别为
(9)
(10)
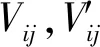
为了便于下文的讨论,在双边匹配满意度的基础上给出双边匹配差异度的定义。
设xij为0-1变量,其中xij=0表示Xi和Yj不匹配,xij=1表示Xi和Yj匹配。
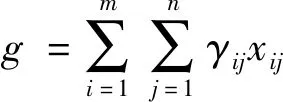
3 双边匹配方法
在本节中,首先建立双边匹配多目标优化模型;然后考虑双边主体的匹配意愿,将多目标优化模型转化为单目标规划模型进行求解;最后提出一种改进的匹配意愿系数确定方法。
3.1 双边匹配模型
以最大化每方主体的匹配满意度为目标,建立双边匹配多目标优化模型:
(11)
(12)
(15)
在上述模型中:式(11)表示最大化X方对Y方主体的满意度;式(12)表示最大化Y方对X方主体的满意度;式(13)表示每个X方主体至多与Y方中的一个主体匹配;式(14)表示每个方主体Y至多与X方中一个主体匹配;式(15)表示双边匹配数量约束。
模型(11)~(15)目标函数的量纲量级相同,使用线性加权法将其转化为单目标规划模型:
(16)
其中,ωX和ωY分别是目标函数Z1和Z2的权重系数,满足ωX+ωY=1,0<ωX,ωY<1。
基于优化模型的双边满意匹配方法获得的匹配解大多是部分最优解,即在获得的双边匹配对中可能会出现一方匹配主体的满意度较高,而另一方匹配主体的满意度较低的不公平匹配现象[17,18,22]。为解决该问题,乐琦[17,18]考虑双边主体的匹配意愿,构建基于匹配意愿的双边满意匹配优化模型;王中兴等[22]基于匹配满意度的互补性和一致性,建立基于调节参数的组合优化模型。
考虑双边主体的匹配意愿[17,18]将模型(16)~(19)扩展为如下的线性规划模型:
(20)
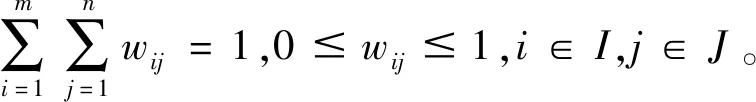
3.2 改进的匹配意愿系数确定方法
文献[17,18,22]提出的方法对解决基于优化模型的双边满意匹配方法部分最优解的不足问题提供了可借鉴的思路和方法支撑。文献[22]方法中调节参数的确定带有主观性,在实际应用中可操性不强。文献[17,18]分别提出基于得分差异度的匹配意愿系数确定方法,获得规范化的匹配意愿系数分别为式(24)和式(25)所示:
(24)
(25)
注1文献[17,18]构建基于直觉模糊得分函数的匹配优化模型,该得分函数相当于本文中的满意度函数,式(24)~(25)中的满意度对应于文献[17,18]中的得分值。
从式(24)和式(25)可以看出:1)双边主体的匹配意愿系数wij仅与匹配差异度γij相关,且与γij呈负相关关系;2)当γi′j′=γij,i′≠i,j′≠j,i′,i′∈I,j′,j∈J时,则wi′j′=wij,即匹配差异度相同的双边主体对应的匹配意愿系数相同。结论1)和2)与实际匹配情况不一致,下面通过一个例子来说明。
例1设X方主体集为{X1,X2,X3},Y方主体集为{Y1,Y2,Y3},双边满意度矩阵如下所示:
1)SIFT,该算法用于检测斑点;2)SURF,该算法用于检测斑点;3)ORB:该算法代表带方向的 FAST 算法与具有旋转不变性的 BRIEF 算法。
其中,αij是Xi对Yj的满意度,βij是Yj对Xi的满意度,i,j=1,2,3。
依据式(24)和式(25)计算获得双边主体的匹配差异度和匹配意愿系数为
从双边主体的满意度矩阵和匹配差异度矩阵可以看出:1)X1和Y2彼此间的满意度均为最高(α12=β12=1.00),X1和Y1彼此间的满意度均较高(α11=β11=0.80),X1和Y3彼此间的满意度均为最低(α13=β13=0.40)。因此,X1和Y2相匹配的意愿最高,X1和Y1相匹配的意愿次之,X1和Y3相匹配的意愿最低。根据式(24)和式(25)的计算结果,则上述双边主体对应的匹配意愿系数皆相同(w12=w11=w13=0.126[17],w12=w11=w13=0.148[18]);2)X3和Y3彼此间的满意度均较高(α33=0.90>α13=0.4,β33=1.00>β13=0.4),因此,X3和Y3相匹配的意愿高于X1和Y3相匹配的意愿,根据式(24)和式(25)的计算结果,后者的匹配意愿系数大于前者的匹配意愿系数(w13>w33[17,18])。显然,1)和2)与实际匹配情况不一致。
社会交换理论表明双边匹配实质上是一种资源的交换行为,匹配成功的条件不仅取决于于匹配双方具备相近的满意度,而且取决于匹配双方彼此间的满意度大小。双边主体匹配意愿的含义是:匹配双方彼此间的满意度越高,且匹配差异度越小,双方相匹配的意愿就越高,反之,双方相匹配的意愿就越低。因此,双边主体的匹配意愿系数不仅与匹配差异度有关,且与满意度密切相关。下面给出一种新的匹配意愿系数确定方法。
考虑双边主体的匹配满意度和匹配差异度,构建如下的匹配意愿系数优化模型:
(26)
为求解上述模型,构造如下的拉格朗日函数:
(27)
对拉格朗日函数关于ωij,i∈I,j∈J和λ求偏导,并令其为零,则
求解上述方程组,获得最优解,其中
(28)
(29)
依据式(29)可以得出:1)双边主体的匹配意愿系数wij和双边满意度(αij+βij)以及匹配差异度γij相关,且与(αij+βij)呈正相关关系,γij与呈负相关关系;2)当双边主体的匹配差异度相等时,双边满意度越大,双边主体的匹配意愿系数也越大,反之亦然。
为了说明本文匹配意愿系数确定方法的合理性,下面使用本文方法对例1进行求解,获得双边主体的匹配差异度和匹配意愿系数如下所示:
由上知:w12=0.174>w11=0.139>w13=0.070,且w33=0.150>w13=0.070,这X1与Y2和相匹配的意愿最高,X1与Y1相匹配的意愿次之,X1与Y3相匹配的意愿最低以及X3与Y3相匹配的意愿高于X1与Y3相匹配的意愿的实际情况相一致。
综上所述,考虑后悔规避与匹配意愿的直觉模糊双边匹配方法的计算步骤如下:
步骤1依据式(1)~(2)将双边主体的直觉模糊偏好信息转化为效用值;
步骤2依据式(3)~(5)和式(6)~(8)计算双边主体的总体后悔欣喜值;
步骤3依据式(9)~(10)计算双边主体的匹配满意度;
步骤4依据式(29)计算双边主体的匹配意愿系数;
步骤5建立双边匹配模型(11)~(15),将其扩展为模型(20)~(23);
步骤6通过求解模型(20)~(23),获得双边匹配方案。
4 算例分析
考虑服务外包供需匹配问题。CS服务外包网是专门从事为服务外包发包企业和接包企业提供信息和撮合服务的第三方非营利性平台。某季度,CS收到4家企业X1,X2,X3,X4关于业务流程外包(BPO)的发包信息和5家企业Y1,Y2,Y3,Y4,Y5关于业务流程外包的接包信息。发包企业的外包专家小组依据服务质量、服务价格、服务响应和管理能力等对接包企业进行综合评价,采用投票方式和统计分析方法给出5家接包企业的直觉模糊偏好信息,如表1所示。接包企业的接包专家小组依据服务内容、服务技术水平、服务方式和企业信誉等对发包企业进行综合评价,采用投票方式和统计分析方法给出4家发包企业的直觉模糊偏好信息,如表2所示。CS依据发包企业和接包企业的偏好信息对双方进行优化匹配。

表1 发包企业给出的关于接包企业的直觉模糊偏好信息

表2 接包企业给出的关于发包企业的直觉模糊偏好信息
4.1 计算过程
为解决上述双边匹配问题,采用前文提出的方法,下面给出计算过程和结果。
首先依据式(1)~(2)将双边主体的直觉模糊偏好信息转化为效用值,获得双边主体的效用值矩阵分别为
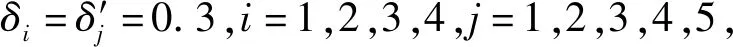
依据式(9)~(10)计算双边主体的满意度,获得双边主体的满意度矩阵分别为
建立双边匹配多目标优化模型(11)~(15),依据式(29)计算双边主体的匹配意愿系数,采用等权重线性加权法(为了便于下文作对比,取ωX=ωY=1)将多目标优化模型(11)~(15)扩展为单目标规划模型(20)~(23),并使用软件LINGO 11.0求解,可得Z*=0.4564,x11=x22=x35=x44=1,其余xij=0。
即发包企业X1和接包企业Y1匹配,发包企业X2和接包企业Y2匹配,发包企业X3和接包企业Y5匹配,发包企业X4和接包企业Y4匹配,接包企业Y3未匹配。
4.2 结果分析
为了说明本文方法的合理性,下面采用文献[17,18]的方法对上述双边匹配问题进行求解,获得的双边匹配结果如表3所示。从表3可以看出:文献[17,18]的双边匹配结果相同,本文的双边匹配方案与文献[17,18]的方案不完全一致,且对应的单边匹配满意度(目标函数值Z1和Z2)、匹配差异度(g)皆优于文献[17,18]的结果。产生这种差异的主要原因在于:文献[17,18]构建基于得分函数的匹配满意度,建立基于期望效用理论的双边匹配模型,忽略了直觉模糊偏好中的犹豫度信息和双边主体的有限理性行为;本文构建基于直觉模糊距离测度的效用函数以及考虑双边主体的后悔规避心理行为,建立基于后悔理论的双边匹配模型,因此,挖掘和利用了直觉模糊偏好中的犹豫度信息以及匹配主体关于后悔和欣喜的心理感知。

表3 不同双边匹配方法的对比
5 结语
本文针对直觉模糊偏好信息的双边匹配问题,考虑匹配主体的后悔规避心理行为和匹配意愿,基于直觉模糊距离测度和贴近度的思想构造效用函数,依据后悔理论,通过一方主体将另一方主体进行两两比较,获得每个主体的总体后悔欣喜值,建立双边匹配多目标优化模型,为解决现有匹配意愿系数确定方法的不足问题,提出一种改进的匹配意愿确定方法,考虑双边主体的匹配意愿,将多目标优化模型转化为单目标规划模型进行求解。本文为解决考虑匹配主体心理行为的双边匹配问题,提供了一种新的思路和方法。进一步的工作是研究考虑匹配主体参照依赖和损失规避心理行为的直觉模糊双边匹配问题。
