预压弯简支钢-混凝土组合梁桥应力计算方法
2020-11-10岳俊欢张文彬杨忠恒
岳俊欢,李 睿,张文彬,杨忠恒
(1.昆明理工大学 建筑工程学院,云南 昆明 650500;2.普洱市地方公路管理处,云南 普洱 665000)
对于钢-混组合梁桥而言,尽管传统的钢-混组合梁能够满足桥梁使用和通行的要求,但随着人们对桥梁受力性能和组合效益的日益重视,以及预压弯技术的不断成熟,在钢-混组合梁桥中施加预弯技术,已经在实际工程中得到了广泛应用。
针对钢-混组合梁桥,桥梁的设计内力目前均采用弹性分析法或弹性有限元方法确定,计算时常采用弹性设计法、弹塑性设计法以及塑性设计法[1~8]。对预弯钢-混组合梁的计算方法研究相对较少,相较于传统的预弯梁,由于预压弯组合梁的混凝土板在钢梁的上缘,因此在预弯的方法和目的上均与前者不同,对该类桥的计算方法研究更少。针对预压弯钢-混组合简支梁桥在计算方法上进行研究,具有一定的价值[9~11]。
本文在预弯钢-混组合梁桥相关理论的基础上,自行推导出预压弯钢-混组合简支梁截面正应力以及结合面剪应力的计算方法,结合工程实例建立有限元模型,将理论计算结果与有限元计算结果进行对比得出结论;同时也将传统的钢-混组合简支梁桥与预压弯钢-混组合简支梁桥的相关应力结果进行对比,并得出相关结论。
1 预压弯钢-混组合梁的受力特点
与传统的钢-混组合梁桥不同,预压弯钢-混组合梁桥在钢裸梁阶段,便在其两个四分点上施加使钢梁产生正弯矩的预弯力(即压弯力),随之浇筑混凝土顶板,待混凝土顶板至一定强度后,施加二期荷载,然后卸除预弯力,梁体反弹,随即形成预压弯钢-混组合梁桥。因此在钢梁的回弹下混凝土顶板会产生拉应力,所以预压弯钢-混组合梁桥的桥面板混凝土通常采用受拉性能相对较好的钢纤维混凝土[12~14],同时钢梁与混凝土板间产生逆向剪切应力(即该剪应力方向与桥梁恒、活荷载产生剪应力方向相反)。相较于传统的钢-混组合梁桥,预压弯简支钢-混凝土组合梁桥在施工阶段及成桥后,其顶板混凝土压应力、钢-混结合面剪应力、抗剪连接件的受力明显较小,由于对钢梁的预弯,其钢梁下缘的拉应力会略大,更充分地发挥了钢材的抗拉性能。
2 预压弯简支钢-混凝土组合梁的应力计算方法
由于预压弯钢-混组合简支梁本质属于预弯梁,其基本假定和思路与预弯梁大致相同。在预弯梁的基本假定和思路基础上,结合简支钢-混组合梁的结构[15~19],提出预压弯简支钢-混组合梁以弹性应力分析为基础的计算方法,即弹性叠加法的计算思路。公式推导前作以下假定:(1)各受力阶段截面变形均符合平截面假设;(2)钢材和混凝土均为理想的弹性材料,应力-应变符合胡克定律;(3)受压区混凝土在全部恒载作用下保持受拉状态但不开裂,而在活载标准值作用下混凝土为受压状态。
推导出的预压弯简支钢-混组合梁桥的预拱度计算公式如式(1);在不考虑混凝土收缩和徐变的标准组合下钢梁和混凝土跨中截面应力计算公式如式(2)~(5);成桥后支点与预弯力加载点之间的结合面剪应力计算公式如式(3)~(6)。
预拱度:
(1)
式中:f0为钢梁的预拱度;Es为钢梁材料的弹性模量;P0为预弯力;l0为预压弯简支钢-混组合梁的计算跨径;qs为钢梁的自重集度;Is为钢梁绕其重心轴的截面惯性矩。
钢梁上缘应力:
(2)
钢梁下缘应力:
(3)
混凝土上缘应力:
(4)
混凝土下缘应力:
(5)
式中:σsU为标准组合下跨中截面钢梁顶部应力;σsL为标准组合下跨中截面钢梁底部应力;σcU为标准组合下跨中截面混凝土顶部应力;σcL为标准组合下跨中截面混凝土底部应力;Mh为最不利活载作用下跨中位置的弯矩,Mh=Mq+Mr,Mq为由汽车荷载引起的计算截面弯矩标准值;Mr为由人群荷载引起的计算截面弯矩标准值;Mg3为二期铺装荷载作用下跨中位置的弯矩;nE为钢梁与混凝土弹性模量之比;I1为预压弯简支钢-混组合梁换算截面惯性矩;Mg1为钢梁自重在跨中截面产生的弯矩;Mg2为钢筋混凝土桥面板重力引起的弯矩标准值;My为预弯力在跨中截面产生的弯矩;ysU,ysL为钢梁截面形心到钢梁上、下缘的距离;Is为钢梁的截面惯性矩;ycU1为预压弯简支钢-混组合梁换算截面重心轴到钢纤维混凝土顶的距离(见图1)。
其余参数见图1(图中:G1为预弯组合梁的截面形心;Gc为混凝土截面的形心;Gs为钢梁截面形心)示。
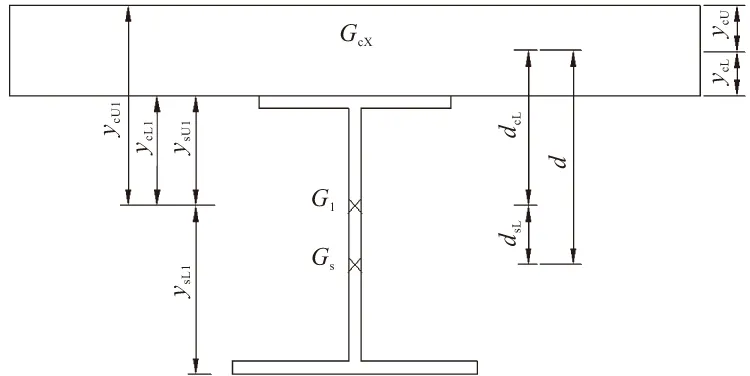
图1 预弯组合梁截面参数
结合面剪应力:
(6)
式中:P0为设计预弯力;τlz为由P0和外荷载共同作用引起的纵向剪应力;b1为钢梁顶板宽度;Vd为作用于组合梁上的外荷载剪力设计值,按荷载作用的标准组合取值;S为钢纤维混凝土换算截面绕整个预压弯简支钢-混组合梁换算截面重心轴的静矩。
3 工程概况及有限元模型建立
3.1 工程概况
昆明市二环石虎关立交桥至大观河桥段高架桥,全线现有主线桥298跨,长6.534 km,原有桥梁的上部结构为预制空心板、现浇预应力混凝土箱梁的形式。现因交通和安全需求,对石虎关立交桥至大观河桥段高架桥及匝道上部结构拆除重建,上部结构重建为钢箱梁和简支钢-混组合梁,结构简支,桥面连续。跨径长30 m,桥面宽12.75 m,采用5片30 m钢板组合梁通过横向连接而成。钢纤维混凝土桥面板采用主梁与钢纤维混凝土桥面板通过剪力钉连接,如图2~ 4所示。

图2 1/2组合梁立面/mm
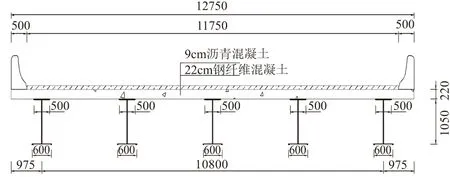
图3 组合梁端部截面/mm

图4 组合梁中部截面/mm
其中,钢梁采用Q345c钢材,容重为77 kN/m3,弹性模量为2.06×105MPa;混凝土采用CF40钢纤维混凝土,根据JTG 472-2015《钢纤维混凝土》,钢纤维混凝土受压和受拉弹性模量以及剪切变形模量,可采用与钢纤维混凝土等级相同的普通混凝土的弹性模量,所以CF40钢纤维混凝土容重为26 kN/m3,钢纤维掺入量为100 kg/m3,弹性模量为3.25×104MPa,泊松比0.2,轴心抗压强度标准值26.8 MPa,较普通混凝土,抗拉强度可提高40%~80%。
3.2 有限元模型建立
现以30 m跨径简支钢-混组合梁为例,分别建立传统的钢-混组合简支梁和预压弯钢-混组合简支梁两个模型,模型中的钢纤维混凝土桥面板采用3D实体单元建立,钢梁采用2D平面单元建立,钢梁上顶板印刻于混凝土板上。对于混凝土顶板,网格划分为100 mm边长的正六面体单元;对于钢板梁,各片钢板网格划分为100 mm边长的四边形平面单元。为保证预压弯简支钢-混组合梁和普通简支钢-混组合梁的计算结果更有可比性和说服力,二者模型建模时保持完全一致,仅通过控制施工阶段的不同来实现梁体的预弯效果,如图5所示。

图5 中梁模型示意
4 计算结果对比分析
4.1 预压弯简支钢-混组合梁理论计算与模型计算对比分析
为验证本文提出的预压弯简支钢-混组合梁的预拱度计算公式、弯曲应力和结合面剪应力的理论计算方法,用式(1)(3)(4)(6)分别计算出预拱度、成桥阶段钢梁下缘最大拉应力、成桥阶段混凝土上缘最大平均压应力和结合面最大横向平均剪应力,并与建模计算结果进行对比分析,如表1所示。
分析表1,可看出本文提出的预压弯简支钢-混组合梁的预弯力计算方法、预拱度计算值、弯曲应力和结合面剪应力的理论计算值与模型运行结果吻合较好,验证了本文理论计算方法的可行性,进一步证实了本文提供的理论计算方法是较为准确的。预拱度理论计算偏小,其原因是模型钢梁因端部截面较小而导致模型刚度较小;而混凝土板应力计算结果偏差较大,是因为混凝土板宽度较大,剪力滞后效应导致横桥向剪应力不相等,剪力滞后效应较为明显而导致的。
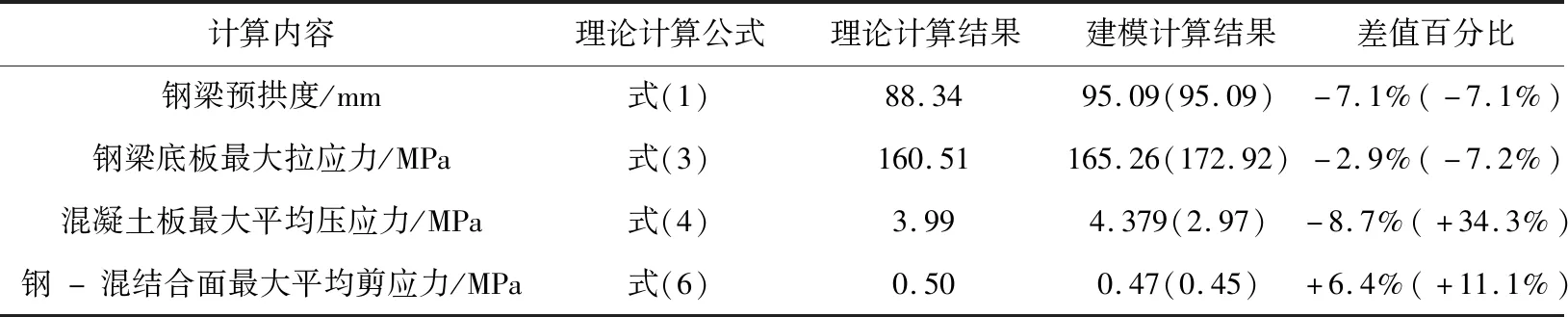
表1 预压弯简支钢-混组合梁理论计算与建模计算结果对比
4.2 预压弯简支钢-混组合梁和传统简支钢-混组合梁分析结果对比
为对比预压弯简支钢-混组合梁和传统简支钢-混组合梁的计算结果,取跨中截面的混凝土板最大拉、压应力、钢梁底板最大拉应力作为正应力控制值,梁端处钢-混结合面剪应力作为剪应力控制值,归纳总结如表2所示。为模拟结构的真实受力状态,在建模时计入混凝土的长期收缩徐变影响,同上提取各应力控制值见表3。
分析表2可知,预压弯简支钢-混组合梁的混凝土压应力与结合面剪应力仅为传统简支钢-混组合梁的50%左右。故当以混凝土压应力或结合面剪应力控制组合梁设计承载力时,预压弯钢-混组合梁在同样的结构参数情况下,承载力将提升一倍左右。分析表3可知,在考虑混凝土收缩徐变作用后,预压弯简支钢-混组合梁的混凝土压应力与结合面剪应力会有所折减,但预压弯钢-混组合梁的应力改善效果依旧显著。
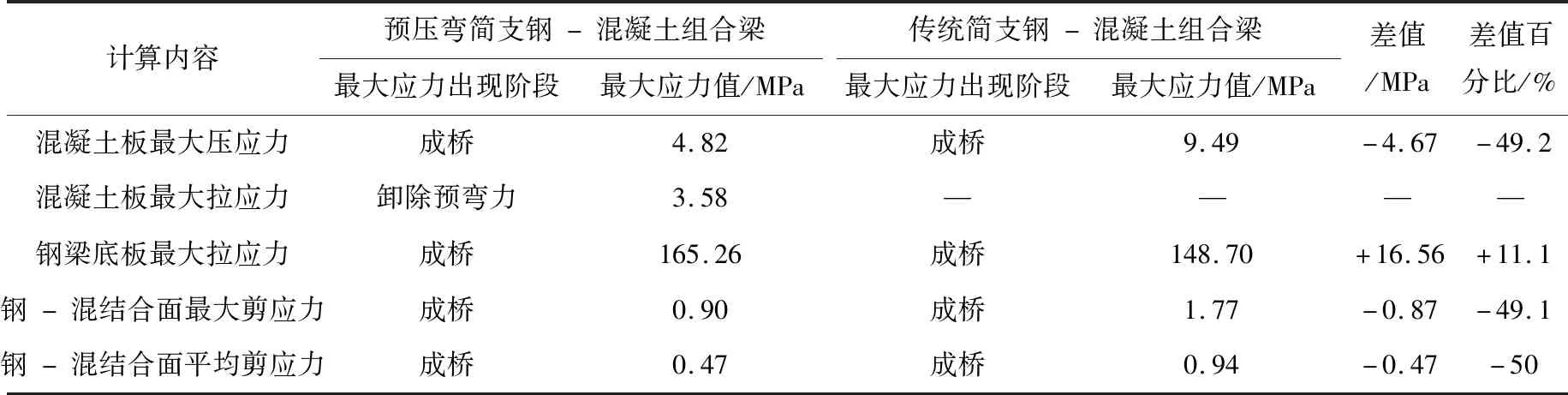
表2 预压弯简支钢-混组合梁与传统简支钢-混组合梁有限元计算结果对比
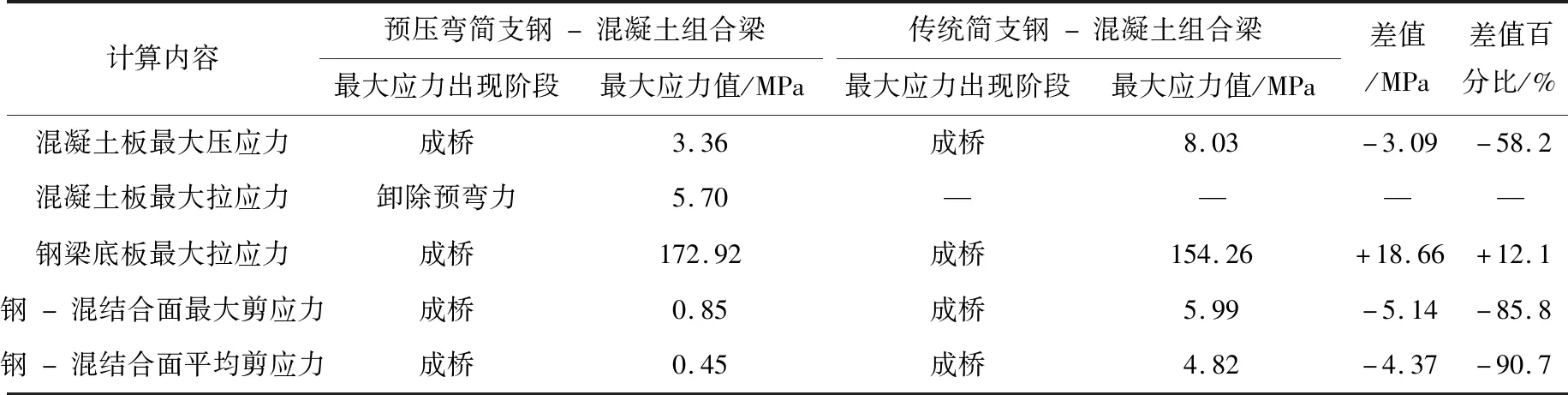
表3 预压弯简支钢-混组合梁与传统简支钢-混组合梁有限元计算结果对比(考虑混凝土长期收缩徐变)
5 结 论
本文提出了预压弯简支钢-混组合梁桥的基本假设与计算方法,并给出了预压弯简支钢-混组合梁桥的应力计算公式,通过建立有限元模型对比分析,得出以下结论:
(1)有限元软件建模计算与理论方法计算的结果对比吻合度较高,证明了自行推导出的应力计算公式较为准确。
(2)通过有限元软件建模模拟传统简支钢-混组合梁与预压弯简支钢-混组合梁受力情况,论证了预压弯简支钢-混组合梁的混凝土最大压应力、结合面最大剪应力和平均剪应力都明显小于普通简支钢-混凝土组合梁。
(3)通过提前对钢梁预弯,预压弯简支钢-混凝土组合梁桥钢梁下缘拉应力会略大于传统简支钢-混凝土组合梁桥,更加充分地发挥了钢材的抗拉特性。当以混凝土压应力或结合面剪应力控制组合梁设计承载力时,预压弯钢-混组合梁在同样的结构参数情况下,承载力有显著提升。
