考虑不同桩土效应分析模型的双座串联斜拉桥动力特性分析

黄鸣柳，沈文爱，胡宇航，朱宏平，何友娣

(1.华中科技大学 土木工程与力学学院，湖北 武汉 430074；2.中铁大桥勘测设计院集团有限公司，湖北 武汉 430056)

斜拉桥因其跨越能力强，受力合理，造型多样美观等优点，而成为大跨径桥梁的优选桥型之一。国内外目前已经建成的主跨跨度在200 m以上的斜拉桥超出了200座，其中主跨跨度超过400 m的也有40余座。随着大跨度斜拉桥的快速发展，其动力特性的复杂性以及抗震规范不够完善等问题会对分析结果产生很大的影响[1,2]。因此，大跨度斜拉桥的动力特性分析对正确地进行桥梁的抗震设计和维护有着重要的意义。

国内外学者对大跨度斜拉桥的动力特性进行了大量研究，研究发现半漂浮体系斜拉桥具有周期长、频率低、结构柔、振型耦合的特点[3～10]。同时绝大多数半漂浮体系斜拉桥的一阶振型为一阶纵飘，有利于减小地震响应，但同时会产生较大位移[11～14]。李湛[15]对某半漂浮体系斜拉桥进行了动力特性分析和动力性能测试，结果表明这类桥型的主梁纵飘和竖弯出现较早，因此桥塔顺桥向位移和主梁竖向位移较大，地震作用下应予以重视。同时许多学者对于是否考虑桩土效应也做了一定研究，马晓昕[16]以某半漂浮体系的双幅四索面结合梁斜拉桥为例，研究其动力特性，结果表明考虑桩土相互作用后，结构整体刚度减小，周期会有所延长。陈永健等[17]以某半漂浮斜拉桥为背景，研究了考虑桩土作用对斜拉桥动力特性的影响，研究发现，考虑桩土作用和不考虑桩土作用模型的低阶频率相差不大，振型也相同，但高阶频率差值变大，振型也不相同。

目前少有文献对考虑不同桩土效应分析模型的斜拉桥进行对比分析。此外，双座串联斜拉桥作为一种新型桥梁结构，目前暂时没有相关文献研究其动力特性。所以本文以在建的珠海市洪鹤大桥为研究对象，利用Midas/Civil分别建立采用五种不同桩土效应分析模型的全桥有限元模型，并研究其动力特性，对比不同模型的结果。本文可为今后大跨度斜拉桥的桩土效应分析和同类型桥梁的动力分析提供参考。

1 桩土效应分析模型

目前常用的桩土效应模型有直接嵌固法、等效嵌固法、六弹簧法、Winkler地基梁模型[18]，图1为各种模型的示意图。

1.1 直接嵌固模型

直接嵌固模型忽略桩基础和地基土对结构的影响，将桥梁承台底部直接固结。在Midas中，在桥梁承台底部节点设置约束全部自由度的一般支承来模拟直接嵌固模型。

1.2 等效嵌固模型

等效嵌固模型忽略地基土的影响，在地面或者最大冲刷线以下的一定深度处将桩基截断，并且将桩底直接嵌固。这种模型的关键在于嵌固深度的取值，目前常用取值为3倍或5倍桩径(D)[19]。在Midas中，利用梁单元分别建立3倍和5倍桩径的桩基础，在桩基础底部设置约束全部自由度的一般支承，来模拟等效3D嵌固模型和等效5D嵌固模型。

1.3 六弹簧模型

六弹簧模型是将桩基础和土体对承台的约束作用等效为承台底部六个方向的弹簧，依照规范的相关规定确定六个方向弹簧的刚度。在Midas中，通过在承台底部设置节点弹性支承，分别输入六个方向的刚度，来模拟六弹簧模型。

1.4 Winkler地基梁模型(m法)

Winkler地基梁模型中将桩基础假定为满足温克尔假定的弹性地基上的连续梁，为了考虑桩侧土的影响，将地基土对桩的水平作用简化为一系列线弹性土弹簧。等代土弹簧的刚度可根据规范的相关规定，由m法计算得到。在Midas中，利用梁单元按照实际设计长度建立桩基础，在不同深度处设置节点弹性支承，输入水平方向刚度，来模拟m法模型。

2 工程概况

珠海市洪鹤大桥主桥为分别跨越洪湾水道和磨刀门主航道的两座斜拉桥串联而成。两座斜拉桥的结构设计相同，均是桥跨布置为73+162+500+162+73 m的双塔双索面叠合梁斜拉桥。每座主桥各设置一个边墩，两个辅助墩，一个交接墩，为半漂浮体系，总体布置见图2。主梁均采用开口叠合梁，全长970 m，混凝土桥面板全宽34.9 m。主塔均采用钻石型钢筋混凝土桥塔，每个桥塔连接40对斜拉索，梁上基本索距为12 m，塔上基本索距2 m，拉索采用平行钢绞线。桩基础采用钻孔灌注桩，桩径1.8～2.8 m，桩长41～107 m。

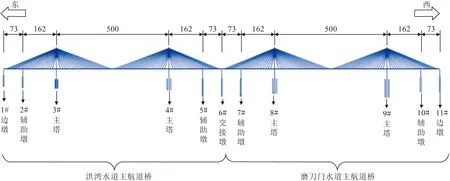
图2 桥跨总体示意/m

桥址处软土发育，软土层厚度较大，其中淤泥层平均厚度20.79 m，淤泥质粘土层平均厚度18.13 m。

3 有限元模型建立

建立准确的有限元模型是进行动力学分析的基础，不同构件的正确模拟是建立全桥有限元模型的关键。为了能够准确地模拟各个构件，需要注意刚度、质量以及边界条件的设置。本文根据不同构件的形式和受力特点，分别建立了考虑桩土相互作用的有桩模型和不考虑桩土相互作用的无桩模型，主要构件的模拟介绍见下文。

3.1 主梁、主塔和主墩的模拟

主梁计算模型根据采用模拟主梁的数量分为单主梁模式、双主梁模式和三主梁模式。由于本桥主梁截面为开口叠合梁截面，为了更好地考虑约束扭转刚度的贡献，建立三梁式模型。

主塔和主墩的模拟也采用梁单元。由于主塔形式为钻石型主塔，由塔柱和横梁组成，其中塔柱中分离的双支分别采用梁单元模拟。对于倒Y字型交接处，即双支梁与单支梁交接处，采用刚臂连接。

3.2 斜拉索的模拟

斜拉索采用Midas中的梁单元来模拟。在模拟斜拉索之前，需要计算斜拉索的密度和弹性模量，以及初应变和截面面积。建模时，将有关参数作为实常数输入软件即可。对于斜拉索由于自重垂度以及拉力引起的非线性问题，需要采用Ernst公式进行弹性模量的修正[20]。Ernst公式如下：

(1)

式中：Eeq为拉索的等效弹性模量；E为拉索材料的弹性模量；γ为拉索容重；lc为拉索的水平投影长度；σ为拉索的拉应力。

3.3 边界条件的模拟

本桥为半漂浮体系斜拉桥，塔梁和墩梁间的竖向球型支座采用弹性连接模拟，墩梁间横向C型钢阻尼器采用一般连接特性值滞后系统模拟，塔梁间纵向粘滞阻尼器采用一般连接特性值粘弹性消能器Maxwell模型模拟，阻尼器参数见表1，2；塔梁间采用约束竖向和横向的刚性连接近似模拟横向抗风支座。

表1 横向C型钢阻尼器参数

表2 纵向粘滞阻尼器参数

两桥的串联关系通过在交接墩墩顶节点上左右对称建立两个与上部主梁节点对齐的支承节点，并与墩顶节点采用刚性的弹性连接连接起来的方式实现。两个支承节点与上部主梁节点间的边界条件的设置同其他墩梁间连接。

桩土作用的边界条件按照第一部分介绍的建模方法，分别建立直接嵌固、3D等效嵌固、5D等效嵌固、六弹簧法、m法土弹簧共五种桩土效应分析模型。

根据上述建模方式，建立了全桥的有限元模型，其中无桩模型见图3，有桩模型见图4，串联处局部详图见图5。

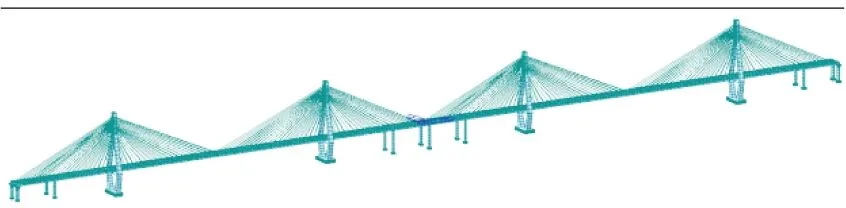
图3 全桥有限元模型(无桩)

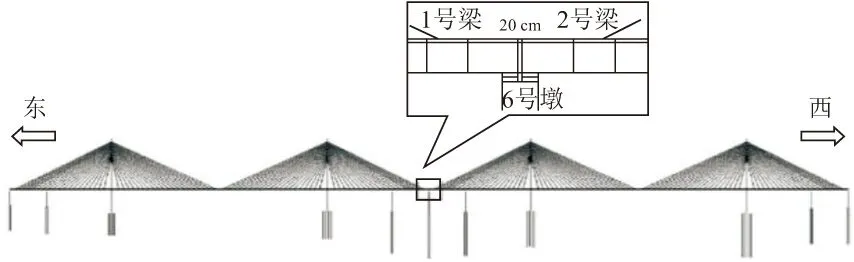
图5 串联处局部详图

4 动力特性分析

4.1 动力分析理论

对斜拉桥动力特性分析是抗震与减震分析的基础步骤，可以让我们了解斜拉桥的各阶振型和频率，了解该桥梁的固有动力特性。在桥梁的抗震设计和抗风设计等过程中，固有动力特性的计算可以帮助我们更好地了解桥梁的质量分布和刚度指标等信息，对桥梁的设计和维护意义非凡。

由于本模型单元数量大，结构复杂，利用Midas中的向量rize法进行特征值分析，为了保证结果的准确性，计算了模型前300阶模态，其中x，y，z三个方向的振型参与质量分别为94.82%，94.66%，99.97%，均达到90%以上。

4.2 动力特性分析结果

利用有限元软件分别对5种模型进行模态分析，五种模型前15阶频率及m法模型振型特征见表3，自振频率结果对比见图6，图7为m法土弹簧模型的5个典型振型。

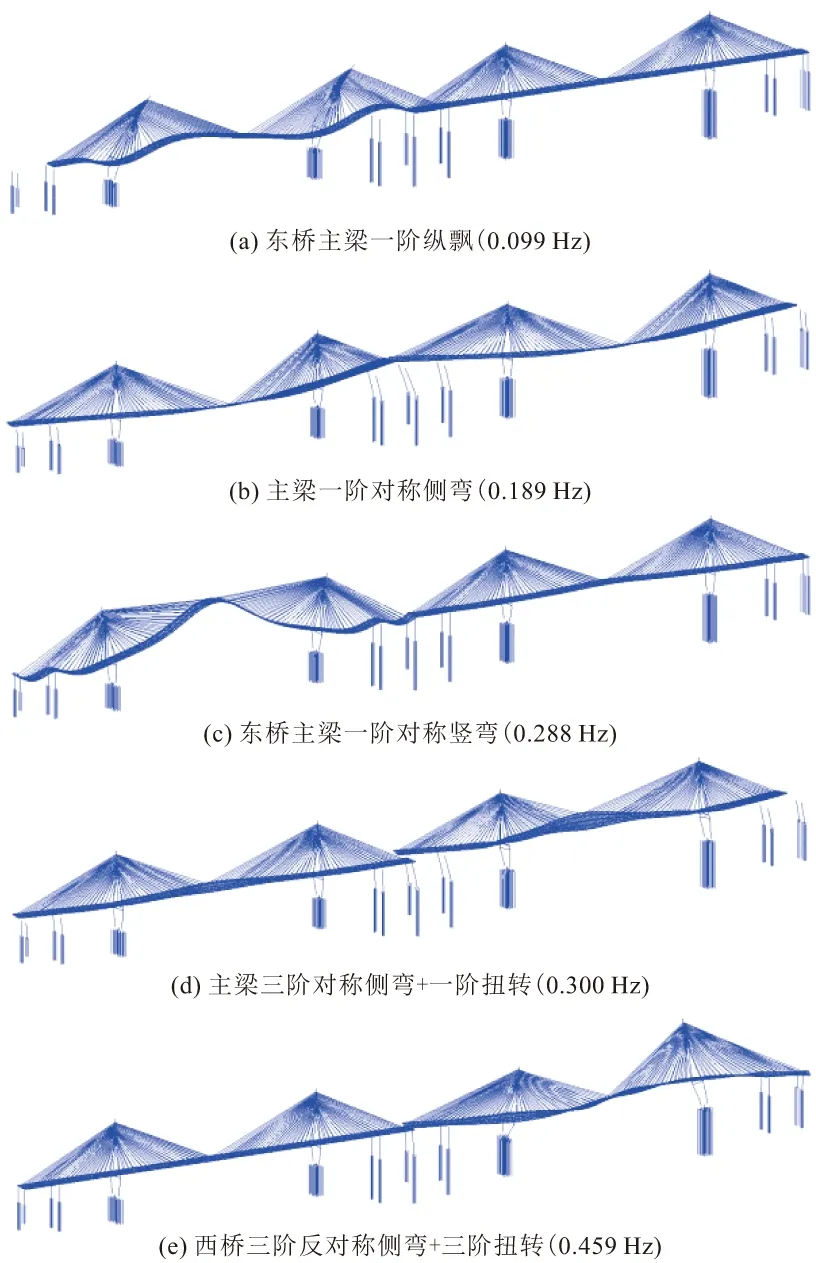
图7 洪鹤大桥主振型

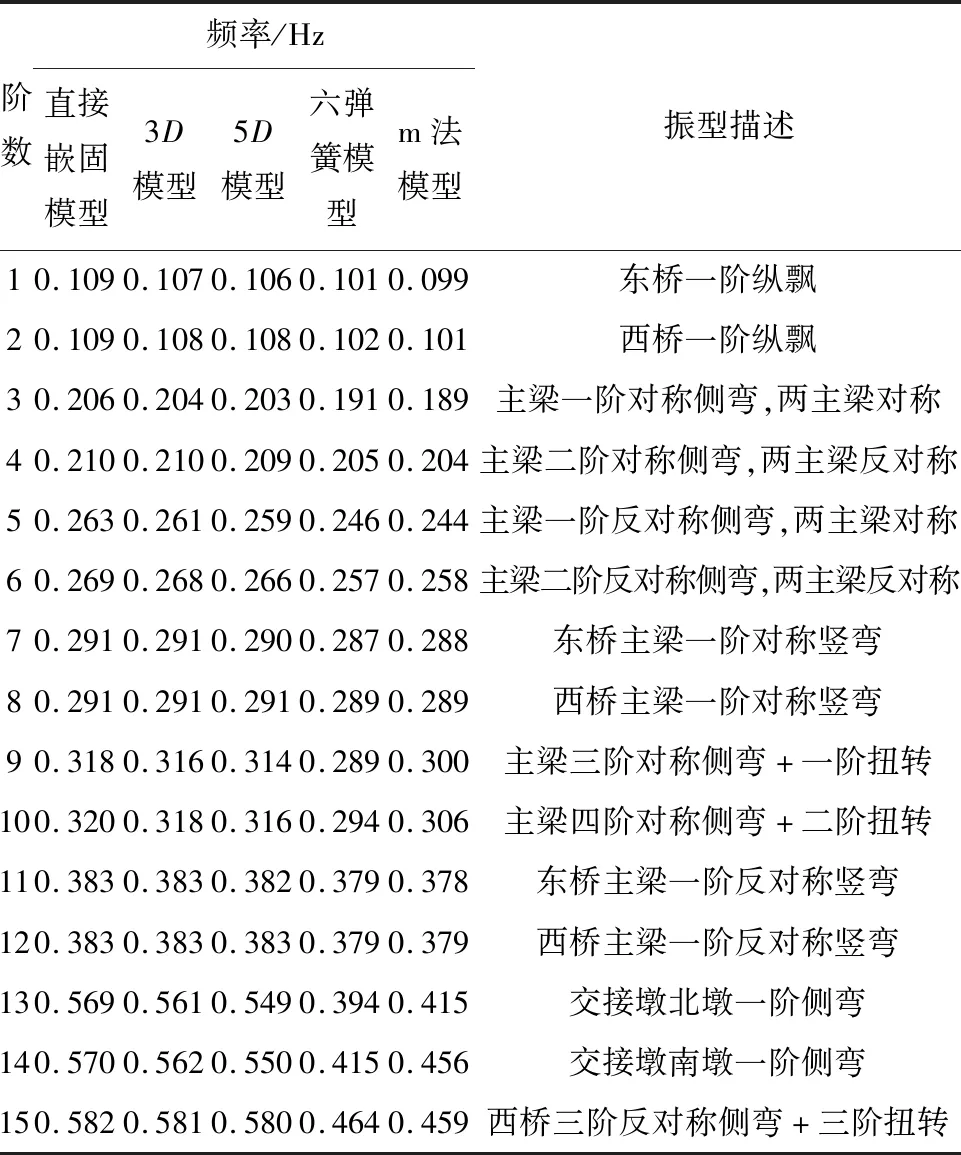
表3 洪鹤大桥前十五阶自振特性

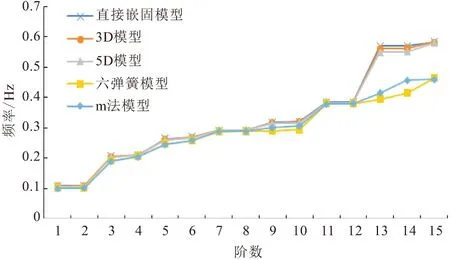
图6 五种模型频率计算结果对比

由图表可以总结得到，该双座串联大跨度斜拉桥的动力特性有以下的特点：

(1)五种模型基频分别为0.109，0.107，0.106，0.101，0.099 Hz，该桥自振频率较低，自振周期较长。同时五种模型的前15阶自振频率都在0.6 Hz以内，说明该斜拉桥的模态非常密集。

(2)桥梁前两阶主振型为主梁纵飘，符合半漂浮体系斜拉桥振型特征。

(3)主梁先出现侧弯振型而后再出现竖弯振型，并且在前15阶振型中，主梁侧弯振型出现较多。

(4)某些振型会在东西两主梁之间交替出现，如一阶纵飘、一阶竖弯、一阶侧弯等。

(5)主梁一阶扭转均出现在第九阶。同时主梁扭转振型均是与主梁侧弯相互耦合的形式出现，并没有出现单纯扭转的情况。

4.3 不同桩土效应模型对桥梁动力特性的影响

根据上节的图表，可以看出考虑不同桩土效应分析模型的结构动力特性存在一定的差异。依据对比分析结果，可以看出：

(1)对于考虑不同桩土效应分析模型的自振频率在前12阶相差不大，12阶后直接嵌固模型和等效3D和5D嵌固模型的计算结果相近，六弹簧模型和m法模型的计算结果相近。相同阶次的自振频率的大小按直接嵌固模型、3D模型、5D模型、六弹簧模型、m法模型的顺序递减。

(2)五种模型的前12阶振型基本相同，12阶后五种模型开始表现出不同的振型，同一振型出现的阶次和频率不同。

(3)直接嵌固模型和等效嵌固模型虽然建模简单，但由于没有考虑桩基础以及桩周土对桩基的影响，使结构整体刚度偏大，计算结果与实际情况不相符。

(4)六弹簧模型虽未建立桩基单元，无法考虑桩质量的惯性作用，但其利用六个方向的弹簧反映了桩土间相互作用，与实际情况相符。

(5)m法模型建立了桩基单元，并且计算了等代土弹簧刚度，可以较好地模拟桩土作用。结果与实际相符，但建模工作量较大，单元数较多，计算时间较长。

5 结 论

通过对斜拉桥动力特性的分析，可得出如下结论：

(1)本桥的动力特性与大跨度纵向半漂浮体系斜拉桥的特征符合，即自振周期较长，结构较柔，频率分布较密集。

(2)桥梁主振型为主梁纵飘，符合半漂浮体系斜拉桥结构特点，有利于减小地震内力响应，但同时会产生较大的纵向位移。在抗震设计时应注意两桥交接处是否会发生碰撞，必要时采取相应减震控制措施。

(3)桥梁的横向抗弯刚度较竖向抗弯刚度小，C型钢阻尼器不仅可以耗散地震能量，还提供了横向刚度，所以在保证结构安全的情况下，可以适当考虑调整C型钢阻尼器的参数来增大主梁横向刚度。

(4)结构主梁的抗扭刚度比抗弯刚度大。同时，在前15阶振型中，未出现单纯扭转的振型，这对该桥的抗风是有利的。这也与双座串联斜拉桥结构复杂，构件繁多的特征有关。

(5)双座串联斜拉桥的很多振型会在两桥之间交替出现，考虑是由于两座斜拉桥在纵向串联，横向并联的组合关系引起的。

(6)不同的桩土效应模型对动力特性分析结果的影响程度不同，其中直接嵌固与等效嵌固模型由于未能考虑地基土的影响，结果与m法模型相差较大。在进行软土地基上的大跨度斜拉桥的动力分析时不推荐使用这两种模型。

(7)对比考虑不同桩土效应分析模型的动力特性发现，当考虑桩-土相互作用时，结构整体周期增长，频率减小，并且会改变结构的高阶振型。所以对于大跨度斜拉桥的动力特性分析，桩土效应分析必不可少，并且需要选择准确的桩土分析模型。