一种反辐射无人机抗异步闪烁诱饵诱偏方法

张逸楠，彭世蕤，冷 毅

（空军预警学院，武汉 430019）

0 引言

反辐射无人机（anti-radiation unmanned aerial vehicle，ARUAV）是一种利用敌方雷达辐射的电磁信号发现、跟踪以至最后压制或摧毁雷达的武器系统［1-3］。当今ARUAV 的导引头上广泛采用单脉冲测角跟踪技术，在导引头设计中，为消除信号的多径效应对导引头产生的影响，多采用脉冲前沿跟踪技术［4］。为了保护雷达自身，雷达系统会利用有源诱饵装置诱偏ARUAV，这种装置利用有源诱饵和雷达构成一个有源诱偏阵，使ARUAV 接收雷达辐射信号的同时也接收诱饵辐射的诱偏信号，实现对ARUAV 的有效诱骗，以达到保护雷达的目的［5-6］。导引头采用前沿测向可进行正确测向，但测向结果将随诱饵信号前沿变化而变化，导致命中概率降低［7］。仅通过前沿跟踪，只能引导ARUAV 靠近雷达阵地，识别并剔除其中脉冲前沿超前的那个诱饵，无法从中识别出雷达［8］。因此，ARUAV 攻击配诱饵雷达系统的一种战术思想可确立为先摧毁诱饵，再攻击雷达，即ARUAV 的攻击能有效毁伤任一辐射源即可。对于抗异步闪烁诱偏而言，本文先通过分析诱饵信号与雷达信号合成的不完全重合信号幅度信息，提取单一辐射源信号存在的脉冲时刻，然后将此时刻的方位角和俯仰角转换为单一辐射源的地面位置信息，形成地面单一辐射源位置点集，并用灰色数据处理方法实时匹配地面位置信息，使ARUAV 准确跟踪某单一辐射源，达到有效毁伤至少一个辐射源的目的。算法主要作用于ARUAV 俯冲攻击以后，即ARUAV 的末制导阶段，在该阶段导引头与辐射源距离较近、且为直视，电磁波的反射或折射对导引头接收信号影响不大；另外，导引头接收的雷达信号几乎为雷达副瓣信号，其电平与诱饵信号电平基本在一个数量级［9］。

1 不完全重合信号特征及单信号识别基础

闪烁诱偏在时序上划分为同步闪烁诱偏和异步闪烁诱偏［10］，同步闪烁诱偏的诱饵按时序周期性地发射诱偏信号，在任一时刻只有一个诱饵发射诱偏信号；异步闪烁诱偏的诱饵独立地发射诱偏信号，没有时序上的严格限制，如图1 所示，诱饵信号与雷达信号的合成信号构成不完全重合信号，各部分由不同的信号合成［11］，其中，Tr为雷达脉冲重复周期，Td为诱饵合成信号的重复周期。

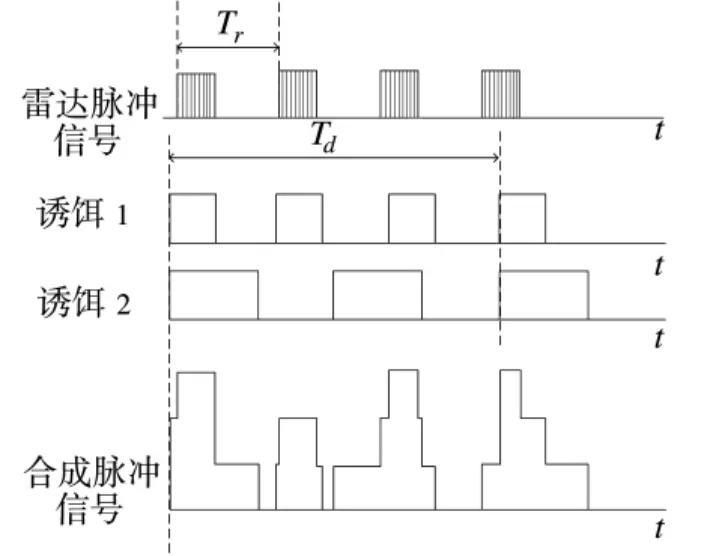
图1 雷达与诱饵信号合成脉冲

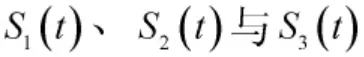
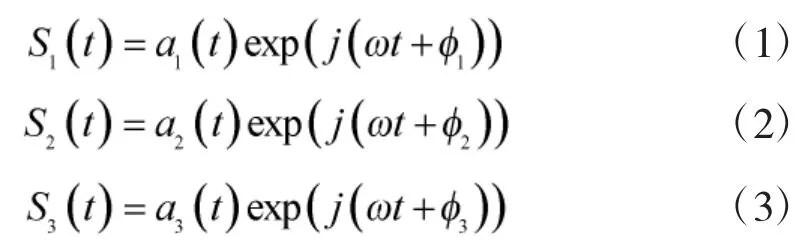
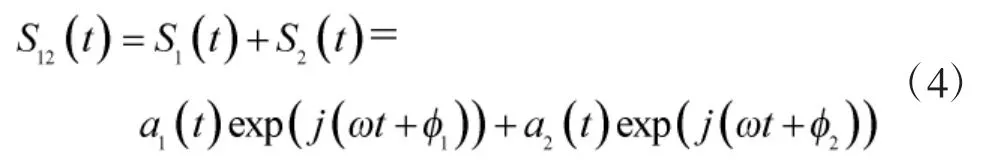
当3 个辐射信号同时到达导引头天线阵列时，导引头所接收的信号为3 个信号矢量叠加后的合成信号，将此合成信号表示为：

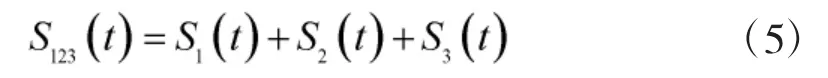
现令U1表示导引头接收到1 个辐射信号的信号幅度；U2、U3分别表示导引头接收到2 个及3 个辐射信号叠加的合成信号幅度。则：

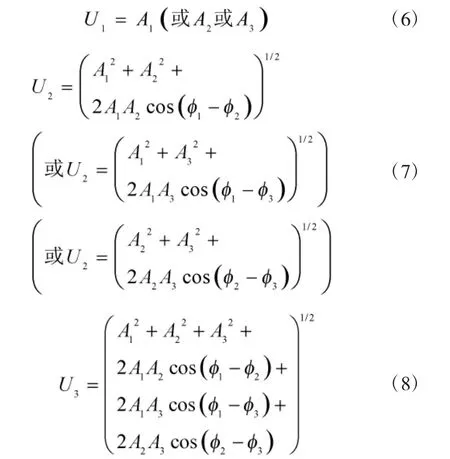
可见，当信号的瞬时幅度最大值确定后，导引头接收信号为单信号时，信号幅度为一个常值；导引头接收信号为两信号或三信号时，信号幅度随信号初值变化而变化。以此即可判断导引头在某时刻接收的不完全重合信号是否为单信号。

2 辐射源量测转换及基于灰色理论的实时匹配方法

2.1 ARUAV 末制导攻击建模

ARUAV 末制导攻击模型主要参考文献［12］中反辐射导弹运动模型的位置简化递推算法。当ARUAV 未进入俯冲攻击阶段时，作平飞运动，无俯仰面的姿态调整，仅调整方位面；当导引头框架角大于某一固定值时，ARUAV 进入俯冲攻击阶段，分别根据俯仰面与方位面的测角情况进行俯仰面与方位面的姿态调整，再进行运动的合成，最终形成ARUAV 的攻击轨迹。

2.2 量测转换

建立大地坐标系O-XYZ、机体坐标系OXmYmZm、天线坐标系O-XpYpZp与平动坐标系OXdYdZd如图2 所示，坐标系间转换关系可参考文献［12］。

设雷达及其诱饵位于XOZ 平面上，ARUAV 处于空间某点。ARUAV 测得的单辐射源角度信息用天线坐标系下单位矢量的指向表征，经过一系列坐标转换可得到其在平动坐标系下的矢量，求解这个矢量与地面的交点，可得到单辐射源在大地坐标系下的位置信息。

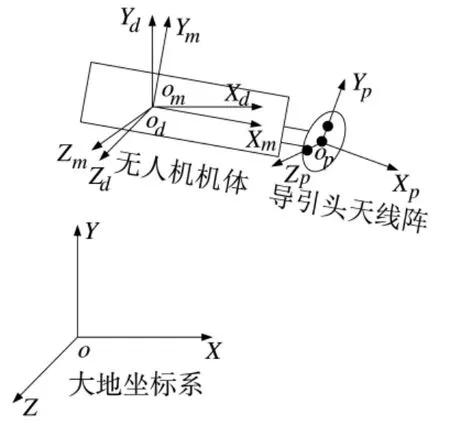
图2 4 个坐标系定义

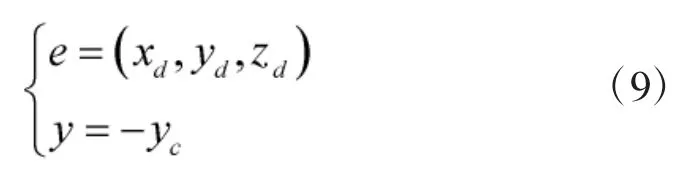
解出辐射源位置B 点在平动坐标系中的坐标后，再经过平动坐标系与大地坐标系的坐标转换矩阵，可得出大地坐标系下的辐射源位置。

图3 实时解算辐射源位置

2.3 基于灰色理论的位置信息实时匹配法

灰色系统理论主要用于求解无经验、数据较少的不确定性问题。而ARUAV 攻击配诱饵雷达系统过程中获得的数据样本量较小、分布规律随机变化，因而数据样本集是一个典型的灰色系统。

首先，确定作为参考的被估计参数x0，即某一辐射源的估计位置。可利用前几个测得的样本集二维数组各行均值的突变确定被估计值x0，该均值出现突变时，即为辐射源位置点集中某一辐射源位置与另一辐射源位置之间的转换点。因此，选取均值突变点前一个值作为被估计值x0，即随机选取了某一个辐射源的估计位置值。其中，均值突变门限的选取依据是在一定的高度、一定的导引头半波束宽度条件下，由测角误差算得的某一辐射源的位置圆概率误差。

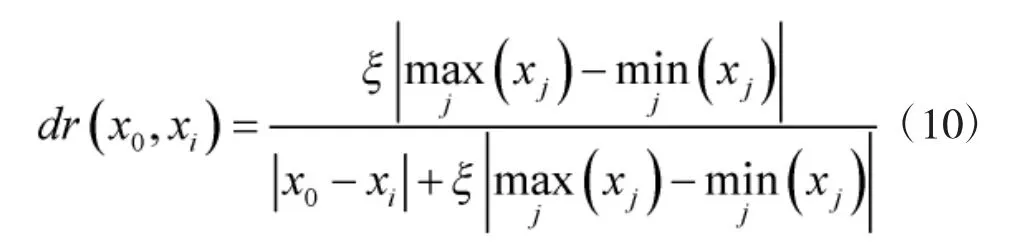
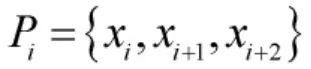
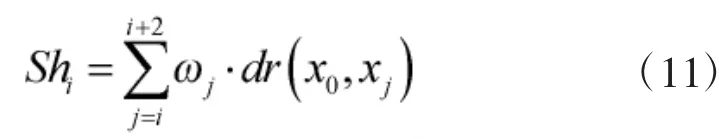
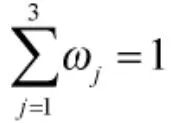
从灰色关联熵的定义可以看到，灰色关联熵是被估计值x0与样本集Pi灰色距离测度的加权求和。因此，灰色关联熵可以看作估计值与样本集之间的灰色关联度的度量，也可以看作估计值与样本集在拓扑和距离上的关联紧密程度的度量［15］。

因导引头存在测角误差，测角误差导致辐射源位置信息转换的误差，因此，导引头多次测得的同一个辐射源的位置信息将有一定的波动。由于位置误差的存在，先对各样本集内位置信息进行异常值剔除，异常值剔除步骤参考文献［13］。

剔除完各样本集内异常值后，实时计算每一组样本集与被估计值x0的灰色关联熵，计算流程如图4 所示。首先设定一个均值突变门限Δ，确定被估计值x0；然后设定灰色关联熵门限η，其选取依据是在理想条件下的各位置之间的灰色关联熵的取值，实时计算每一个样本集与被估计值x0的灰色关联熵Sh；若灰色关联熵过门限，则以此时刻导引头测得的角度作为机体姿态调整的依据，否则以储存的被估计值x0的角度作为机体姿态调整的依据。这样使ARUAV 跟踪被估计值x0所对应位置的单辐射源，最终达到对该单辐射源的毁伤目的。

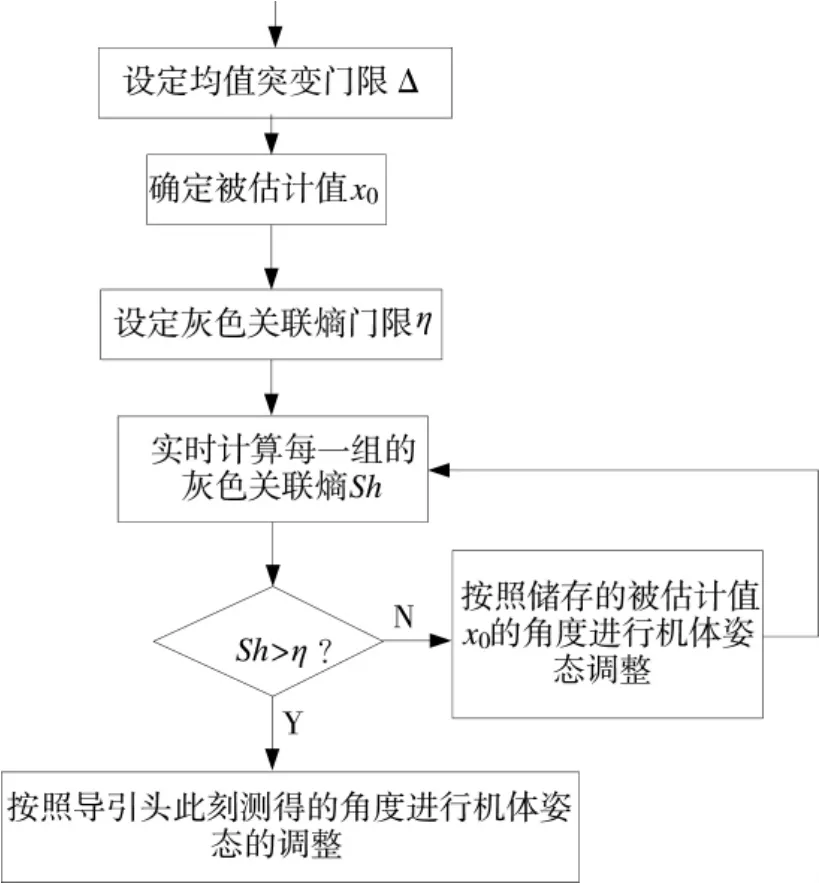
图4 位置信息实时匹配流程

3 仿真校验

3.1 ARUAV 末制导攻击建模

设ARUAV 攻击目标为一雷达配备两个异步闪烁诱饵系统，雷达与诱饵为间距300 m 的等腰三角形布阵，以使雷达及诱饵获得较高的生存概率［16］。雷达初始坐标（260 m，0 m，0 m），诱饵1（0 m，0 m，150 m），诱饵2（0 m，0 m，-150 m），如图5 所示，仿真条件为：ARUAV 初始飞行高度2 000 m，初始坐标（-4 924 m，2 000 m，868 m），设入侵角为ARUAV攻击时飞行方向在大地坐标中投影与OX 轴的夹角，本次仿真取-10°；取由噪声引起的测角误差为0.036°［17］，η=0.8，在2 000 m 高度、导引头半波束宽度60°条件下，由测角误差可算得某一辐射源的位置圆概率误差约为：Δ=1.26；设雷达与诱饵发射信号频率皆为3 GHz 且幅值函数为常值1，雷达脉冲重复周期为0.1 s，诱饵1 脉冲重复周期为0.5 s，诱饵2 脉冲重复周期为0.75 s，两个诱饵信号占空比皆为0.3，诱饵辐射场初始相位符合（-π，π）的均匀分布［18-20］；ARUAV 水平与俯仰平面分别采用双基线干涉仪比幅比相法测向体制，半波束宽度为60°，天线间间隔为0.05 m，巡航速度为50 m/s，初始天线指向角为-10°，即导引头天线阵法向与ARUAV 机身的夹角，向下为负；俯冲攻击角度为-74°，横向过载3 g，俯冲向下过载5 g，测向传输周期为0.04 s，ARUAV 机动调整周期为0.04 s。ARUAV 直接打击配异步闪烁诱饵的雷达系统的仿真如下页图5、图6 所示；ARUAV 采取文中算法打击系统进行的仿真如图7、图8 所示。

给出的两组仿真实验对比了应用算法前后的ARUAV 方位面、俯仰面测角变化情况与ARUAV 攻击航迹；算法在ARUAV 俯冲攻击后运行，主要关注ARUAV 俯冲攻击前后的测角情况。图5、图7 给出ARUAV 攻击航迹；图6、图8 给出ARUAV 测角变化情况。本次仿真中ARUAV 俯冲攻击时刻约为ARUAV 起飞后的第95 s，则截取ARUAV 飞行第75 s 到最终落地爆炸的测角变化进行说明。

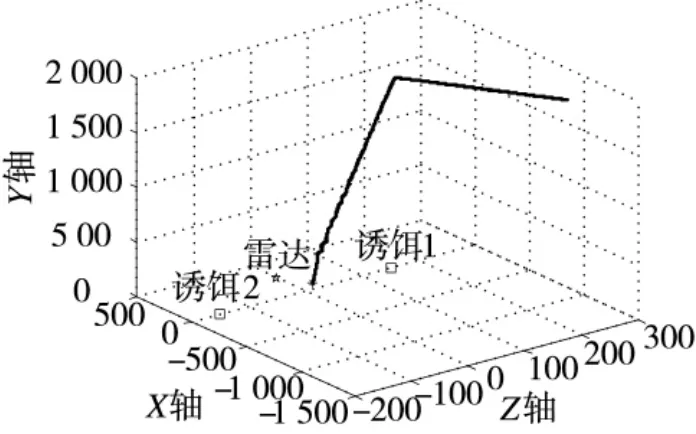
图5 无算法的ARUAV 末制导攻击情况

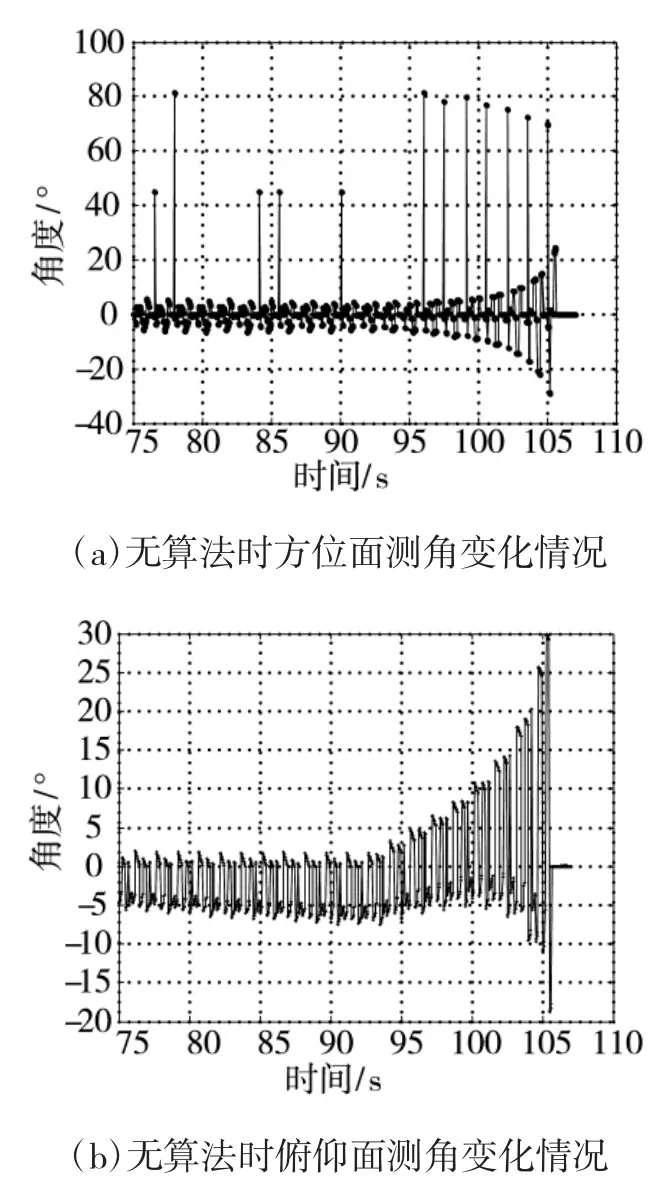
图6 无算法的ARUAV 角度变化情况

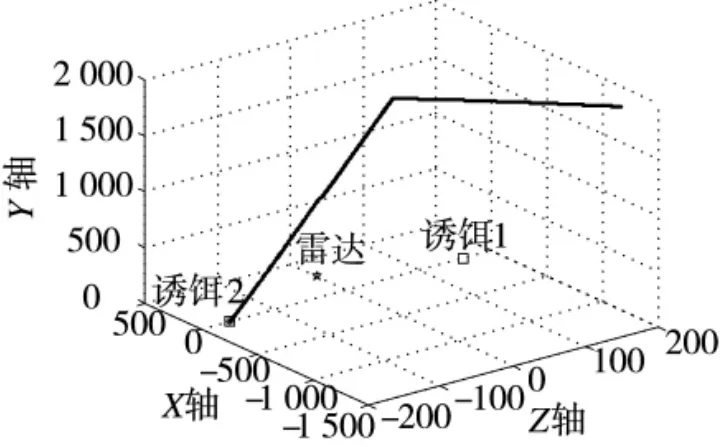
图7 有算法的ARUAV 末制导攻击情况

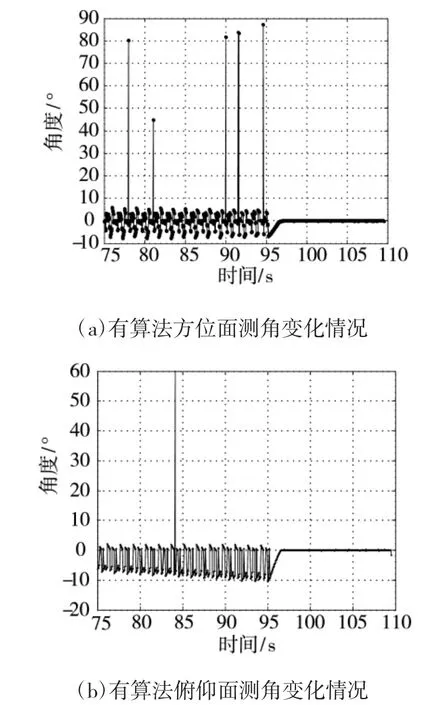
图8 有算法的ARUAV 角度变化情况

由图5 可见，攻击路径粗糙，即使最后有辐射源脱离了ARUAV 的视场范围，ARUAV 也因无法及时机动，最终无法造成有效毁伤。由图6 可见：ARUAV 测角变化较为凌乱，没有明显的规律性、存在较大的异常值，且接收到的不完全重合脉冲信号使导引头测得的跳变角度数据大小也不一样；从数据的不断跳变到归零的变化趋势可以看出，ARUAV飞控系统将按照导引头末制导测角采样周期上传的测向数据适时调整攻击姿态，使ARUAV 始终朝着误差角减小的方向调整，由于导引头天线数据受不完全重合脉冲信号的影响，从而控制机体反复跟踪单辐射源、双辐射源合成信号、三辐射源合成信号。

由图7 可见，ARUAV 在俯冲攻击后，很快锁定跟踪某一辐射源（在本次仿真中为诱饵2），攻击路径平滑，最终ARUAV 落地爆炸点离诱饵2 距离为0.142 8 m，对诱饵2 进行了有效毁伤。由图8 可见：采取本文的算法后，在第97 s 时，即从俯冲攻击开始约2 s 时，算法估算出诱饵2 的位置，结合无源定位与实时匹配位置的方法，使得ARUAV 不再产生反复跟踪不同辐射源的情况；随着ARUAV 的机动调整，测角值在不断减小且几乎为0，说明ARUAV已锁定该辐射源进行跟踪。

3.2 诱饵占空比对算法的影响校验

以3.1 设置参数为例，取ARUAV 的有效毁伤圆概率误差为20 m，用蒙特卡洛的方法重复100 次攻击过程仿真，统计ARUAV 落地点的频数，认为ARUAV 有效毁伤任一辐射源即为有效毁伤系统，ARUAV 应用算法后攻击落点频数分布图如图9 所示。

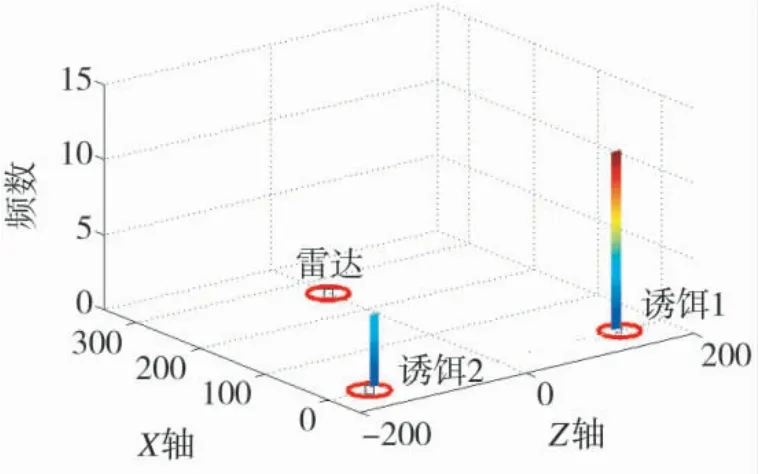
图9 ARUAV 落点分布频数

ARUAV 有效毁伤雷达的次数为0 次、有效毁伤诱饵1 的次数为70 次、有效毁伤诱饵2 的次数为24 次，有效毁伤系统的概率达到了94%，不能百分百有效毁伤系统的原因是存在由噪声引起的测角误差，若去掉测角误差影响，则在该情况下可100%有效毁伤系统。

在影响诱偏效果的参数中，诱饵信号的占空比是一个非常重要的参数，会影响不完全重合信号的信号结构，但现有文献中尚未对占空比进行过相关的讨论。本文取两个诱饵的占空比分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、其余仿真条件与3.1 一致的条件下，用蒙特卡洛的方法重复100 次攻击过程仿真，统计ARUAV 有效毁伤系统的概率，结果如表1、表2 所示。

从表1 可见，没有应用算法时，在大部分两诱饵占空比比例下，ARUAV 都无法有效毁伤系统；在两诱饵占空比相差较大的情况下，ARUAV 对系统有一定的毁伤概率，即表格中数据矩阵的反对角线所连两个对角上存在不为0 的毁伤系统概率，其中，诱饵1 的大占空比与诱饵2 的小占空比条件下得到“上三角”毁伤值，诱饵2 的大占空比与诱饵1的小占空比条件下得到“下三角”毁伤值，且上三角上的毁伤系统概率皆为毁伤诱饵1 的概率，下三角上的毁伤系统概率皆为毁伤诱饵2 的概率，如图10所示，原因在于占空比较小的诱饵信号持续时间短，被导引头捕捉到的概率小，而占空比较大的诱饵信号持续时间长，被导引头捕捉到的概率大，因此，被毁伤的概率更大；在任何占空比比例下，毁伤系统概率皆为毁伤诱饵的概率，即ARUAV 无法毁伤雷达。

表1 无算法情况下ARUAV 有效毁伤系统的概率

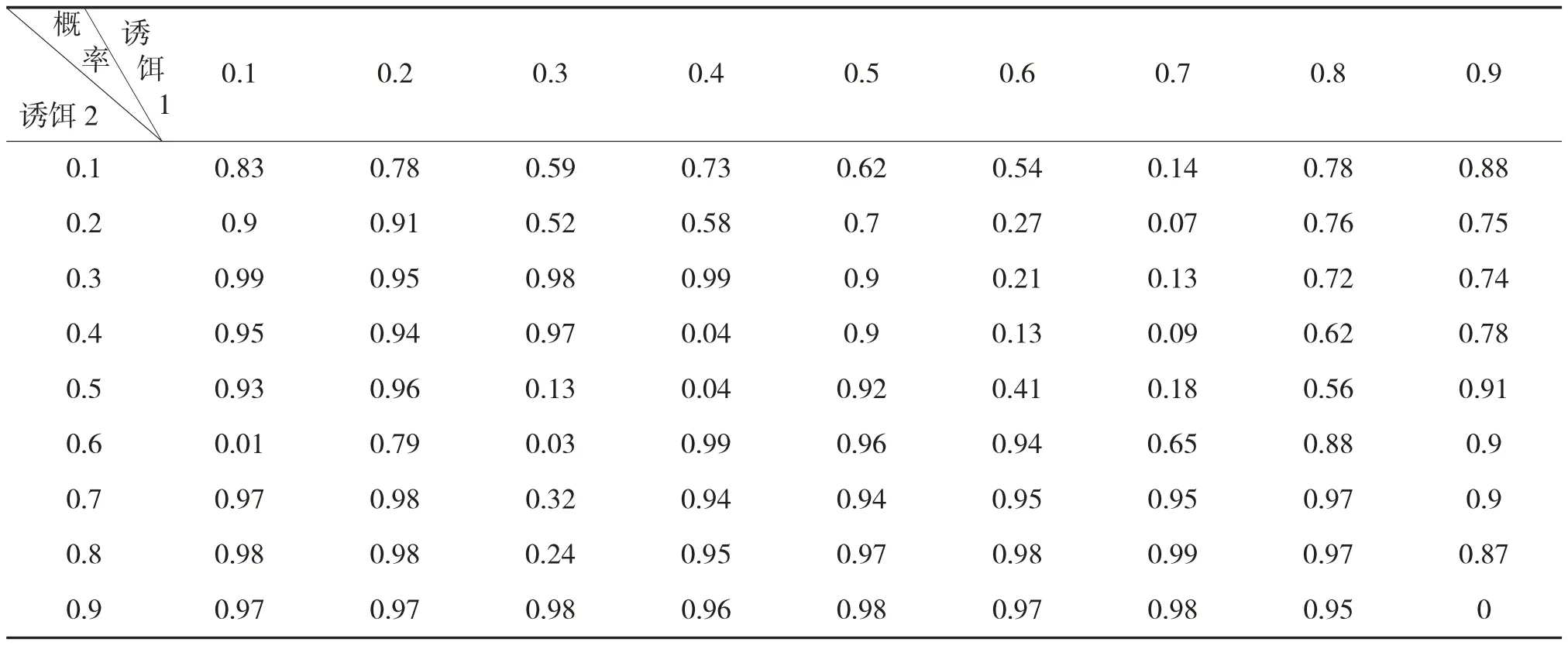
表2 有算法情况下ARUAV 有效毁伤系统的概率

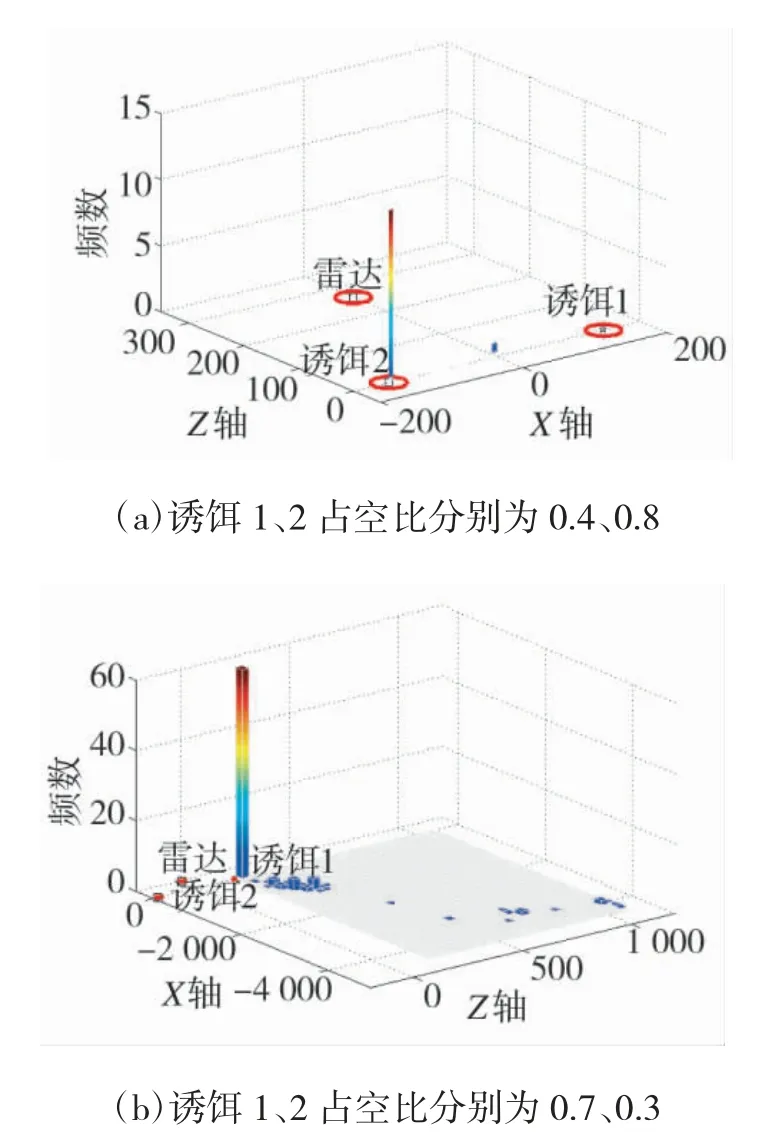
图10 不同占空比下ARUAV 落点分布频数

从表2 可见，应用算法后，在大部分占空比比例下，ARUAV 都可有效毁伤系统；在少数占空比比例下，应用算法后ARUAV 毁伤系统概率低于无算法的毁伤概率。原因在于，算法中一开始确定的被估计值对应的辐射源与信号持续时间长的诱饵不是同一个辐射源，在ARUAV 末制导阶段，ARUAV反而因为两值不同而控制机体反复跟踪两个辐射源，使得最终无法有效毁伤任一辐射源；其次，在少数占空比比例下，毁伤系统概率较低。原因在于，灰色理论要求数据样本中的数据数目不得低于3 个，导引头接收到单诱饵信号的时刻较少，达不到算法要求的数据量，使得ARUAV 被持续诱偏，最终由于机动能力限制无法及时调整，造成无法有效毁伤任一辐射源。

除占空比影响ARUAV 对两个诱饵的毁伤概率以外，诱饵信号的脉冲重复周期、雷达信号的脉冲重复周期、ARUAV 的测向传输周期以及ARUAV 的入侵角度也会对毁伤概率造成一定影响，由于篇幅限制，本文暂不讨论。

4 结论

本文首先分析了异步闪烁诱饵诱偏ARUAV 的原理与不完全重合信号的幅度特性；提出了一种通过实时匹配位置信息来对抗配异步闪烁诱饵雷达系统的方法；最后，进行MATLAB 仿真分析了该算法的有效性及两个诱饵信号的不同占空比对该算法的影响。仿真结果表明，在一定的诱饵信号占空比条件下，本文所提出的方法可以有效对抗异步闪烁诱饵，为ARUAV 抗诱饵诱偏提供了一种新方法。