模糊切换分布参数系统的非脆弱控制器设计

付 俊，刘俊辉，朱阳陈

（1.洛阳铁路信息工程学校，河南 洛阳 471023；2.河南科技大学信息工程学院，河南 洛阳 471023）

0 引言

自从关于T-S 模糊模型的文章发表以来，大量的国内外学者都开始涉及此方向的研究，原因是它在处理非线性系统问题上是一个非常有效的工具［1］。因此，模糊系统到目前为止仍然吸引着许多研究人员的广泛研究［2-5］，通过构建李雅普诺夫函数得到稳定性条件所需要的线性矩阵不等式［6］，基于并行分布补偿控制理论提出更宽松的稳定性条件［7］。值得注意的是，以上所提到的理论都是通过把分布参数系统近似成集中参数系统来处理，这种近似方法就使得系统的控制性能受到限制。在实际的应用过程中，例如研究一个有质量分布的弹性飞行器的运动轨迹时，可以把它看作集中参数系统，即质量集中于质心而不必分析其内部每一点的运动轨迹，但针对弹性振动进行研究时，就需要逐点进行考虑，这就是分布参数系统。许多化工、热工、航空航天和生物控制等工程均是分布参数系统控制研究的领域［8-11］，即采用偏微分方程建模。因此，基于偏微分方程的分布参数系统研究变得极为重要，同时也增加了控制器的设计难度。文献［12］利用模糊控制和Galerkin 理论相结合的方法，对时滞分布参数系统的模糊观测器进行了研究，最后通过线性矩阵不等式的形式得到了稳定性条件。文献［13］针对一类带有马尔科夫跳变的分布参数系统，研究了具有事件触发的滤波器设计问题。然而对带有时滞的非线性切换分布参数系统的模糊控制却没有被考虑。

在过去的几十年里，切换系统在很多的实际系统中得到了很大程度上的应用［14］。切换系统是指由多个子系统和作用在其中的切换规则组成的一类系统，其稳定性不但与系统的子系统是否稳定有关，还与作用在其中的切换规则有着重要关系。就构建切换信号这方面而言，大部分已有文献是采用依赖状态和依赖时间的切换信号，文献［15］对离散脉冲带有时滞的切换系统提出了平均停留时间的方法，文献［16］中基于状态的切换规律，研究了一类非线性参数切换系统的全局自适应有限时间的稳定问题，但是本文考虑的切换信号是任意的。

经过以上讨论，在前人研究的基础上，本文进一步研究了一类带有时滞模糊切换分布参数系统的控制器设计问题。运用T-S 模糊模型描述非线性系统，基于非脆弱控制和PDC 控制理论，设计了比例空间微分模糊控制器。并且考虑了耗散性能指标，使得系统具有较好的抗干扰性能，以矩阵不等式的形式给出了控制器设计方法。最后通过对实际例子的仿真举例验证了所提方法的可行性和准确性。

1 问题描述

本文考虑一类具有时间延迟的半线性抛物型分布参数系统，其描述如下：

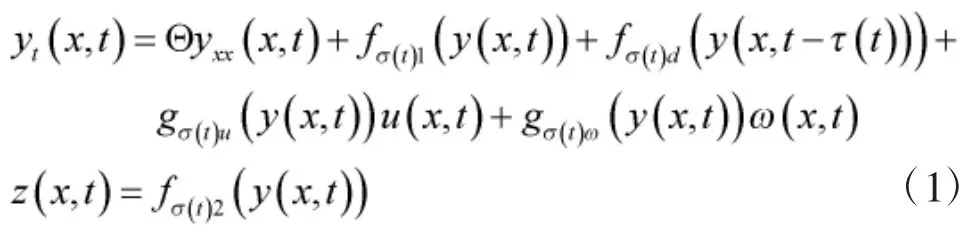
其边界条件和初始条件分别为

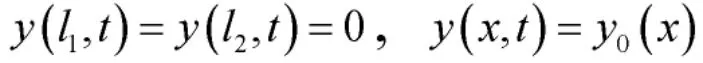
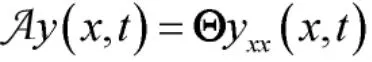
考虑使用下面一类连续时间T-S 模糊系统来描述式（1），其第i 条模糊规则表示为：

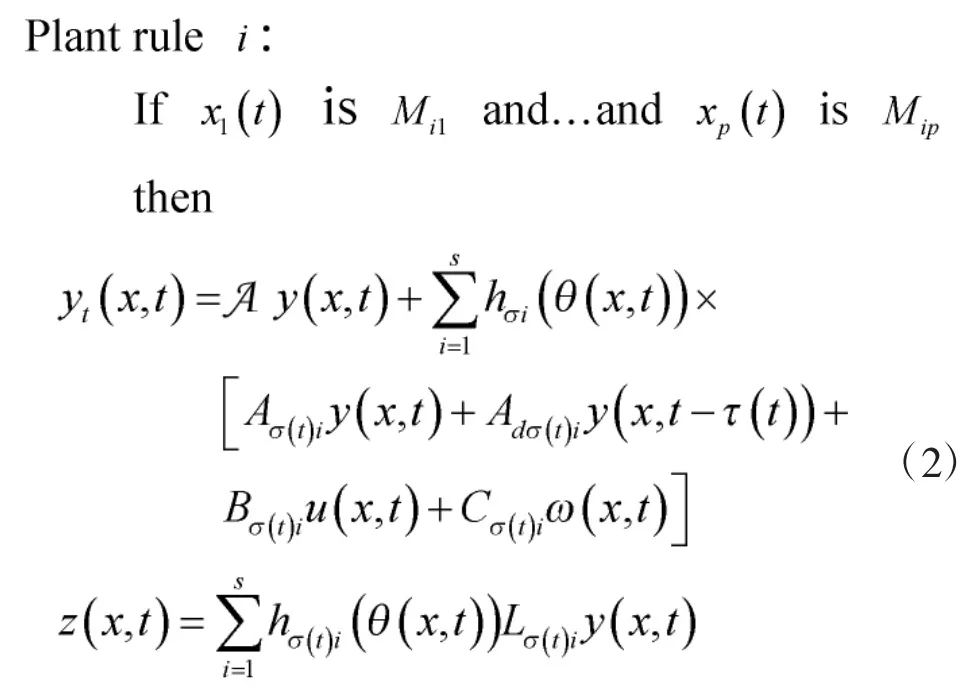
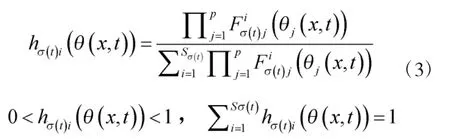
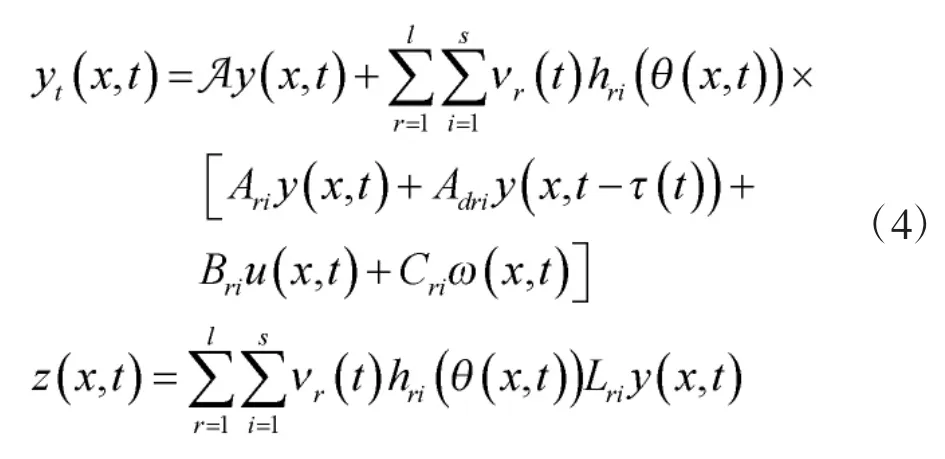
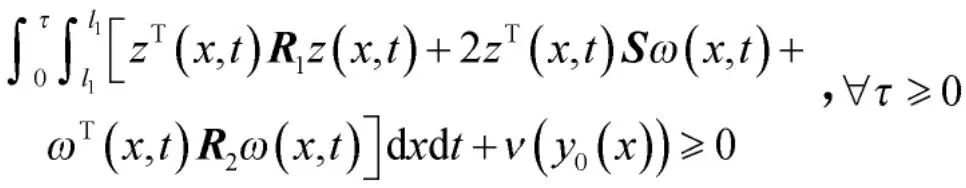
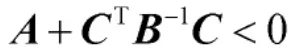
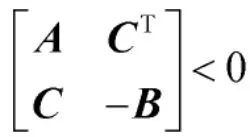
或者

引理2［18］：给出常矩阵X 和Y，对于任意的ε＞0，下面不等式成立：

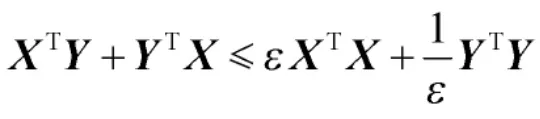
2 控制器设计与稳定性分析

基于T-S 模糊模型和并行分配补偿（PDC）理论，设计如下的模糊控制器

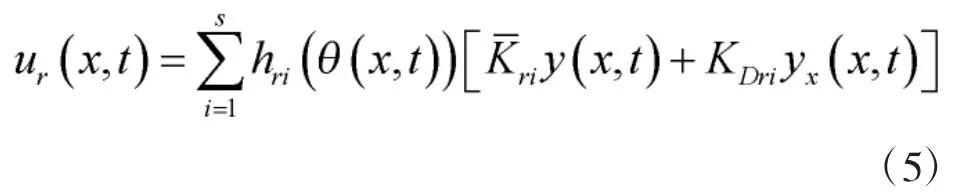
根据系统式（4）和控制器式（5）可得组成的闭环模糊控制系统为

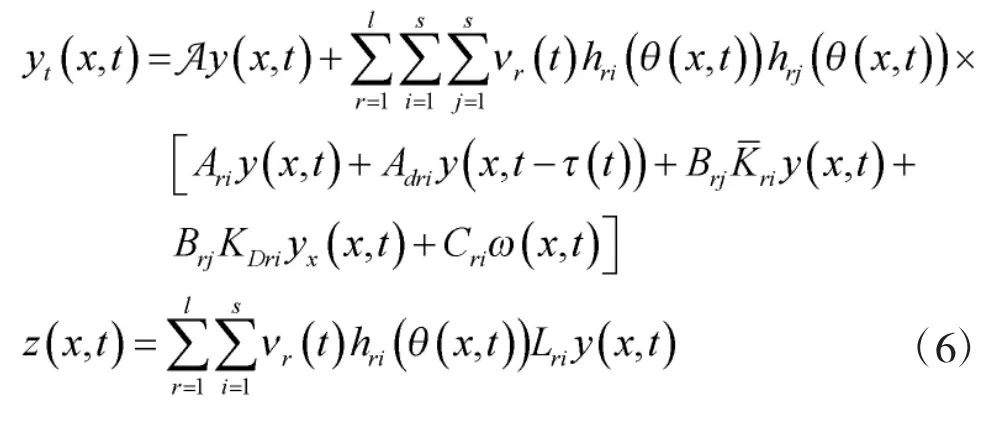
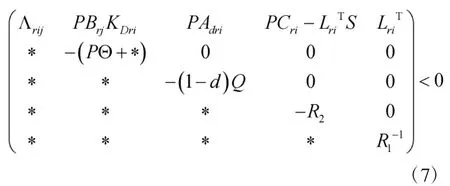
式中

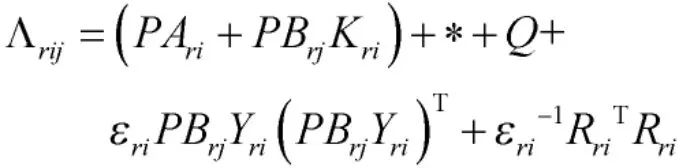
那么对于任意的切换信号都可以使得控制器式（5）保证系统是渐进稳定且满足耗散性能。

证明：选择如下的Lyapunov 函数

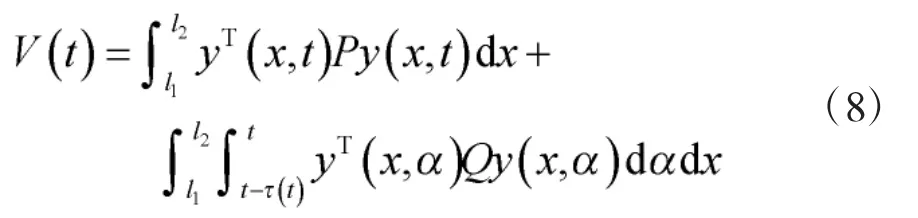
对上述Lyapunov 函数进行求导，可得

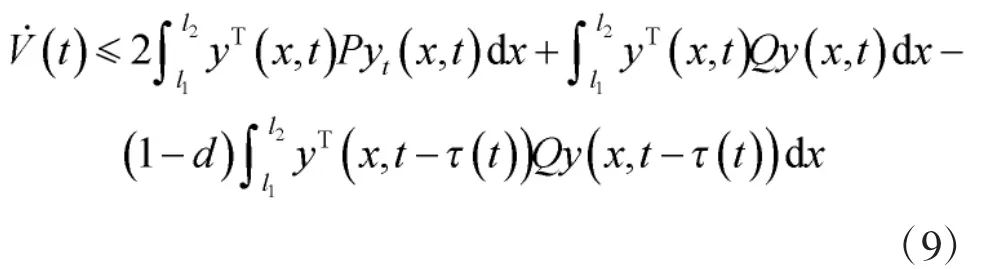
结合闭环模糊控制系统式（6）和系统式（9）可得：

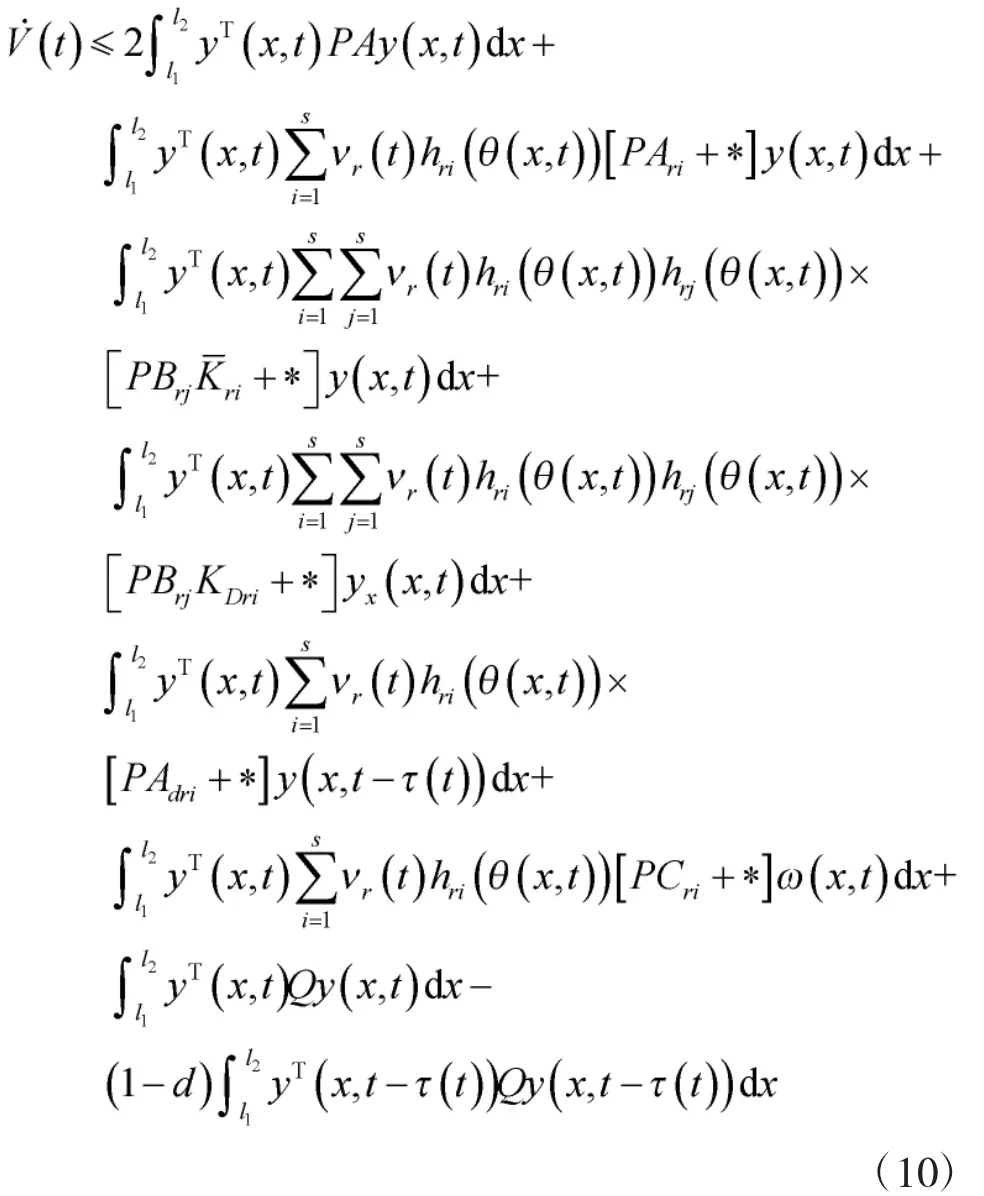
为了求出连续偏导和边界处的解使得系统处于稳定状态，利用格林公式和狄利克雷边界条件可得：

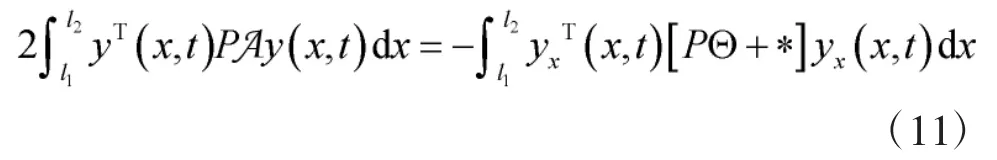
根据引理2 可得

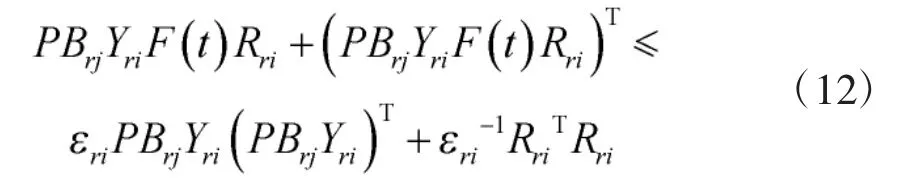
基于式（10）～式（12），可得

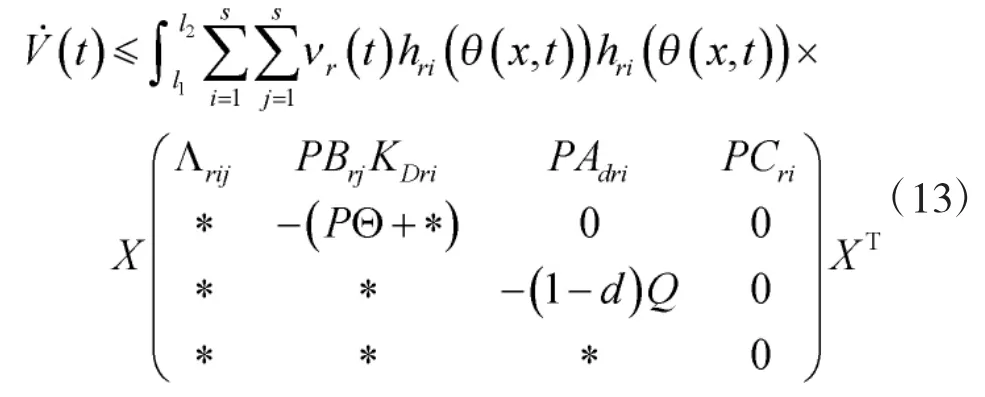
其中，

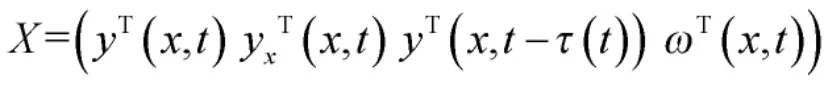
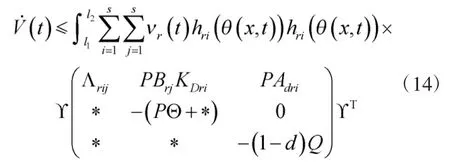
因此，结合不等式（7）和式（14），并根据Lyapunov 稳定性理论可得模糊切换分布参数系统式（6）是渐进稳定的。

同时，根据定理1，可得

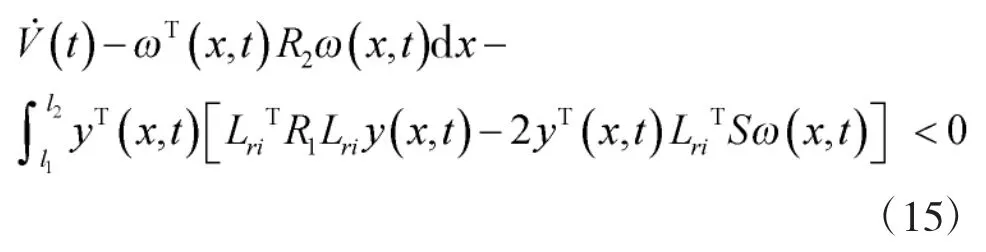
不等式（15）等价于

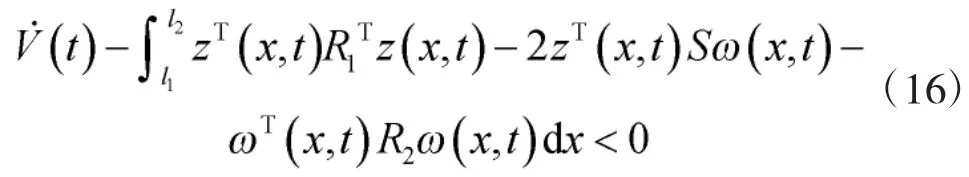
此处假设系统的初始状态为零初始条件，对不等式（16）在［0，］进行积分可得

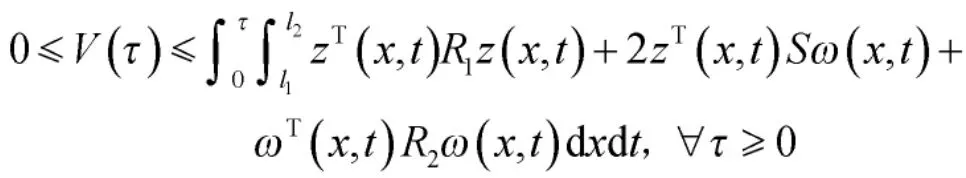
因此，可得到闭环系统式（6）满足耗散性能指标。证明结束。

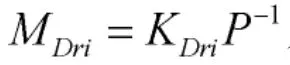
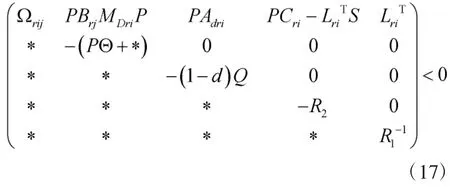
式中

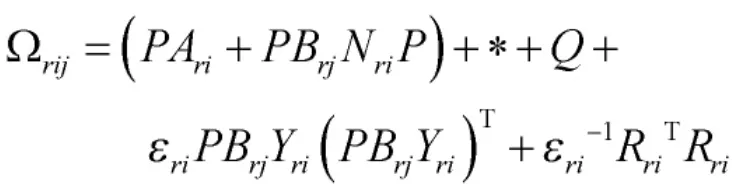
式中

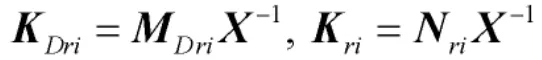
可得到控制器增益。

3 仿真

根据一类反应扩散过程，首先考虑如下模糊切换系统：

针对如下边界条件和初始条件

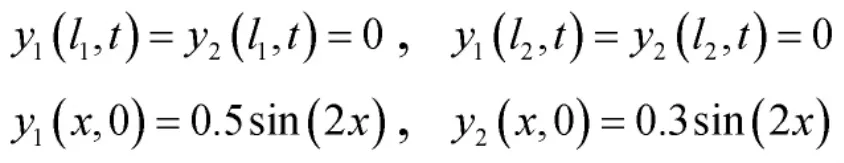
其中

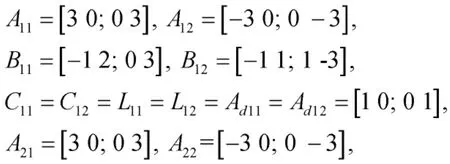
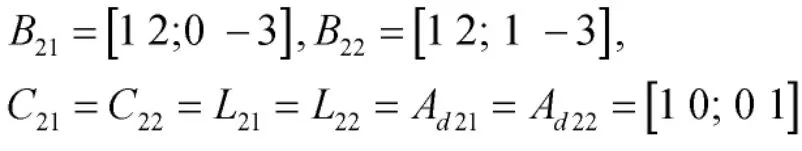
选择系统隶属函数如下：

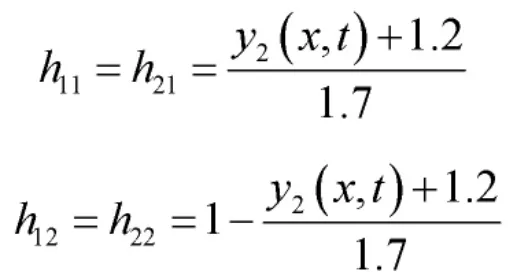
最后，假定

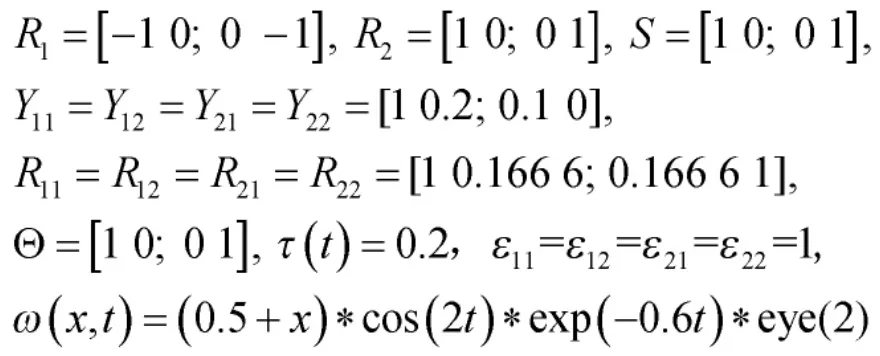
解不等式（19）可得

和微分项增益

仿真如下，图1 和图2 分别为y1（x，t）和y2（x，t）的状态轨迹仿真图，图3 为‖y1（x，t）‖1和‖y2（x，t）‖2的轨迹仿真图，图4 为切换信号。如图1～图3 所示。

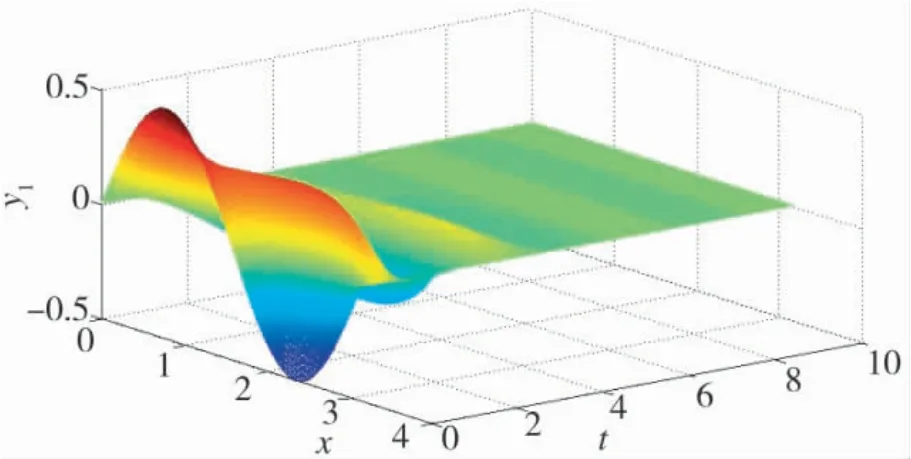
图1 y1（x，t）的轨迹

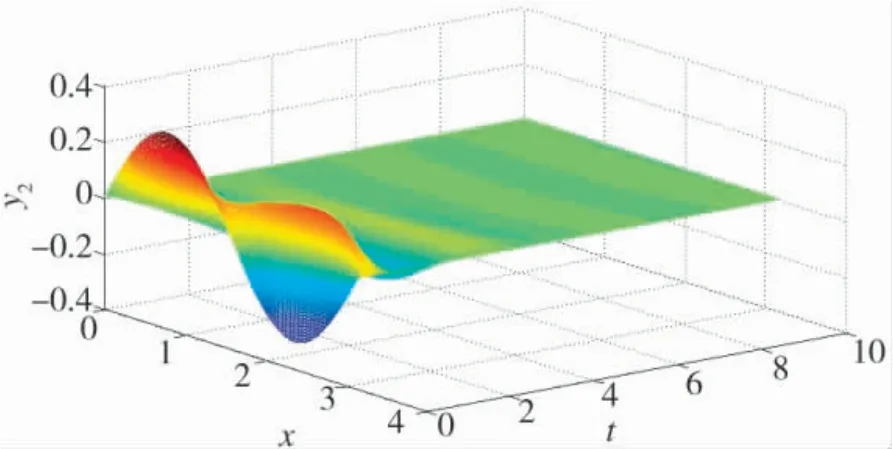
图2 y2（x，t）的轨迹

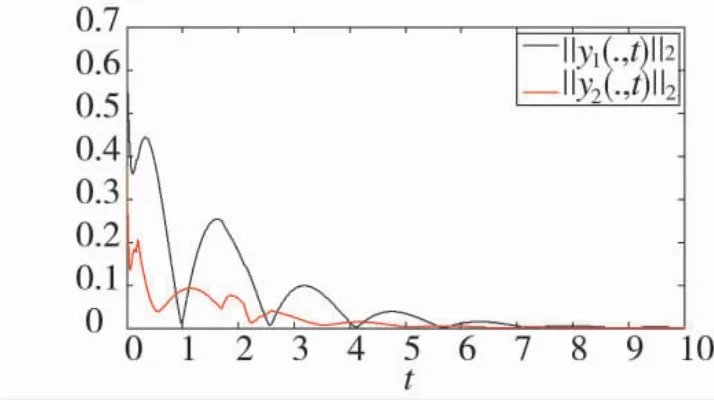
图3 ‖y1（x，t）‖2和‖y2（x，t）‖2的轨迹

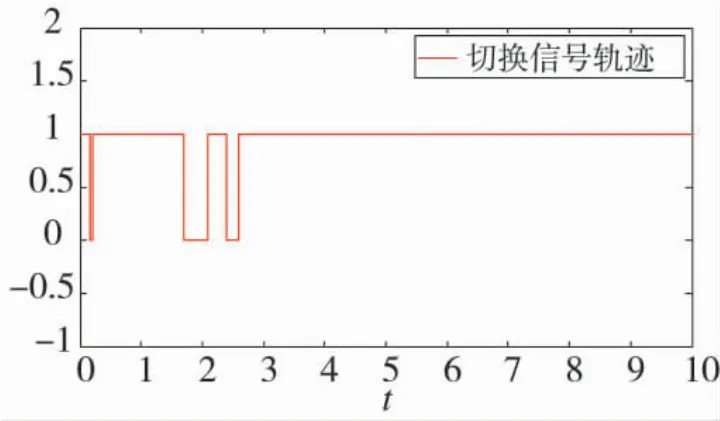
图4 切换信号的轨迹

4 结论

针对带有时滞非线性切换分布参数系统，本文提出了一种有效的控制器设计方法。通过应用T-S模糊模型和PDC 控制理论，结合非脆弱控制技术，设计了模糊比例-空间微分（P-sD）控制器。以线性矩阵不等式的形式给出系统镇定的充分条件，可以很容易得到控制器增益。并且在设计中考虑了耗散性能指标。最后通过MATLAB 仿真验证了控制器设计方法的有效性。