让思考更“进”一步

程利青

摘要：探索活动是学生探索规律、积累数学活动经验的过程。教学中，教师要把新旧知识有机整合，练中有变，变中有比，比中求深，层层递进;促使学生不断超越具体知识和技能，深入到思维的层面，由具体的数学方法和策略过渡到一般性的思维策略，促进学生思维品质的提升，使其养成有根据、有条理、有深度的思考习惯。

关键词：数学活动经验  思维方式  思考习惯

北师大版《数学》六年级下册第一单元实践活动课内容为：准备六张长16 cm、宽4 cm的长方形纸。做一做，想一想。

（1）取出2张长方形纸，一张横着卷、另一张竖着卷，卷成的圆柱形体积一样大吗？猜一猜，算一算。（保留2位小数）

（2）再取出2张长方形纸，照样子做一做。

……

“用6张完全一样的长方形纸卷成不同圆柱”的实践活动，探索“在圆柱侧面积相等时，卷成的圆柱体积相不相等及其缘由”。教师通过把准火候的三次追问，引领学生层层递进，不断走向思维的更深处。

一、“进”，符号表示

问题一“卷成的两个圆柱体积一样大吗”学生直接判断有困难，计算比较势在必行。

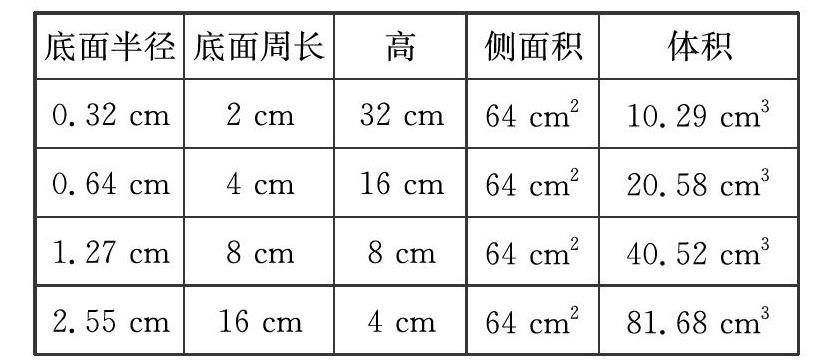
为了凸显计算结果的价值，采取填表的汇报形式（保留2位小数）。

借助表格，学生很快发现：圆柱侧面积相等时，底面积大的体积较大。

教师及时跟进：有更简单的计算办法吗？

学生提出：“除以3.14和乘以3.14算起来很麻烦，直接带着π计算试试。”

如果底面周长是16 cm，高是4 cm。

组1：围成圆柱的底面半径表示为：16÷2÷π=8π，

组2：底面积可以为：8π2×π=64π，

组3：圆柱体积就是：64π×4=256π。

如果底面周长是4，高是16……

学生很快得出，围成的圆柱体积是64π，256π>64π，结论不变。

华应龙强调：学生在同一层面徘徊时，教师要及时跟进，巧妙提升。学生通过观察产生初步的猜想后，教师适时地向前引一引：“有更简单的计算办法吗？”这样既优化了计算的过程，又为学生探索问题二做好了铺垫。

二、“进”，有序排列

问题二既是对初步发现的规律的验证，又是在此基础上更深入的探索。

先请学生判断围成圆柱体积的大小，再计算验证。

学生汇报计算结果时顺序混乱，不便比较。

教师适时跟进：怎样填写，大家研究起来更方便些？

学生观察后提出，可以按从小到大或从大到小的顺序填写。

汇总数据用表格呈现如下，翔实的数据验证了猜想的正确性。

教师再次跟进：这两张粘好的纸条，还能围成别的圆柱形吗？闭上眼睛想一想，如果能，怎样围成的圆柱体积最大？

生1：可以换个方向围。

生2：第二张纸条换个方向，还是一样，因为它是正方形。

生3：如果换个方向围，第一张长纸条围成的圆柱体积大。

学生再次计算填表。（表略）

教師此次跟进，与教科书上的要求不同，引领学生走进了更广阔的思维空间。学生不仅再次经历验证自己猜想的过程，而且经历从动手操作到空间想象的过程，积累了丰富的数学活动经验。

三、“进”，抽象规律

部分同学坚持要展现另一种填表方式。（题目要求保留2位小数，他们的成果没有机会展示）

如果带着“π”计算，确实要简便得多，这是笔者当时的真实想法。

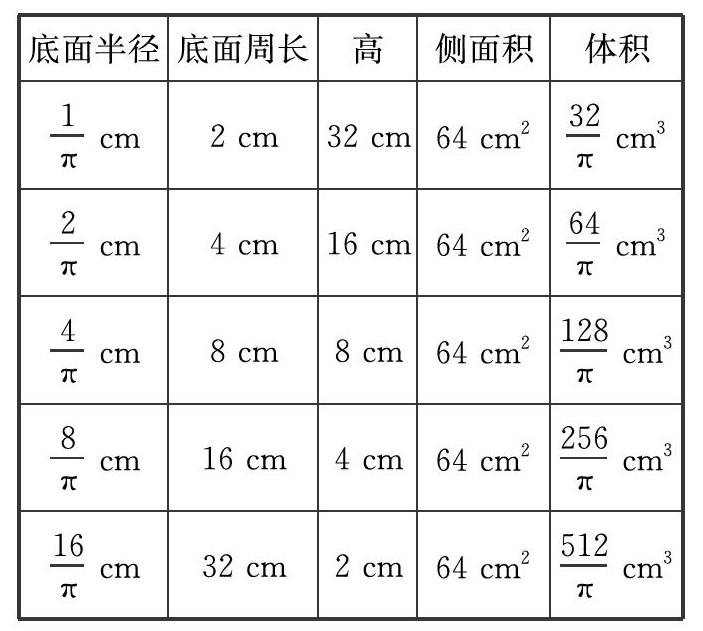
此表一出，全场震惊！

学生不仅发现了“圆柱体的侧面积相等时，底面积大的体积大”，而且还发现了“圆柱的侧面积相等时，底面半径的比=体积的比”。

教师继续追问：是不是所有的侧面积相等的圆柱体，都具有这个规律呢？学生陷入深思。

组1：用字母可以表示运算律，也可以表示这个规律吧。

组2：用a、b表示长方形的长和宽（b

……

于是，同学们的新表又产生了。

学生强烈的探索欲望促使教师又进一步追问：“侧面积相等的圆柱体，底面半径的比=体积的比”具有普遍性吗？感兴趣的同学课后可以试一试……

课后反思：

一、培养学生深度思考的习惯

1.“进一步”促思考

无论是对计算结果的有序排列，还是带着“π”参与计算，以及用字母表示发现的规律，每一个环节教师都有意识地引导学生“进”一步，促使学生深度思考。每一次“进”，都把握火候，找准节点，既立足学生的知识基础，又沟通新旧知识间的联系，不让学生在旧知处徘徊，促使探索活动由课内延伸到课外。

2.“进一步”养习惯

学会思考才有发展潜力。实践活动课不是计算练习课，要引领学生摆脱怕思考、不思考、浅思考的陋习，养成爱思考、真思考、深思考的思维习惯。恰如郑毓信所言，“通过数学学会思维”。波利亚也指出，“知识和能力的核心是思维”。数学学习不仅要获得知识、提高能力，更要促进思维品质的发展，养成有根据、有条理、有深度的思考习惯。

二、培养学生深度思考的策略

1.培养学生勇于探索的精神

实践活动课的学习氛围，让多数学生不知不觉地参与进探索活动中。他们动脑想、动嘴说、动手测量和计算，对结果有了初步的猜想并用计算数据验证发现，再通过集体的多次实验得出正确的结果。在活动过程中，学生合作需求强烈，探索欲望“爆棚”，理性思维、批判质疑的火花不断闪现，探索精神得到充分张扬。

2.培养学生深度探索的习惯

六年级的学生对探索规律的常用策略并不陌生，他们经历了运算律、图形面积和体积公式推导等的探索过程，积累了较为丰富的数学活动经验。他们能依据教材提供的问题情境寻找有用信息，经历从不同算式得到相同规律的过程，再通过举例验证、比较分析，完善对规律的认识。学生带着“π”计算，为用字母表示规律做好了铺垫，从具体的数据中跳出来，由特殊到一般，关注事物的本质属性。养成用科学的思维方式认识事物、解决问题的习惯，数学的核心素养才能得到可持续发展。

参考文献：

[1]林崇德《中国学生发展核心素养到思维品质的培养》（讲座）

[2]余文森.核心素养导向的课堂教学[M].上海：上海教育出版社，2019.

[3]北师大版六年级数学下册教科书，2014.