基于分段线性回归的煤机装备机载操作臂定位误差补偿方法

贾运红，王振翀，焦晓峰

1.中国矿业大学(北京)机电与信息工程学院，北京 100083；2.中国煤炭科工集团太原研究院有限公司，山西太原 030006

随着科学技术的发展进步，实现煤机装备机载操作臂的自动化作业控制已成为当前研究的热点问题。在操作臂自动控制系统中，定位精度是衡量系统性能的关键性指标。一直以来，巷道围岩的控制与支护都是煤矿巷道掘进过程中备受关注的问题[1]。锚杆转载机、掘锚一体机等支护类煤机装备的操作臂存在自动定位误差补偿问题；此外，综合掘进机、转载破碎机、连续采煤机等采掘类煤机装备的自动定位精度校准问题也日益凸显。煤机装备操作臂若定位精度过低，可能会造成碰撞、挤压、网片损坏、人员伤害等安全隐患。笔者以一种应用于煤机装备的典型机载多关节操作臂为对象进行误差补偿研究。此操作臂能够实现自动伸缩、俯仰、偏转、旋转等动作，但由于煤机装备机载多关节操作臂存在制造误差、装配误差、编码器的安装误差，以及操作臂变形、工作温度变化等引起的误差，这都对煤机装备操作臂的定位精度造成影响。

随着机器人技术的发展和煤矿高效生产的需求越来越多，不同结构的机器人逐步应用在煤矿行业中[2]。目前，针对煤机装备操作臂位置误差补偿的研究较少，而基于机器人位姿误差补偿的研究较多，大多数都是基于模型进行补偿。基于模型的运动学补偿流程主要包含：误差建模、误差测量、参数辨识以及误差补偿4部分[3-4]。如夏毅敏等[5]以DH法建立臂架正运动学模型，通过计算臂架动态误差和静态误差，建立运动学误差补偿模型，并采用多种群遗传算法求逆解实现钎杆定位；He等[6]提出了基于POE模型的机器人补偿方法；徐昌军[7]采用5自由度的MDH建模，基于微分变换进行误差补偿；Filion 等[8]利用模型对机器人进行补偿，并利用MaxSHOT 3D仪器对模型补偿进行校准；刘常杰等[9]以DH模型为基础，利用视觉传感器测量出坐标，根据固定点坐标与机器人参数的关系，反向求解出机器人变化的参数，实现机器人模型参数实时补偿；陈钢等[10]针对机器宇航员提出了一种基于MCPC(修正的完整参数连续)模型的运动学参数标定方法；Stone[11]提出了一种 S 模型。上述研究是通过基于模型的方法进行误差补偿的，存在误差模型建立复杂、计算困难等问题。

由于神经网络具有适用性广、精度高等优点，人工神经网络的方法已用来进行误差补偿和校准[12-14]。Nguyen 等[12]将卡尔曼滤波算法和人工神经网络相结合增强机器人的精度，但神经网络具有训练时间长、调节参数困难等问题。Yuan等[15]利用ELM极限学习机算法提高了绝对定位精度；戴厚德等[16]基于ELM极限学习机提出了基于再生权最小二乘法的最优剪枝极限学习机算法，解决了建模和计算复杂等问题，该方法相对神经网络来说计算效率大大提高，但需要价格昂贵的测量设备，测量成本高。刘鹏坤和王聪[17]将机器视觉技术应用于煤矿井下的测量，降低了测量成本，但是视觉测量技术防护困难，操作复杂。陈慎金等[18]设计了一种自整平式仪器平台，实现了全站仪自动整平，保证了测量过程的自动化，但全站仪只能进行静态测量与补偿，不利于在线补偿。

本文针对一种应用于煤机装备的典型机载多关节操作臂结构开展研究，并进行正运动学模型和逆运动学模型的建模，结合分段线性回归算法[19]提出了一种简单有效的定位补偿方法。经过实验验证，补偿后x、y、z三个方向的均方根误差和平均绝对误差分别降低到100 mm以下，重点关注的3个定位点3个方向的绝对误差均降低到100 mm以下，补偿后的精度满足误差在100 mm以下的工业需求。

1 运动学模型

1.1 多关节操作臂

图1是一种应用于煤机装备的典型机载多关节操作臂示意图。共有6个自由度，包括转动自由度θ1、θ2、θ4、θ5、θ6，定义为绕对应坐标系的z1、z2、z4、z5、z6轴旋转；移动自由度d3，沿坐标系S3的z3轴伸缩。各关节坐标系S0-S6原点为O0-O6，遵循笛卡尔坐标系原则建立各坐标系[20]。

绕坐标系S6的y6轴转动-90°，并沿着x6、y6、z6轴方向平移一定距离可得定位点坐标系S7，原点为O7。

图1 煤机装备机载多关节操作臂示意图Fig.1 Schematic of airborne multi-joint operating arm of coal machine equipment

1.2 正运动学模型

已知转动关节角度值或移动关节长度值求定位点的空间位姿，即运动学正解运算。

位姿变换矩阵通式为

(1)

坐标系Si+1在坐标系Si中先沿坐标轴xi、yi、zi方向分别平移xi0、yi0、zi0，再绕坐标系Si中的ωi轴旋转θ角形成变换矩阵。其中，平移距离为xi0、yi0、zi0，旋转角度θ的取值以及ωi轴的选取由坐标系Si+1和坐标系Si相对位姿决定。

各坐标系对原点坐标系位姿矩阵为

(2)

由式(1)、式(2)可得定位点的空间位姿矩阵为

(3)

式中，nx、ny、nz、ox、oy、oz、ax、ay、az为定位点坐标系S7各坐标轴与坐标系S0各坐标轴的姿态关系；Px、Py、Pz为定位点原点O7相对S0坐标系的坐标值。

本文主要研究定位点的位置校准。采样点x、y、z方向的坐标值为

Pxi=fx(θi) (i=0～m)

(4)

Pyi=fy(θi) (i=0～m)

(5)

Pzi=fz(θi) (i=0～m)

(6)

θi=[θi1，θi2，di3，θi4，θi5，θi6](i=0～m)

式中，m为采样点数量；Pxi、Pyi、Pzi为5个转动关节角度值和1个移动关节长度值的函数。

1.3 逆运动学模型

已知定位点的空间位姿矩阵，求转动关节角度值或移动关节长度值，即运动学逆解运算。根据式(3)可得

(7)

根据式(7)矩阵两边对应元素相等，列多元方程求解，可求得θ1、θ5、θ6的值[20]，即

(8)

θ5=arcsin(-nxsθ1+nycθ1)

(9)

(10)

同理，求得d3、θ2、θ4的值，即

(11)

(12)

(13)

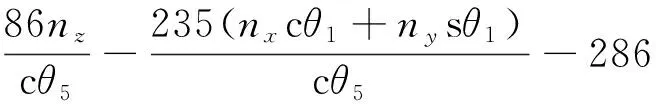
式中，sθ、cθ分别为sinθ、cosθ。

2 误差补偿

2.1 线性回归

线性回归模型为

(14)

θ=[θ0，θ1，…，θn]T，x=[x0，x1，…，xn]T

确定线性回归模型即求得θ。均方误差是回归任务中最常用的性能度量，线性回归的目标函数为

(15)

式中，x(i)为第i个样本；y(i)为第i个理想值。

均方误差最小化过程，称为线性回归模型的最小二乘法参数估计[21]。式(15)向量化后有

(16)

式(16)偏导为0可使误差最小，则有

θ=(XTX)-1XTY

(17)

2.2 测量数据

在操作臂每个旋转关节处安装角度编码器，分辨率12位，即编码器能够识别的最小角度为0.088°；在操作臂可伸缩关节处安装位移传感器，输出信号为4 ～20 mA，可测得位置点i的5个关节角度和1个伸缩长度。

2.3 误差补偿原理

2.4 分段线性回归

通过提取多关节操作臂的周期性变换特征，建立了z方向的误差模型。在一个自动定位过程中，操作臂摆到巷道最边上目标位置的垂直下方，从这个位置开始采集数据，如图2所示。z方向的时间序列曲线主要包括：操作臂先上升，开始定位第1个点，完成支护后，开始下降，下降到位后向内侧平移一定距离；又开始上升，上升到位后定位第2个点，完成支护开始下降，下降到位后向内侧平移一定距离；又开始上升，上升到位后定位第3个点，完成支护后开始下降，一个工作周期完成后，再移动到操作臂的初始位置。操作臂上升、下降、平移时负载差距较大，误差规律也有区别，因此要建立分段线性回归模型进行误差分析。

图2 z方向目标路径曲线Fig.2 Target path curve in z-direction

一般情况，分段线性回归使用指示变量对不同范围的数据拟合统一的回归模型，有一个转折点的线性回归模型[19]为

E(Yt)=β0+β1Xt+β2(Xt-Xt0)Dt

式中，Dt为指示变量。

指示变量分段线性回归可以转换为多元线性回归求参数问题。对于本系统来说，需要求得测量值与目标值之间的线性关系，定位点是中断点，很难转换为多元线性回归问题。因此，将采集的数据重新整理，分为3组集合Up、Down、Parallel，分别进行线性回归处理。

Up={Pzi|i∈[0，3]∪[14，17]∪[28，31]}

Down={Pzi|i∈[4，6]∪[18，20]∪[32，34]}

Parallel={Pzi|i∈[7，13]∪[21，27]}

2.5 目标值补偿

煤机装备的多关节操作臂实际运行时，以x方向补偿进行说明。测量数据是操作臂实际运行到的位置点，根据采集的测量数据和目标数据进行线性回归拟合，由式(17)得线性回归参数θ0、θ1，由式(14)得测量值与目标值线性回归曲线模型为

Pmx=θ0+θ1Pcx

(18)

若让操作臂实际运行到目标位置，则根据线性回归曲线模型对目标值进行修正，将目标值作为测量值代入式(18)有

(19)

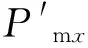
当设备以“修正目标”为目标运行时，按照预测分析，实际应运行到“目标位置”，完成误差补偿。

3 实验研究

3.1 关节姿态零位标定

6个自由度旋转关节或伸缩关节零位对准精度是定位准确的充分条件。因此，零位标定是多关节操作臂自动运行前的必备工作。

关节臂式三坐标测量机由关节臂、控制电路、上位机软件及附件等组成(图3)。关节臂包括3根刚体臂、3个活动关节和1个测头；处理软件为Polyworks软件，便于携带、组装方便、数据处理迅速、测量精度高。

图3 零位标定系统Fig.3 Zero calibration system

零位标定方法：首先，进行测量准备工作，清理打磨除去测量面的污垢，构建关节臂式三坐标测量系统，测量系统由被测工件、测量机组成；然后，将多关节操作臂作为被测工件，将三坐标测量机三脚架作为基座，关节臂装配在三脚架上，测头装配在末端臂上[22]；分别将操作臂6个自由度调至零位，缓慢平移三脚架，调节测量机与被测工件表面之间的距离，测得Δθi0(i=1，2，4，5，6)，Δd30，根据测量的零位误差，在控制程序中进行角度补偿处理。

3.2 误差判断

用m个位置的均方根误差RMSE和平均绝对误差e对目标值补偿后的运行效果进行综合判断，公式为

式中，xcx为测量值；xmx为目标值。

将x、y、z方向的目标序列修正为“修正目标序列”，多关节操作臂按照此目标运行1个工作周期后进行分析。分析实际运行的测量值与理想目标值均方根误差和平均绝对误差，由此结果判断补偿效果。

3.2.1x、y方向补偿效果

(1)x方向补偿前后误差对比如图4所示。补偿后，均方根误差由109.87 mm下降到48.63 mm；平均绝对误差由101.46 mm下降到 44.06 mm。3个红色圆圈为三个定位点补偿前的误差，3个红色五边形为三个定位点补偿后的误差。

(2)y方向补偿前后误差对比如图5所示。补偿后，均方根误差由97.18 mm下降到 34.09 mm；平均绝对误差由86 mm下降到 28.43 mm。

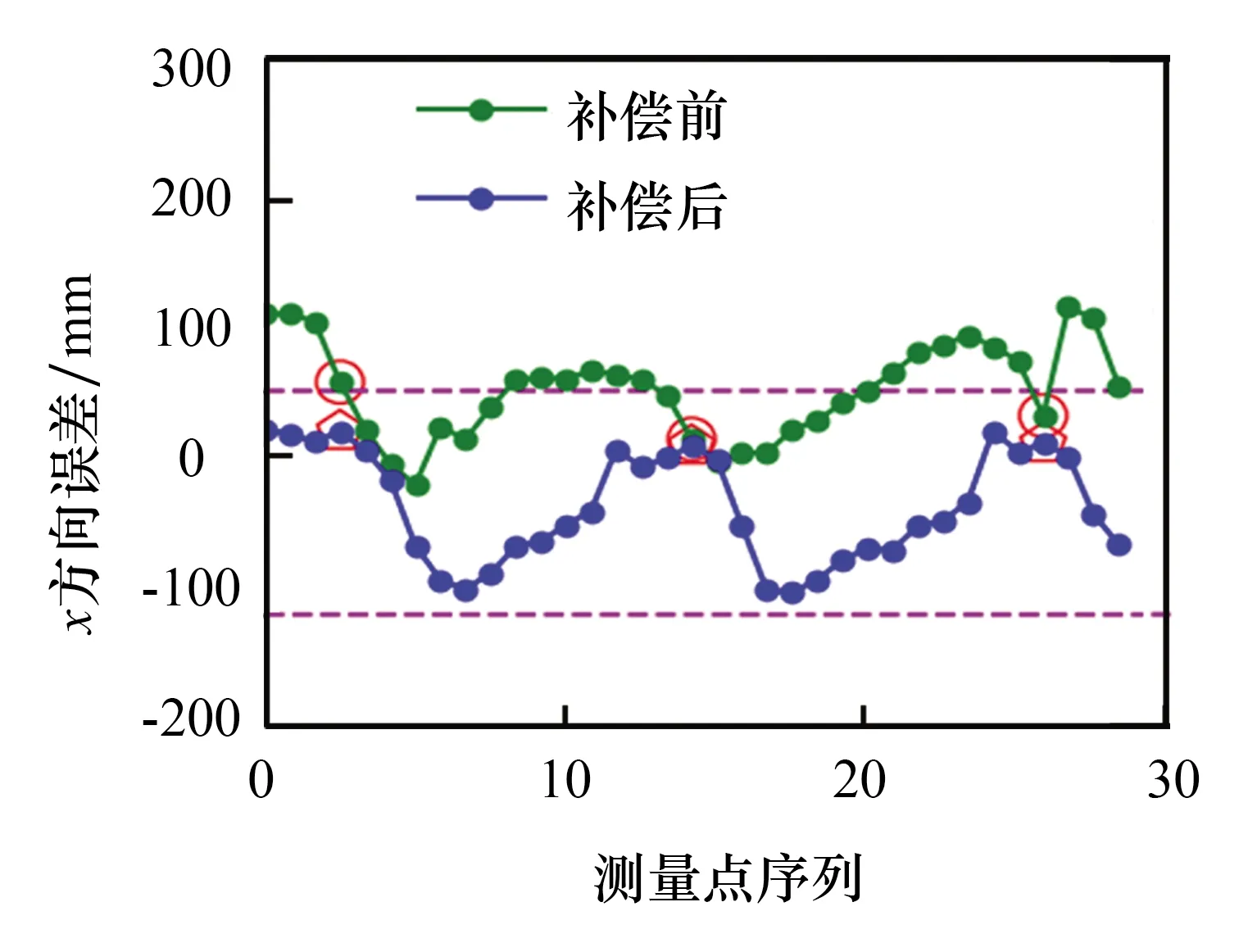
图4 x方向补偿前后对比Fig.4 Contrast figure before and after x-direction compensation

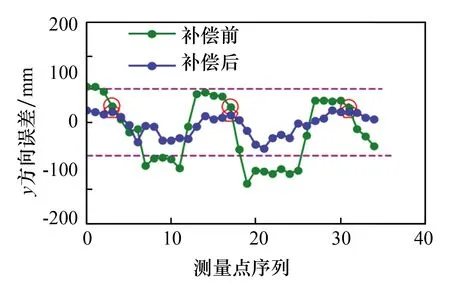
图5 y方向补偿前后对比Fig.5 Contrast figure before and after y-direction compensation

3.2.2z方向补偿效果

在z方向的补偿实验中，对比了整体线性回归与分段线性回归的效果。

当针对样本整体进行线性回归拟合得出拟合曲线，根据拟合曲线修正目标值，运行1个周期得出测量曲线，如图6所示。z方向均方根误差由91.26 mm下降到90.65 mm；平均绝对误差由77.03 mm变化到77.80 mm；上升时补偿效果明显，下降时补偿效果不明显。

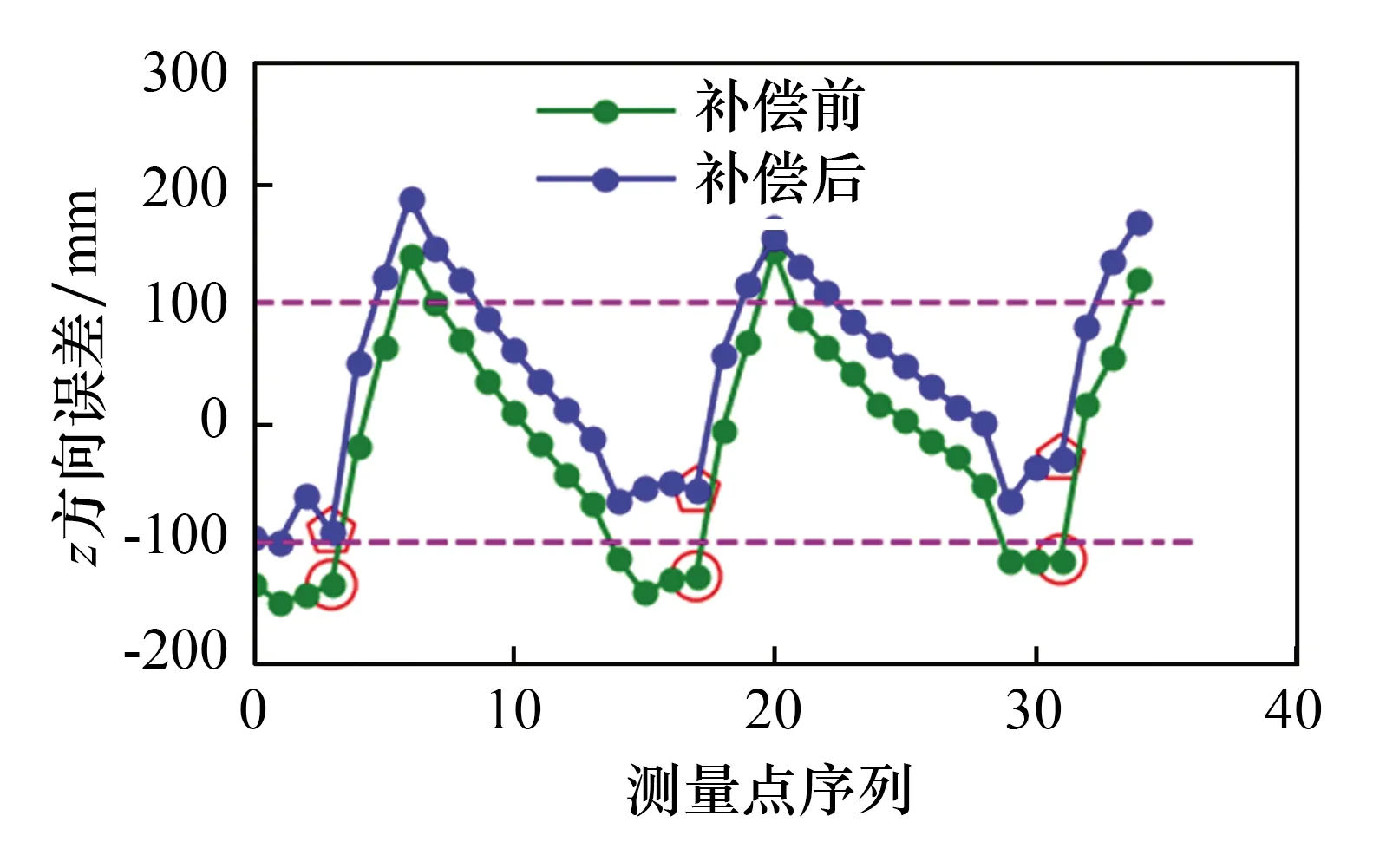
图6 样本整体进行测量值与目标值线性回归拟合Fig.6 Linear regression fitting of measured values and target values for the whole sample

对数据集分段整理，各段分别进行线性拟合得出各段拟合曲线，根据各段拟合曲线分别修正目标值，运行1个周期得出测量曲线，如图7所示。补偿后，z方向均方根误差由91.05 mm下降到 70.19 mm，平均绝对误差由77.54 mm降低到 60.06 mm，整个工作周期补偿效果明显提高。采样点中有几个点的绝对误差大于100 mm，分析后发现这几个点的采样位置振动较大，由于振动引起编码器采样偏差等原因可能造成误差较大。笔者关注的3个定位点补偿后绝对误差由100 mm以上降低到100 mm以下，补偿效果明显。

图7 测量值与目标值分段线性回归拟合Fig.7 Piecewise linear regression fitting of measured values and target values

3.2.3 定位点补偿效果

对路径点的补偿是为了定位更准确，3个定位点[Px，Py，Pz]的绝对误差见表1。由表1可见，经过修正后定位点[Px，Py，Pz]误差均在100 mm以下，满足工作需求。

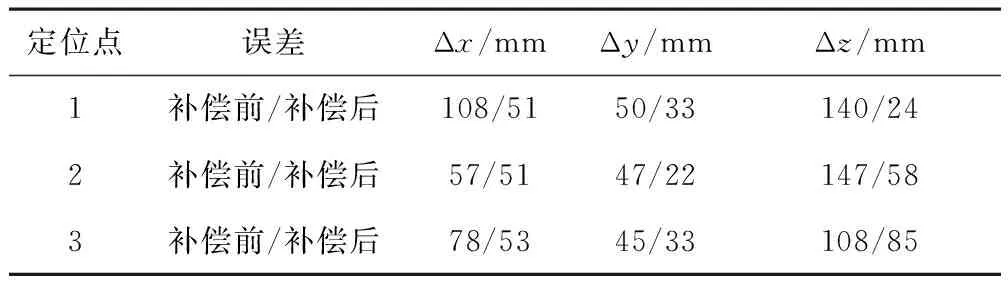
表1 定位点补偿前后绝对误差对比Tab.1 Absolute error comparison of positioning points before and after compensation

4 结 论

(1) 利用煤机装备多关节操作臂上的角度编码器，结合机器学习中的线性回归算法和运动学模型进行多关节操作臂定位误差补偿的研究，实验表明，控制系统依据学习模型建立的“修正目标序列”路径运行，实际到达的位置点和“理想目标序列”的误差明显减小：x、y、z方向的均方根误差分别降低了55.7%、64.9%、22.9%；x、y、z方向的平均绝对误差分别降低了56.6%、66.9%、22.5%。

(2) 定位系统实验中最关注的3个定位点的精度明显提高。多次实验表明，每次补偿后3个定位点x、y、z三个方向的绝对误差均降低到100 mm以下，满足煤矿井下误差要求在100 mm以下的工作需求。

(3) 本文提出的分段线性回归补偿方法减少了测试成本，节省了补偿时间，适用于误差在线补偿，操作简单，实用性强。

(4) 本文提出的分段线性回归补偿方法的定位精度仅适用于误差要求在100 mm以内的需求，后续需要进一步研究适用于更高定位精度的煤机装备多关节操作臂误差补偿方法。