基于BP神经网络PID的液压支架初撑力自适应控制

胡相捧，刘新华，庞义辉，刘万财

1.中国矿业大学(北京)机电与信息工程学院，北京 100083；2.中国矿业大学(北京)智慧矿山与机器人研究院，北京 100083；3.天地科技股份有限公司开采设计事业部，北京 100013；4.中煤新集能源股份有限公司口孜东矿，安徽阜阳 236100

液压支架的承载分为主动(或初撑)增阻、被动(或承载)增阻、溢流恒阻3个阶段。其中，主动增阻阶段的液压支架力称为初撑力，它是支架的重要参数，在对顶板的控制中具有重要作用。保证支架的初撑力不仅能够提高顶板的强度和稳定性，减少顶板离层、端面破碎度和煤壁片帮，还可以提高支护系统的刚度，减少顶、底板相对移近量。不同的顶板条件对初撑力的要求也不一样，为了使支架发挥较高的支撑水平，初撑力与工作阻力的比值宜取60%～85%[1]。刘强等[2]采用数值模拟分析了不同液压支架初撑力对煤壁的影响，得出提高初撑力可有效减小煤壁水平位移和垂直应力。刘闯等[3]分析了液压支架初撑力对顶板的控制作用，得出初撑力与工作阻力的比值为0.65～0.70时，具有最佳效果。与综采工作面的顶板压力实时变化相似，综掘巷道的压力也是实时变化的。薛光辉等[4]提出了确定综掘巷道超前支架最佳支护时机的方法。

液压支架初撑力的控制方式有2种：三位四通手动操纵阀的开环控制和两位三通电磁换向阀的先导控制。采用的控制策略是将检测立柱下腔的实际压力与初撑力设定值进行比较，若立柱下腔压力低于设定值，则电磁换向阀打开供液并持续一定时间，程序一般设定补压3～5次。

为了保证液压支架达到合格的初撑力，在传统控制方法基础上，邱常青[5]通过增加单个支架的升架时间使初撑力达到相对稳定状态。曹连民等[6]设计了一种液压支架初撑力手动增压装置，通过手动控制来提高支架初撑力。何勇等[7]针对巷道底板高低不平，提出了液压支护平台的异步自抗扰平衡控制方法。栾丽君等[8]研究了一种超前支架速度、压力复合控制方法，将模糊滑模变结构算法作为控制策略，提高了支护效率。Cao等[9]将液压支架的推移千斤顶采用位移伺服控制，比较了系统启闭时的阀芯位移和系统流量曲线，说明了伺服控制系统的应用效果。李明等[10]将RBF神经网络引入UMAC的PID参数调节中，增强伺服系统的自适应性和鲁棒性，并提高系统动静态特性。

以上对支架初撑力的控制方法仍然采用人工控制、先导控制和人为干预的方式。电液先导控制是目前液压支架采用的最先进的控制方法，但从现场情况看，现有的方法仍不能有效地实现支架初撑力控制。神经网络作为一种智能的控制方法具有能够逼近任意非线性函数的优点[11]，在煤矿领域多有应用。杨小彬等[12]采用改进的广义回归神经网络对煤矿工作面的低氧问题进行预测。赵红泽等[13]采用GA-BP神经网络模型对拉斗铲生产能力进行了预测。如今，在浅部煤层条件较好的煤矿进行智能化开采已取得了巨大进步，而神经网络控制方法应用于支架方面多是从支架的可靠性、轻量化、姿态监测等角度进行研究[14-16]，并没有应用于支架立柱压力的控制。随着经济的发展，实现在恶劣开采条件或深部煤层的智能化开采势在必行。基于神经网络的人工智能、大数据、自学习等方面的技术已有大量应用。因此，改进现有的支架控制方法，将先进的智能控制方法应用于支架控制将大大推进煤矿智能化开采的进程。

笔者现场跟踪几个配备先进自动化装备的煤矿发现，支架的初撑力合格率很低，经常出现整个工作面初撑力合格率为零的现象，而且初撑力无法快速响应。针对液压支架初撑力难以保证和稳定的问题，建立了立柱电液力控制系统数学模型，提出了基于BP神经网络的PID初撑力自适应控制方法，并建立了三层神经网络控制模型，采用有监督的Hebb学习规则和梯度下降法对输出层和隐含层的权值系数进行更新，经训练得到PID控制器的3个控制参数，通过仿真试验表明该方法的有效性。

1 液压支架初撑力电液力控制系统数学模型

1.1 液压支架立柱控制系统

液压支架由液压缸(立柱、千斤顶)、结构件(顶梁、掩护梁和底座等)、推移装置、控制系统和其他辅助装置组成。立柱是关键的承载油缸之一，用于主动给予顶板压力和被动承载顶板来压。目前液压支架所使用最先进的控制阀——电磁换向阀是一种两位三通先导阀，与立柱下腔的压力传感器构成闭环回路，但反馈给电磁换向阀的信号是开关信号，仅能实现初撑力不足时持续供液，不能控制立柱流量，控制精度低，响应速度慢。控制原理如图1所示。若支架为两柱掩护式架型，图1的10为左右立柱；若支架为四柱支撑掩护式架型，则10为前排立柱的左右立柱，后排立柱原理图同前排立柱。

1—泵箱；2—截止阀；3—过滤器；4—回液断路阀；5—电磁换向阀；6—安全阀；7—压力传感器；8—压力表；9—液控单向阀；10—立柱图1 立柱控制系统Fig.1 Control system of leg

王磊等[17]采用Matlab/Simulink软件、丁少华等[18]采用MSC.Easy5软件、王相亭[19]采用AMESim软件对支架的立柱控制系统进行了仿真，立柱在达到设定值后出现压力下降和波动现象。随着工作面的推进，支架负载不是恒定不变的，而是实时变化的，这将频繁造成立柱压力的波动。图2(a)为采集的口孜东煤矿121302工作面ZZ13000/27/60D型支架第80号支架某一升立柱撑紧顶板过程的立柱压力值；图2(b)为采集的金鸡滩煤矿2-2上117工作面ZFY21000/35.5/70D型支架的第5号、70号、140号支架某一升立柱撑紧顶板过程的立柱压力值。由图2可知，立柱初撑力不仅达不到设定值，而且撑紧顶板后存在压力降和波动现象。

图2 立柱压力监测值Fig.2 Monitoring value of leg pressure

1.2 立柱电液力控制系统数学模型

口孜东煤矿和金鸡滩煤矿是目前很有代表性的智能化矿井，液压支架的智能化配置也非常先进，但从2个矿的液压支架升柱过程发现，采用具有补压功能的电磁换向阀，立柱仍然存在明显的初撑力压力降和波动现象。将图1中电磁换向阀5替换为三位四通电液伺服阀，立柱控制系统即成为电液力伺服控制系统。由于立柱上下腔的有效作用面积不同，属于非对称缸，假设以下条件：

(1) 乳化液的温度、黏度和体积模量为常量；

(2) 乳化液在高压胶管中的流动为紊流[20]；

(3) 忽略电液伺服阀与立柱间的胶管内乳化液的动态和压力损失；

(4) 立柱工作腔内压力处处相等。

基于以上假设条件，得到立柱电液力控制系统的电液伺服阀流量、立柱流量、立柱活塞力平衡3个方程，对方程进行拉普拉斯变换[21-22]得

(1)

式中，QL为负载流量，m3/s；Kq为流量增益，m2/s；Kc为流量-压力系数，m3/(s·Pa)；Xv为阀芯位移，m；PL为立柱控制腔压力，Pa；Ac为立柱活塞有效作用面积，m2；Xc为立柱活塞位移，m；Fc为立柱输出力，N；Ctc为立柱总泄漏系数，m3/(s·Pa)；V0为控制腔初始容积，m3；βe为乳化液体积模量(包含腔壁、管壁弹性变形的效应)，N/m2；mt为总惯性负载，kg；Bc为总黏性负载系数，N/(m·s-1)；K为弹性负载，N/m。

式(1)消去中间变量QL和Xc，可得阀芯位移Xv与立柱输出力Fc的传递函数Gp(s)为

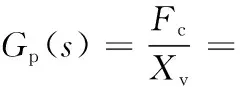
Kce=Kc+Ctc

(2)

通常情况下，总黏性负载系数Bc很小，可忽略不计。如果再满足

(3)

(4)

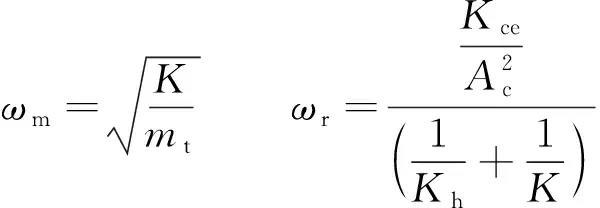
式中，ωm为负载固有频率；ωr为液压弹簧与负载弹簧串联偶合的刚度与阻尼系数之比；ω0为液压弹簧与负载弹簧串联偶合的刚度与负载形成的固有频率；ωh为液压固有频率；ζ0为阻尼比；Kq/Kce为总压力增益。

由此可得系统的开环传递函数为

(5)

式中，Ka为伺服放大器的增益；Kf为传感器的增益；Kv为电液伺服阀的流量增益；K0为系统开环增益；Gv(s)为电液伺服阀的传递函数。Gv(s)的形式取决于动力元件液压固有频率的大小，当电液伺服阀的频率与液压固有频率接近时，Gv(s)可近似为二阶振荡环节；当电液伺服阀的频率大于液压固有频率3～5倍时，Gv(s)可近似为惯性环节；当电液伺服阀的频率大于液压固有频率5～10倍时，Gv(s)可近似为比例环节。

多数电液伺服系统的伺服阀动态响应往往高于执行元件，为了简化分析和设计，伺服阀的传递函数一般采用二阶振荡环节。

2 系统性能分析

以口孜东煤矿121302工作面的ZZ13000/27/60D型支架为例对系统进行性能分析。《煤矿安全规程》规定，工作面液压支架的初撑力不应低于泵站压力的80%，考虑到乳化液泵站到液压支架的压力损失[23]，设定初撑力的下限值为22 MPa，其他参数如下：

(1) 支架立柱缸径为φ360 mm/φ270 mm，柱径为φ340 mm/φ230 mm，泵站压力为31.5 MPa，初撑力为12 825 kN，工作阻力为13 000 kN，计算得Ac=101 787.60 mm2。

(2) 升立柱100 mm，单根立柱负载质量取 223×103kg(22 MPa)，负载弹簧刚度3.2×106N/m(31.5 MPa)，乳化液体积模量βe=2 200 MPa。

(3) 压力传感器增益Kf=9.4×10-6V/N。

(4) 电液伺服阀固有频率ωv=628 Hz，阻尼比ζv=0.5，流量550 L/min，额定电流40 mA，Kq= 27 000L/(min·m)，Kce=0.06 L/(min·MPa)，伺服阀流量增益Kv=12.5，系统开环增益为

考虑误差，取K0=25。进而计算ω0=53.44 Hz，ωm=3.96 Hz，ωr=0.000 11 rad/s，ζ0=0.014，并将参数代入式(5)可得系统开环传递函数。利用MATLAB编程绘制系统的奈奎斯特图(Nyquist)、零极点图(Pole-Zero)、伯德图(Bode)，以及单位阶跃响应(Step Response)和单位脉冲响应(Impulse Response)曲线，如图3所示。

图3 系统性能曲线及阶跃响应和脉冲曲线Fig.3 System performance curve and step response and impulse response curve

由图3(a)可知，逆时针绕(-1，j0)的圈数为0，系统稳定；由图3(b)可知，右半S平面不存在开环零点和极点，系统为最小相位系统；由图3(c)可知，系统的相位裕度为94.1°，幅值裕度为 10.7 dB。通常，系统能够可靠正常运行的相位裕度和幅值裕度必须是正值，且相位裕度不小于40°，幅值裕度不小于6 dB，系统是稳定的；由图3(d)可知，系统也是稳定的，阶跃响应需要115 s趋于稳定；由图3(e)可知，系统也是稳定的，脉冲响应90 s后趋于稳定。综上可见，建立的立柱电液力伺服控制系统虽然是稳定的，但响应速度较慢，系统快速性较差，需要采用控制方法以提高响应速度。

3 基于BP神经网络PID的控制系统设计及仿真实验

3.1 自适应控制系统设计

对上述的立柱电液力伺服控制系统引入BP神经网络加经典的PID控制，实现系统的自主学习和自适应。其控制原理：额定初撑力输入信号r与立柱下腔压力PL经转换放大的反馈信号yf相比，得到的偏差信号e和r、yf、u作为神经网络的输入，经训练学习得到PID控制器的3个参数KP、KI、KD，经伺服放大器放大后控制电液伺服阀的输出流量，驱动立柱活塞产生负载压差，使输出力向减小偏差信号的方向变化，直到输出力与期望输入相等为止，控制原理如图4所示。

图4 液压支架初撑力自适应控制原理Fig.4 Schematic of adaptive control for hydraulic support’s setting load

BP神经网络是反向传播网络(Back-Propagation Network)的简称，其将W-H学习规则一般化，属于δ算法，是一种监督式学习算法。由信息的正向传播和误差的反向传播两部分组成。在神经网络的实际应用中，80%～90%的网络模型采用BP网络或其变化形式[24]。典型的神经网络包含输入层、隐含层和输出层3部分。其中，输入层和输出层的神经元数目是由所要解决的问题决定的，隐含层的层数及每层的神经元数是由设计者决定的。如果隐含层的神经元数取的足够多，能够训练出任意输入和输出之间的有理函数关系。

神经网络的误差精度可通过增加神经网络的层数或增加隐含层的神经元数目得到提高和改善。增加神经网络层数势必增加网络的复杂程度，而增加隐含层的神经元数目会使训练效果更易观察和调整。一般情形下，优选增加隐含层的神经元数目。隐含层的神经元数目不能过多，也不能过少，一般按式(6)选取：

(6)

式中，r为输入层神经元数；s为输出层神经元数；s1为隐含层神经元数。

3.2 控制器的算法

综上分析，本文采用三层BP神经网络。由图4可知，系统的输入由r、yf、e、u4个参数决定，因此神经网络的输入层神经元数为4个；希望得到PID控制器的3个参数KP、KI、KD。因此，神经网络的输出层神经元数为3个，隐含层神经元数初步确定为12个。

BP神经网络的激活函数必须是处处可微，即一阶导数存在，常采用Sigmoid型对数函数、tanh型双曲正切函数和线性函数。PID控制器的3个参数KP、KI、KD不能为负值，因此神经网络的输出层激活函数可采用Sigmoid函数，隐含层激活函数可采用双曲正切tanh函数。

图4所示的控制系统包含2个控制器，即经典PID控制器和神经网络控制器。经典PID控制器直接对被控对象进行闭环控制；神经网络控制器根据系统运行的状态，调节PID控制器的3个控制参数。通过神经网络的自学习和权值系数的调整，实现系统的最优稳定运行。具体算法如下：

(1) 经典PID控制算式[25]为

u(k)=u(k-1)+KP[e(k)-e(k-1)]+
KIe(k)+KD[e(k)-2e(k-1)+e(k-2)]

(7)

隐含层第i个神经元的输出为

(8)

输出层第k个神经元的输出为

(9)

式中，o1=KP；o2=KI；o3=KD。

误差函数(性能指标)为二次型，即

(10)

(2) 权值系数按有监督的Hebb学习规则进行，采用梯度下降法对输出层和隐含层的权值系数进行更新。

输出层第i个输入到第k个输出的权值，有

(11)

同理可得偏差增量为

(12)

隐含层第j个输入到第i个输出的权值，有

(13)

同理可得偏差增量为

Δb1i=ηδij

(14)

将上述算法进行规范化处理以保证其收敛性和鲁棒性，即

(15)

x1(k)=e(k)-e(k-1)

x2(k)=Δe(k)

x3(k)=e(k)-2e(k-1)+e(k-2)

z(k+1)=e(k+1)。

对比例器P、积分器I、微分器D采用不同的学习速率ηP、ηI、ηD。

具体的算法可归纳如下：

① 确定神经网络输入层、隐含层和输出层的神经元数，并随机初始化输入层—隐含层和隐含层—输出层的权值；

② 设置期望误差最小值、最大循环次数、学习速率；

③ 给定r(k)，采样得到yf(k)，计算误差e(k)；

④ 将r(k)、yf(k)、e(k)、u(k-1)进行归一化处理并作为神经网络的输入，由式(7)和式(8)计算各层神经元的输入和输出，得到PID控制器的3个参数KP、KI、KD；

⑤ 由式(7)计算PID控制器的输出u(k)，参与控制和计算；

⑥ 采样得到r(k+1)、yf(k+1)，计算e(k+1)；

⑦ 由式(12)至式(14)修正输出层和隐含层的权值系数，置k=k+1，返回④，直到误差函数满足要求。

3.3 仿真实验

图5 初撑力响应曲线Fig.5 Response curve of setting load

采用本文的BP神经网络PID控制方法，比例权值初始值KP=0.44，积分权值初始值KI=0.22，微分权值初始值KD=0.53。当液压支架初撑力的期望输入为阶跃信号时，初撑力响应曲线如图5所示，比例、积分、微分权值变化曲线如图6所示。由图5可以看出，系统达到稳定状态需要约8.85 s，没有超调量，与没有采用BP神经网络PID控制相比，响应时间提高约13倍。由图6可以看出，比例权值和微分权值先变小再变大，最后稳定；积分权值单调减小，最后稳定。KP和KD对控制效果的影响较大，KI对控制效果的影响较小。比例权值最终稳定在KP=0.402 6，积分权值最终稳定在KI=0.215 3，微分权值最终稳定在KD=0.485 6。

图6 比例、积分、微分权值变化曲线Fig.6 Change curve of proportional，integral and differential weight

工作面向前推进过程中，支架是按“降—移—升”循环动作的，立柱压力也随之变化。为了简化分析，假设支架初撑力的期望输出是方波信号。采用BP神经网络PID控制后的输出响应如图7所示。由图7可以看出，每个循环达到稳定需要9.1 s，也没有超调量。因此，采用BP神经网络PID控制能够使支架初撑力快速、稳定地达到期望值，大大提高支架初撑力的自适应控制能力。

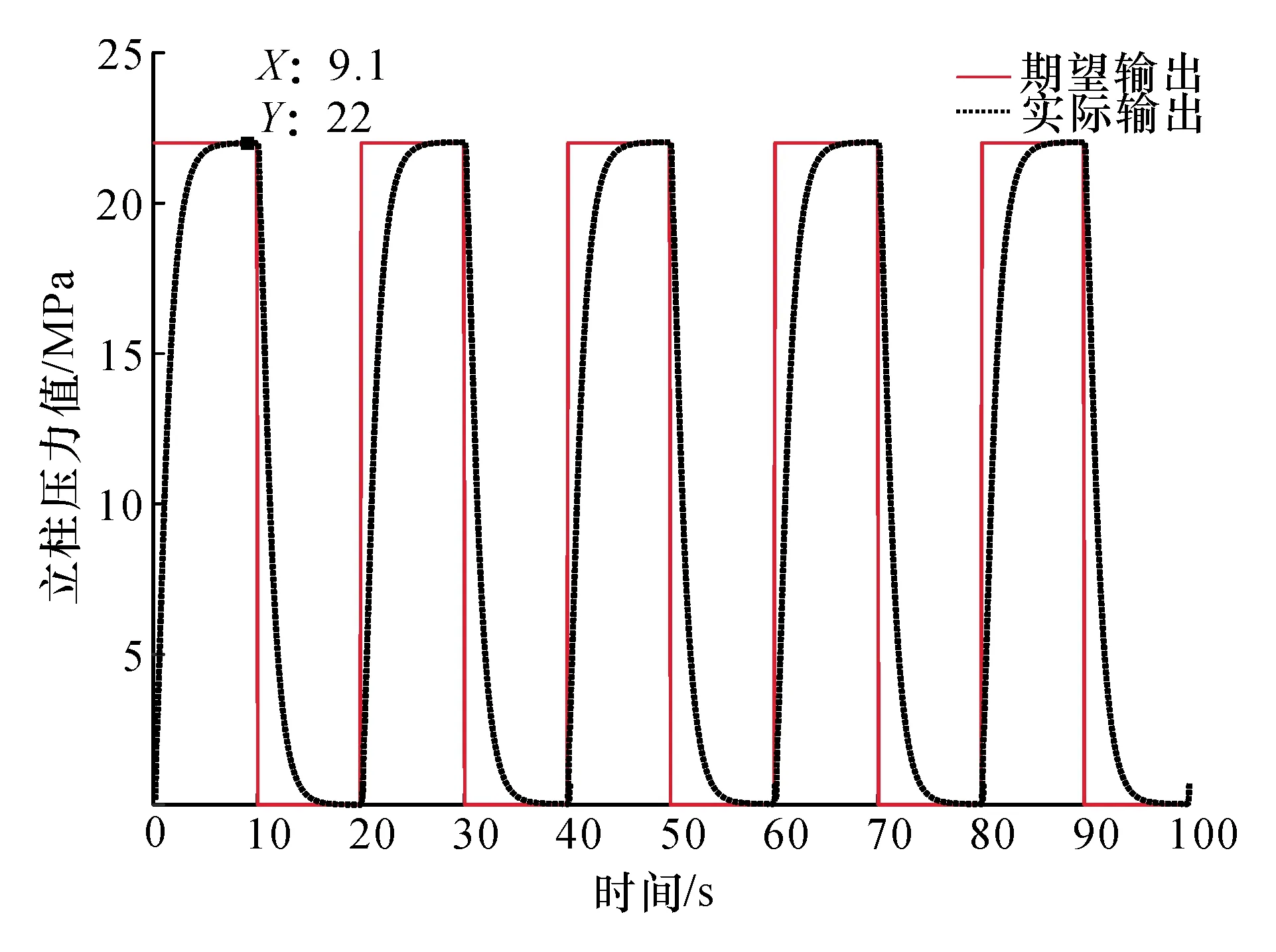
图7 期望输出为方波时的响应曲线Fig.7 Response curve with expected output of square wave

4 结 论

(1) 针对液压支架初撑力难以保证和稳定的问题，建立了立柱电液力控制系统数学模型，提出了基于BP神经网络的PID初撑力自适应控制方法，并建立了三层神经网络控制模型，采用有监督的Hebb学习规则和梯度下降法对输出层和隐含层的权值系数进行更新，经训练得到PID控制器的3个控制参数，比例权值和微分权值先变小再变大，最后稳定；积分权值单调减小，最后稳定。KP和KD对控制效果的影响较大，KI对控制效果的影响较小。BP神经网络PID控制器的3个参数最终分别稳定在KP=0.402 6、KI=0.215 3、KD=0.485 6。

(2) 分析了立柱电液力伺服控制系统的稳定性，系统的Pole-Zero图右半S平面不存在开环零点和极点，系统为最小相位系统；Nyquist图逆时针绕(-1，j0)的圈数为0，系统相位裕度为94.1°，幅值裕度为10.7 dB，该系统稳定；阶跃响应115 s趋于稳定，脉冲响应90 s趋于稳定，响应速度较慢。

(3) 立柱电液力伺服控制系统采用BP神经网络PID控制，期望输出为阶跃信号时，立柱达到初撑力设定值需要约8.85 s，并能保持稳定；期望输出为方波信号时，立柱达到初撑力设定值需要约9.1 s，并能保持稳定。与没有采用BP神经网络PID控制相比，响应时间提高约13倍。