多站超视距定位虚假定位点剔除方法研究

徐海洋 王玉梅

（1.中国船舶重工集团第七二三研究所 扬州 225101）（2.江苏科技大学 镇江 212003）

1 引言

对超视距目标定位，各侦察站往往基于对流层散射原理实现对目标的超视距侦察，再利用测向交叉定位方法［1］对目标进行定位。由于对流层的散射特性以及环境影响，各侦察站得到的目标方位值并不唯一，直接测向定位将产生虚假定位点，随着侦察站和目标数量的增多，虚假定位点数量将急剧增多［2］。

目前已有大量针对测向定位中剔除虚假定位点问题的论文［3～7］，但是由于超视距散射信号具有随机性，需要较多侦察站协同工作才能实现超视距定位，在侦察站和辐射源数量都很多的情况下，一般测向算法使用的虚假点剔除方法不再适用。对此，本文考虑采用两个步骤对超视距定位的虚假定位点进行剔除。首先利用灰色数据关联算法［9］先对同一时刻接收到的信号进行数据关联处理，将来自同一辐射源的信号进行匹配，再利用匹配后的结果进行定位计算，这一步将大大减少虚假定位点数量。然后剔除数据关联错误遗留下来的虚假定位点，由于超视距定位作用目标距离较远，且利用对流层散射信号实现超视距电子侦察的测向误差一般在0.8°～5°，若关联错误的方位角与正确方位角相差角度大于测向误差，那么使用含有关联错误的方位角得到的定位点之间的距离往往较大，根据这一几何特点，对虚假定位点进行剔除。

2 灰色关联

经验表明，不同侦察站在同一时间接收到的同一辐射源信号的特征参数具有一定的相似性，已经有许多研究人员对雷达辐射源信号的数据关联进行了研究［8～10］，灰色关联算法是一种计算复杂度低且关联正确率高的数据关联算法，也有研究人员对灰色数据关联算法进行了改进［12］，本文利用灰色关联算法对两个侦察站的超视距雷达信号进行关联匹配。下面就采用两个侦察站的超视距定位进行讨论。

设t时刻副站测得的信号的特征向量为Y(y1,y2,…,ym)，其中 yk为信号特征值，每个特征向量有m个特征值。在同一时刻（由于超视距传输时延以及信号处理时延等，这里的同一时刻指包含了时间偏差的一段时间(t -Δτ～t+Δτ)，一般到达时间差Δτ可以取到秒级）主站共测得n个信号，它们的特征向量分别为Xi(k)=(xi(k),xi(k),…,xi(k))，（i=1,2,…,n，k=1,2,…m）。将副站测得的信号传到主站进行数据关联处理。

2.1 灰关联系数

为了使不同类型的特征参数具有可比性，首先采用区间值化法对特征参数进行处理。

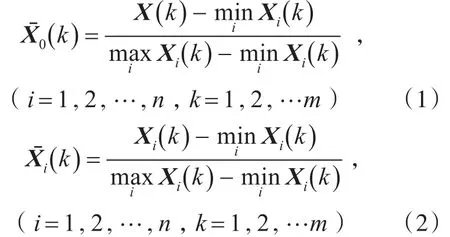
参考序列与比较序列的灰关联系数为

其中 ρ为分辨系数，ρ越大，分辨力越大，ρ的具体取值可以视情况而定，一般取 ρ=0.5。为 两 级 最 小 差 ，|为两级最大差。于是Y与Xi的关联系数为

2.2 加权灰关联度

将每一个比较数列各个指标的关联系数集中体现在一个值上以便比较，这个值就是灰关联度［10］。若认为比较数列的各个指标对于关联分析是同等重要的，即作平权处理，则用平均值法计算灰关联度，但事实上观测矢量的各个特征参数的重要性在多数情况下是不同的，因而必须进行加权处理。令a(k)，k=1,2,…n表示相应指标的权系数，且则定义加权灰关联度为

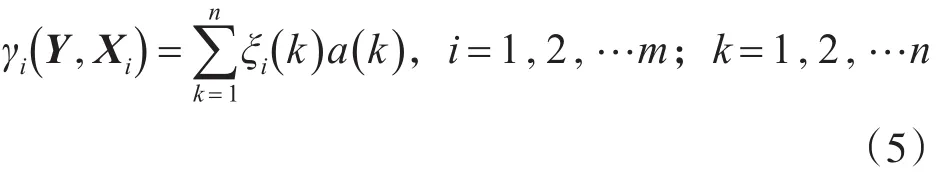
将灰关联度按从大到小排序得到灰关联序列。这里采用最大关联度识别原则，即选择满足的对象，使之最关联于Y。

在加权灰关联算法中，权重表明了不同特征在决策中的重要性，也反应了不同特征在决策中的可靠性，一般情况下，权重可以由专家根据经验主观赋值，也可以使用熵理论来确定权值大小［12］，前者不够灵活，在复杂的数据环境下可靠性不高，后者实时性好但计算量大。

2.3 仿真分析

雷达辐射源信号的信噪比对数据关联算法的关联正确率影响较大［9～12］，下面对灰色关联算法在不同的噪声环境下灰色数据关联算法的关联效果进行仿真。仿真使用20组辐射源信号参数，参数特征包括载频、重频、脉宽和信号幅度，仿真结果见表1。

表1 不同信噪比下灰色关联算法的正确关联概率

表1列出了5种信噪比下灰色关联算法的正确关联概率。在本次仿真中当信噪比大于20dB时，灰色关联算法的正确关联的概率能达到90%以上。基于对流层散射的超视距侦察定位系统，由于对流层的散射特性，各侦察站侦收到的目标方位存在非唯一性，但对流层散射以前向散射为主，其它方向散射信号很弱，可根据此特性，利用灰色关联算法对各侦察站目标进行数据关联，提高分选正确率。

为了解灰色关联算法在特征参数缺失情况下的关联效果，在仿真前随机选取信号的4个特征参数中的1～3个将其值置为零模拟数据缺失的情况。经过1000次蒙特卡洛仿真，结果如图1所示。

图1 特征值缺失情况下灰色关联算法的正确关联率

根据图1，存在1个特征值缺失时，灰色关联法的正确关联概率在信噪比大于26dB时依然能够达到90%以上。有2个特征值缺失时，正确关联概率下降到了60%以下。当特征值缺失数量超过2个时，正确关联概率已低于30%，无法有效地进行数据关联处理。因此，采用3个及以上的特征值就能够有效地进行数据关联。

3 剔除虚假定位点

由于对流层散射特性、水面环境影响以及仪器本身测量精度等因素的影响，数据关联正确率难以达到百分之百，需要对错误关联的方位角计算得到的虚假定位点进行二次剔除。

虚假定位点示意图如图2所示。S1、S2、S3、S4为四个侦察站，目标位于T处。

图2 虚假定位点示意图

根据图2，若数据关联没有错误，由4个侦察站两两组合得到的目标位置理论上集中于T处。而若S1测得的数据不是来自于目标T，并且其所测数据中的方位角与目标T的方位角相差较大时，含有S1测得的方位角的组合得到的目标位置则较为分散，即图3中点T1,2、T1,3和T1,4处。根据这一特点，若含有某一侦察站数据的定位点两两之间距离均大于某一门限值，则认为这些定位点均为虚假定位点。

3.1 方法描述

采用N个侦察站S1～SN进行定位，则对这N个方位角有n=C2N种组合情况，经过定位计算可得n个目标位置。假设侦察站Sm测得的数据关联错误，由于错误关联数据中的方位角可能与真实目标方位角的偏差较大，那么根据图2所示几何关系，含有Sm组合得到的（N-1）个虚假定位点间的距离将会较大。本节给出了利用每种组合得到的目标位置之间的距离的大小来剔除虚假定位点方法，具体过程如下：

步骤1：求出所有组合计算得到的目标位置（ Lti,j，Bti,j），（i=1,2,…N ，j=1,2,…N ，且j≠i），（N为侦察站数量，下标i和j表示第i和j个侦察站的组合）。

步骤2：分别计算出侦察站Si与其它各站的组合得到的目标位置两两之间的距离：

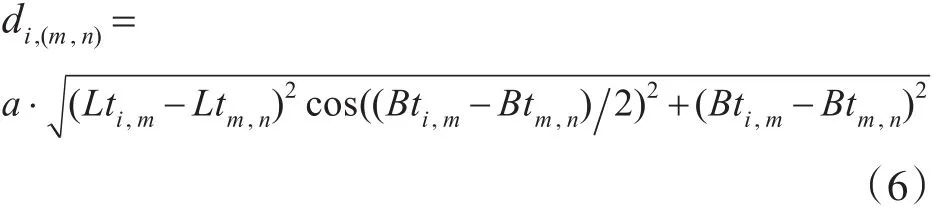
其中a为地球椭球的长半轴长，i、m、n=1,2,…N ，i≠m≠n，得到矩阵 D ：

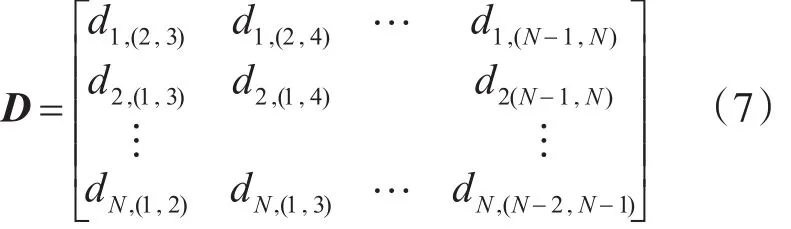
步骤3：求矩阵C：

设置门限 ηd，若 Di,j＞ηd，则 ci,j=1 ，否则ci,j=0，其中b=。门限值ηdmax的选取需根据侦察站测向精度以及经验进行选取，本文仿真时选取矩阵D中数据的平均值作为门限。

步骤4：对矩阵C每行求和，得到列向量P=[p1p2… pN]T，若 pi=N，则认使用含有第i个侦察站的组合得到的定位结果均为虚假定位点，需要将其剔除。

需要注意的是，2个侦察站只能得到一个定位点，无法使用该方法判断该点是否为虚假定位点；使用3个侦察站定位能得到3个定位结果，若其中一个侦察站的数据关联错误，那么这3个定位点间的距离将相差较远，虽然能判断出存在一个站的数据关联错误，但无法判断是哪个侦察站。因此，当用于定位的侦察站数量少于4时无法使用上述方法进行虚假定位点的剔除。

3.2 仿真分析

设置每个侦察站的测向误差为1°，站址误差20m，假设侦察站S1的数据错误，选取错误关联数据中的方位角相对实际方位角偏移了10°、90°、120°和210°这四种特殊情况，使用上述方法进行1次仿真，结果如图 3（a）～（d）所示。

图3 剔除虚假定位点示意图

根据图 3（a）～（d），每个图中用圆圈出的4个点即为采用上述方法需要剔除的定位点，发现这4个点与S1位于同一直线上，因此可以判定来自侦察站S1的数据关联错误。所以使用本文的方法能对超视距定位的虚假定位点进行有效剔除，还能判断出关联错误的数据来自于哪个侦察站。

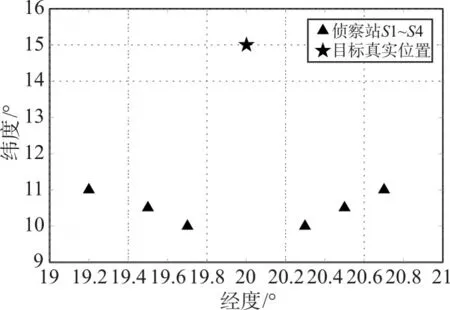
图4 侦察站布站示意图

为研究错误关联方位角与正确方位角的差值对正确剔除虚假定位点的影响，按图4布站，设置每个侦察站的测向误差均为1°，站址误差20m，依次设置侦察站S1～S6的数据关联错误，使用Matlab进行1000次蒙特卡罗仿真实验，仿真结果如图5和图6所示。根据图5和图6，角度的差值在0～180°和180°～360°的图形具有对称性，这是由于测向方位面算法中使用了反正切函数，而使得角度差为θ和360°-θ的效果相同。另外由于每个侦察站与目标的相对位置不同，使得每个侦察站数据发生错误关联时通过统计方法得到的正确剔除虚假定位点的概率不尽相同。

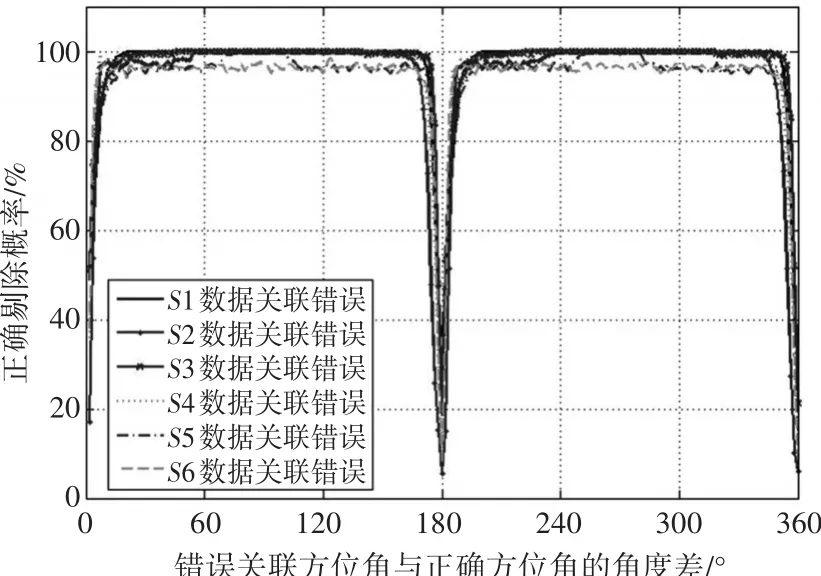
图5 虚假定位点剔除情况与方位角偏离的关系

根据图6，当错误关联数据中的方位角与正确方位角的角度差约在10°～170°以及190°～350°范围内时（若目标及舰艇编队相对位置不同，该范围可略有几度内的偏差），虚假定位点得到剔除的概率能达到95%以上。因此采用上述方法能够对超视距定位中由关联错误遗留下来的虚假定位点进行有效剔，消除虚假定位点对最终定位结果的影响，从而达到减小定位误差的效果。

图6 虚假定位点剔除情况与方位角偏离的关系（局部放大图）

4 结语

本文对多站超视距无源定位的虚假定位点剔除方法进行了研究，提出先对测量参数进行数据关联，然后针对数据关联遗留的虚假定位点进行二次剔除的假点剔除方法，并进行了仿真分析，结果表明该剔除虚假定位点的算法能够较为准确地实现多站协同超视距测向定位中虚假点的剔除，具有一定的理论指导意义，在实际利用时可根据实际情况，合理选择信号参数的权系数，提高定位精度。