基于NSGA-Ⅱ及BP神经网络的引擎盖外板定位点优化

李沛，邢彦锋，杨夫勇

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

在汽车车身中，引擎盖是必不可少的关键部件，引擎盖板不仅要与汽车的前保险杠、前大灯等配合良好，还要求在包边后有非常好的密封性。无论是压合模包边还是包边专用机包边，亦或使用机器人滚边等工艺对引擎盖内外板进行包边，都需要对内板和外板进行装夹定位，所以定位点及夹具的布置至关重要。在汽车和航天制造中会采用大量的钣金件，以此减少自身的质量，目前在汽车制造中使用的钣金件因尺寸较大、刚度较低等原因，钣金件在装夹过程中难免发生变形，因此合理的夹具定位方案限制钣金件的过度变形尤为重要。过去几十年间国内外众多学者对夹具进行了大量研究，其中螺旋理论自由度分析原理、数值分析方法、非线性规划方法、有限元分析等方法的运用使夹具研究工作越来越完善。

Chou[1]等利用螺旋理论和工程力学理论，建立了棱柱形零件加工夹具自动配置的数学理论；Cai[2]等提出了一种稳健夹具设计的微分方法，使得零件误差引起的结果误差最小化；Xiong[3]等提出了抓取稳定性评价指标以保证稳定地抓取，并且给出了一种求解最优接触形态的非线性规划方法；Wang[4]等为了分析钣金夹具定位布局的响应变形，提出了一种RBF 神经网络预测模型，以此优化钣金夹具的定位布局；Huang[5]等采用一种新的可变顺序空间填充算法搜索最优设计，并利用提出的方法进行夹具稳健设计；邢彦锋[6]等应用目标检测算法two-stage 方法优化钣金零件的定位布局，减少了钣金件有限元分析的次数；秦国华[7]等针对夹具布局，以夹具稳定性为核心，提出了逐点设计算法，该方法适用于各类具有复杂曲面的工件，同时还可以拓展计算机辅助夹具设计的理论和技术；姜昂等[8]采用定位点搜索算法寻找最佳的定位点位置，但是该方法需要在所有定位点中逐个筛选，搜索效率低。上述方法多采用数值分析方式寻求稳健的定位方案，在揭示其各参数的共性规律时略显不足，因而Wan[9]等采用奇异值分解方法求解六自由度工件的误差放大因子，从误差放大系数、误差性能指标、位置稳定性3 个方面表征定位器布局特征、提高工件定位精度和夹具布局稳定性，从而揭示夹具配置的一般规律；林嘉[10]等通过确定性定位误差分析模型，在引入两个假设的基础上得到了三维工件空间三维定位方案稳健设计的一般解，但是该方法只获得了稳健定位的解析式，未能详细说明夹具的布置措施。

在目前的钣金件定位布局研究中多采用数值的方法寻找稳健的定位方案，优化定位点时，使用定位点搜索的算法使得计算的效率不高，优化目标往往只有一个。本文通过使用遗传算法优化制造误差方差及位置稳定性参数，先对主定位基准面上前3 个定位点进行优化，再利用BP 神经网络对第四个定位点进行预测，最后分析UG 位移结果图确定第4 个定位点的具体位置。

1 定位点布局的稳定性

稳健的夹具定位设计的目的是寻找主定位基准面上定位点位置和第2 定位基准面上2 个定位点位置，以及第3 定位基准面上最后一个定位点位置。

1.1 “N-2-1”定位

对于不用考虑变形的刚性工件可以采用“3-2-1”定位原理来进行确定性定位，而对于薄壁柔性工件来说其本身刚性小且易变性，甚至在自身重力作用下也会发生形变，因而传统的“3-2-1”定位原理就很难满足柔性工件的加工需求。由于考虑到柔性工件自身的特点，并且柔性工件会因重力原因在法向方向上会产生变形，因此在第1 定位基准面上的定位点数为N（N＞3），在第2 定位基准面上的定位点数为2，在第3 定位基准面上的定位点数为1，以此来完成对柔性工件的过度约束。

1.2 雅克比矩阵

针对三维工件的6 个确定性定位，在引入2 个假设条件的基础上推导了雅克比矩阵。

在三维空间坐标中根据定位点的位置、方向确定一个包含各定位点位置坐标、控制方向的矩阵称为雅克比矩阵。在三维空间中，雅克比矩阵如下：

6 个定位点的控制方向为

加工过程中，工件会受到各种力的作用，如重力、切削力和力矩等，定位点的布局决定了工件的自由度。在工件夹具系统中,定位点的个数为n，第i 个定位点的位置为Ii=[xi，yi，zi]T（i=1，2，…，n），ni=[nix，niy，niz]T是工件与定位点在ri接触点处的单位法向量，则定位矩阵为H=[H1，H2，…，Hn]，其中Hi=[niT，（Ii×ni）T]T，将6 个定位点的控制方向代入定位矩阵中有

1.3 位置稳定性参数及制造误差方差

根据“3-2-1”定位原理，要限制一个物体的平动和转动，需要限制它的6 个自由度，只有当它的6 个自由度都被限制，物体才能保持平衡，即当工件被确定性定位时，雅克比矩阵J 是非奇异的。Xiong[11]给出了在当前布局中衡量定位器稳定性的计算方法：

因为H 是满秩的，所以稳定性参数为W=‖H‖，对于薄板工件，稳定性参数[12]为

对式（1）中的雅克比矩阵求逆可得式（6）：

式中：P1=x1y2-x2y1+x2y3-x3y2+x3y1-x1y3；P2=（x4-x5）（y2-y3）z6-（x2-x3）y6（z4-z5）；P3=（x4-x5）（y3-y1）z6-（x3-x1）y6（z4-z5）；P4=（x4-x5）（y1-y2）z6-（x1-x2）y6（z4-z5）；P5=x4-x2，P6=z4-z5，ς1=x5z4-x4z5。

控制z 方向的定位点1、2、3 沿其z 方向的制造误差的方差为D（z），定位点1、2、3 的坐标x1、y1、x2、y2、x3、y3对D（z）有影响，则

式中：ς2=x2y3-x3y2；ς3=x3y1-x1y3；ς4=x1y2-x2y1。

1.4 薄板定位布局的评价函数

钣金零件在加工过程中面临着各种尺寸问题，其中主要的尺寸问题来自自身法向方向的变形，对于一些尺寸较大的钣金零件因受自身重力影响产生的变形也不可忽略；因此对于钣金零件的加工定位方式通常采用“N-2-1”定位原理，为防止在装夹过程中工件过度变形，钣金零件的主定位基准面上的定位点数应为N（N＞3），所以被加工的钣金零件会始终处于一个过度约束的状态。参见图1。

为评价不同薄板件定位布局方案的优劣，将零件所有的有限元节点在法向方向的变形作为一个评估函数

式中：F（X）——薄板零件变形的评估函数；X——第N 个定位点的位置向量，X=[X1，X2，…，Xn]；M——薄板零件中划分的网格节点数目；ωi——第i 个节点处的法向方向的变形。

2 NSGA-Ⅱ算法及BP 神经网络在引擎盖外板定位中的应用

薄板件因自身特点，即使只受重力的情况下也会发生形变，为了评价薄板件定位布局的优劣，引入一个评估函数对薄板定位布局进行评价，通过NSGA-Ⅱ遗传算法和BP 神经网络预测定位点位置。

2.1 NSGA-Ⅱ算法及BP 神经网络介绍

NSGA-Ⅱ算法是多目标遗传算法中使用最多应用最广的一种多目标优化遗传算法，在对多个目标进行优化的问题中，由于各目标之间会存在相互制约等问题，往往会让其中一个目标得到改善，而另一个目标就会损失掉目标性能，因此多目标遗传算法的核心就是要协调好多个目标之间的关系，使得它们能找出尽可能小或者尽可能大的函数解集。

BP 神经网络是按照误差逆向传播算法训练的多层前馈神经网络[13]，它包含输入层、隐藏层和输出层3 层结构，是目前应用最广泛的神经网络。

2.2 NSGA-Ⅱ算法对主定位基准面上定位点的优化

在MATLAB 中，通过NSGA-Ⅱ算法对Fi求最小值，详细参数设置为：设置一个种群大小为100的种群，最大迭代次数为300，停止迭代为300，适应度函数偏差 TolFun 设为1×e-100，最优个体系数设置为0.5，交叉和遗传的概率分别是0.8 和0.1，优化的函数目标式是1/｜H｜、D（Z），函数的约束条件为x1，x2，x3∈（0，150），y1，y2，y3∈（0，150）。运行程序得到Pareto 前沿图，如图3 所示。

表1 部分帕累托解Tab.1 Pareto solution set

2.3 BP 神经网络构成

BP 神经网络可以根据每次训练得到的结果同设定的预测值进行比较，通过误差分析再对权值和阈值进行修改，因而可以逐渐获得输出值和预测值一致的模型。参见图4、图5。本文先对汽车引擎盖外板进行定位约束，在UG12.0 中得到仿真分析模型，通过求解各测点的坐标位置计算测点的法向位移，进而获得各测点在特定边界条件下的变形量，然后将引擎盖外板的主定位基准面上的第4 个定位点的坐标值作为BP 神经网络的输入，引擎盖外板各测点的变形量作为BP 神经网络的输出。

2.4 第4 个定位点的优化

由于外板是冲压形成的一块整体，厚度较小，故采用“4-2-1”定位布局，根据NSGA Ⅱ算法得到前3 个定位点的位置，分别是（134.689，10.577，7.965）、（125.273，139.677，6.832）、（16.834，23.781，7.091）。优化第4 个定位点时，先在外板的主定位面上确定一个近似的最优区域，以此大致确认第4 个定位点所在的区域，再BP 神经网络确认第4 个定位点的分布位置。

首先在引擎盖外板上的最优区域中选取40 个候选节点作为样本数据，由于引擎盖板在自身重力变形下也会产生变形，且在装配过程中会受到若干力的影响，因此在引擎盖的中心位置垂直于法向方向处施加一个50 N 的力，以第4 个定位点的坐标作为神经网络的输入，以各测点的法向变形量为BP 神经网络的输出，在此选取30 组数据作为神经网络的训练样本，其余的10 组数据则构成测试样本，最后借助MATLAB 神经网络工具箱得到薄板定位布局的预测模型，输出曲线和相应的相对误差如图6 所示。

为具体确定第4 个定位点的位置，本文通过遗传算法预测第4 个定位点的坐标，将BP 神经网络训练的结果同遗传算法获得的预测值进行误差分析，经过UG12.0 代入4 个定位点的坐标位置，设置约束载荷，最后求解出第4 个定位点的位置为（143.126，8.672，7.243）。神经网络的训练数集和测试数集如表2、表3 所示。

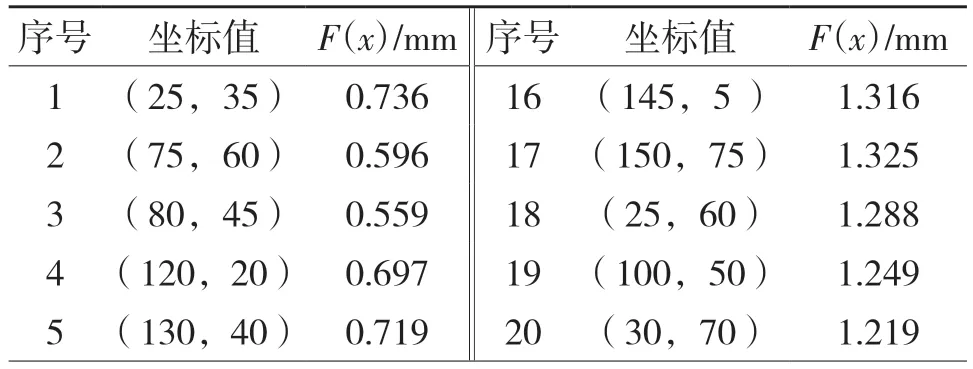
表2 训练数集Tab.2 Training sample

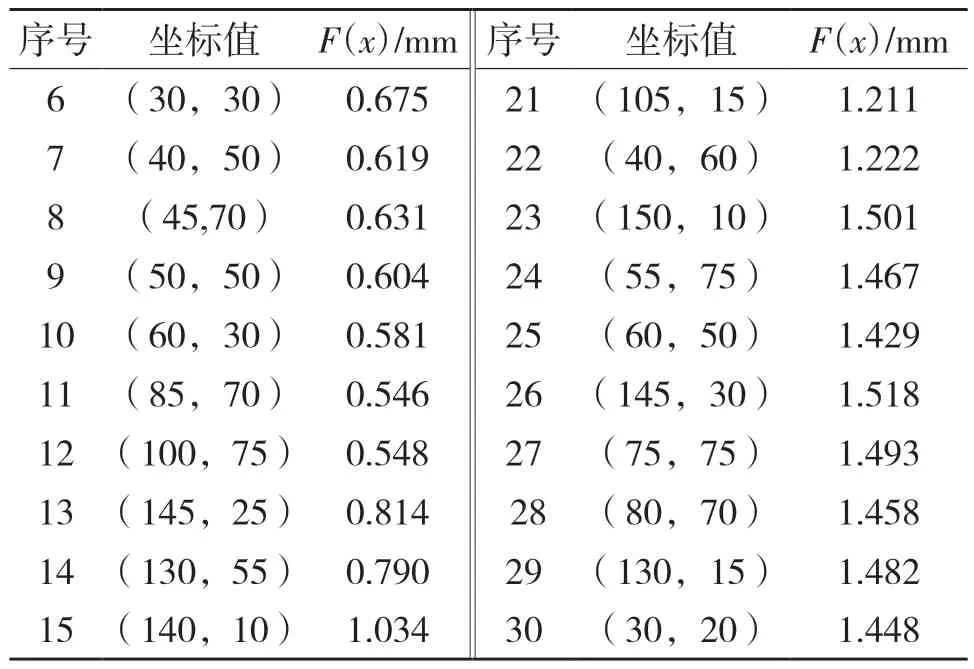
（续表）

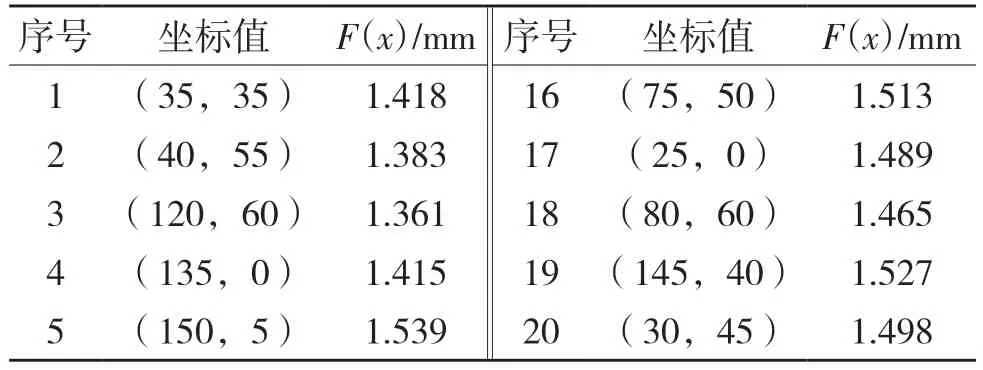
表3 测试数集Tab.3 Testing sample

3 引擎盖内板定位仿真与实验验证

汽车引擎盖板的定位布局直接影响引擎盖板与汽车翼子板、汽车前大灯及前格栅等的尺寸匹配，以某汽车引擎盖外板为例，材料为45 号钢，厚度为0.7 mm，质量密度（RHO）为7.829×10-6kg/mm3，杨氏模量为2.069 4×10-8，泊松比为0.288。为分析不同定位方案下钣金件的变形情况，利用UG12.0对引擎盖进行仿真分析，创建CAE 体4 072 个，网格单元数为85 231，在NX nastran 的求解方案下获得了不同定位布局下引擎盖板的变形情况。由图7 可见优化前引擎盖外板定位方案变形的情况与优化定位方案之后的变形情况，经优化定位布局的引擎盖外板的最大形变比优化前减少了30.89%。

4 结论

本文基于制造误差方差构建了稳健的夹具定位方案，运用NSGA-Ⅱ算法优化夹具前3 个定位点，通过BP 神经网络预测第4 个定位点，结合引擎盖外板的法向变形情况验证其合理性。最终得到如下结论：

（1）基于主定位基准面上的制造误差的方差最小化及位置稳定性参数的倒数最小化，通过多目标优化遗传算法确定了主定位基准面上前3 个定位点的布置。

（2）因为NSGA-Ⅱ算法中获得的帕累托前沿受初始种群的影响，且初始种群会有随机性，所以该方法可以得到不同的定位方案，这有利于实际生产运用。

（3）仿真模型与实际零件的对比可以更加直观地说明该方案的可行性。

本文提出的一种基于制造误差方差的薄板定位布局方案仍有不足之处，尚未涉及夹紧力且未考虑偏差补偿问题，实际结果与仿真分析结果存在些许误差，未来如何在顾及夹紧力与偏差补偿的情况下对前定位点进行优化是需要进一步研究的问题。