基于分数傅立叶变换的通信抗干扰性能研究
2020-11-09孙永林李大成
孙永林,李大成,刘 飞
(1.海装重大专项装备项目管理中心,北京 100089;2.海装装备项目管理中心,北京 100089;3.中国人民解放军32380部队,北京 100072)
0 引言
由于电磁波具有开放性,在传输过程中存在极易被干扰的现象,而良好的抗干扰性能是安全稳定通信的重要保证。随着通信种类的不断增多和通信设备的不断增加,通信易被干扰的问题已经成为制约通信发展的重要因素,而一味用提高算法的复杂度等方式来实现抗干扰的做法也越来越具有局限性。因此,找到一种简单、有效抗干扰的调制解调方法显得尤为重要。基于新的时频分析工具-分数傅里叶变换(FRFT),Tao Ran等[1]中提出了线性调频(LFM)信号的方向估计算法。LFM信号是其初始频率随时间变化的非平稳信号。分数傅立叶变换(FRFT)是普通傅立叶变换的推广,是一个能够实现非平稳信号的能量聚焦特性的强大工具,并已用于估计LFM信号的参数[2-3]。类似于余弦信号是傅立叶变换的基本信号,LFM信号也是FRFT的基本信号, LFM信号在合适的分数傅里叶变换域中呈现脉冲状态。基于此特性,Qi Shuai等[4]提出了一种以LFM信号为载波和分数阶傅里叶变换理论相结合的实现类似于FSK调制解调的新方法。在前人的理论基础上,本文同样以LFM信号为载波,利用分数阶傅里叶变换实现类似于PSK调制解调的新方法,并分析其抗干扰性能。
1 系统模型
系统模型主要由3个部分组成:信号发送端Alice、信号接收端Bob和信号干扰端Eve。假设在相同干扰信号的情况下,信号发送端和接收端分别以余弦信号作为载波利用傅立叶变换实现调制解调,和以LFM信号为载波利用分数傅里叶变换实现调制解调, 在两种不同的情况下仿真计算信号接收端Bob的误码率大小,分析其抗干扰能力。系统模型如图1所示。
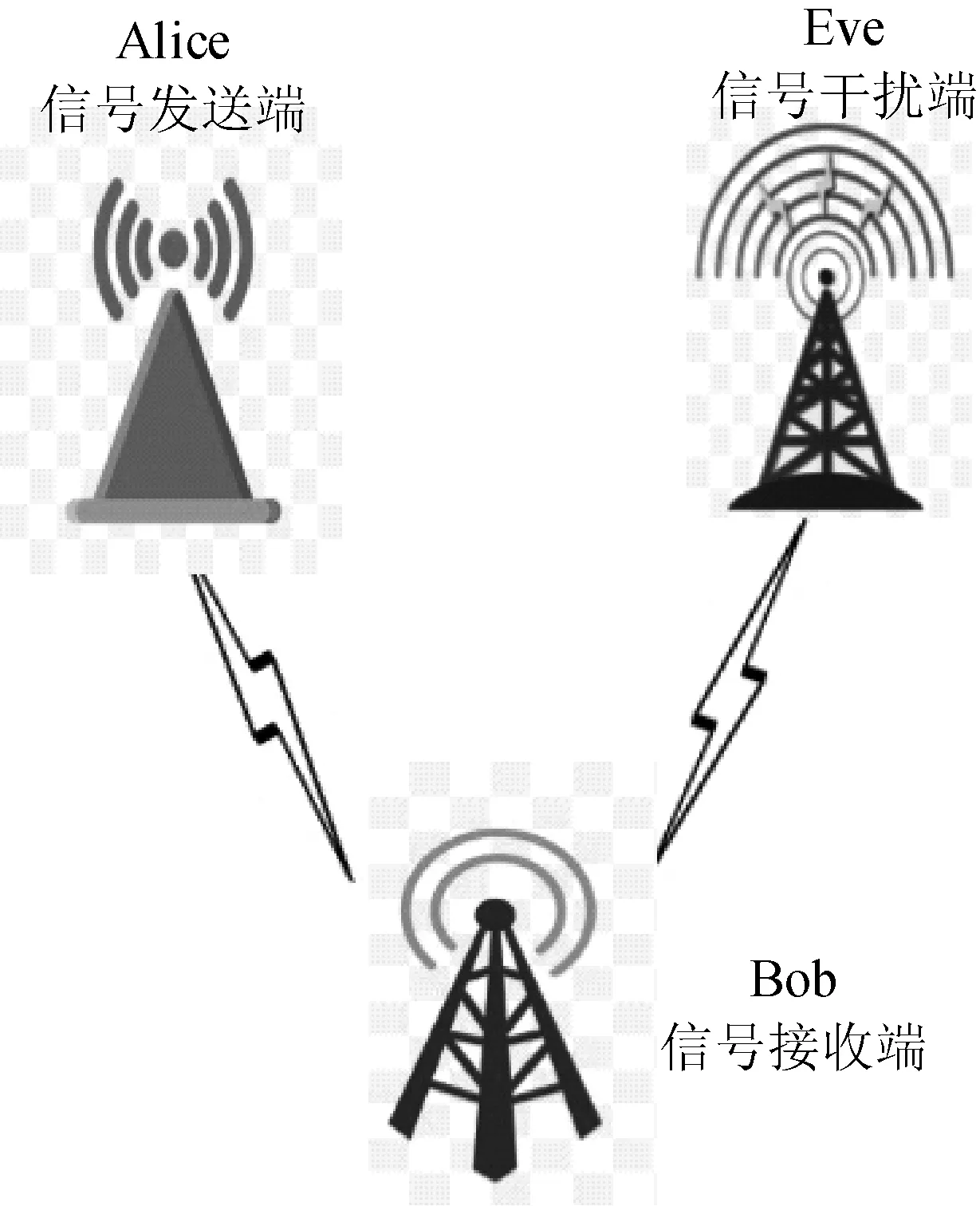
图1 系统模型
2 基本原理
2.1 LFM信号的表示
线性调频信号可以表示为:
f(t)=Aexp[j(φ+2πf0+mπt2)]
(1)
式中A是信号幅度;φ为初始相位;f0为初始频率;t是时间;m为调频率,是对应于频率的常数。 信号的瞬时频率为:
f=f0+mt2/2
(2)
2.2 FRFT算法
近年来,FRFT在信号处理领域引起了越来越多的关注,Namias介绍了FRFT的数学定义[5]。分数阶傅里叶变换的定义可以写为:
(3)
式(3)中,α为分数傅里叶变换的旋转角度。
为了便于理解,分数傅里叶变换可以分解为以下三步:
第一步:用Chirp信号对f(t)信号进行调制:
g(t)=f(t)exp[-jπt2tan(α/2)]
(4)
第二步:将调制信号与另一个Chirp信号进行卷积:
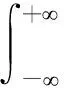
(5)
第三步:通过LFM信号和信号的卷积实现调制:
Fp(u)=g′α(u)exp[-jπu2tan(α/2)]
(6)
为了实现分数傅里叶变换的数值计算,可以将整个过程进行如下处理。
步骤一:对f(t)信号进行采样。分数阶数p的取值范围为p∈[-1,1],分数阶傅里叶变换的旋转角度与阶数的关系为:
α=pπ/2
(7)
F4[f(t)]=F0[f(t)]=f(t)
(8)
F2[f(t)]=f(-t).
(9)
也即分数傅立叶变换具有旋转特性,所以当分数阶数p取其他值时,可以先利用此特性变到[-1,1]的范围内再进行计算。
步骤二:利用FFT来实现式中的卷积运算,由此来保证通信的实时性。
步骤三:将卷积后的信号进行调制,再利用前后的抽取和内插便可得到最终的离散的分数傅立叶变换的结果。
2.3 LFM信号经过FRFT的推导运算
已知LFM信号一般形式为:
f(t)=Aexp[j(φ+2πf0+mπt2)]
(10)
为了推导方便,使φ=f0=0,A=1。因此,LFM信号经过FRFT后可以得到:
(11)

(12)
可以分段表示为:
(13)
从上述推导结果可以看出,在变换阶数满足一定的关系时,LFM信号在其相应的分数傅里叶变换域表现出冲击函数的特性。
3 仿真结果及分析
3.1 LFM信号经过FRFT的结果
在仿真实验中,为了便于计算,LFM的信号参数取φ=f0=0、m=5、t∈[0,4],则LFM信号可以表示为:
f(t)=exp(j5πt2)
(14)
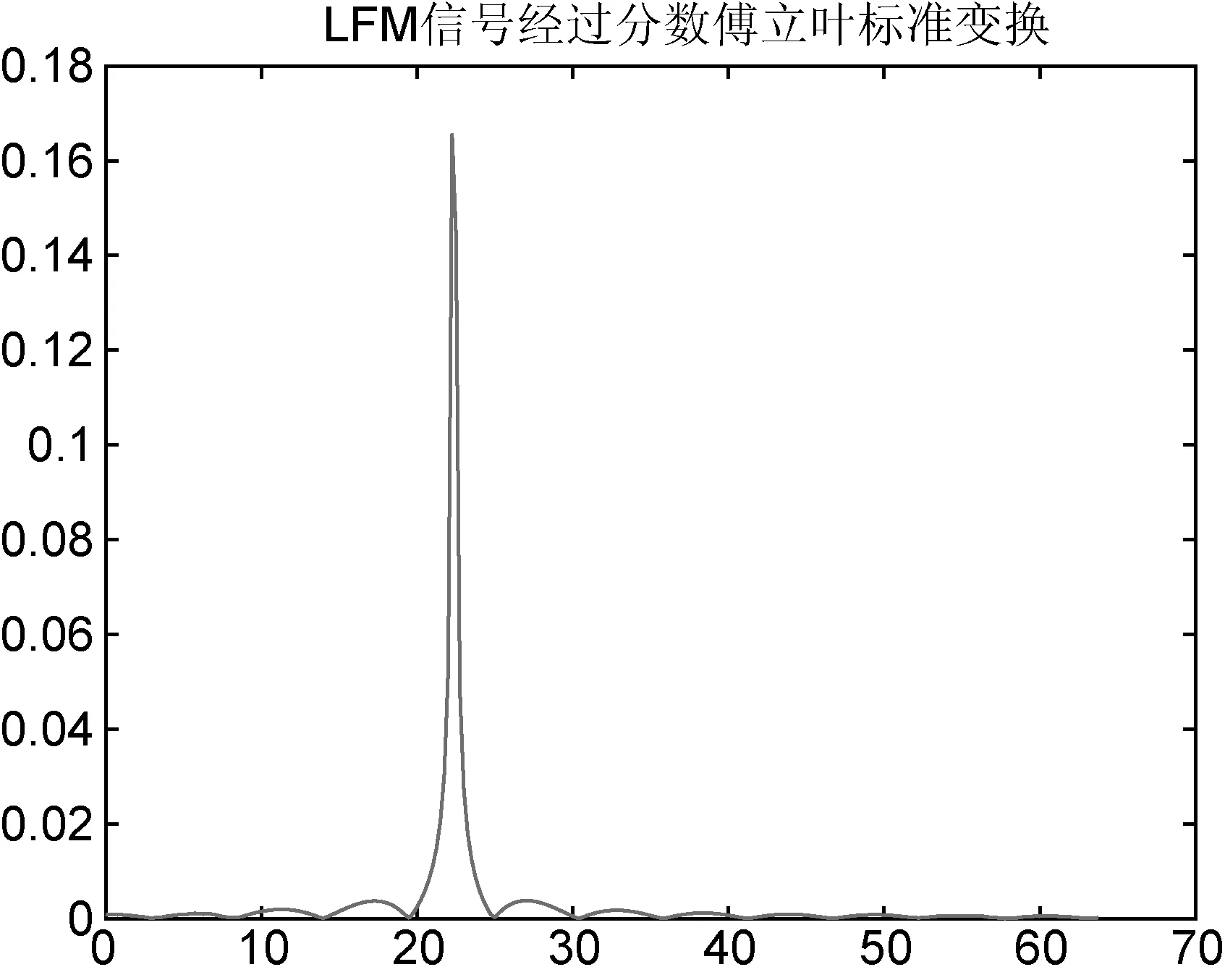
图2 LFM信号经过分数傅立叶变换
3.2 LFM信号的抗干扰性能
假设干扰信号在中心频率上,表达形式为:
g(t=Aexp(j40πt)
(15)
式中A为干扰信号的振幅。当A=1时,LFM信号与干扰信号的总信号为:
(16)
信号s(t)经过与f(t)相同的分数阶傅里叶变换后,干扰信号对LFM信号有一定的影响,但是不影响其冲击波形。总信号经过分数傅立叶变换如图3所示。
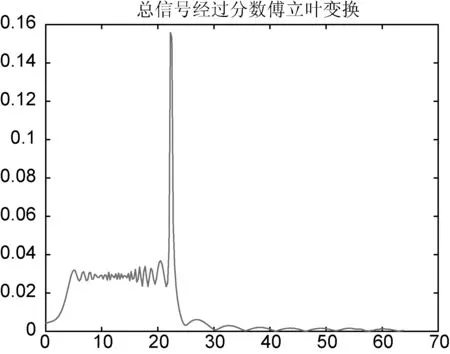
图3 总信号经过分数傅立叶变换
信号s(t)经过旋转角度为α的分数傅里叶变换后,在分数傅立叶变换域进行带通滤波,此时保留冲击信号,然后再进行旋转角度为-α的分数傅里叶变换,变换后信号恢复时域形式,在时域进行解调并判决后便得到了原信号f′(t)。LFM信号的解调原理如图4所示。
利用上述原理,对干扰信号进行仿真可以得到相应的误码率。同时,假设与LFM信号具有相同振幅的作为对比实验的表达式为:
e(t)=exp(j40πt)
(17)
在不存在噪声干扰时,e(t)信号仿真实验结果显示其误码率约0.5,即完全被干扰;而由于LFM信号只被影响了单一频点,其误码率几乎与原来没有差别,LFM信号对于单一频点的干扰具有强大的抗干扰能力。

图4 LFM信号的解调原理
4 结语
经过几十年的发展,从图像加密到频率复用再到调制解调领域,分数傅里叶变换理论已经取得了众多值得称赞的成果,本文从抗干扰的角度出发探索分数傅里叶变换理论更广泛应用的可能。首先介绍了分数傅里叶变换理论的研究现状,其次建立了现实中可能存在的恶意干扰模型,对LFM信号和分数傅里叶变换理论进行了公式推导,揭示了LFM信号经过分数阶傅里叶变换后会存在冲击函数形式这一理论基础,利用仿真结果直观展示了LFM信号在分数傅里叶变换域的冲击形式,仿真结果与理论相对应,最后,通过误码率的变化说明了干扰信号对LFM信号和余弦信号的影响大小。
虽然对分数傅立叶变换的研究已经出现了众多可喜的成果,但是其应用和影响还远不如傅里叶变换。随着人们对分数傅里叶变换研究的不断深入,更多优秀的理论成果一定会呈现在人们面前,那时,一定会带来更多的技术惊喜。
