汽车液压主动稳定杆系统的执行机构性能参数影响仿真研究
2020-11-06蔚亚,康帆
蔚 亚,康 帆
(西安航空职业技术学院,陕西 西安 710089)
汽车转弯行驶过程中,极易出现侧倾问题,从而威胁车辆与人身安全。而汽车液压式主动稳定杆系统基于传统被动稳定杆得以衍生,作为新型稳定杆系统,其可显著降低转弯时车辆侧倾的倾斜度,保障汽车行驶稳定性与安全性。目前,陈志韬等人对主动横向稳定杆试样进行了设计制造,并通过仿真提出了有效控制策略;龚建石等人通过研究构建主动横向稳定杆系统实验平台,同时根据实际情况开发了液压系统[1]。现阶段我国在主动横向稳定杆系统方面的研究依旧在不断深化,据此,本文面向汽车液压主动稳定杆系统进行了执行机构性能参数影响仿真分析。
1 主动稳定杆系统原理
1.1 系统原理
既有被动稳定杆主要是以衬套作为辅助,与车身实现有效对接,其端部则通过连杆与悬架下摆臂相连接。而主动稳定杆则基于引进液压系统,以液压缸代替了被动稳定杆的连杆。液压系统主要是由液压缸、开关阀、溢流阀、蓄能器、液压泵、油箱等所构成。
液压主动稳定杆系统原理[2]具体如图1所示。

图1 系统原理
在四个开关阀都处于关闭状态时,液压缸锁止,这时系统与被动稳定杆等效。开关阀2与3开启,开关阀1与4关闭,此时液压缸伸出,相反则缩进。液压缸伸缩极易造成稳定杆两端实现对向转动,以生成反侧倾力矩,以此与车身侧倾力度相阻抗。
1.2 控制原理
液压主动稳定杆系统控制原理即,受路面激励(q)与转向输入(γf)双重作用力,整车模型生成状态信息(车速vx、前轮转角、侧向加速度zy、车身侧倾角),基于滑模控制器计算总反侧倾力矩(Warc),动态配置于前后轴稳定杆,以Bang-Bang算法为载体有效控制推杆位移,实现反侧倾力矩的精确输出[3]。控制原理具体如图2所示。
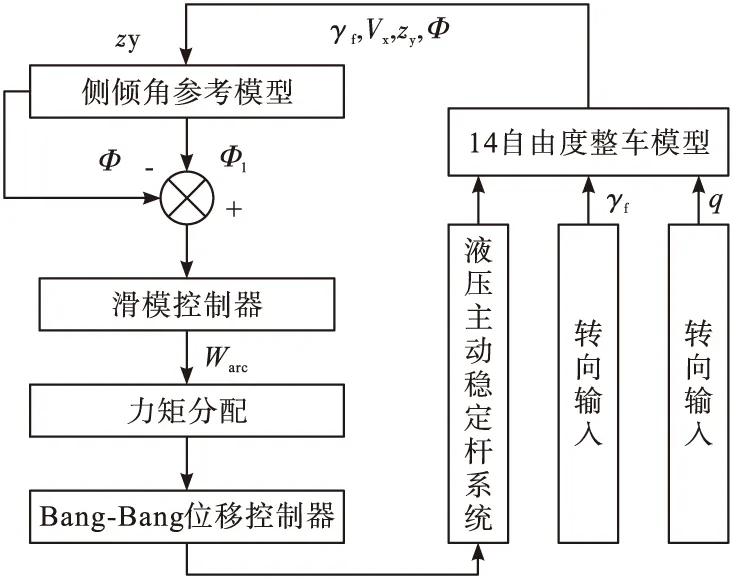
图2 控制原理
2 液压主动稳定杆系统力学性能
2.1 侧倾载荷转移量
车辆在转向时,车身的侧向加速保持在恒定状态,离心力作用在质心上。受簧下质量较小,为了便捷,可直接忽视。一般来说,质心处侧倾轴上方位置。所以,车辆转向时,离心力作用在车身的时候,就会产生侧倾轴转动力矩,以此造成载荷发生位移,以出现侧倾。悬架两端弹簧保持在伸张与收缩状态,此时便会构成持衡于侧倾力矩的另一力矩[4]。即
(MΦf+MΦp)=zyWiki+WikiΦ
(1)
式中:MΦf与MΦp分别为前悬架与后悬架侧倾刚度,N/m;ki为质心与侧倾轴间距,m;zy为侧向加速度,m/s;Wi为车重,t;zyWiki为侧倾力矩,N·m;Φ代表侧倾角,(°)。
汽车转弯行驶时,车身侧倾,前轴与后轴车轮则会出现载荷位移。前轴车轮载荷位移量(ΔWf),基于力矩平衡关系,即
(2)
将式(1)代入式(2),即
(3)
式中:Q为前轴车轮中心线与后轴车轮中心线的间距,m;Qp为质心与前轴车轮中心线的间距,m;kf为前侧倾中心与地面间距;df为前轴车轮间距,m。
2.2 稳定杆力学分析
液压主动稳定杆等效机构,即曲柄滑块机构,具体如图3所示。

图3 等效机构
式中:曲柄OA即左右摆臂;AB即左右直拉杆;滑块即液压缸活塞杆,属于原动件。
滑块B虚位移εib水平向左时,曲柄OA出现虚位移εia。受AB连杆限制,A与B之间虚位移εia与εib处于连杆轴线的投影相等,否则连杆长度恒定的限制条件将会遭到破坏[5]。基于等效机构的几何关系,则
εiacos[90°-(α+β)]=εibcosβ
(4)
求解则
(5)
液压主动稳定杆系统受力模型[5]具体如图4所示。

图4 主动稳定杆受力模型
在车辆转弯行驶时,车身于H点作用于横向稳定杆,作用力即f,保持垂直向下的受力方向。
由于OA与OH之间处于刚性衔接状态,在作用力作用于H点的时候,则代表于OA增加了顺时针阻力矩,基于虚位移做虚功原理,则
F0εib=WΔα
(6)
车辆转弯行驶时,液压缸活塞杆开始面向左侧逐步位移,OA旋转角度为Δα,(°)。由于虚位移较小,并且A点相对O点以圆周运动,即
(7)
将式(4)与式(5)代入式(6),有
(8)
通过式(8)明确稳定杆输入力F与输出力f间表达式,在给定输出力值时,便可计算得出主动稳定杆系统所需液压缸提供力。
2.3 执行结构控制
稳定杆的位移量与反侧倾力矩间保持良好的线性关系,通过控制单元计算,获得车辆自身克服车身侧倾所需反侧倾力矩时,可明确液压缸推杆的目标位移量[6],即
(9)
基于Bang-Bang算法控制液压执行机构位移,明确输入变量(x),输出变量即电磁开关阀电信号(V1、V2)。为降低阀开关频率,将滞环宽度引进位移控制器,具体算法,即:
(10)
式中:V1/V2=12V代表电磁阀通电处于开启状态;V1/V2=0 V代表电磁阀断电处于关闭状态;Δ=0.001 5代表滞环宽带,m。
3 液压模型
基于AMEsim构建执行机构液压模型[7],具体如图5所示。

图5 液压模型
4 执行机构性能参数影响仿真分析
4.1 液压缸
以单活塞液压缸为例,其参数即缸筒内径与活塞杆外径。基于不同缸径与杆径实现批处理运算,仿真分析结果具体如图6、图7所示。

图6 推杆输出力曲线

图7 推杆速度曲线
由图6、图7可以看出,缸筒内径越大,则推杆进退速度就会越小,执行机构响应时间则越长。但是缸筒内径过小,受固定油压作用,受力面积小会直接造成输出作用力减小。推杆的进退速度过大,很容易引发脉动冲击,使得执行机构稳定性明显降低。而缸筒的内径相同情况下,推杆外径逐步变小,那么液压缸有杆腔和无杆腔之间的受力面积差距则会随之缩小,基于系统要求下,可以选择偏小推杆外径。
4.2 阀芯截流面积
基于主动稳定杆输出力矩与响应时间标准,电磁开关阀芯截流面积控制在3~7 mm2。为对截流面积的影响性进行全面检验,选择不同面积开展批处理运算,仿真分析[8]具体如图8与图9所示。

图8 不同截流面积下推杆输出力曲线

图9 不同截流面积下推杆速度曲线
由图9可以看出,截流面积越大,推杆进退速度越快,执行机构的响应速度则会随之加快。所以截流面积在很大程度上决定着液压回路液压油流动的速度。
4.3 软管内径
软管对于执行机构性能参数的影响主要分为内径与长度两部分,在稳定杆系统中,一般情况下内径约10 mm,长度约5 mm。不同内径下推杆输出力曲线具体如图10所示。

图10 不同内径下推杆输出力曲线
由图10可以看出,内径≤8 mm条件下,推杆输出力曲线存在显著性差异,据此内径小则软管管路流通性差,进而执行结构响应速度变慢。而内径>8 mm条件下,推杆输出力曲线处于大体重合状态,由此可知,内径此时状态已经满足主动稳定杆系统流通能力。
在内径10 mm条件下,不同长度下推杆输出力曲线具体如图11所示[9]。
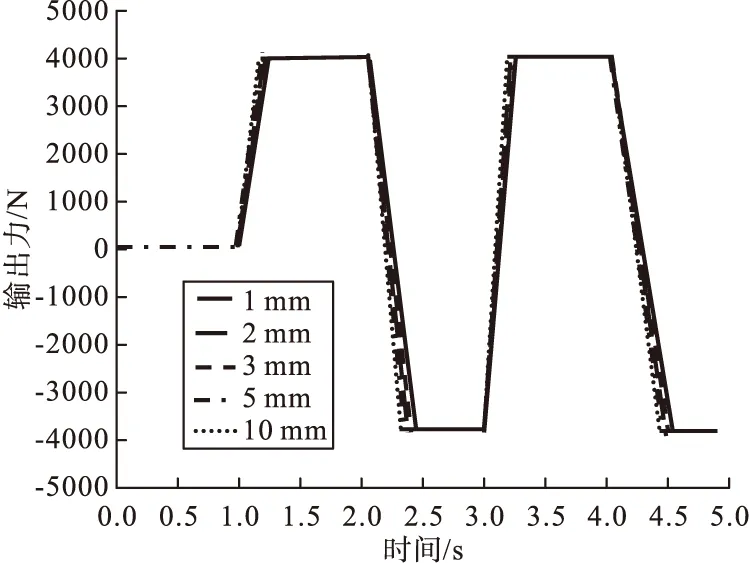
图11 不同长度下推杆输出力曲线
由图11可以看出,软管长度不同时,推杆输出力曲线大致重合,并不存在显著性差异,因此油压与内径保持恒定状态,则软管长度造成的主动稳定杆影响偏小,据此保障软管具体长度符合具体需求即可。
5 结 论
综上所述,通过AMEsim构建的液压系统模型,面向执行机构对其性能影响参数开展了深层探究分析。结果表明,液压模型可切实满足液压主动稳定杆系统性能指标要求;液压缸缸径与杆径、电磁开关阀芯截流面积、软管内径为执行机构性能的主要影响参数。在液压缸缸筒内径逐渐增大趋势下,机构响应速度减缓,其缸径与杆径在很大程度上决定了机构响应特征;电磁开关阀的通电与断电与液压缸推杆运行趋势、输出力息息相关,其开关阀芯截流面积对于液压回路油的流动速度发挥着直接的决定性作用;软管内径大小与也液压回路流通性密切相关,但是软管长度对于机构性能的影响非常小。
