基于拉曼光谱的已知混合物组分定量分析方法

颜 凡, 朱启兵*, 黄 敏, 刘财政, 雷泽民, 张 恒, 张丽文, 李 敏

1. 江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122 2. 北京卓立汉光仪器有限公司，北京 101102

引 言

近年来，基于拉曼光谱的检测分析方法由于具有无损、非接触、无化学污染、检测时间短、检测结果准确、重复性好、适用于大多数有机和无机化合物等优点，在微生物、法医分析，鉴定可卡因和其他非法药物的滥用、食品等领域得到了广泛的应用[1-3]。在利用拉曼光谱进行混合物组分的定量分析时，不同成分的光谱信号相互重叠，并且由于物质分子之间的相互作用导致它们的振动方式与纯物质相比有所不同，这给定量分析带来了很大困难。

檀兵等[4]利用Voigt函数对原始光谱进行拟合以解决多元素共存条件下的谱峰重叠问题；在此基础上，利用拟合谱峰的中心波长、光强、半峰全宽和谱峰质心构建特征参数向量，解决了传统谱峰识别方法难以提取谱峰波形形态特征导致的识别率难以保证的问题。

刘燕德等[5]利用600～3 000 cm-1波段的拉曼光谱，并结合支持向量机(SVM), 偏最小二乘(PLS)等定量分析模型分别对三组分食用调和油中各组分进行了快速定量检测，其中最优PLS模型的决定系数和RMSE分别为0.990 4和0.018 8。高颖等[6]利用非线性最小二乘法将天然气拉曼光谱分解为纯物质组分的拉曼光谱分量和若干个洛伦兹谱峰之和的形式，建立该组分特征峰面积和对应的浓度之间的模型。粟晖等[7]根据混合物光谱向量与其组分参考光谱向量二者间的空间向量夹角值与组分的相对含量存在线性关系，通过少量已知样本拟合出夹角值与其含量的标准曲线，实现混合物组分的定量分析。近年来，深度学习方法在光谱定量分析中的应用也得到了初步的应用。Fan等[8]提出了一种基于卷积神经网络(CNN)模型的混合物组分预测方法，得到了比传统建模方法更优的结果。Zhang等[9]提出了一种无需数据预处理的光谱定量分析方法，该方法利用一个由三个卷积层，一个平坦层，一个全连接层和一个输出层组成的卷积神经网络来进行组分定量分析，并报道了比传统卷积神经网络更优的结果。以上方法的预测精度与模型的建立好坏有直接联系，要取得较高的预测精度则需要大量的已知样本进行训练。然而不同组分构成的混合物模型也存在着差异，一旦测量环境和测量对象的组成发生改变，则需要重新收集样本建立分析模型，因此这类方法难以满足实际应用需要。

针对传统机器学习方法存在的训练样本难以获得，模型推广性能差的问题，本研究基于混合物拉曼光谱及其各组分的关系特性，提出了一种非学习的已知混合物组分的拉曼光谱定量分析方法，解决了传统建模方法需要大量已知样本并且模型不具有推广性等问题。

1 实验部分

1.1 仪器与样本

本研究的拉曼光谱数据由北京卓立汉光仪器有限公司的手持式拉曼光谱仪(Finder Edge)进行采集。其激发源为785 nm激光器，激光功率和积分时间可调，光谱范围为150～2 700 cm-1，光谱分辨率为8～10 cm-1。

本文采集了乙醇、乙腈、丙酮、环己烷、二丙酮醇、丙二酸二乙酯六种纯净物的拉曼光谱。利用这6种纯净物制备了十种不同类型的三元混合物，每种混合物样本依据其组分配置九种不同的体积比，共90个样本，表1为这6种纯净物构成的不同组分的三元混合物。

表1 十种不同类型的三元混合物Table 1 Ten different types of ternary mixtures

图1给出了这6种纯净物的原始拉曼光谱图。由于这6种物质在常温下都为无色的有机溶剂，具有相似的官能团，而拉曼光谱主要反应物质的分子结构，因此从图1中可以看出，任意两种物质的光谱都存在部分谱峰重叠的情况。

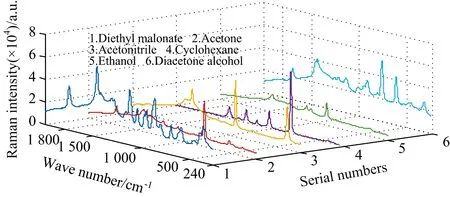
图1 手持拉曼光谱仪采集的六种纯净物的原始光谱Fig.1 The raw spectra of six substances obtained by a handheld Raman spectrometer

1.2 算法流程与原理

本文提出的基于拉曼光谱谱峰强度最小二乘拟合的已知混合物组分直接定量分析方法主要包括光谱预处理、拉曼光谱谱峰分解、和分解后谱峰线性表示求解三个主要环节。其主要步骤说明如下。

1.2.1 光谱预处理

由六种纯净物的拉曼光谱图1可知，峰位主要集中于240～2 000 cm-1区域内，因此选择该区域作为光谱区间。图2(a)为S1样本在九种不同体积比下的拉曼原始光谱图，从中可以看出，拉曼光谱仪采集的原始光谱含有较强的荧光背景，为了减少荧光背景对定量分析的干扰，本文采用连续小波变换和惩罚最小二乘法相结合的方法进行背景校正。图2(b)给出了背景校正后的拉曼光谱图，从图中可以看出，校正后的曲线消除了荧光背景产生的基线对物质拉曼光谱的影响，保留了光谱的有用信息。

1.2.2 拉曼光谱谱峰分解

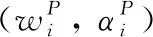
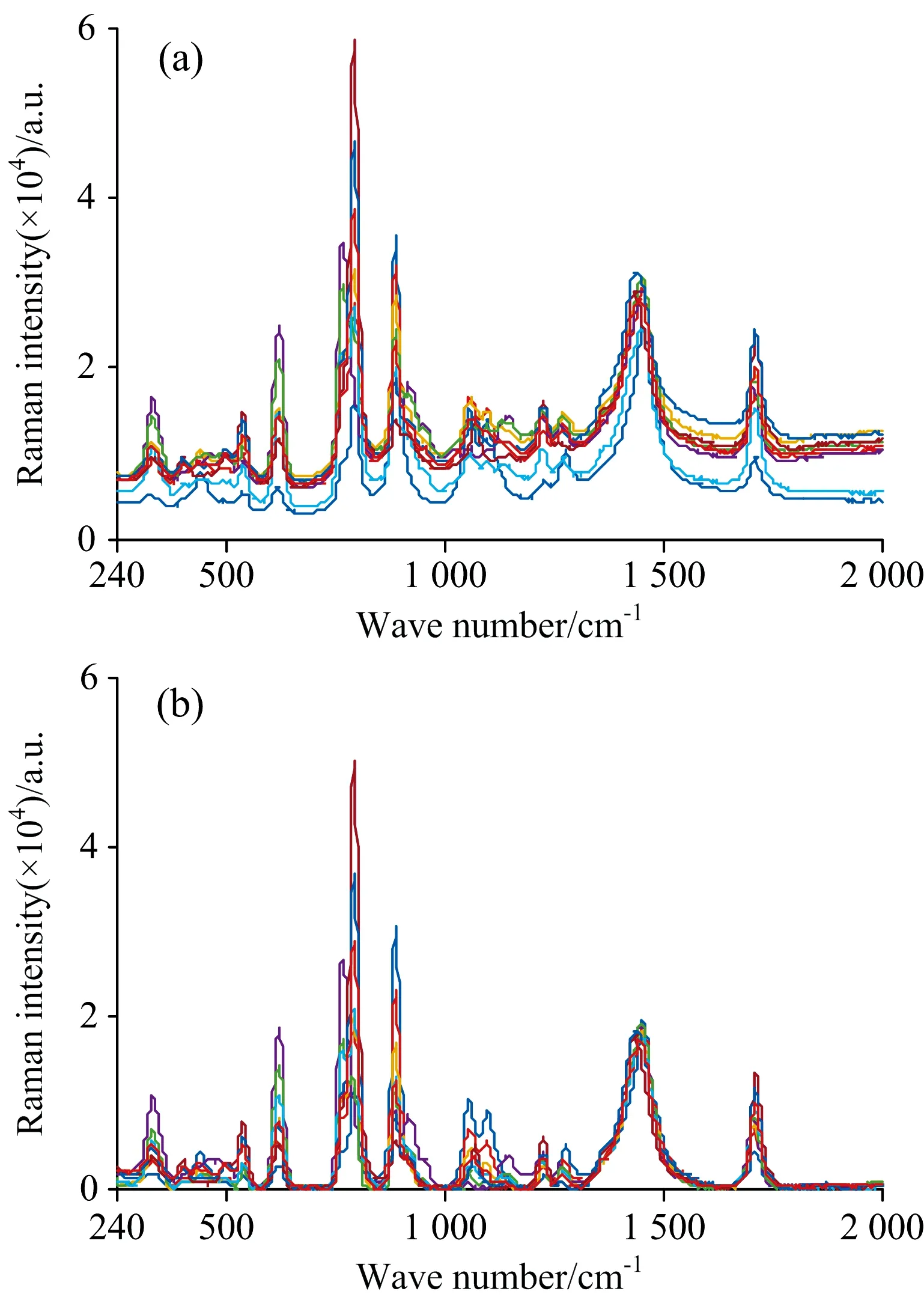
图2 (a)S1样本的拉曼原始光谱；(b)S1样本的预处理拉曼光谱Fig.2 (a) The raw Raman spectra of S1 sample；(b) The preprocess Raman spectra of S1 sample

拉曼光谱的谱峰形态本质上是洛伦兹线型，由于受仪器和被测样本自身特性的影响，实际测量得到的拉曼光谱谱峰波形通常可由Voigt函数来近似表达[11]

(1)

式(1)中，v为波数；α为谱峰强度；w为谱峰所对应的波数；γ为谱峰的半峰全宽；θ为高斯-洛伦兹系数，0≤θ≤1。对含有l个谱峰区域的光谱y进行解析，实际上就是对l个Voigt峰参数βi=(αi,wi,γi,θi), (i=1, …,l)进行拟合

r(v,x)=y(v)-f(v,x)

(2)

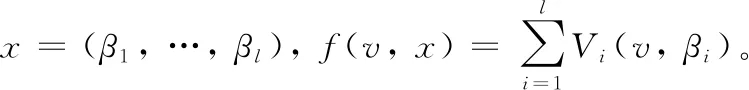
利用LMF算法对方程(2)进行求解。图4为利用LMF算法将光谱分解成单个Voigt峰的示意图，从图中可以看出，分解后的Voigt峰能准确反映各峰的形态。

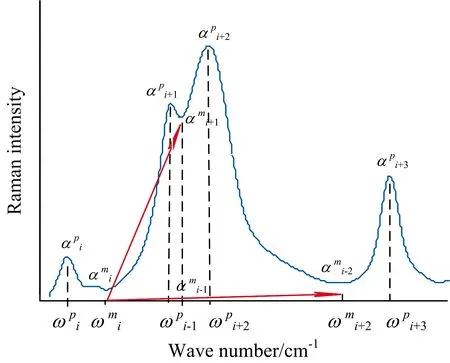
图3 区域划分示意图Fig.3 Schematic diagram of area division

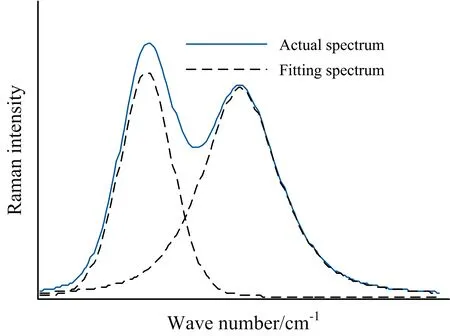
图4 基于Voigt的光谱分解示意图Fig.4 Schematic diagram of spectral decomposition based on Voigt

1.2.3 谱峰的线性表示与求解

对于分解为L个Voigt峰的三组分待测混合物光谱y，可得L个方程

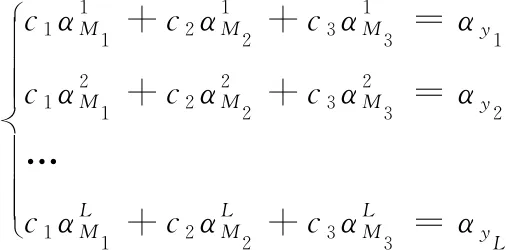
(3)

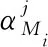
(4)

利用最小二乘法拟合方程(4)，获得组分系数，并对组分系数进行归一化处理，得到各组分的体积浓度。

1.3 算法评价指标

本文利用线性相关系数r、均方根误差RMSE和剩余预测偏差RPD作为算法的性能评价指标。其中r反应预测浓度与实际浓度之间的线性相关程度；RMSE反应预测值与真实值之间的偏差；RPD是真实值的标准差与均方根误差的比值，证明模型的预测能力，一般以RPD在2和2.5之间的值表示可以进行粗略的定量预测，而在2.5和3之间的值对应较好的预测精度，在3以上则表示极好的预测精度。

2 结果与讨论

2.1 数据处理

图5为纯净物乙醇、丙酮、环己烷以及由这三种组分构成的S3样本在V3(4∶3∶3)体积比混合下经过连续小波变换寻峰方法寻找到光谱的峰位并预估其谱峰特征参数，基于此作为LMF算法的输入进行拟合分解，峰位在图5中用空心圆标记，从中可以看到主要的峰位被完全找到，极少出现漏峰和伪峰的情况。图6为分解后的多个Voigt峰的叠加形式，每个独立的Voigt谱峰都可以由某种特定成分的分子振动所产生。例如，乙醇拉曼光谱分解后的主要特征峰的峰位882 cm-1(CC骨架伸缩)、1 052 cm-1(CC伸缩)、1 096 cm-1(CC伸缩)、1 247 cm-1(平面内变形)、1 453 cm-1(CH3CH2变形)，均能与原始峰位一一对应。从图6中可以看出，混合物S3-V3的每个Voigt谱峰均能与其三种组分的至少一个谱峰相对应。

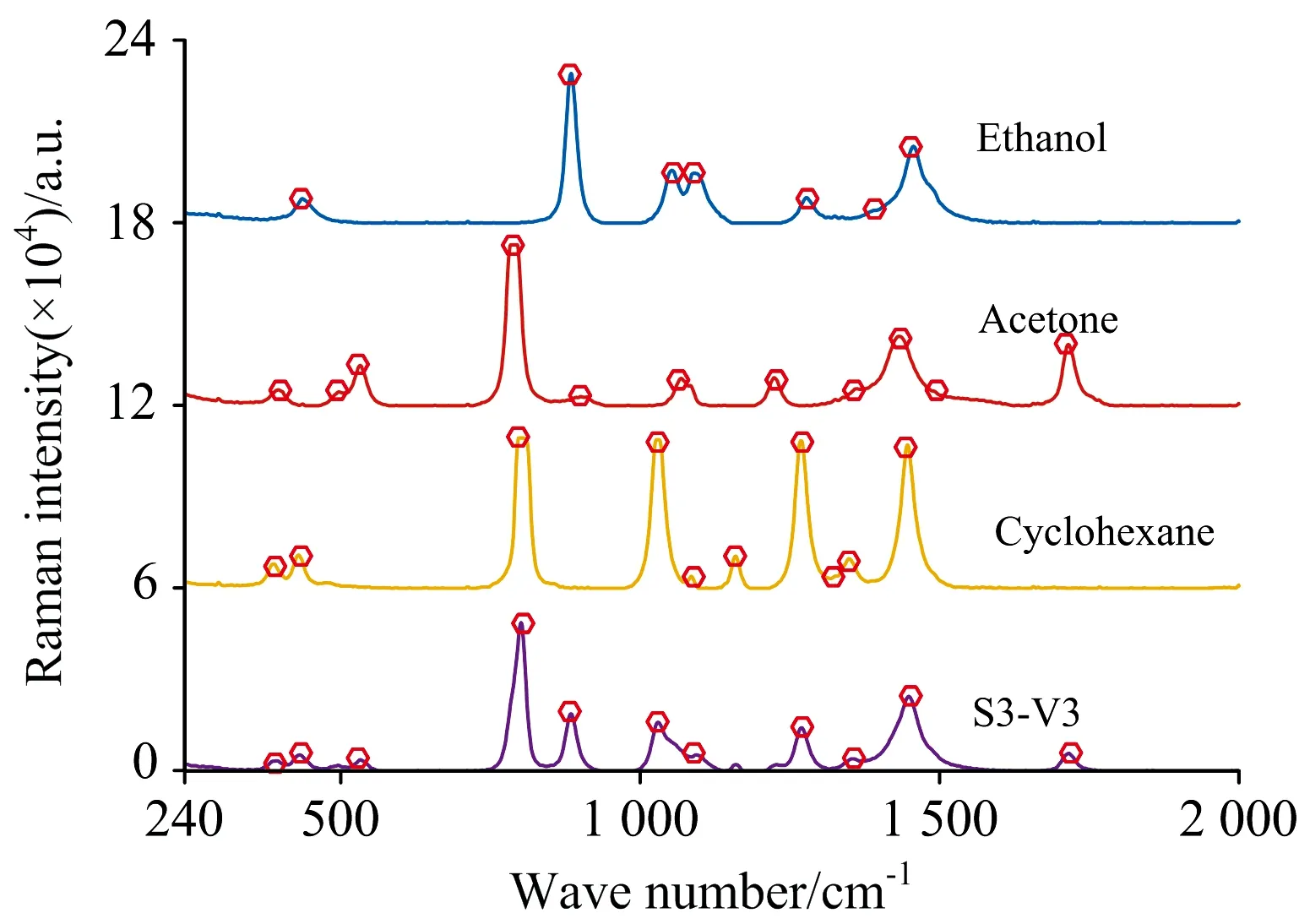
图5 乙醇、丙酮、环己烷和S3-V3的预处理光谱和峰位Fig.5 The preprocessed spectra and peaks of Ethanol, Acetone, Cyclohexane and S3-V3

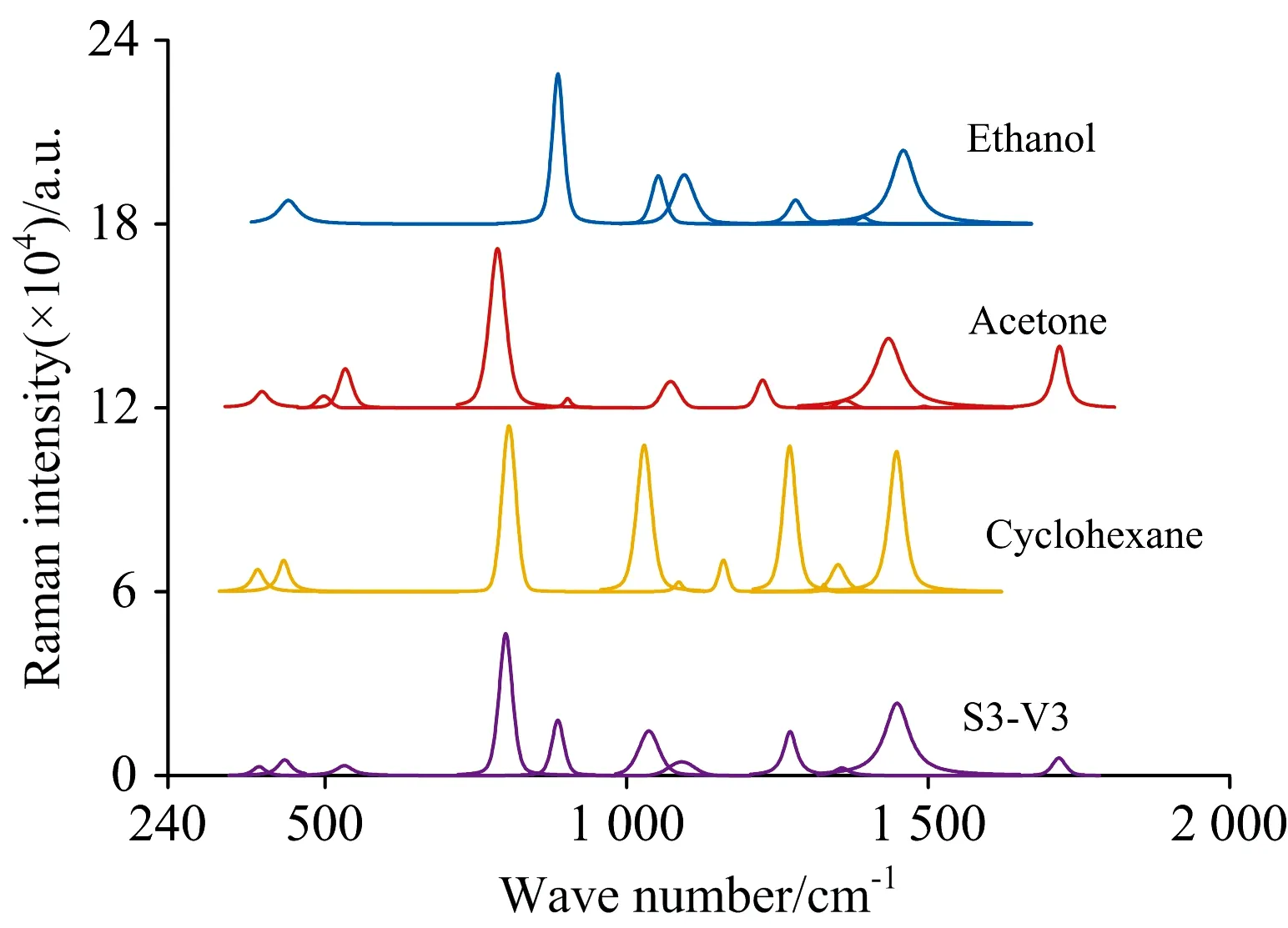
图6 基于Voigt的乙醇，丙酮，环己烷和S3-V3的分解光谱Fig.6 The spectra decomposition of Ethanol, Acetone,Cyclohexane and S3-V3 base on Voigt

2.2 混合物和其组分参考光谱同积分时间和功率下的识别结果

对于分解为L个Voigt峰的待测混合物样本，通过计算每种组分在混合物每个Voigt峰位光强的贡献值，依据朗伯-比尔定律中光强与其所占浓度的正比例关系，利用式(4)得到混合物各组分的体积浓度。采用本文提出的算法对混合物及其组分在同一积分时间和功率下的光谱进行定量分析，即选择表1的S1—S5共5种混合物(每种混合物各9个体积浓度比)，共45个样本。表2为根据组分划分的预测体积浓度与实际体积浓度的R，RMSE，RPD以及含有该组分的样本个数。从表2中可以发现，六种组分的预测结果相关系数均在0.95以上，均方根误差都小于6%，并且RPD指标仅乙醇相对较低，为2.921 5，其余五种组分RPD指标均在3.0以上。图7为6种组分的散点图，横轴为实际体积浓度，依据本研究选用的体积比，其取值为0.1，0.2，0.3，0.5和0.7，纵轴为通过算法预测的体积浓度比。从图中可以看出，六种组分的浓度与其拉曼谱峰光强都呈现较强的正相关。

表2 混合物和其组分参考光谱同积分时间和功率下的结果Table 2 The quantitative analysis results of the mixture and its component reference spectra under same integration time and power

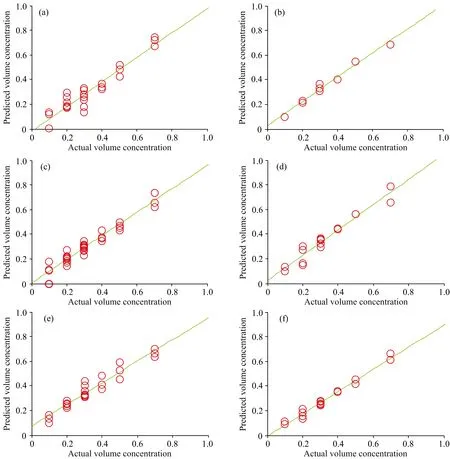
图7 预测体积浓度与实际体积浓度的散点图(a)：乙醇；(b)：乙腈；(c)：丙酮；(d)：环己烷；(e)：二丙酮醇；(f)：丙二酸二乙酯Fig.7 Scatter plot of predicted and actual volume concentrations(a)：Ethanol；(b)：Acetonitrile；(c)：Acetone；(d)：Cyclohexane；(e)：Diacetone alcohol；(f)：Diethyl malonate

2.3 混合物和其组分参考光谱不同积分时间和功率下的识别结果

在实际应用中，为了得到信噪比适当的混合物拉曼光谱数据，往往需要对拉曼光谱仪的功率或积分时间进行调整，从而导致混合物与各组分光谱测量条件的差异。为了验证算法的适应性，论文也对不同积分时间和功率下的混合物识别结果做了测试，即选择表1的S6—S10共5种混合物(每种混合物各9个体积浓度比)，共45个样本，组分的参考光谱统一选择光源功率300 mW和积分时间2 s。表3给出了具体的定量分析结果。由表3可知，六种组分的r均大于0.93，最大均方根误差为7.94%，除了组分乙醇、乙腈的RPD值小于2.5(分别为2.191 5和2.203 0)，其余4种组分的RPD值均接近或大于3.0，证明了该算法具有较强的鲁棒性。

表3 混合物和其组分参考光谱不同积分时间和功率下的定量分析结果Table 3 The quantitative analysis results of the mixture and its component reference spectra under different integration time and power

3 结 论

提出了一种基于拉曼光谱谱峰强度最小二乘拟合的混合物组分直接定量分析方法。为了验证算法的可行性，本研究配置了90个三元混合物样本，其中样本与其组分参考光谱同功率和积分时间下的45个，不同功率和积分时间下的45个。结果表明，在同功率和积分时间下，所有组分的相关系数都在0.95以上，均方根误差均小于6%，RPD最低为2.921 5，其余组分RPD指标均在3.0以上；在不同功率和积分时间下，所有组分的相关系数均大于0.93，最大均方根误差为7.94%，RPD指标相比同功率和积分时间下的略有下降，但仍大于2.0，满足混合物组分快速定量分析的要求，证明了该算法良好的鲁棒性，在实际应用中具有重要的价值。