改进的联合区间随机蛙跳算法的近红外光谱波长选择
2020-11-05程介虹陈争光
程介虹,陈争光,2*
1. 黑龙江八一农垦大学电气与信息学院,黑龙江 大庆 163319 2. 黑龙江省水稻生态育秧装置及全程机械化工程技术中心,黑龙江 大庆 163319
引 言
近红外光谱区(800~2 500 nm)的含氢基团的倍频和合频吸收峰组成的吸收强度较弱灵敏度较低,吸收带较宽且严重重叠。若采用全谱建模,不仅会存在某些光谱区域与待测组分相关性弱,而且相邻的波长高度相关,包含了大量的冗余信息,这都会影响模型的精度和稳健性。克服这些问题的有效途径是对所测得的光谱进行波长选择,减少建模所需的波长点和计算工作量,进而得到预测能力强、鲁棒性高的模型。在众多特征波长选择算法中,随机蛙跳(random frog, RF)[1]是近年来提出的一种新型特征波长选择算法。其依据不同的变量具有不同的被选择可能性,通过多次迭代,计算每个变量被选择的概率,选择概率高的变量为特征波长。
陈立旦等[2]通过RF选出特征波长后,建立最小二乘支持向量机(least squares support vector machine, LS-SVM)模型,对生物柴油的含水量进行预测,发现RF-LS-SVM模型的相关系数大于0.95,可以准确地预测生物柴油的含水量。胡孟晗等[3]通过RF对特征波长进行提取,建立LS-SVM模型预测蓝莓硬度和弹性模量,与全谱模型对比,RF算法可以有效地去除冗余信息,提升模型预测准确率。孙红等[4]采用相关系数法(correlation coefficient, CC)和RF算法筛选对叶绿素含量敏感的波长,建立偏最小二乘回归(partial least squares regression, PLSR)模型对马铃薯作物的叶绿素含量进行预测,结果表明RF-PLSR模型预测精度优于CC-PLSR,可实现马铃薯不同叶位叶绿素含量的无损检测。此外,Yu等[5]采用RF和PLSR建立校准模型,发现通过380~1 030 nm区域的波长可实现辣椒植物的总氮含量的预测。Zhao等[6]通过RF算法选择特征波长,建立RF-PLSR和RF-LS-SVM模型预测桑葚果实的总可溶性固体值含量,两个模型皆具有良好的性能。以上结果表明RF算法在数据降维方面是有效的。
尽管RF算法在特征波长选择方面具有一定优势,但存在两方面的不足:其一是,初始变量集V0的产生是随机的,难以保证初始信息的有效性;算法为保证运行过程中遍历整个数据集,要求迭代次数N需足够大,从而导致算法的运行时间长、收敛速度慢。其二是,RF在选择特征波长时,选择被选概率值大于阈值的变量为特征波长,但对阈值的设定无理论依据,易受人为因素影响。
针对上述两点,对RF算法进行了改进,提出一种联合区间随机蛙跳(synergy interval-random frog, Si-RF)算法,以一组公开的土壤样本近红外光谱数据为例,分别利用RF和改进的Si-RF进行特征波长选择,建立多元线性回归(multiple linear regression, MLR)模型,比较预测精度,并与全谱的PLSR模型进行对比,以证明改进的Si-RF算法的有效性。
1 实验部分
1.1 样本数据
所用数据为一组土壤样本近红外光谱数据,来自于网站Quality & Technology。该数据集包含108个土壤样本。样本光谱的波长范围为400~2 500 nm,采样间隔为2 nm,共计1 050个波长点。本文以土壤有机质(soil organic matter, SOM)的含量作为因变量进行波长选择及近红外光谱数据建模预测分析。
1.2 随机蛙跳算法
1.2.1 算法步骤
RF是Li[1]提出的一种类似于可逆跳跃马尔可夫链蒙特卡罗(reversible jump Markov Chain Monte Carlo, RJMCMC)的算法,它以迭代的方式进行,计算每个变量在每次迭代中被选择的概率,概率越高变量重要性越大,优选概率高的变量为特征变量。
随机蛙跳的主要步骤包括以下三步[1]:
(1)初始化:参数设置,随机选择一个包含Q个变量的变量子集V0;
(2)概率引导模型搜索:基于V0,选择包含Q*(随机产生)个变量的候选变量子集V*,以一定概率接受V*作为V1,并用V1代替V0,循环此步骤直至N次迭代完成;
(3)变量评估:计算每个变量被选择的概率,概率越高变量重要性越大。
其中概率引导模型搜索和变量评估具体方法如下。
1.2.2 概率引导模型搜索
首先,从均值为Q、方差为0.3Q的正态分布中随机选择一个整数Q*,之后通过以下三种方式之一产生一个包含Q*个变量的候选变量子集V*:
(1)如果Q*=Q,则令V*=V0。
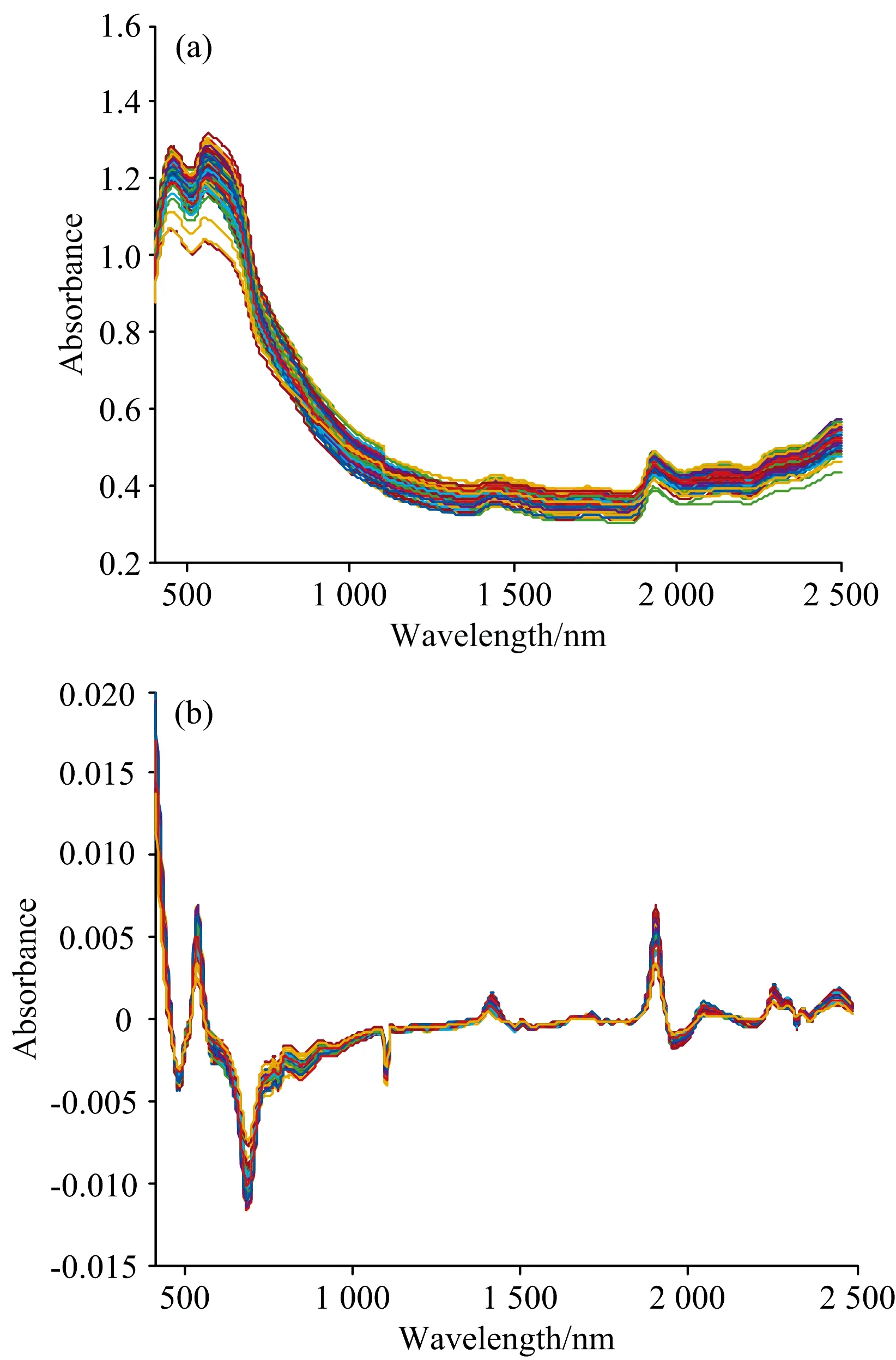
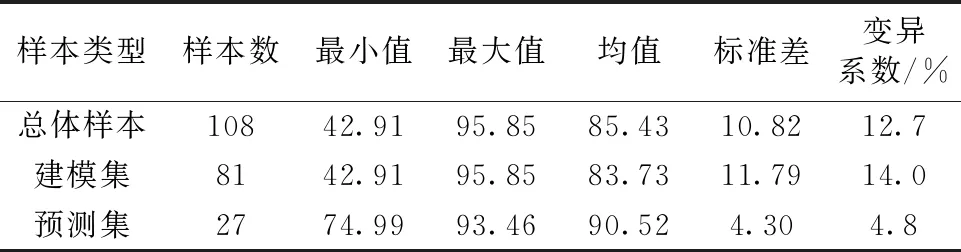
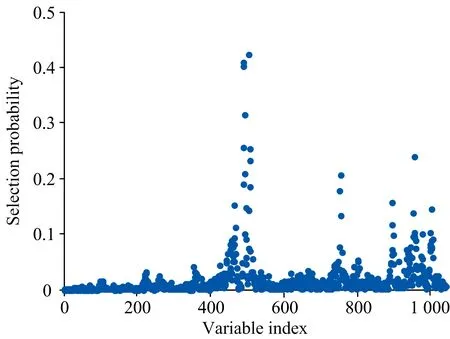
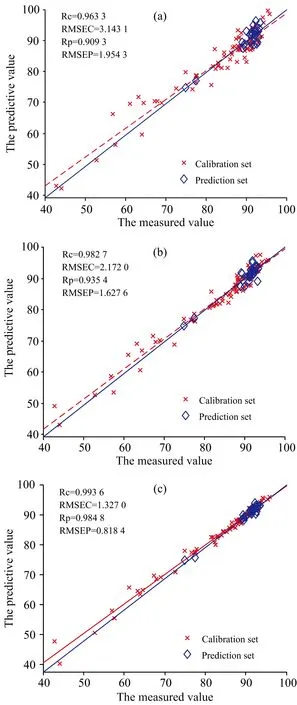
(2)如果Q* (3)如果Q*>Q,则从V-V0(V代表包含全部p个变量的集合)中随机抽取ω(Q*-Q)个变量,ω默认值为3,生成一个变量子集T,通过V0和T的组合建立PLS模型,保留模型中回归系数最大的Q*个变量,并将其设为候选子集V*。 简而言之,利用所提出的正态分布控制变量数,实现变量的增、删操作。在得到候选变量子集V*后,下一步是确定V*是否可以被接受。分别对V0和V*建立PLS模型,计算交叉验证均方根误差(cross-validation root mean square error, RMSECV),得到RMSECV和RMSECV*。如果RMSECV*≤RMSECV,接受V*为V1,否则接受V*为V1概率为0.1RMSECV/RMSECV*。最后,使用V1中的变量更新V0,并重复N次迭代,直至循环结束。 1.2.3 变量评估 N次迭代之后,总共获得N个变量子集。对于每个变量,可以使用式(1)计算其被选择的概率。 (1) 式(1)中,Nj为第j个变量在N次迭代中被选择的次数,变量越重要,被这N个变量子集选择的机会就越多。因此,该选择概率可以用作变量重要性的度量,可以用作变量选择的标准。 1.3.1V0子集的初选 在RF算法中,初始变量集V0的产生是随机的,具有较大的不确定性,可能会产生无信息变量或干扰信息,从而导致算法的迭代次数大,运行时间长。为了提高初始集V0变量的有效性,减少迭代次数,对V0子集的产生进行改进。 联合区间偏最小二乘法(synergy interval partial least squares, SiPLS)是Norgaard提出的一种波长选择算法。该方法将光谱划分为等宽的n个子区间,对其中m个子区间任意组合为联合区间。基于联合区间建立PLS模型,比较各PLS模型的RMSECV的值,将最小RMSECV值所对应的联合区间的波长设为初始变量集V0,开始迭代,可以消除V0的随机性,避免无信息变量及噪声的干扰,从而减少迭代次数。 1.3.2 建模波长的优选 在RF算法中,一般选择概率值较大的前10或15个变量,或者通过人为设定概率的阈值,取概率值大于阈值的变量来选择符合要求的特征波长,建模波长数量选择存在不确定性。 本文的改进是:对排序后的变量从第一个波长开始,每次增加一个波长,建立光谱数据和有机质含量数据之间的MLR模型。计算每个模型的验证均方根误差(root mean square error of validation, RMSEV)值,其中最小RMSEV值所对应的变量子集即为特征波长。RMSEV可以使用式(2)计算 (2) 这样可以找到预测精度最优所包含的波长数,提高预测精度。 现有研究大多对RF所选特征波长建立PLSR模型。而MLR是一种常规的校正方法,直观简单,且具有良好的统计特性,应用非常普遍,其优点是产生的模型比主成分回归(principal components regression, PCR)和PLSR模型更简单,更易于解释。 本工作建立三种模型:基于全谱的PLSR模型、基于RF波长选择的MLR模型和基于Si-RF改进的波长选择的MLR模型。通过三种模型预测能力的比较验证本法的有效性。模型的预测能力主要通过校正相关系数(Rc)、校正均方根误差(RMSEC)、预测相关系数(Rp)、预测均方根误差(RMSEP)指标来评价。其中,R取值越接近1,RMSEC和RMSEP越接近0,模型的拟合性越好,预测精度越高。 软件采用MATLAB R2015b及The Unscrambler X 10.3 (64-bit),光谱数据的预处理、建模分析及预测在Unscrambler软件中实现,特征波长提取、图形的绘制在MATLAB中实现。计算机硬件的配置为Intel(R)Core(TM)i5-3450CPU@3.50GHz处理器,8GB内存,操作系统为windows10。 土壤样本的原始近红外光谱图如图1(a)所示。为校正光谱基线,消除其他背景的干扰,提高光谱分辨率,并且在一定程度上减少各变量间的线性相关性,利用Savitzky-Golay窗口宽度为11的一阶求导法对原始光谱数据进行预处理,预处理后的近红外光谱图如图1(b)所示,可以发现通过预处理后的近红外光谱曲线,能更精确地确定吸收峰的位置。 图1 原始光谱图及预处理后的光谱图(a): 原始光谱图;(b): S-G一阶导处理后的光谱图Fig.1 Original and pre-processed spectra(a): Original; (b): S-G first derivative 将108个土壤样本通过SPXY(sample set portioning based on joint x-y distance)算法分为75%训练集和25%预测集,建模集包含81个样本,预测集包含27个样本,土壤有机质含量统计数据结果如表1所示。划分后的建模集的SOM含量范围涵盖预测集的SOM含量,建模集具有代表性。 表1 土壤有机质含量统计数据结果Table 1 Statistical data of soil organic matter content 2.2.1 RF变量选择结果 如前所述,首先对RF进行初始化参数设置,N设定为10 000,Q设定为10,开始运行。每个变量被选择的概率结果如图2所示,选择概率大于0.2的变量为最终特征波长,得到满足条件的有10个波长点分别为1 420,1 390,1 392,1 394,1 388,1 422,2 318,1 424,1 396和1 922 nm。 图2 RF运行结果Fig.2 The result of random frog 2.2.2 Si-RF变量选择结果 表2 SiPLS子区间优选结果Table 2 Sub-interval optimization results of SiPLS 由表2可以发现,将全谱等分为30个区间,组合数设置为3时,RMSECV最小,此时所选的特征波长点为104个,将这三个波段1 182~1 250,1 392~1 460和2 288~2 354 nm,共计104个波长点作为初始变量子集V0,RF算法的迭代次数分别设置为500,1 000,1 500和2 000次,得到结果如表3所示。 表3 不同迭代次数的优选结果Table 3 Optimal results of different iteration times 由表3可知,当N设置为1 000次时,RMSEV值最小。该情况下Si-RF运行结果如图3所示,每个变量被选择的概率结果如图3(a)所示。将每个变量被选择的概率值进行降序排列,从第一个波长开始,逐次增加一个波长建立MLR模型。各模型的RMSEV值如图3(b)所示,正方形标记所示为最低RMSEV值,为0.818 4,此时选择的特征波长数为17个,分别为1 392,1 394,1 420,2 332,2 330,1 418,1 440,1 348,1 920,1 402,2 000,1 424,2 312,1 442,1 426,1 444和2 364 nm。 图3 Si-RF运行结果(a): 各变量被选概率;(b): 各模型RMSEV值Fig.3 The result of Si-RF(a): Selection probability of each variable;(b): RMSEV values of each model 将全谱、RF以及 Si-RF选择的特征波长,建立回归模型比较预测能力,得到模型的校正、预测相关系数和校正、预测均方根误差的值如表4所示。 表4 不同波长选择方法下模型的结果Table 4 Results of model with different wavelength selection methods 从表4可以看出,RF和Si-RF模型的各项参数均优于全谱,改进的Si-RF算法模型的各项参数均优于RF。基于RF所选特征波长的MLR模型的Rp为0.9354,RMSEP为1.627 6,而改进后Si-RF选择的特征波长MLR模型的Rp为0.984 8,RMSEP减小到0.818 4,大大提升了预测精度。 图4分别为对建模集、预测集样本的全谱-PLS、RF-MLR和Si-RF-MLR模型的SOM的实测值和预测值相关图。从图中可以更加直观的看出,基于Si-RF波长选择算法的MLR模型优于全谱模型及RF算法的MLR模型。 图4 不同模型下土壤有机质的实测值和预测值相关图(a): 全谱-PLS;(b): RF-MLR;(c): Si-RF-MLRFig.4 Correlation between measured and predicted values of SOM obtained from different models(a): Full spectrum PLS; (b): RF-MLR; (c): Si-RF-MLR 由于RF算法对初始变量集的产生是随机的,有较大的不确定性,可能会包含无信息变量或干扰信息,从而导致算法的迭代次数大、运行时间长。而通过SiPLS特征波长初选,得到的波长对于目标变量变化最为敏感,同时避免了其他光谱无信息变量与噪声的影响。所以首先对全谱通过SiPLS进行特征波长初选,将其初选结果作为RF的初始变量子集V0,这样可以改善RF收敛速度慢的问题,减少RF算法的迭代次数,大大节省运行时间,并且由于初始变量子集是针对于有效信息的波长,有利于RF每次迭代中V*所包含的波长的选择,可以提高预测精度。在运行中,迭代次数也由10 000次减少至1 000次,提高运行效率。 通过Si-RF选出的特征波长点的范围在1 348~1 444,1 920~2 364 nm之间,这与许多前人研究所选波长点范围基本一致。如:白婷等[7]针对艾比湖60个表层土样,基于CARS算法提取的SOM特征波段主要集中在1 970和2 340 nm附近;朱亚星等[8]通过UVE-CARS优选出84个变量做为预测SOM含量的特征波长,分布于561~721和1 920~2 280 nm波段;于雷等[9]通过CARS-SPA优选出的37个特征波长,集中在近红外区域1 800~2 400 nm,而且基于波长选择建立的SOM含量的PLSR模型预测精度最优。本工作Si-RF优选出的波段与图2B近红外光谱曲线吸收峰的位置也基本一致,符合高志海等[10]的论点,即光谱曲线上的凸起区可能对提取土壤有机质信息有实际意义。 对比RF及Si-RF所选波长点范围,RF的范围在1 388~1 424和1 922~2 318 nm之间,Si-RF的范围在1 348~1 444和1 920~2 364 nm之间,可以发现Si-RF已经基本涵盖RF所选波长的大部分,这也在一定程度上说明可以减少算法迭代次数。 提出了一种近红外光谱分析中特征波长选择的Si-RF算法,该方法通过对全谱进行SiPLS特征波长初选,将所得的波长做为初始变量子集,使得初始变量子集涵盖有效信息,以解决RF中迭代次数过多,运行效率较低的问题。将RF和改进的Si-RF应用于一组土壤样本近红外光谱数据集,将由RF选择的特征波长和改进的Si-RF选择的特征波长提取出来,建立MLR模型,发现Si-RF-MLR模型的预测精度优于RF-MLR,并且在运行时间上也大大降低,提高运行效率;相较于全谱的PLSR模型,也极大的提高了预测精度,简化模型的复杂度。证明改进的Si-RF是一种有效的特征波长选择算法。1.3 对RF算法的改进
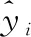
1.4 建模方法
1.5 数据分析
2 结果与讨论
2.1 光谱数据特征
2.2 特征波长选取
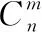
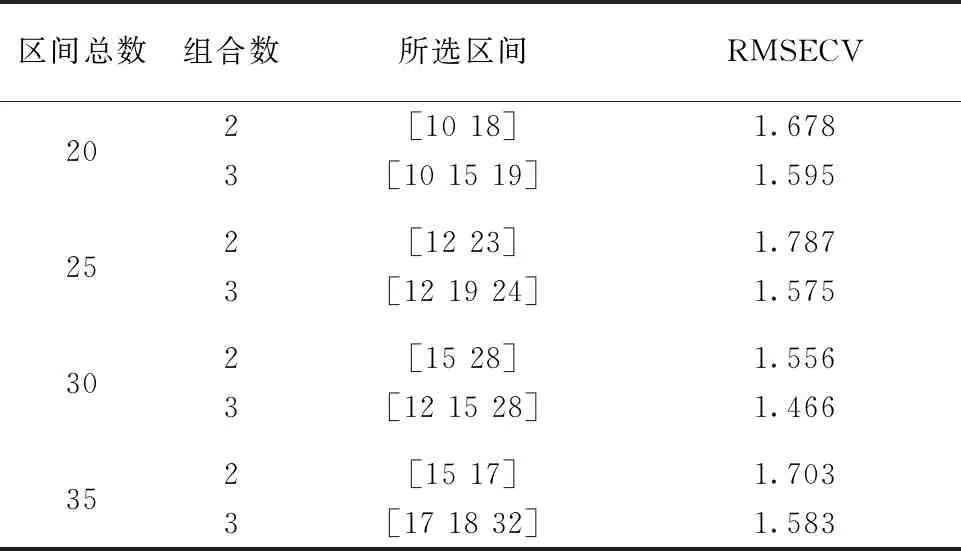

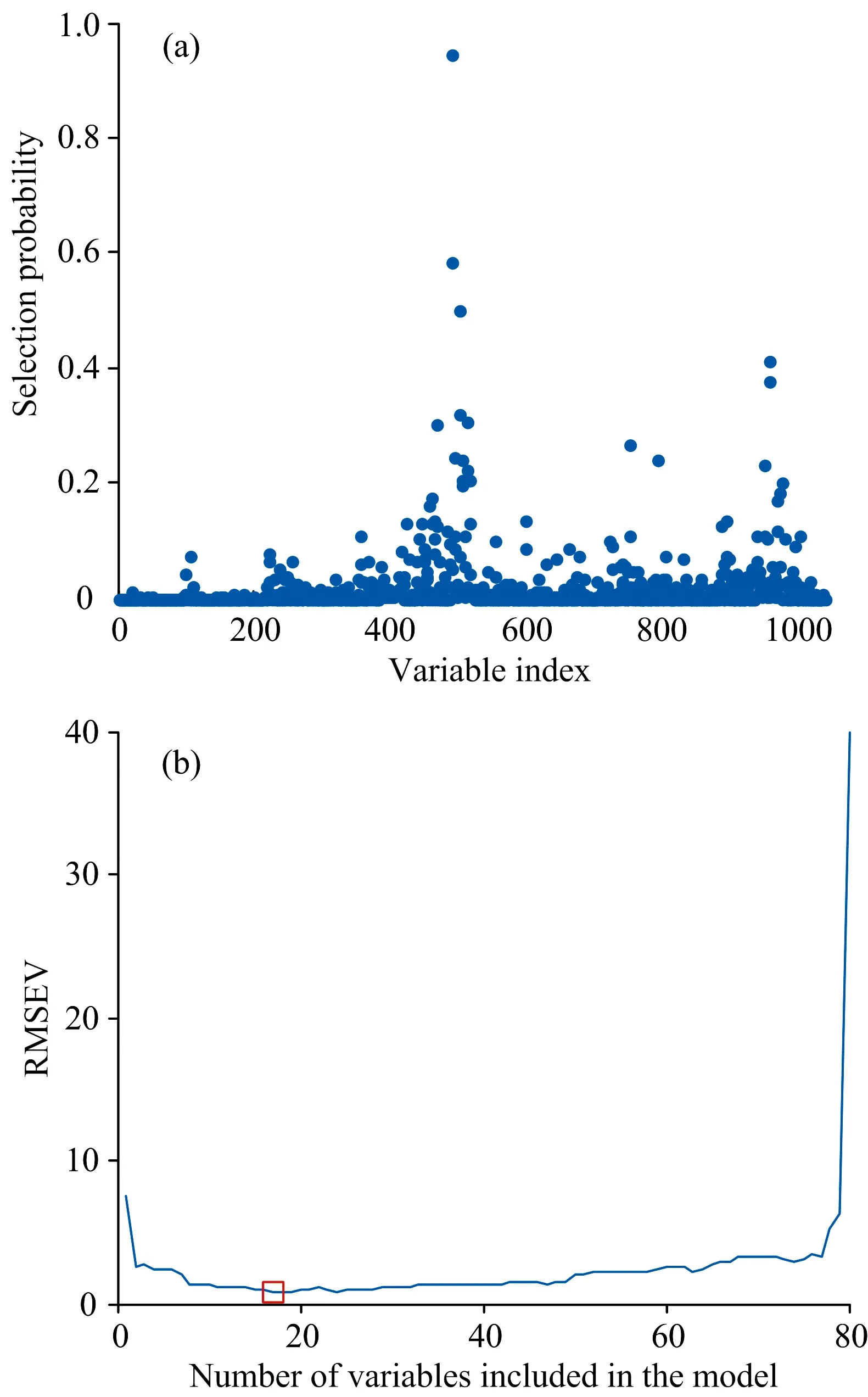
2.3 模型建立与比较
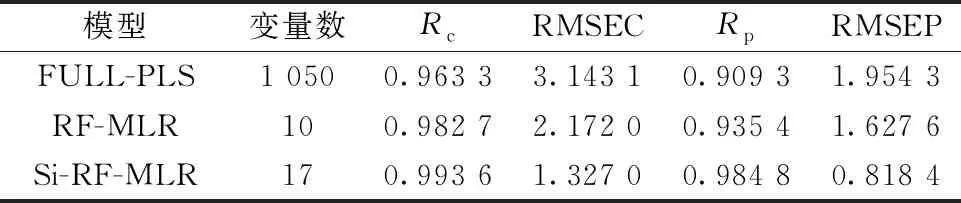
3 结 论
