海盗船立柱刚柔耦合动力学仿真分析

赵九峰

(河南省特种设备安全检测研究院，河南 郑州 450000)

0 引言

游乐设施的结构强度直接影响着乘客的生命安全，静力分析只能分析某个时间点的应力强度，而刚柔耦合动力学分析能够计算整个运行周期内的应力[1]，从而找出最大应力值，确保游乐设施的安全。

游乐设施的刚柔耦合分析当前普遍采用ANSYS软件和ADAMS软件的联合仿真，创建柔性体的模态中性文件，通过ANSYS软件和ADAMS软件之间的双向数据交换来完成刚柔耦合动力学分析[2]。随着仿真技术的不断进步，刚柔耦合动力学分析可以在ANSYS的仿真平台Workbench软件的瞬态动力学分析模块Transient Structural中实现[3]。

海盗船立柱受到船体摆动产生的载荷，随着摆角不断变化(包括载荷大小和方向变化)，通常认为立柱受到最大载荷时的工况为最危险工况。为了准确地模拟出立柱部件的最危险工况，本文基于ANSYS Workbench软件平台对其进行刚柔耦合瞬态动力学仿真分析。

1 海盗船运行原理和载荷分析

1.1 海盗船结构及运行原理

海盗船是一种观览车类游艺机，是一种绕水平轴往复摆动的游乐项目。“海盗船”因为其外形仿古代海盗船而得名，主要由立柱部件、悬臂部件、船体部件、驱动部件和站台护栏等部件组成[4]，设备简图如图1所示。

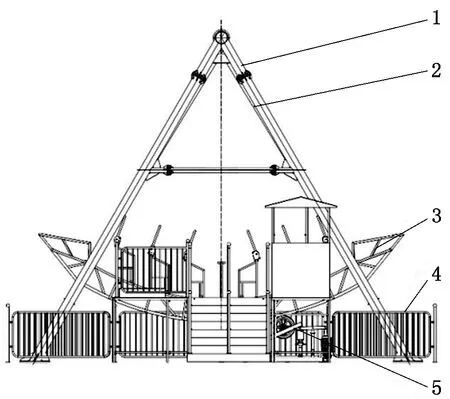
1-立柱部件；2-悬臂部件；3-船体部件；4-站台护栏；5-驱动部件

船体通过悬臂悬挂在立柱横梁吊耳上，座椅沿船体骨架布置，船体及立柱由型钢焊接和螺栓连接而成。乘客由站台上的客梯上船，坐在座位上将安全挡杆压到合适的位置。驱动部件主要由电动机、皮带轮、驱动轮胎组成，通过轮胎与船体底部周期性的摩擦驱动，驱动船体不断向上摆动。启动后从缓慢摆动到急速摆动，犹如乘客乘船出海遇到大风骇浪，海盗船时而冲上浪涛之颠，时而跌落波澜的谷底，既有趣又刺激，深受乘客喜爱。

1.2 载荷分析

海盗船工作时承受的载荷主要来自船体的摆动，每隔一定周期，轮胎驱动一次船体底部，在周期性的驱动力矩作用下，船体的向上位移不断增大，当摆角达到设计要求时，不再施加驱动力，船体部件做往复摆动。把整个船体和乘人做质点考虑，载荷示意图如图2所示。

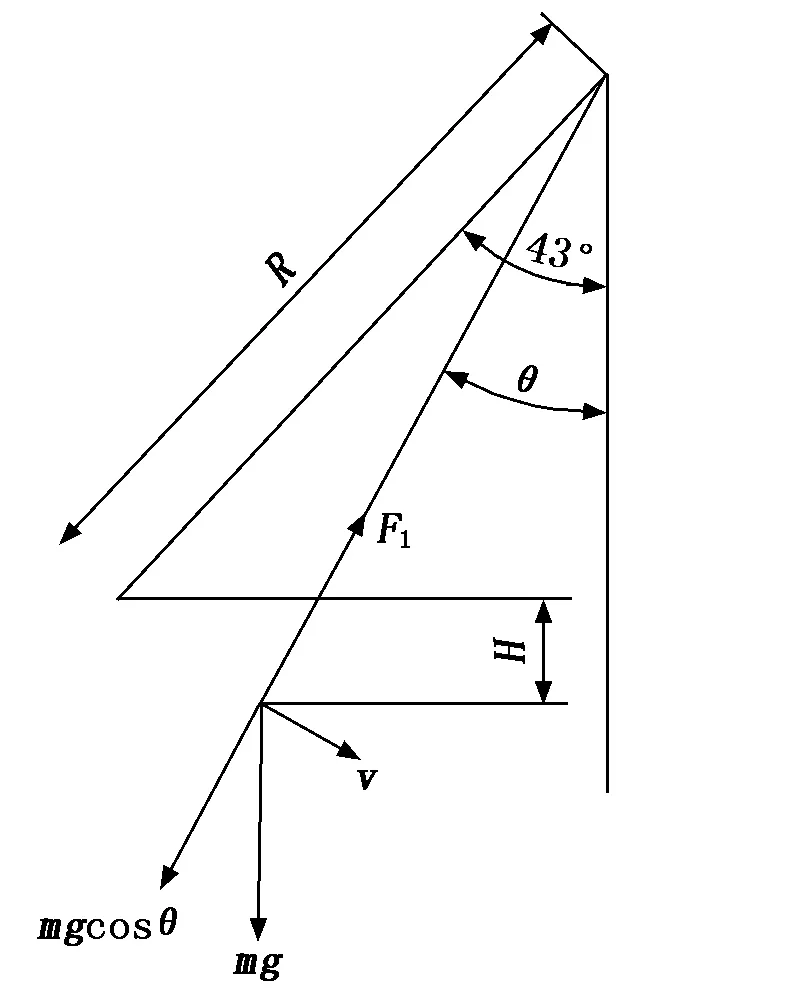
图2 海盗船运行载荷示意图

以24座海盗船为计算对象，海盗船的质心回转半径R=5.0 m，最大摆角θ=43°，摆动部件的质量m=5 000 kg(包括船体部件、悬臂部件和满载乘人质量)。立柱是由Φ219 mm×8 mm大直径无缝钢管(材料为20钢，抗拉强度σb=410 MPa)通过焊接和法兰螺栓连接而成的钢架结构。

船体从最高点下落过程中，由三角函数可得下落高度H(m)：

H=R(cosθ-cos43°).

(1)

下落过程中，整个系统仅受到重力的作用，根据机械能守恒[5]得：

(2)

其中：g为标准重力加速度，g=9.8 m/s2；v为海盗船摆动方向的瞬时线速度，m/s。

海盗船在摆动过程中绕着悬臂轴承连接轴中心线做圆周运动，圆周运动的向心力为F0(N)：

(3)

沿悬臂中心线方向上，摆动部分受到重力和悬臂的拉力，合力等于F0(N)，即：

F0=F1-mgcosθ.

(4)

其中：F1为悬臂的拉力，N。

联立式(1)～式(4)可得：

F1=mg(3cosθ-2cos43°).

(5)

由式(5)可知，海盗船立柱受到的悬臂拉力随着船体摆动角度的变化而变化。当摆角=0°，即船体运动到最低点时，受到(3cosθ-2cos43°)g=1.537g的加速度，属于物理学中的超重现象，重力势能全部转化为动能[5]，支架部件受到的载荷最大。

代入数据到公式(5)可得悬臂的最大拉力：

F1=5 000×9.8×(3cosθ-2cos43°)=75 327 N.

最大的摆动线速度为最低点时的瞬时速度，由公式(2)可得：

(6)

2 静力学分析

海盗船立柱为钢结构，取钢材的弹性模量为2.06×1011N/m2，钢材的密度为7 850 kg/m3，泊松比为0.3，采用4节点的壳单元(Shell181)，并使用四边形为主的网格划分，建立的海盗船立柱有限元模型如图3所示。立柱底部固定在基础上，故底部施加固定约束(Fixed)。按照上节计算的最大载荷施加到支架部件上，即悬臂吊耳部位施加75 327 N的向下拉力，考虑自重的影响，整体施加9.8 m/s2的向下重力加速度，载荷与约束如图4所示。

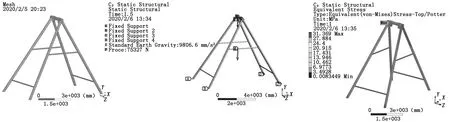
图3 海盗船立柱有限元模型 图4 海盗船立柱载荷与约束 图5 海盗船立柱应力云图

3 刚柔耦合动力学分析

3.1 模型与载荷

海盗船立柱组件通过悬臂与船体相连，船体做往复摆动，海盗船摆动一次为2.6 s。使用通用结构分析软件ANSYS Workbench，用Transient Structural模块对海盗船进行刚柔耦合的瞬态动力学分析，其中立柱部件采用柔性体建模，悬臂和船体组件采用刚性体建模。悬臂上部与立柱横梁吊耳部位施加旋转约束(Revolute)，座椅和乘人等转化为质量载荷，附加在船体上。仅在重力作用下，船体由摆角43°位置摆动下来，载荷与约束如图6所示。

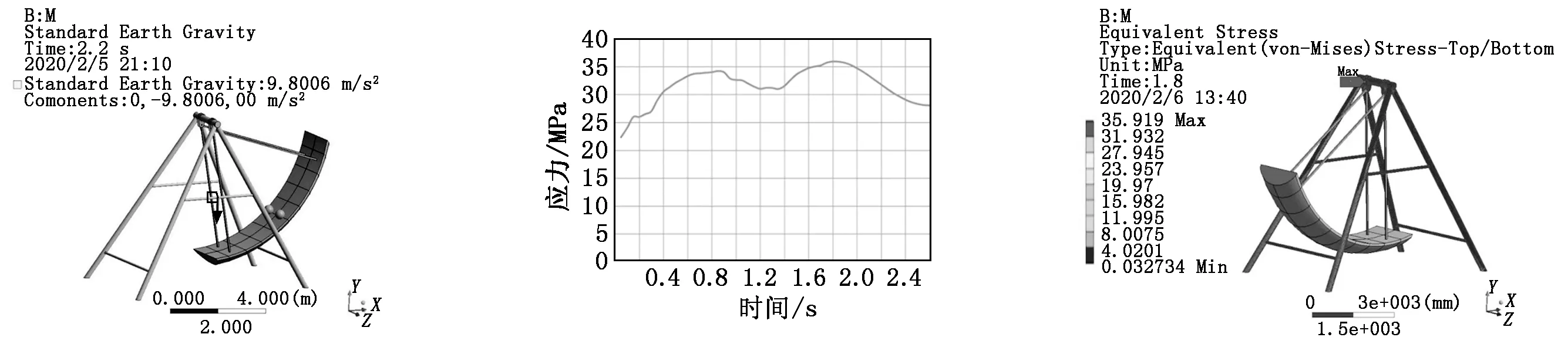
图6 刚柔耦合的动力学模型与载荷 图7 立柱最大应力-时间历程曲线 图8 1.8 s时立柱应力云图

3.2 结果与后处理

定义仿真分析时间为2.6 s，最小时间步为0.02 s，经过仿真分析，得到立柱在运动过程中的最大应力-时间历程曲线，如图7所示。从图7中可以看出，应力出现两个峰值，分别对应船体摆动到两侧立柱附近，摆角θ=0°时，应力值对应最大应力-时间历程曲线两个峰值之间的谷底，表明立柱在最大载荷作用下的计算应力不是摆动过程中的最大应力。

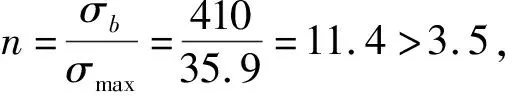
海盗船的最大摆动线速度为4.9 m/s，与理论计算的最大速度5.1 m/s误差约4%，速度-时间历程曲线如图9所示。立柱横梁受到的载荷为75 250 N，与理论计算的最大载荷75 327 N误差约0.1%，反作用力-时间历程曲线如图10所示。分析结果表明了刚柔耦合的动力学仿真过程、运动状态的正确性[7]。

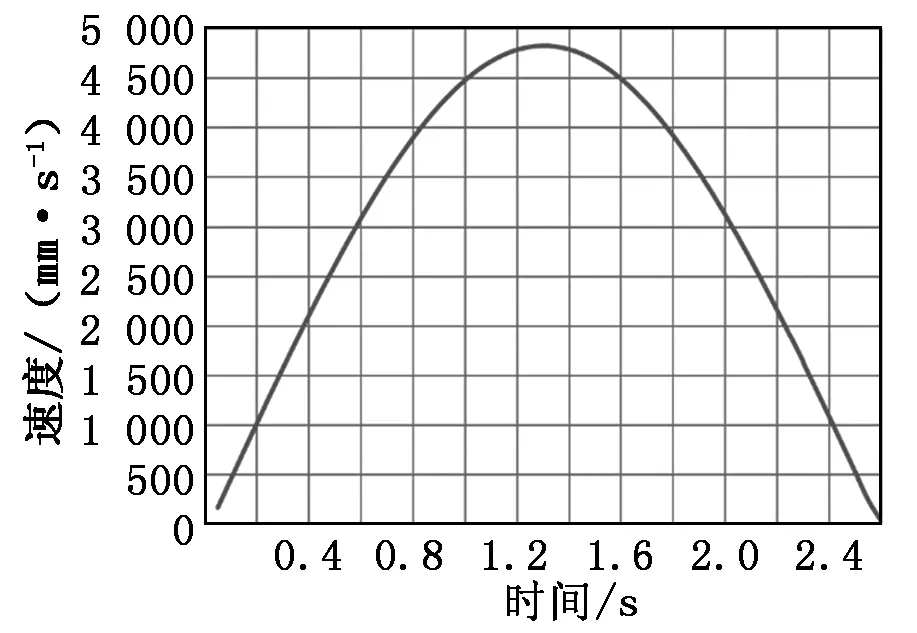
图9 速度-时间历程曲线

图10 反作用力-时间历程曲线

4 结论

本文以24座海盗船为工程背景，通过理论计算和仿真模拟，对海盗船立柱进行静力学分析和刚柔耦合的动力学分析，并对分析结果进行比较，算例未考虑风载荷、偏载和冲击系数等因素的影响[8]。计算结果表明：

(1)通过力学理论分析可知，海盗船立柱受到的载荷随着摆角变化而变化，海盗船摆动到最低点时，立柱受到的载荷最大。

(2)立柱在最大载荷作用下的计算应力并不是立柱摆动过程中的最大应力，立柱的最危险工况不仅与载荷的大小有关，还与载荷的方向有关；在仿真分析时，如果利用最大载荷去进行静力学分析，结果的准确性会降低，不能准确地反映立柱应力强度的真实特性。

(3)通过本文对海盗船立柱的刚柔耦合动力学分析，设计者可得到海盗船立柱在整个摆动周期内的最大应力，对海盗船的立柱的最危险工况有较为准确的了解。

本文运用有限元软件ANSYS Workbench对海盗船立柱进行刚柔耦合的动力学分析，避免了分析数据在不同分析软件之间的相互交换，其计算方法和结果可为游乐设施结构应力计算和校核评价提供参考，对于提高设计能力具有现实意义。