锥形件强旋成形有限元建模关键技术研究*
2020-11-05张晋辉谢瑞珍
张晋辉,牛 婷,温 凯,谢瑞珍
(晋中学院 机械学院,山西 晋中 030619)
0 引言
LF2M属于典型的Al-Mg系防锈铝合金,由于具有比强度高、耐磨性高、抗蚀性好、疲劳性能良好等优点,已广泛应用于航空航天、武器装备、石油化工等领域的重要部件中[1]。锥形件强旋是一个多因素交互作用下的复杂的局部连续塑性成形过程[2],在实际生产中工艺参数的选择主要依据经验而定,同时该成形工艺的复杂性加深了仿真模拟的难度。本文根据具体的锥形件强旋变形特点[3-4],在对建模过程涉及到的关键技术进行探讨与处理的基础上,建立了可靠的符合实际的三维有限元模型,进而为锥形件旋压成形的工艺试验研究与参数确定及优化提供了有效的参考。
1 锥形件强旋成形有限元建模的关键技术
1.1 锥形件强旋成形几何模型
本文研究的锥形件坯料外径D0=100 mm,内径D0′=20 mm,厚度t0=3 mm;旋轮圆角半径r=6 mm,直径Dρ=80 mm,锥角β=45°,宽度B=25 mm,进给比f=1.8 mm/r;芯模小端直径D1=40 mm,大端直径D2=160 mm,圆角半径R=6 mm,锥角α=45°,转速n=195 r/min。
为了使建立的三维模型简单适用,采用Tie方式将毛坯与芯模固定在一起,实现芯模与毛坯的完全同速运转,从而避免了尾顶的建模工作;采用双旋轮装置,旋轮对称分布,旋轮沿芯模母线方向进给。建立的锥形件强旋成形三维模型如图1所示。
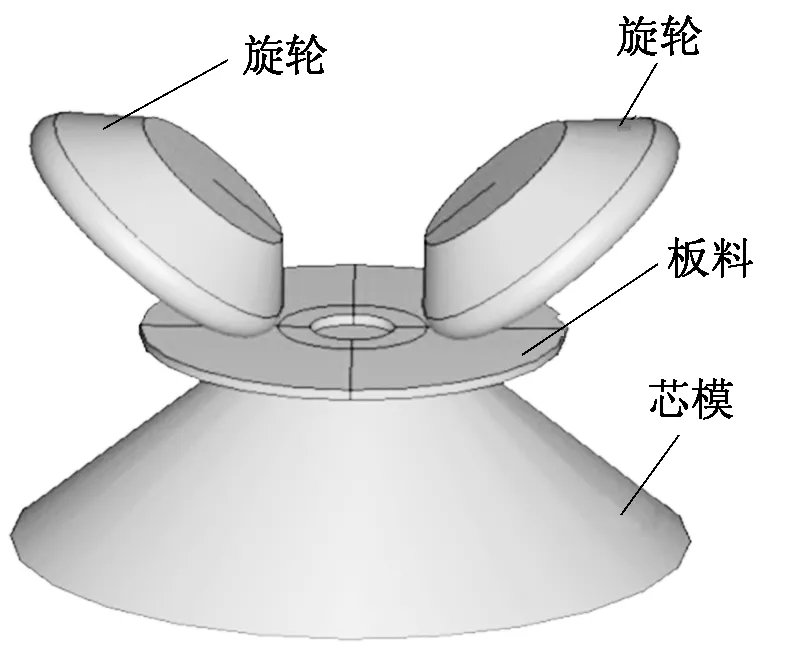
图1 锥形件强旋成形三维模型
1.2 材料属性设置

1.3 单元选取
芯模采用离散刚体,旋轮采用解析刚体进行处理,以减少模拟的仿真运算量和计算模拟时间。由于线性减缩积分单元能够很好地承受扭曲变形,故毛坯采用六面体显式线性减缩积分实体单元C3D8R进行离散。为了便于模拟过程中有关应力应变等场变量的输出和处理,在模型中定义了坯料的局部材料方向,即局部材料方向是随着板料的变形而转动的,因此定义变形后1方向为坯料母线方向,2方向为坯料周向,3方向为坯料法向,如图2所示。
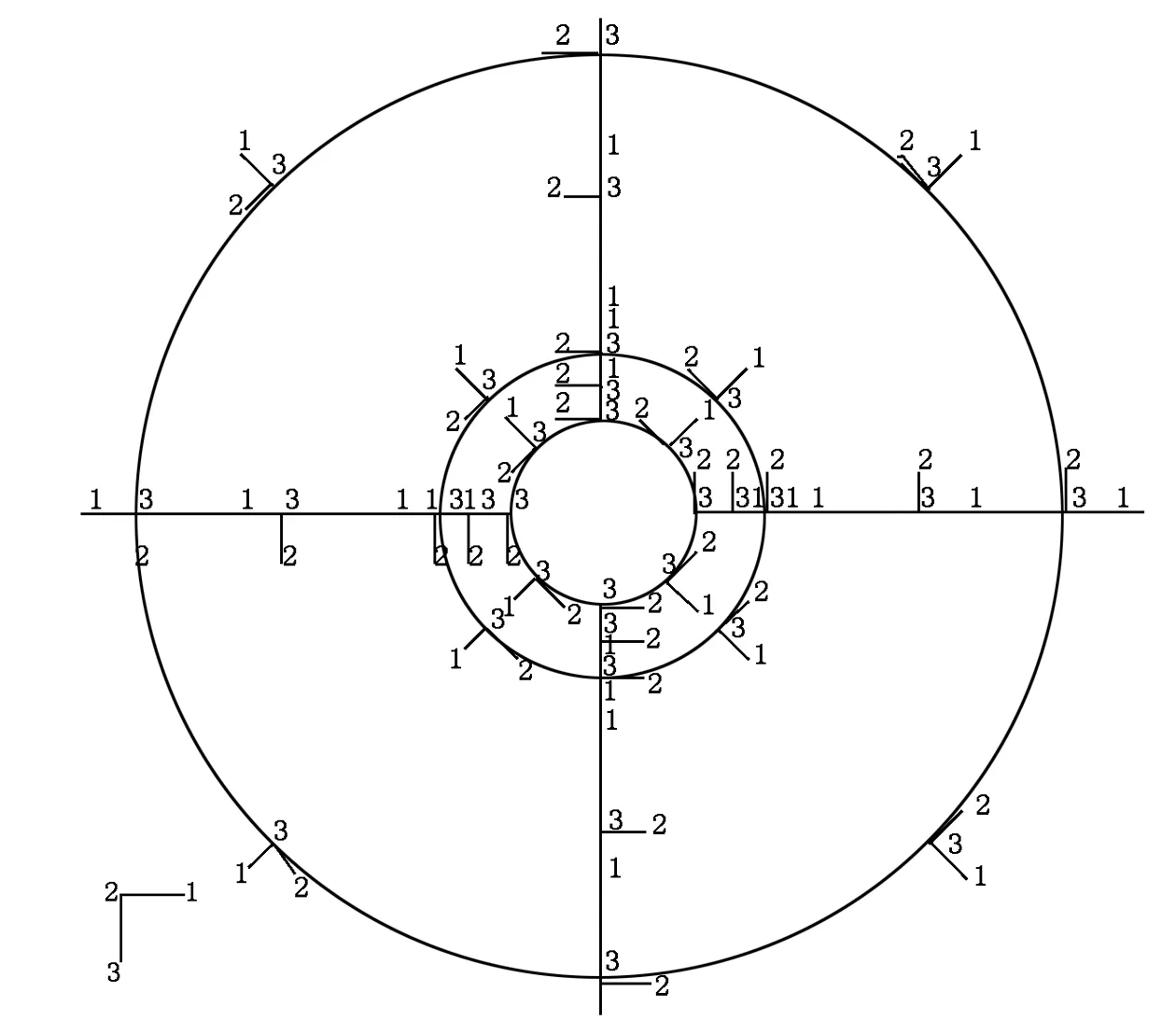
图2 坯料局部材料方向定义
1.4 网格划分
本文采用各向同性材料,考虑到数值模拟的精确性和模拟的效率问题,对坯料、芯模以及旋轮采用不同的单元进行不同密度的网格划分。在ABAQUS软件中,坯料采用实体单元C3D8R进行离散,为了模拟的精确性,对坯料进行网格局部细化,在径向、轴向壁厚和同向进行单元网格划分,整个工件共划分为6 600个单元、9 200个节点。对于芯模和旋轮,由于在旋压过程中理想的情况被认为是不发生变形的,因此假设成刚体,网格的密度也相应地比坯料要小得多,以提高计算效率。其中芯模视为R3D4壳单元刚体进行离散,共802个单元、824个节点;旋轮视为解析刚体进行离散,无需网格的划分。坯料和芯模的单元网格划分分别如图3、图4所示。
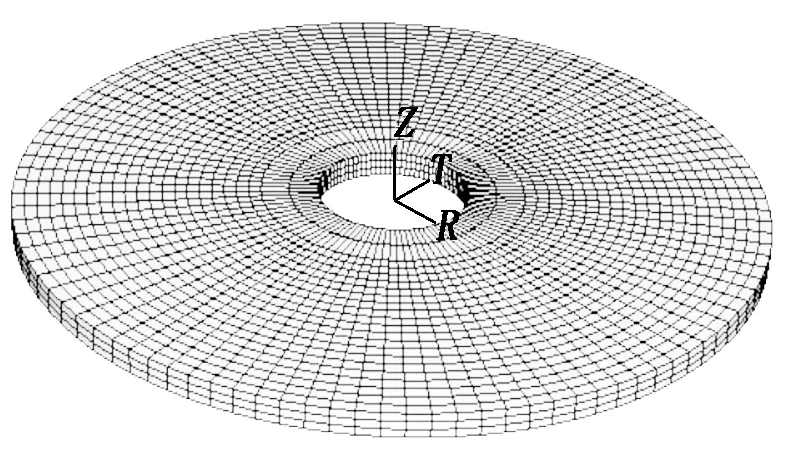
图3 坯料网格划分

图4 芯模网格划分
1.5 边界条件处理
1.5.1 接触边界条件处理
在ABAQUS中分别定义了坯料顶面接触面(Blank Top)、坯料底面外部接触面(Blank Bot Out)、坯料底面中心接触面(Blank Bot Core)、芯模顶面接触面(Mandrel Top Core)、芯模锥体接触面(Mandrel Body)、右旋轮接触面(Roller Right)、左旋轮接触面(Roller Left)以及接触对Roller Right-Blank Top、Roller Left-Blank Top、Blank Bot Out-Mandrel Body。由于模型中旋轮和芯模都视为刚体处理,故在以上的接触对定义中将右旋轮接触面、左旋轮接触面、芯模接触面都定义为主控表面,而坯料的所有接触面都定义为从属表面。
1.5.2 摩擦边界条件处理
锥形件强旋成形过程中需要采用简化的摩擦力学模型,旋轮与坯料之间的摩擦当成定摩擦来处理,而坯料与芯模之间的接触摩擦相对要简单得多,理想的状态是相对不发生摩擦,模型中视为无摩擦处理。因此,在锥形件强旋模型中定义了两种摩擦:Fric和Nofric。Fric定义坯料与旋轮之间的摩擦系数为0.04。Nofric指忽略表面间的摩擦,表征坯料与芯模之间没有摩擦。
2 模型可靠性验证
2.1 理论评估
在建模过程中,为了提高计算精度和效率,对不同单元类型、网格密度以及质量放大因子情况下的旋压过程进行了模拟分析。分析结果表明:当坯料采用六面体减缩积分实体单元C3D8R、网格划分情况如图3所示(单元数6 600个单元,节点数9 200个)、质量放大因子为225时,模拟所获得的伪应变能、动能与内能的比很小(如图5所示),说明本文所建立的模型是可靠的。
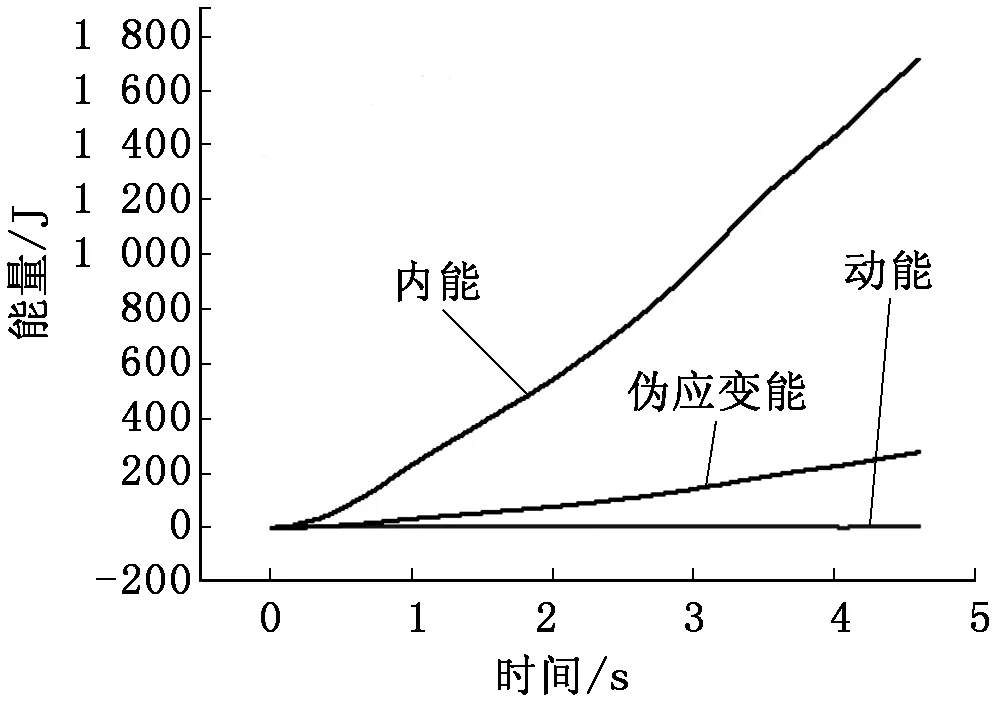
图5 锥形件强旋过程能量变化
2.2 实验对比
为了进一步验证本文所建仿真模型的可靠性,采用文献[5]实验参数为模拟条件,对材料为LF2M的坯料采用不同的偏离率进行了模拟计算,以壁厚差为评价指标,将计算结果与实验数据进行了对比,如图6所示。

图6 计算结果与实验数据对比
从图6中可以看出:计算结果与实验数据的壁厚差变化趋势基本一致,且最大误差不超过15%,表明本文所建立的三维有限元仿真模型是可行和可靠的。
3 结论
本文针对锥形件强旋变形特点,基于ABAQUS软件平台,在对几何模型、单元选择、材料属性设置、网格划分、边界条件等关键技术探讨与合理处理的基础上建立了三维有限元模型,理论评估和实验验证证明该模型与实际成形过程十分吻合。
