轴向气流中悬臂壁板颤振的理论及风洞实验研究

2020-11-05朱弈嶂杨翊仁

四川轻化工大学学报(自然科学版) 2020年5期

朱弈嶂，李鹏，梁森，杨翊仁

(西南交通大学力学与工程学院，成都 610031)

引言

轴向气流中的壁板结构在实际工程中有着非常广泛的应用，如大型机场、车站等建筑的顶棚均采用壁板(或壳体)设计。当柔性的悬臂薄板状物体放置在轴向流动的流体中时，壁板会受到持续的流体扰动。流体速度小于某一临界值时，扰动会趋于稳定而结构则处于稳定的静止状态；而速度超过某一临界值，扰动不会消失，这种现象被称为颤振失稳特性(flutter or flapping)[1]。Mechelin和 Doare论述了薄板颤振的现象在压电晶体能量采集中的运用[2]。

在早期关于颤振的研究中，Paidoussis[3]进行了轴向气流中柔软的阀门的理论与实验研究，发现因流速提高后的不稳定现象本质上是一种Kelvin-Helmholtz失稳现象。Zhang等[4]的实验研究使用了肥皂膜来维持二维特性，观察到了一种双稳定现象，即当给予一个足够大的扰动时系统将从稳定状态演化到不稳定的响应，有静止与振动两种稳定状态。Benjamin等[5]提出了一种流固耦合系统的仿真模型(FSDS)，文中采用3个无量纲的参数描述了二维板的颤振过程。李晋[6]研究了带有初始曲率的二维曲壁板的稳定性研究。Li和Zhang等[7-11]进行了一系列薄板颤振理论研究，如赫兹接触式位移约束置于轴向流中悬臂板，壁板颤振失稳、分叉现象及极限环响应，以及壁面效应对颤振的影响。实验方面，Watanabe等[12]观察到了气流中造纸工业半成品的颤振现象。Vandenberghe等[13]在风洞中进行了有关壁板稳定性的实验，发现了薄板颤振的双稳定现象。张德春等[14]对倒置的悬臂板进行了风洞实验，研究了壁板的静态失稳现象。

本文建立了轴向气流中薄板结构的颤振失稳理论的线性分析模型，采用行波解法获得了颤振临界状态下各无量纲参数之间的关系，并对特定试件的颤振临界速度进行初步预测，以指导后续实验。同时用迦辽金法，取悬臂梁的前两阶模态进行稳定性计算，结果与行波解的趋势一致。在理论工作的基础上，设计并制作了用于改善湍流度的整流罩，进行了风洞实验，测得包括铝板、铜板、ABS板在内的多个试件颤振速度与振动信号，最后对实验数据结果与理论预测结果进行对比分析。

1 壁板颤振的理论分析

本文考察的是轴向气流中放置悬臂式壁板，该壁板前缘受到固支约束而其后缘可自由运动，如图1所示。流场的均匀速度为U，密度为ρf；板的厚度为h，密度为ρs，长度与宽度分别为L和H。

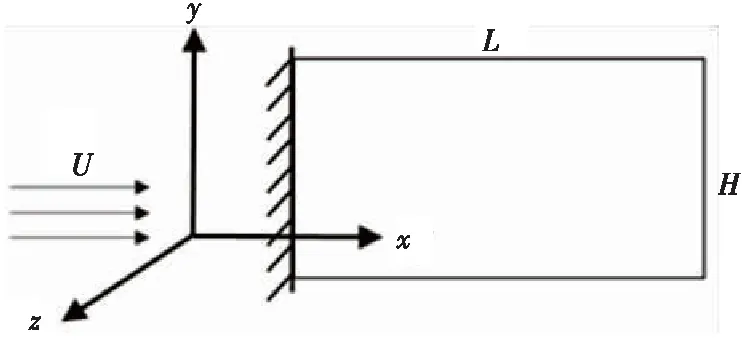
图1 悬臂壁板的力学模型

由于本文目的在于考察系统的颤振失稳特性，因此考虑壁板在小变形时的振动方程为[5]：

(1)

其中：EI为壁板的弯曲刚度，ma为流体力的附加系数，T为由流体粘性而导致的壁板表面上的张力，假设T遵从布拉佛斯层流边界层理论[5],则：

(2)

其中，Re为雷诺数。为便于理论分析，在下文中可取T的最大值，即

T(x)≈T(0)=1.3ρfV2LRe-1/2

(3)

对式(1)进行无量纲化，可得：

(4)

其中的无量纲参数定义为：

(5)

本文采用行波解法对系统可能发生颤振失稳进行分析以获得系统的颤振边界。假设w=Aekx-ωt[15]并与式(3)一起代入式(4)中可得：

(μ+cm)ω2+(cm-1.3Re-1/2)k2-

KBk4-2cmk=0

(6)

从上式可得：

对于本文考察的颤振失稳，应有Δ<0，即：

(7)

在势流条件下，根据Coene(1992)[15]提出的理论cm=ma/ρfL=2/k。因此在给定雷诺数Re与k后，可通过式(7)获得系统颤振边界(KB-μ)。图2描述了雷诺数Re=5×105时不同波数下系统的颤振边界。由图2可知，不同k值对应的颤振边界随质量比μ变化表现出类似的变化趋势，随着μ的增大，系统的颤振边界均会增大。图3给出了系统颤振边界随雷诺数Re的变化规律，由图3可知，当Re较小时(Re<5000)颤振边界对雷诺数变化较为敏感，但当Re较大时(Re>5000)其对颤振边界的影响较小。

图2 雷诺数Re=5×105时不同行波波长下的颤振边界

图3 行波波长k=2π时不同雷诺数下的颤振边界

上文对薄板颤振的预测是单模态的，下面对系统可能出现的多模态耦合颤振现象进行预测，采用的方法为伽辽金法。离散控制方程中的位移w，采用悬臂梁的前i阶模态，对控制方程进行时空分离：

w(x,t)=∑φi(x)·qi(t)

(8)

φi(x)=cosβix-coshβix+

ξi(sinβix-sinhβix)

(9-a)

(9-b)

其中，式(9-a)和式(9-b)为悬臂梁的第i阶模态表达式，可取前2阶模态进行计算。将式(8)中的每一阶模态代入控制方程中，乘以φj并自0至l作定积分：

(10)

为方便计算，无量纲参数合并为以下四个：

M=μ+cm,K1=cm-1.3Re-1/2，

K2=KB,C=2cm

(11)

取前两阶模态，即i,j=1,2, 并将积分后的方程写成矩阵形式，有：

(12)

式(12)为一个二次特征值问题。若解得特征值的实部为负，则系统的振幅变小、趋于稳定；若特征值的实部为正，则系统的振幅不断变大、系统发散，颤振失稳现象出现。

图4展示了各雷诺数下用迦辽金法计算得到的临界无量纲刚度与质量比的关系。曲线的上部表示稳定，而曲线的下方表示失稳的状态。图4中可观察到临界无量纲刚度随质量比的增加而增加，且在高雷诺数下粘性的影响对临界刚度的影响变化不明显，与图3展示的行波解结果一致。

图4 cm=1/π时的伽辽金解

2 壁板颤振的风洞实验研究

2.1实验模型设计

本实验采用的是Φ=1.2 m的开口式环流风洞。实验模型如图5所示。模型中，薄板沿着顺流向采用竖直方式放置以减小壁板自重而产生的静变形的影响。薄板前端预留60 mm的夹持段，并通过多根螺栓与夹持钢板连接。壁板模型安装完毕后，采用锤击法多次测试模型的固有频率并相应地调整模型安装，以保证实验模型在约束实现上与理论模型具有较高的吻合度。

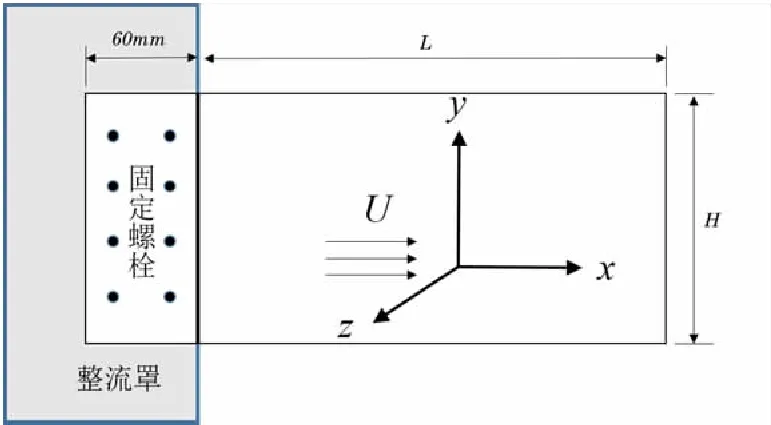
图5 实验模型示意图

由于螺栓凸起及外界数据线等会影响流场品质，因此设计整流罩来减小其对流场的影响。整流罩的设计采用NACA 64-008A AIRFOIL (n64008a-il)的翼型设计，其在低速条件下具有较好的降低阻力的效果。整流罩以木质骨架，上覆轻木板，再覆盖热缩膜制成。整流罩剖面如图6所示。事实上，如表1中的实验结果所示，整流罩是很有必要的，其对实验结果的影响达到了10%左右。

图6 整流罩剖面图

实验中采用中航电测BE120-3AA-P300应变片和DH5908H采集器作为测量装置。如图7所示，应变片粘贴于距离实验段前缘30 mm的中间高度处，实时测取该点振动信号，并判定颤振失稳状态及其对应的失稳临界速度。实验中分别采用风速缓慢升高和缓慢降低两种方式进行吹风实验，以保证实验结果的全面性。

图7 风洞实验安装示意图

实验中获取的薄板根部的动态应变可用作进一步分析。以铜板实验为例，测得的信号(经处理后)如图8所示，前部细长的响应为给予试件的激励。当风速未达到临界速度时，试件的振幅会迅速耗散；当达到临界速度时(如图中后部较宽的部分)，试件开始持续不断地颤振。此时稍稍减小风速，试件仍处于振动状态，且振幅稳定。继续减小风速，至恢复速度时，试件停止振动，振幅为0，停止记录。处理实验结果，截取颤振后较为稳定的一段数据并作傅里叶变换，即可得到临界速度时的颤振频率，如图9所示。

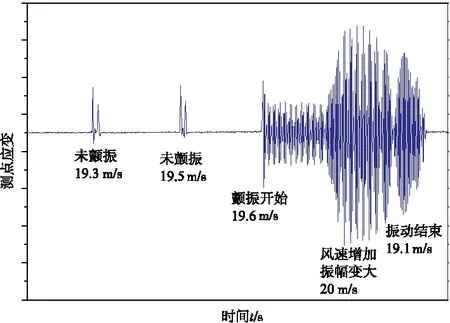
图8 典型的实验信号

图9 典型的实验测试结果

2.2实验结果及分析

为实现不同无量纲质量比，本文选择了铜板、铝板、ABS板等3种材料的薄板进行了实验，模型的颤振临界速度的实验结果见表1。实验发现，模型在风速升高及降低两个测试过程中将出现不同的颤振临界速度，分别记作：Uin和Ude(表1)。这种有趣的现象可称为颤振失稳的迟滞效应。

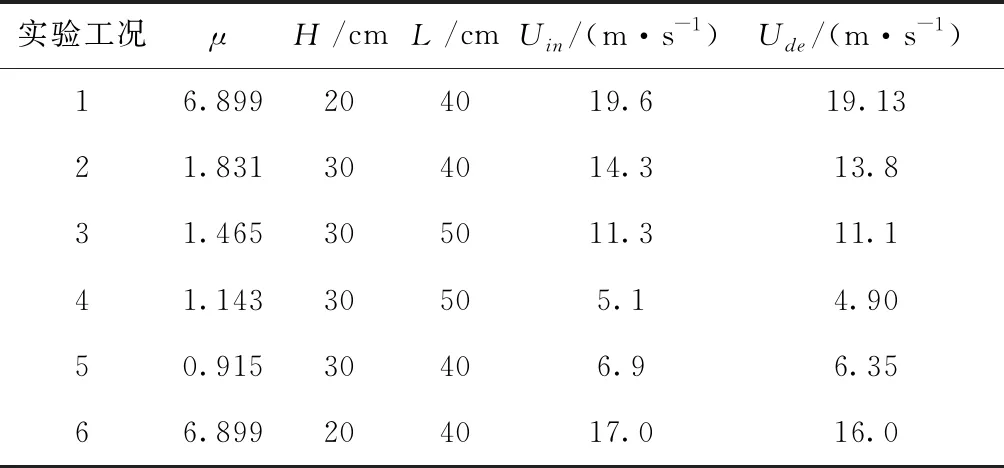
表1实验结果

对表1中每一组试件进行吹风实验，可测得颤振时的参数KB的值，称其为颤振边界值，结果如图10中试验值所示。考虑选取等截面悬臂梁横向振动频率方程的第二、三个特征根及其中间的取值来估算系统的颤振边界，即k=4.694(≈1.5π),6.28(≈2π),7.854(≈2.5π)，结果如图10中本文理论结果所示。从这些结果可知，正如理论预测，实验中壁板会出现颤振失稳现象。实验中测得的壁板处于颤振失稳时典型的振动信号及其功率谱图分别见图9，从图9可知，壁板处于单频的周期振动，并符合颤振的运动特征，壁板出现了单模态颤振失稳。实验结果表明，颤振速度随着质量比的增大呈阶梯增长趋势。图10中还展示了文献[16]及文献[17]的结果，二者分别基于数值涡格方法和有限入流非定常气动力理论，计算了悬臂壁板的颤振失稳时的无量纲参数，颤振边界也出现了剧烈的增大趋势，这也与本文的理论和实验结果相吻合。事实上，这种现象与颤振模态的转变密切相关：当系统质量比较小时，系统的失稳模态接近于高阶模态失稳；而当系统具有较大的质量比时，系统的失稳模态却是以二阶模态为主。这说明，随着系统质量比的增大，系统的颤振失稳模态会发生跳跃和转变。