带有负刚度装置的超音速壁板稳定性分析

杨石芪， 李 鹏， 杨翊仁

(西南交通大学力学与工程学院， 成都 610031)

引 言

负刚度是指力的增量与位移的增量比值为负的现象，例如在压杆稳定系统中，当轴向力大于欧拉临界力时结构失稳，此时横向力与位移曲线的斜率就是负的；在弹塑性力学中，结构出现塑性变形，结构力位移曲线出现下降段，此时结构刚度为零或者为负。

传统的被动线性隔振器，使用小刚度从而获得小的固有频率，但是会出现大的静态位移。为了克服这个问题，需要设计一种非线性隔振器，具有大的静态刚度和小的动态刚度。有很多方法可以获得这种非线性特性。Le[1]以两对称的NSM装置并联正刚度结构组成隔振系统用于汽车座椅，用来改善系统在低频激励下的隔振效果。研究表明，NSM系统对低频激励有显著的隔振效果；含NSM装置的系统的质量位移响应均方根(RMS)从原来激励的268.5%降低至67.2%。Carrel[2]利用两根斜弹簧组成NSM与垂直弹簧并联组成非线性隔振系统，通过调整参数可以使得系统在静平衡位置的动刚度为零，并使得系统可以在拥有小静态变形的同时具有小刚度的特性。David[3]提出用两根预压杆组成的NSM，可以使得原子力显微镜(AFMs)的噪音水平下降2～3倍；可以使AFMs得到更加清晰的图像；也可以使得AFMs在更加恶劣的环境中工作。Huang[4]研究了由欧拉杆作为NSM的非线性隔振器。理论研究显示，系统可以根据激励的赋值大小表现为纯软化、混合软-硬化、纯硬化刚度系统；实验结果表明在考虑加速度传递率时，系统有更宽的隔振频率范围。在附加阻尼的影响下，系统在高频段的衰减性能有所下降。Dong[5]研究了由磁负刚度弹簧(MNSS)并联螺旋弯曲弹簧组成的隔振器。理论和实验结果表明，MNSS可以降低隔振器的共振频率；把隔振频率扩宽至低频范围。Han[6]对用弧形弹簧滚柱装置并联竖直弹簧的非线性隔振器进行了研究。理论研究显示提高阻尼比可以降低响应峰值；实验表明非线性隔振系统与线性隔振系统相比有优良的低频隔振性能；对于某一确定隔振器，限制激励赋值和适当增加阻尼器可以获得更好的隔振效果，适当过载可以获得更低的隔振频率。

虽然NSM在系统隔振中表现出较好的性能优点，但其在超音速壁板流致振动的控制中的应用还未见相关报道。本文以带有NSM在超音速流作用下的二维壁板为研究对象，以研究NSM对壁板临界失稳特性的影响规律。文中考虑几何非线性，采用一阶活塞气动力模型，应用Galerkin离散方法把偏微分方程化为常微分方程，利用Hopf分岔代数判据[7]给出系统的临界流速和颤振频率，调整NSM位置考察其对系统的影响。

1 NSM装置

本文采用一种较为简单的负刚度结构形式[2,8-9]，如图1所示。两水平弹簧刚度为Kh，竖直弹簧刚度为Kv，水平弹簧原长L，水平弹簧在平衡位置的压缩量为s，两连接杆长度为a。水平弹簧的一端与支座连接在一起，另一端与滑块连接，滑块可以在水平方向上自由滑动，滑块的另一端与连接杆铰接在一起。当连接杆处于水平位置时，竖直弹簧处于原长状态，两水平弹簧的弹簧刚度相同，所以结构在此状态下是稳定的。

图1 能实现负刚度的装置示意图

当结构产生x位移时，有：

(1)

引入无量纲参数：

(2)

将式(1)对位移求导，并考虑式(2)，则无量纲刚度与无量纲位移之间的关系为：

(3)

图2～图4展示了不同参数对系统无量纲力-位移曲线和刚度-位移曲线的影响。

图2 不同r1的无量纲力-位移和刚度-位移曲线(r2=1,r=1)

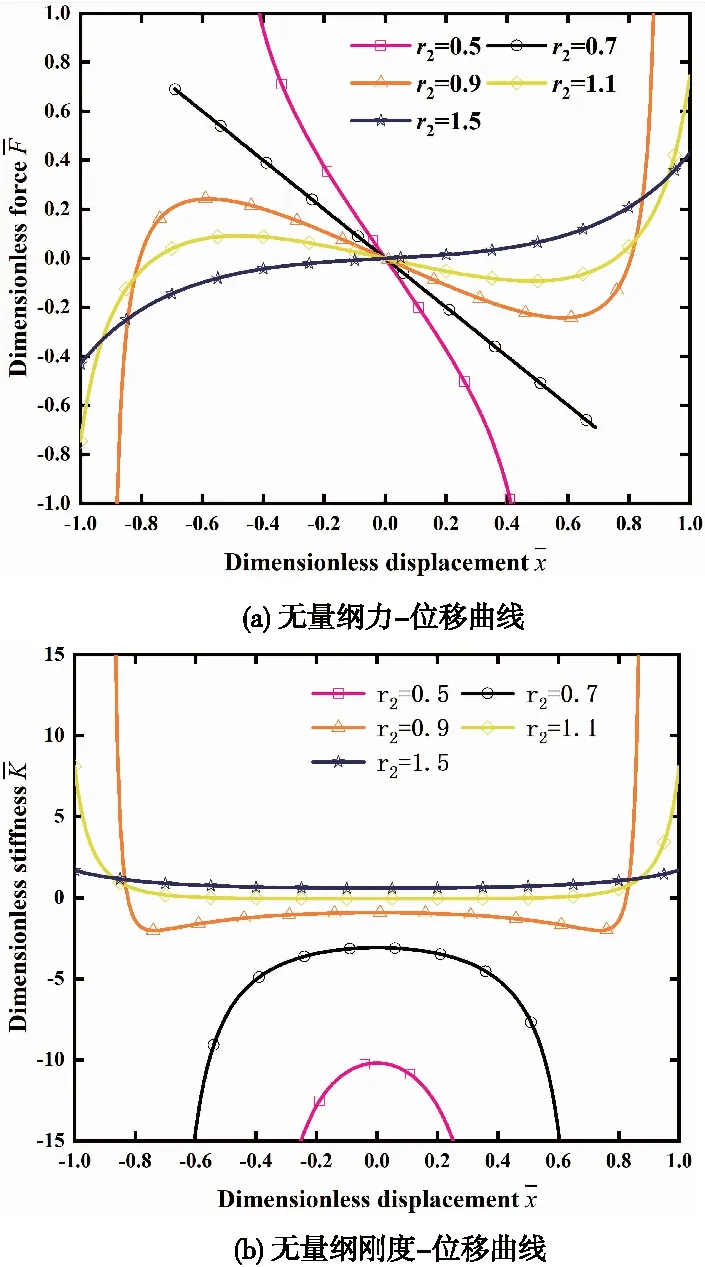
图3 不同r2的无量纲力-位移和刚度-位移曲线(r1=0.7,r=1)

图4 不同r的无量纲力-位移和刚度-位移曲线(r1=0.7,r2=1)

由图2可知，当r1<0.4时，系统并不能作为NSM使用；即使当r1>0.4时，系统可作为NSM，但也只是在一定范围内起作用。这一结论也在图3中得到了验证，由图3可知，当r2比较小时，系统可以一直当NSM使用，但此时位移变化的范围却较小。图4表明刚度比r对系统有显著影响。当r比较小时，水平弹簧不足以抵消竖直弹簧的能力，此时系统刚度保持为正值而不能作为NSM使用。

2 带NSM的超音速二维壁板控制方程

考虑如图5所示的对边简支带有NSM的二维壁板在超音速流作用下的力学模型，板长为a，板厚h，板密度为ρ，弹性模量为E，横向位移为w(x,t)。上表面有沿x方向超音速气流，其速度为U∞，马赫数为M∞，空气密度为ρ∞。

图5 带有NSM的二维壁板在超音速气流作用下的力学模型

根据Hamilton原理，采用修正的一阶线性活塞气动力模型[10],得到系统控制方程为：

(4)

取无量纲参数：

(5)

将式(5)代入式(4)，得到：

(6)

选择满足对边简支边界条件的模态函数，并采用Galerkin方法对式(6)进行离散，可得：

(7)

3 系统的稳定性分析

根据文献[11]，对式(7)取前两阶模态进行理论分析，展开得到：

(8)

其中：G=q1sin(πr)+q2sin(2πr)

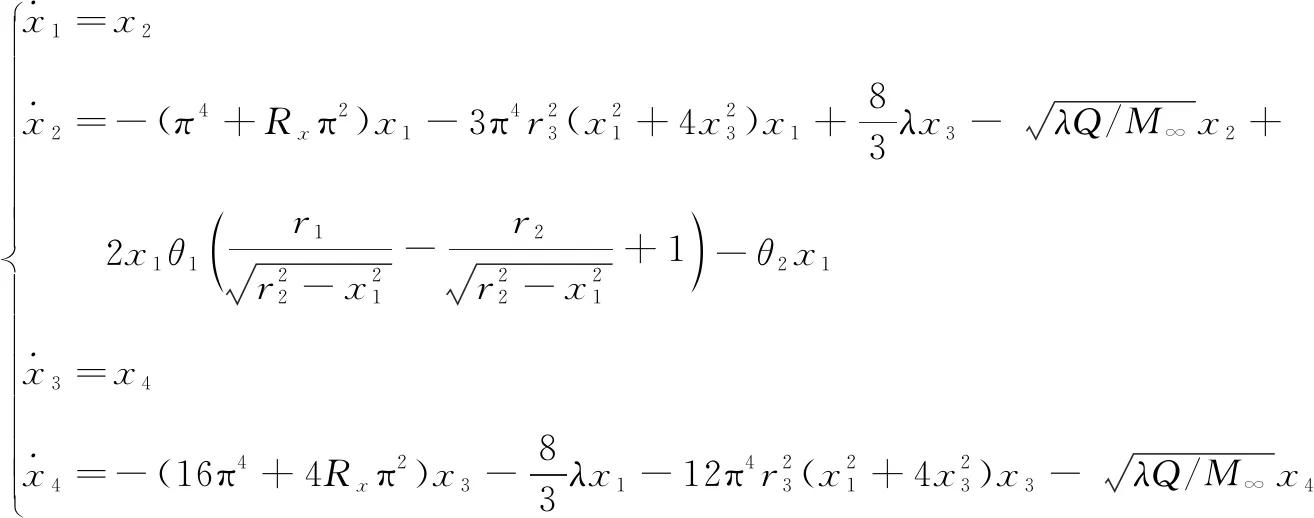
(9)

显然(x1,x2,x3,x4)=(0,0,0,0)为式(9)的平衡点，此平衡点处的Jacobian矩阵对应的特征方程为：

s4+p1s3+p2s2+p3s+p4=0

(10)

其中：

(11)

根据文献[7]的定理1，系统存在一对纯虚根，且其他根具有负实部，需Δ3=0,Δ1>0，其中Δi为式(10)的第i阶Hurwit行列式。由Δ3=0得到临界流速为：

(12)

其中：

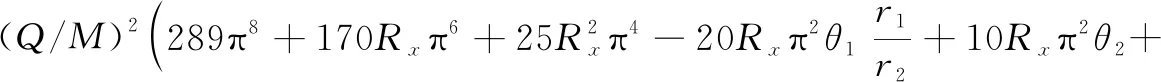
由文献[7]中的定理2，得到系统的颤振频率为：

(13)

4 算例分析及讨论

参照文献[12-14]，选取下面的一组参数：

E=70 GPa,h=2.5 mm，a=800 mm，ρ=2700 kg/m3，μ=0.3其他无量纲参数取：

Rx=-2.5π，M∞=2，Q=0.02，θ1=20，θ2=15，r1=0.7，r2=0.8。根据前面的讨论，可以得到临界流速和颤振频率，见表1。

表1有/无NSM的壁板颤振临界流速和颤振频率比较

由表1的结果可知，NSM可以起到提高壁板的颤振临界流速的效果。图6给出了NSM在板不同位置时系统颤振临界流速和颤振频率的变化曲线。由图6可知，系统的颤振临界流速对NSM的位置较为敏感，其随着NSM位置的变化呈现单峰值的非线性关系；NSM位于板的中部位置时，系统的颤振临界流速有较大的提高；而在靠近两端时，系统颤振临界流速却会有明显的降低；系统的颤振频率随着NSM位置变化也呈现相似的规律，但其始终要低于没有使用NSM的系统。

图6 NSM在不同位置对结构的影响

5 结束语

本文研究了带有NSM的二维壁板在超音速流作用下的稳定性，建立了带有NSM的大变形二维壁板控制方程，利用Hopf分岔代数判据得到颤振临界流速和颤振频率。结果表明：NSM可以提高壁板的颤振临界流速；NSM在板中间部位时会提高系统的临界流速，NSM靠近板的两端时会降低系统的临界流速；NSM始终会降低系统的颤振频率。

需要指出的是，采用本文的NSM虽然可以提高系统颤振临界流速，但其提高幅度还有待进一步加深，这可能需要采用更为复杂的NSM而实现，这也是下一步需要开展的工作。