不匹配扰动下逆变器系统的固定时间扰动观测器设计
2020-11-05王创创陈昌忠
高 升, 王创创, 唐 含, 陈昌忠
(四川轻化工大学自动化与信息工程学院, 四川 自贡 643000)
引 言
随着国际上环境保护意识的不断增强和新能源技术的巨大进步,充分利用可再生能源和大力推动能源转换相关技术领域进步已成为世界各国的共识[1]。智能电网和可再生能源系统的发展,电压源逆变器已成为电力转换过程中关键要素之一[2]。
DC-AC逆变器系统在不间断电源[3]、可再生能源系统[4]、交流电机驱动[5]等得到了广泛的应用,在功率转换中起着重要的作用。在这些工业领域中,对于逆变器的控制精度和响应速度要求也越来越高。
PID控制和无差拍控制方案因其实现的简单性曾广泛地应用于逆变器控制。但是由于负载的剧烈变化会导致控制效果大打折扣,这些形式简单的控制方案对于工业水准要求越来越高的高新产业已经无法满足需求[6]。实际上,扰动广泛存在于控制系统并且会影响系统的控制效果,从而导致系统不稳定,甚至对设备产生损坏[7]。因此,对于扰动的消除问题吸引了极大地关注。其中扰动估计技术在消除扰动影响问题上发挥了巨大的作用[8]。目前涌现出许多利用扰动估计技术的优秀逆变器系统控制方案,例如扰动观测器(Disturbance Observer)[9-11],扩展状态观测器(ESO)[12-13],基于谐波扰动观测器的控制(HDOBC)[2,14],还有通过将扰动观测器与反步法结合起来的基于扰动观测器的反步法控制(DOPBS)[8]等。然而以上这些控制方案还存在一些问题,它们的观测器都是渐近稳定的,这就意味着产生的扰动无法在一个有限时间内被准确地预测出来,并且理论上扰动观测所需的时间越长,系统稳定所需的时间也就越长[7]。为了解决这一问题,研究人员设计了利用高阶滑模微分器的有限时间观测器[15-16],有限时间稳定系统比渐近稳定系统的收敛速度更快,并具有更好的鲁棒性。但是由于滑模控制中不连续的切换控制会产生抖振问题。因而产生了基于添加功率积分器的反馈控制[17],与前述控制方法不同的是,此反馈方法并非简单地消除系统的非线性部分,而是利用了系统的非线性项,从而降低了控制的输入[18]。
有限时间的扰动观测和有限时间的控制方案虽然相对于渐近稳定有了很大的进步,但是仍存在一些缺点。比如,有限时间稳定的收敛时间与初始条件有关,这样就可能会在初始条件增加的情况下使得系统收敛时间持续延长[7]。但在某些需要明确知道收敛时间的场合,需要更加严格的固定时间控制。固定时间控制的前提便是要有一个固定时间的观测器,以达到在一个固定的与初始条件无关的时间内对扰动进行准确地估计。基于对以上问题的分析研究,本文针对具有不匹配的扰动的DC-AC逆变系统,对扰动进行了固定时间估计,并通过模拟实验对实验结果进行了验证。
1 典型DC-AC逆变器系统模型
本文选择基础的、也是在实际中广泛应用到的单相全桥电压源DC-AC逆变器系统来进行分析并建立模型,如图1所示,其他逆变器均可由其经过修改,拓展得到。

图1 典型的单相全桥DC-AC逆变器系统电路图
图1中,Vdc是直流端的电压;逆变器主电路由四个转换开关S1-4组成;L是LC滤波器的电感;C是LC滤波器的电容;Z代表负载包括线性电阻和非线性部分。在此模型中,逆变器开关输出的电压Vin是PWM波,根据状态空间平均法可得:
Vin=uVdc
(1)
其中:u∈[-1,1],是由控制器得到的占空比函数。根据电路图使用基尔霍夫电压和电流定律可以得到:
(2)
其中:iL是电感的电流,Z是负载,vo是电容C的输出电压。
结合式(1)和式(2)得到逆变器系统的动力学方程:
(3)
然后以vr表示参考电压。令x1=vr-v0。便可得到以下形式:
(4)

(5)
对x2进行求导,并结合式(4),可以得到:
(6)

需要特别注意的是,在式(6)中负载产生的扰动d(t)作用在输出通道上,而输入控制u却作用在输入通道上,因此在本系统中负载产生的扰动d(t)被称作不匹配扰动[2,19]。

最终得到逆变器系统扩展的状态方程如下:
(7)
2 定义及引理
2.1固定时间稳定和一致有限时间稳定
给定微分系统:
(8)
其中:x∈Rn,f:Rn|→Rn是一个非线性函数。假设原点是系统(8)的平衡点。
定义1[20-21]系统(8)的原点是有限时间稳定的平衡点,如果满足原点是李雅普诺夫稳定的并且存在一个函数T:Rn|→R+,称作稳定时间函数,对于任意x0∈Rn,系统(8)的解x(t,x0)满足limt|→T(x0)x(t,x0)=0
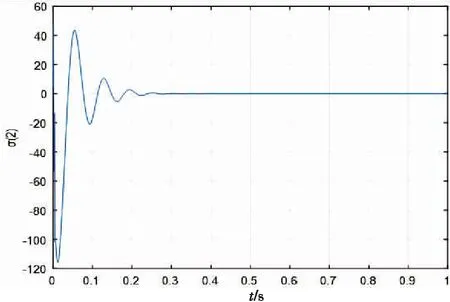
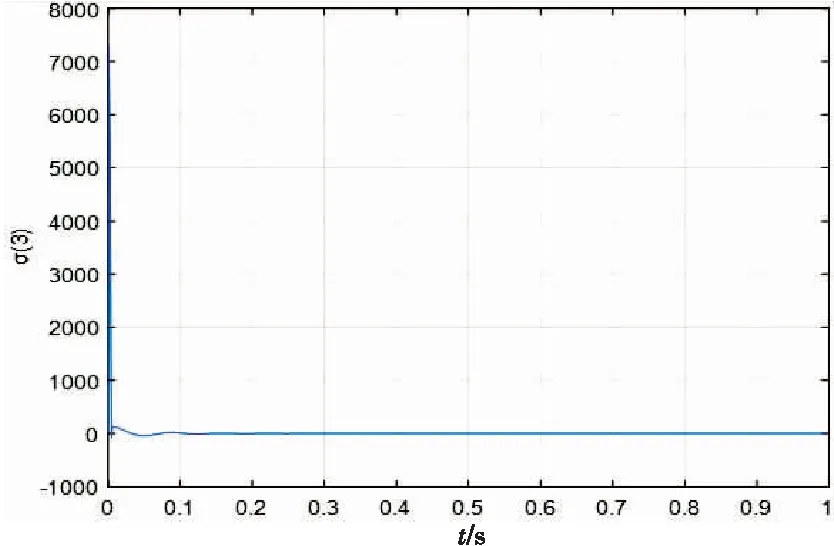
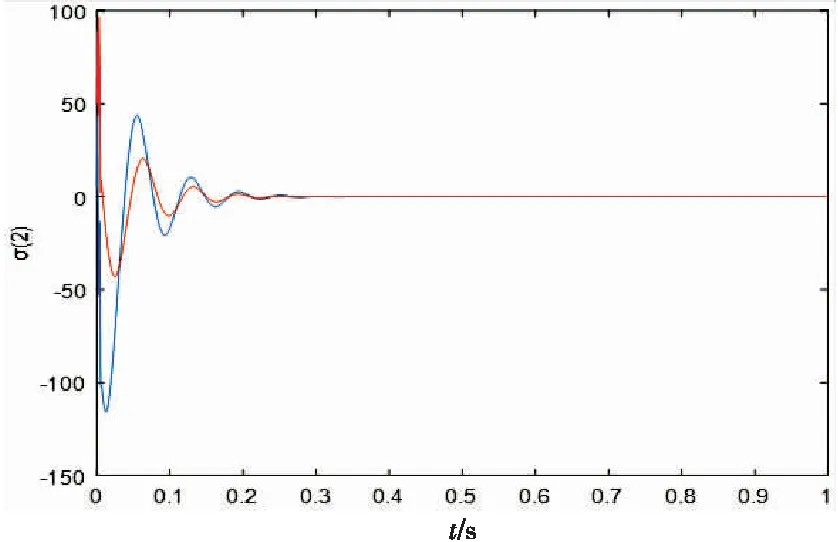
定义2[22-23]系统(8)的原点称作是固定时间稳定平衡点,如果它在一个有界的时间T(x0)内满足全局有限时间稳定,并且对于稳定时间函数T:Rn|→R+来说,存在一个有界的正定常数Tmax,使得T(x0) 说明固定时间稳定与有限时间相比最大的优点便是可以得到一个与初始条件无关的收敛时间上限,而这个上限只与系统的参数有关,这样便意味着基于固定时间设计的误差观测器会有更快的误差估计和更灵活的调整时间。同时也就更便于设计合适的抗干扰方案。 定义3[24]考虑如下系统: (9) 其中: 有限时间收敛意味着在有限时间内可以达到准确的收敛。满足一致收敛特性意味着对于任意初始值,收敛时间对于一个常数一致有界。 定义4[25]把r=(r1,...,r2)看作广义上的权重向量,其中ri>0。关于权重向量的扩张可以记作Δr:(x1,x2,...,xn)|→(λr1x1,λr2x2,...,λrnxn),其中λ>0。 (2) 当且仅当一个函数f满足等式.λ-mf(Δrx)=f(x)时,称这个函数f在x∈Rn和λ>0上满足关于权重r的齐次度为m的齐次性。 齐次性可以用来证明得到有限时间稳定性和一致收敛性。下面给出引理1和引理2做补充说明。 引理1[20,24]如果f:Rn→Rn是一个齐次度为k<0的局部吸引的齐次向量场,可以得到f是有限时间稳定的。 引理3[26]对于乘积空间X×Y,其中Y是紧集。如果一个开集N包括X×Y中的片集{x0}×Y,那么N也就包含着关于{x0}×Y的管集W×Y,其中W是x0在X上的一个邻域。 引理4[27]如果连续实值函数V1与V2相对于l1>0和l2>0的v是齐次的,并且V1是正定的,那么对于所有的x∈Rn满足以下不等式: 对于系统(7)中的误差,固定时间的干扰观测器可以实现,可以在一个与初始估计误差无关的常数为上界的有限时间T内实现准确的估计。 固定时间的扰动观测器设计如下: (10) (1) 指数αi和βi的选择方式为αi=(i+1)α-i,βi=(i+1)β-i。其中:α∈(1-ε1,1),β∈(1,1+ε2),ε1,ε2是足够小的正实数。 (2) 指数ki(i=1,2,3,4)的选取需要满足如下矩阵为Hurwitz矩阵: (3) 函数θ: [0,∞ )→{0,1}通过如下方式选择: 其中:Tu是稳定时间,通常通过反复试验进行选择。 综上设计,便可以得到如下定理。 定理利用观测器(10),可以在以恒定的T1为上限的有限时间t1内,准确地估计扰动系统状态及扰动,即x1,x2,x3,x4,而与初始估计误差无关。 (11) 当t≤Tu,θ=0,系统(11)为: (12) 在所选李雅普诺夫函数V的前提下,S={σi∈R4:V(1,σi)=1}是一个紧集。因为M={(β,σi)}是一个包含片集合{1}×S的开集,根据引理3,M也包括有围绕片集合{1}×S的管集合(1-ε1,1+ε2)×S。 (13) (14) 当t=Tu,李雅普诺夫函数V(β,σi)满足: (15) 当t>Tu,系统(11)可表示为: (16) (17) 因为α<1,可以得到以V(Tu)为初始值的李雅普诺夫函数将会在有限时间里收敛到零。因此,误差系统(11)将会在有上界的有限时间内收敛到零,这个上界可以表示为: (18) 由上述证明可知,系统的状态和干扰都会在经过以不随初始值变化的T1为上界的有限时间t1内得到准确的估计值。 根据本文固定时间观测器的设计条件以及多次试验调整,选择系统的仿真参数为:k1=3.8×103,k2=4.8×105,k3=3.9×107,k4=3.9×107,α1=0.98,β1=1.02,Tu=0.02,ω=100。估计误差σ1、σ2、σ3、σ4随时间变化的仿真结果分别如图2~图5所示。 图2 估计误差σ1随时间变化的曲线 图3 估计误差σ2随时间变化的曲线 图4 估计误差σ3随时间变化的曲线 图5 估计误差σ4随时间变化的曲线 从图2~图5所示的仿真结果可以看出,观测器所产生的各个观测误差均在极短的时间内收敛,并且在0.3 s之前均已经取得了逆变器系统的准确观测值。 此外,为了说明本文研究的先进性,在参数选取上与前文保持一致的情况下,将观测结果与此前针对逆变器系统的较为先进的有限时间谐波观测器[2]的观测结果进行对比仿真。为了便于直观呈现,选取4个数据中收敛时间最长的估计误差σ2来对比说明。 (1) 在相同条件下对比两种观测器的效果,结果如图6所示。 图6 两种观测器下估计误差σ2随时间变化的曲线 从图6可以看出,在相同条件下,固定时间观测器比谐波观测器有着更快的收敛速度和相对更小的绝对值。 (2) 分别对比两种观测器的在初始误差不同的情况下对收敛时间的影响。在上文基础上对两组观测器的初始误差取值适当增大的情况下继续做出对比仿真,结果分别如图7和图8所示。 图7 谐波观测器在不同初始估计误差下σ2随时间变化的曲线 图8 固定时间观测器在不同初始估计误差下σ2随时间变化的曲线 由图7可知,在初始误差增大的情况下,谐波观测器的σ2图像有了明显的变化,绝对值增大,并且收敛时间也显著增加了。而从图8可以看到,在初始误差增加相同程度的情况下,固定时间观测器收敛时间等各项指标基本未发生变化,收敛时间保持不变。以上结果验证了固定时间扰动观测器的观测时间与初始条件无关,相比谐波观测器来说,具有明显的优越性。 本文研究了不匹配扰动下的逆变器系统的扰动观测问题。首先对逆变器系统进行谐波化建模,然后利用齐次性原理,设计了一种新的固定时间观测器。该观测器可以在一个与初始条件无关的固定时间对系统的状态和扰动进行准确地观测。仿真结果证明了所提出的观测器的有效性和准确性。在以后的工作中要把本文的结果与控制方法进行结合,实现逆变器系统的固定时间稳定控制。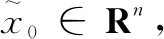

2.2齐次性定理


3 固定时间的谐波干扰观测器设计



4 仿真与分析




5 结束语
