结合双阈值定位与透射率约束的航拍图像去雾
2020-11-05王伟鹏项文杰戴声奎
王伟鹏, 项文杰*, 戴声奎
(1. 闽南科技学院 光电信息学院,福建 泉州 362332; 2.华侨大学 信息科学与工程学院,福建 厦门 361021)
1 引 言
随着航空技术和飞行器技术的快速发展,航拍图像成为获取地形地貌信息的高效方式。然而雾霾天气带来的不良影响使得航拍图像的质量严重退化,具体表现为颜色饱和度降低、细节可见性不足,导致其在地面测量、目标定位和灾情预报等系统中难以发挥有效作用。因此对图像进行去雾处理具有重要的应用价值和实际意义[1-2]。图像去雾研究是一项富有挑战性的工作,由于单张图像中的雾气浓度是未知的,并且很难捕捉到同一光照下的完全无雾场景作为参考,因此该问题的解决一直受到制约。
目前,主流的去雾方法大致可分为两类。一类是基于先验假设的模型复原方法,此类方法以物理模型为基础,充分利用场景的特征提出假设、约束条件,反推模型实现清晰图像的估计。He[3]等人提出了暗通道先验规律,结合大气散射模型进行图像去雾,方法简单且效果出众。Meng[4]等人提出针对传输透射率的边界约束条件,结合正则化方法进行建模,有效消除了图像噪声,提高了对比度。Sun[5]等人对大气亮度进行细化,提出基于局部大气亮度估计的去雾算法,有效改善了局部细节恢复的视觉效果。Wang[6]等人提出基于线性变换的透射率估计方法,并采用弱化策略克服局部区域的失真问题,达到自然清晰的恢复结果。Bui[7]等人构造彩色椭球体用于透射率的估计,能够有效提升去雾图像的对比度,且避免颜色过饱和现象。Sebastian等人提出两种估计透射率的方法,一是采用多层感知器对最小通道图直接进行计算[8],二是结合暗通道先验和形态学快速重建[9]。Liu[10]等人采用自适应正则化方法,有效保持透射率的深度结构。宋瑞霞[11]等人对包含大片天空的图像进行分割,结合色调映射实现图像去雾。杨燕[12]等人利用高斯函数对原始场景和去雾场景进行衰减拟合,修正透射率实现区域补偿。
另一类是基于神经网络的学习方法,此类方法通过大量数据的训练实现图像去雾,然而受限于样本的数据量和多样性,对部分自然有雾图像的处理效果欠佳。Cai[13]等人将大气散射模型与卷积网络相结合,提出深度学习的端到端训练系统,以此准确估计传输透射率。Ren[14]等人提出一种利用多尺度深层神经网络的学习方法,用于原始图像和透射率之间的映射,对自然场景与合成图像均取得较好的去雾结果。陈清江[15]等人对雾化场景和清晰结果之间的残差构造学习网络,结合多尺度卷积实现雾气分布特征的提取,再利用导向滤波恢复图像。邢晓敏[16]等人通过二阶映射策略进行样本训练,提出非配对数据的适应性对抗网络。
考虑到航拍地形地貌具有细节丰富多样且基本不含天空的特点,采用当前主流方法估计大气光强度和透射率会出现一定的偏差。针对该问题,本文提出一种结合双阈值定位大气光与约束优化透射率的航拍图像去雾算法,并采用基于人眼特性的色调映射提升视觉效果。实验表明,该方法的处理效果和算法执行效率具有较大的优越性。
2 大气散射模型和暗通道先验
在计算机视觉和图形图像学中,雾霾天气下的图像降质过程可用大气散射模型[3-4]来描述:
I(x)=J(x)t(x)+A[1-t(x)]
(1)
式中:I(x)和J(x)分别表示有雾图像和去雾后的清晰图像;A表示全局大气光强度值;t(x)表示介质透射率,当大气均匀分布时,t(x)=e-βd(x),β为大气散射系数,d(x)为景物深度。观察式(1)可知,只有I(x)是已知的,若要求解J(x),需要先求出大气光A和透射率t(x)。
He[3]等人通过对大量户外无雾图像进行观察统计,总结了暗通道先验规律:除了天空和其他大面积白色区域以外的图像局部块中,至少存在一个RGB通道值趋近于零的像素。对于彩色图像J(x),其暗通道图像可表示为:
(2)
式中:Jc表示图像J的一个颜色通道;Ω(x)表示以像素点x为中心的局部方形区域。假定大气光强度已知的前提下,计算式(1)等号两边的暗通道:
(3)
由于I(x)是有雾图像,其暗通道值不为零;而J(x)是清晰的无雾图像,其暗通道值非常低,趋近于零,因此舍弃等号右边第1项,得到介质透射率[3]的表达式:
(4)
式中:引入调整因子κ(0<κ≤1)用于控制去雾程度,为了保证图像的视觉效果一般取κ=0.95。通过暗原色先验估计得到的透射率存在块效应现象,还需要以原始图像的结构边缘为参照,经过软抠图或者导向滤波进一步细化。然而软抠图的时空复杂度较大,引导滤波的参数不易调整都将导致复原效果不理想。
3 本文算法
基于大气散射模型,本文重点对大气光和透射率的估计、恢复图像的色调调整进行深入研究。本文的算法流程如图1所示,实现步骤如下:1)分别提取雾天图像的梯度图和暗通道图,采用双阈值分割大气光值所在区域;2)依次通过条件约束和双指数滤波优化透射率;3)恢复图像并进行色调映射调整。

图1 本文算法的流程图Fig.1 Flow chart of the proposed algorithm
3.1 双阈值定位大气光强度
大气光强度位于原始图像中雾气浓度最大的区域,其估计值对复原图像的亮度产生影响:取值偏大将导致图像的亮度偏暗,取值偏小则会造成高亮像素值溢出。暗通道方法[3]选取最高亮度值的前0.1%,标记这些像素的所在位置,将雾天图像中对应位置上的像素最大值认定为大气光A。Ren[14]等人选取透射率中最暗的前0.1%像素,对应雾天图像中的最大强度值作为A。上述方法仅单方面考虑了图像亮度来决定A值的估计,针对基本不含天空且场景细节丰富的航拍图像,鲁棒性不足。考虑到地面上的白色建筑、目标物较多,并且雾气分布较为均匀,本文提出一种融合边缘检测与暗通道的估计方法,通过双阈值来确定大气光强度的估计。
首先,浓雾区域的梯度信息相对较弱、边缘细节不明显,因此利用Sobel算子对原始图像进行边缘检测,获取梯度图g(x),梯度值越小说明该区域越平滑,为了限定大气光所在的浓雾位置,应设定梯度阈值Tg为较小的数,此处取Tg≤gm·10%(gm表示g(x)的整体平均值)。其次,由暗通道先验可知,雾天图像的暗通道值Idark(x)随着雾气浓度的升高而增大,浓雾区域的亮度一定是Idark(x)中相对较高的,此处取亮度阈值Td≥Im·90%(Im表示Idark(x)中的最大灰度值)。最后,分别标记满足g(x)
估计过程如图2所示,图2(a)为边缘梯度图,暗区表示细节不明显的平滑区域;图2(b)为暗通道图,其亮度近似反映雾气浓度。接下来进一步对阈值的选取问题进行研究,通过3组不同阈值的定位结果,讨论对大气光强度的估计影响:第1组取Tg=gm·10%,Td=Im·90%,自动定位结果如图2(c)中的红色标识,此时阈值门槛较低,导致标识的浓雾区域较大,绝大部分位于图像最上方,深度最深处,然而小部分标识出现错误,如接近白色的建筑并非浓雾所在位置;第2组设定高门槛阈值,取Tg=gm·1%,Td=Im·99%,结果如图2(d)所示,不难发现仅有最上方的少数红色标识满足阈值条件,对于含有噪声的雾天降质图像,少量像素的均值计算不具有鲁棒性,因为这些像素本身可能是噪声点;第3组折中取Tg=gm·5%,Td=Im·95%,结果如图2(e)所示,可以看出红色标识区域的大小介于前两者之间,既可有效避免图2(c)中非浓雾的白色目标干扰,又具有比图2(d)更强的噪声鲁棒性。

图2 大气光强度的估计Fig.2 Estimation of the atmospheric light
综上分析可知,阈值的设定直接影响大气光强度的定位和计算准确度,因此在本文实验中,选取Tg=gm·5%,Td=Im·95%可得到合理、准确的结果。
3.2 构造约束条件估计透射率
介质透射率的准确估计是恢复清晰图像的关键。针对航空航拍图像中,地面具有丰富的细节特征,考虑到透射率与场景深度相关,深度一致时,透射率基本相同,因此假设局部区域的相邻像素具有相似的透射率[4]。然而针对深度跳跃的区间,该假设并不成立,因为透射率也会随之跳跃。此处引入加权函数W(x,y)进行约束:
W(x,y)[t(x)-t(y)]≈0
(5)
式中:x和y表示相邻的2个像素点。权重W(x,y)对x和y进行条件约束:当x和y的深度差值非常大时,W(x,y)应取很小值才能使式(5)成立。由于单幅图像的深度信息是未知的,无法直接构造加权函数。考虑到深度跳跃的图像边缘,若局部区域的像素点具有相似的颜色或亮度,则其深度值基本一致,此处采用相邻像素的颜色差和亮度差来构造加权函数:
W(x,y)=e-‖I(x)-I(y)‖2/2σ2
(6)
W(x,y)=(|l(x)-l(y)|α+ε)-1
(7)
式中:‖I(x)-I(y)‖表示颜色向量的差值;|l(x)-l(y)|表示对数亮度通道的差值;σ是规则参数;α是控制亮度差的灵敏度系数;ε是很小的常数,防止被除数为零。在全局图像中引入加权约束条件,实现透射率的正则化[4]:
(8)
式中:Ω表示图像域;ωx表示以x为中心的局部图像块。引入差分算子,将式(8)离散化:
(9)
式中:I为图像像素的索引集;wij为W(x,y)的离散形式。调整式(9)中的求和顺序,引入微分算子,得到:
(10)
式中:⊗为卷积运算,Dj为一阶微分算子,Wj为加权矩阵。通过最小化以下目标函数求解透射率:
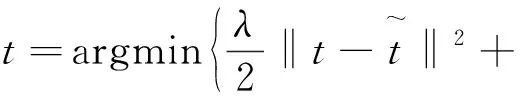
(11)
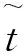
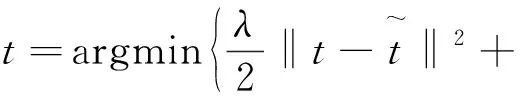
(12)
该估计结果还不能完全反映深度信息,如图3(a)所示,局部区域的纹理细节所在深度基本一致,需要进一步滤除。

图3 本文算法对透射率的估计Fig.3 Estimation of transmittance by proposed algorithm
3.3 双指数滤波优化透射率
双指数滤波器[17]具有快速平滑去噪的特点,且有效克服了双边滤波器的梯度反转现象。该滤波器将透射率t(x)分解为一维信号,先执行正向递归滤波:
φ(x)=[1-τ(x)λ]t(x)+τ(x)λφ(x-1)
(13)
τ(x)=r[t(x),φ(x-1)]
(14)
再执行反向递归滤波:
φ(x)=[1-ρ(x)λ]t(x)+ρ(x)λφ(x+1),
(15)
ρ(x)=r[t(x),φ(x+1)]
(16)
式中:指数滤波核r(i,j)=exp[-(i-j)2/(2σ2)];λ和σ用于控制细节的平滑程度。联合正反向滤波输出,即可得到优化后的透射率:
(17)
如图3(b)所示,优化后的结果中已滤除纹理细节,仅保留灰度差较大的轮廓特征,与原始图像的深度信息基本相符。
3.4 恢复图像和色调映射
由透射率和大气光强度即可反解大气散射模型[3-4]恢复清晰的结果,即:
(18)
式中:引入下限参数t0=0.03,目的是为了防止透射率接近0时受到噪声干扰。图4(a)为雾天航拍图像,恢复结果如图4(b)所示,通过对比可以看出,雾气被有效去除的同时,对比度和视见度有所提升,但是去雾之后光线不足,整体色调偏暗。为了使恢复效果得到进一步提升,研究基于人眼视觉特性的色调映射方法。韦伯心理学和物理学定律[18]指出,人眼对于视觉信号强度的波动感知和反应是由背景亮度刺激加权的。在散射模型中,图像的背景可用透射率来简单表示。本文将这一定律融入恢复图像的色调调整,结合透射率的平均亮度进行非线性拟合,得到映射公式如下:
(19)
式中:tm为透射率tb(x)的平均值;JW(x)为映射后的结果,如图4(c)所示,相比映射前,色彩更加鲜艳饱满,层次感和细节可见性得到进一步提升。

图4 本文的去雾效果Fig.4 Defogging results by proposed algorithm in this paper
4 实验结果与对比
为了验证本文算法的有效性和优势,与He算法[3]、Cai算法[13]、Ren算法[14]和Sebastian算法[8]进行对比,客观指标采用信息熵E和平均梯度G。实验平台为MATLAB 8.5.0,运行环境为Win10系统,机器配置为Intel i5 CPU,2.2 GHz主频,4 GB内存。
4.1 主观比较
本文的实验测试选用了包含城市、江河、山林、湖泊和海岛等多种地形地貌特征的航拍图像,多种算法的去雾效果如图5所示。图5(a)为有雾图像,图5(b)为He算法[3]的去雾结果,img1和img5的整体亮度偏低;img2的树木细节不明显;img3和img6的建筑物颜色过于饱和;img4和img7的远景处出现偏紫色和偏蓝色现象。图5(c)为Cai算法[13]的去雾结果,img1和img2的对比度较差;img3和img6的整体去雾力度不足;img4、img5和img7的远景处仍然残留部分雾气没有消除彻底。图5(d)为Ren算法[14]的去雾结果,img1和img3的亮度适宜,但是色调与原始图像有一定偏差;img2和img4取得较好的恢复效果,然而视觉上的层次感不足;img6的雾气去除程度有待提高;img7整体偏绿色。图5(e)为Sebastian算法[8]的去雾结果,img1、img2和img3亮度偏暗,对比度较差;img4、img5和img7的远景处还有小部分雾气存在;img6的色彩饱和度不足,颜色信息丢失。图5(f)为本文算法的去雾结果,img1、img2和img3整体明亮通透,色调与原始图像高度一致;img4、img5和img7远景处视见度较高,细节清晰可见;img6去雾彻底,色彩保真度较好。通过以上7组图片的对比可知,本文算法在主观视觉上的优势较大。

图5 实验结果比较Fig.5 Comparison of experimental results
4.2 客观比较
图5中7组图片的客观指标如表1和表2所示。信息熵E表征图像中信息量的大小,数值越大意味着信息量越多;平均梯度G反映细节的清晰程度,数值越大表明图像越清晰。从单张图片的对比可以看出,本文的E指标和G指标具有一定的优势。进一步统计2项指标的平均值,本文均取得最高值,再次验证了本文算法的有效性。对比各种算法的运行时间,结果如表3所示,本文构造约束条件估计透射率的复杂度相对较低,算法运行效率相对较高,处理1 024×768分辨率的图像仅需1.39 s,比其余算法节省至少60%的时间。
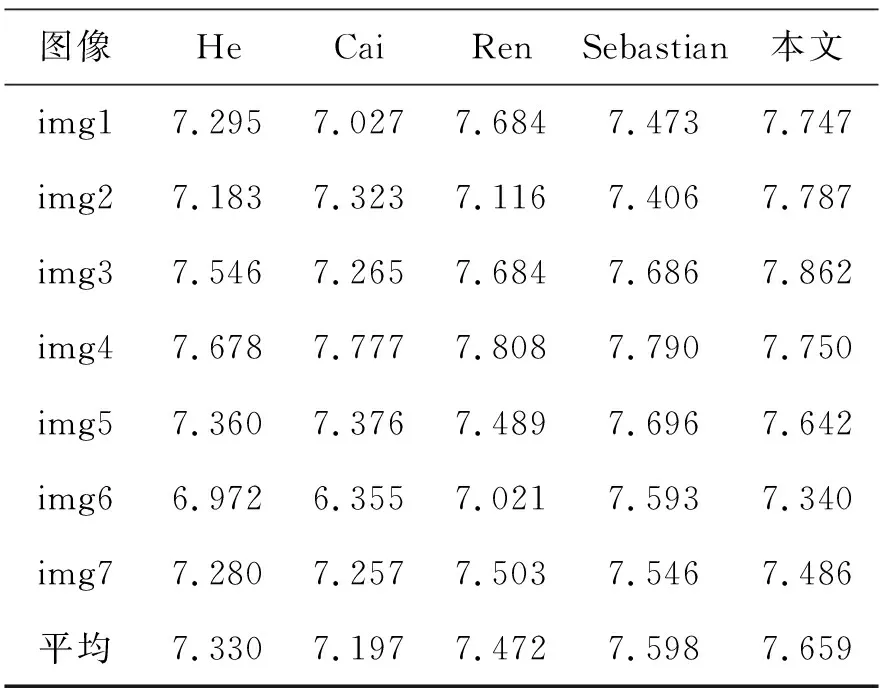
表1 信息熵E的对比Tab.1 Comparison of information entropy
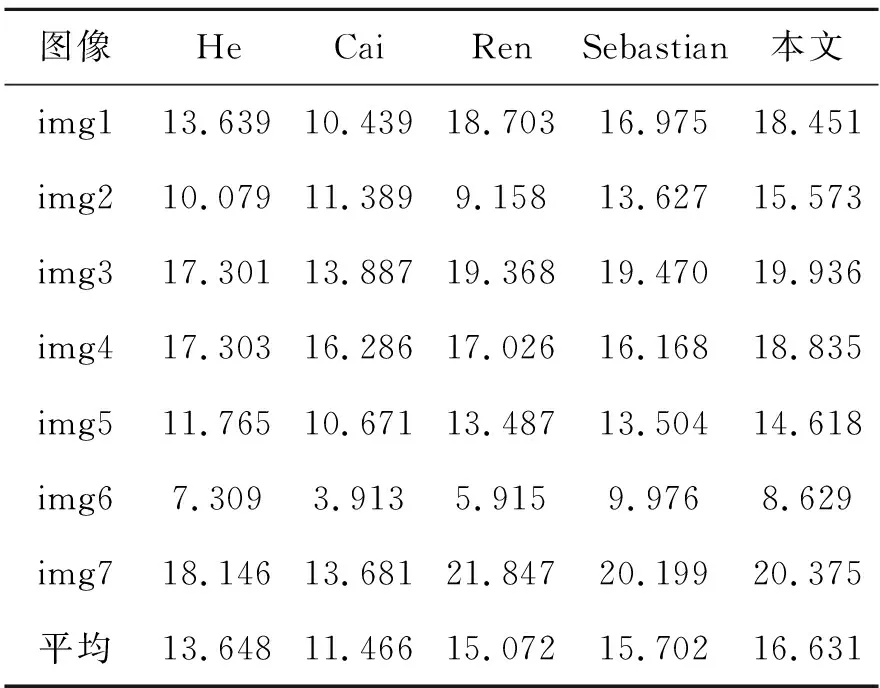
表2 平均梯度G的对比Tab.2 Comparison of mean gradient

表3 运行时间的对比(s)Tab.3 Comparison of Running time(s)
5 结 论
针对航拍设备在雾天采集图像引起的细节模糊和颜色退化问题,本文给出了快速有效的恢复方法。根据梯度图的细节分布特征和暗通道的亮度信息,采用双阈值定位大气光强度所在位置;构造约束条件与双指数滤波的有效结合,进一步优化了细节处的透射率值;提出基于人眼特性的色调映射方法,改善恢复图像的视觉效果。实验结果表明,本文方法所获取的透射率与深度信息具有高度一致性,7组测试图像的平均信息熵为7.659,平均梯度为16.631,均优于现有算法。同时算法的时间复杂度低,能够有效应用于遥感定位、地貌测绘、目标识别等航拍系统。
