基于泊松分布的非局部均值图像去噪方法

高晓玲

(宁夏大学 新华学院，宁夏 银川 750021)

1 引 言

在图像获取与传输时，光照变化及传感器本身的因素会使输出的图像受到噪声的污染。在基于光子计数的成像系统中，如合成孔径雷达成像、天文学成像及医学成像等，获取的图像中均含有泊松噪声[1]。泊松噪声是一类乘性噪声，在图像灰度值越大的位置其噪声能量也越大。图像中的泊松噪声不仅影响了图像的视觉效果，同时给特征提取、分类等后续图像处理操作带来了较大的精度影响。因此，在图像的预处理过程中亟需去除图像中的泊松噪声。

经典的图像泊松去噪思想是将图像中的泊松噪声通过方差变换为高斯噪声，然后利用双边滤波[2]、小波去噪[3]、非局部均值[4]等高斯去噪方法进行处理。当成像光子数较多时，经典的图像泊松去噪方法能取得较好的去噪效果，然而，在天文学和医学成像系统中，在成像时接受的光子数通常较少，使得输出的图像灰度较低，经典方法难以去除图像中的泊松噪声[5]。

当前，图像的泊松去噪方法较多。文献[6]提出了基于极大似然估计的泊松去噪方法，该方法能取得很好的去噪性能，但其计算复杂度较高。随后，文献[7]提出了一种基于Haar变换的快速图像泊松去噪算法，并通过与软阈值方法进行对比，验证了该方法的有效性。Federica等人[8]将全变分函数正则化模型应用于图像的泊松去噪，并根据实验验证了该方法在去噪的同时保持图像细节信息的能力，但该方法去噪容易引起阶梯效应。为此，文献[9]结合对偶算法对全变分正则化进行了改进，增强了算法的去噪性能和边缘细节保留的能力。Xu等人[10]针对正则化函数，结合函数的一阶和二阶导数，提出了能消除阶梯效应的正则化泊松去噪方法。Marnissi等人[11]结合泊松分布的对数似然函数和正则化方法，提出了贝叶斯极大后验泊松去噪方法，并通过求解偏微分方程来实现泊松去噪过程。Sun等人[12]在贝叶斯极大后验框架下，建立了泊松噪声的稀疏正则化模型，利用迭代的方法求解冗余字典的系数稀疏。

另一类应用广泛的方法是对非局部均值方法的改进。Houdard等人[13]基于非局部均值的思想，并结合泊松分布的特性，得到了非局部均值泊松去噪方法，该方法能自适应迭代求解出最佳的去噪参数。文献[14]针对光子数较少的条件下，提出了一种基于主成分分析的非局部均值泊松去噪方法，该方法结合字典学习和泊松分布的统计特性，利用Bregman距离求解字典的稀疏，实验证明该方法在强泊松噪声的条件下能很好地保留图像的细节信息。文献[15]提出了基于泊松分布的随机距离去噪方法，采用像素间的随机距离大小来衡量图像中两像素点间的相似性大小，该方法在不同光子数条件下验证了其去噪的有效性。

基于图像泊松分布的统计特性，本文提出一种基于泊松分布的非局部均值图像去噪方法。该方法利用像素点的非局部区域内的像素信息并根据极大似然估计其泊松分布参数；根据两泊松分布间的L2范数距离来表示两像素点间的差异大小。采用两像素点周围邻域内点对间的L2范数距离平方和来定义相似性权值的大小。依据非局部均值的思想对图像进行泊松去噪，实验证明，本文方法在不同光子数条件下均能取得较好的去噪性能，特别是在光子较少时，该方法能很好地保留图像的细节信息，获得较高的峰值信噪比(Peak Signal-to-Noise Rate, PSNR)[16]。

2 非局部均值算法原理

非局部均值算法是在图像中寻找出与待滤波像素点相似的像素点，构成一个非局部区域，根据非局部区域内像素点进行加权平均滤波得到去噪后的像素值。对于图像中的一像素点x，在其周围邻域Ω(x)内计算各像素点与x之间的相似性，以确定像素点x的非局部区域NL(x)。依据非局部区域NL(x)内各像素点的相似性权值进行加权平滑滤波。

在非局部均值滤波中，两像素点之间的相似性权值是根据像素点周围邻域内点对之间的距离平方和来定义的。对于图像中的像素点x与y，其间的相似性权值w(x,y)定义为[4]：

w(x,y)=e(-d2(x,y)/h2)

(1)

式中：h为滤波控制参数，d2(x,y)为像素点x与y邻域之间的距离平方和，其定义为：

(2)

式中，η表示用来计算两像素点之间相似性的窗口大小，I(x+t)表示像素点(x+t)处的像素点灰度值，Ga(t)表示方差为a的高斯核。

在计算了像素间的相似性权值之后，滤波后的像素值u(x)可由式(3)计算：

(3)

在加权平滑滤波过程中，窗口中心像素点处的相似性权值由于d(x,x)=0的影响使得x处的相似性权值最大，且远大于其他像素点的相似性权值，这样将导致去噪结果受自身像素点的影响较大，影响去噪性能。为此，在实际滤波过程中，窗口中心像素点的相似性权值取为滤波窗口Ω(x)中的最大相似性权值，即，

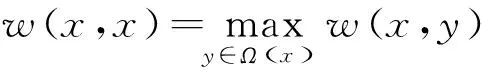
(4)

非局部均值滤波的性能受滤波控制参数h的影响较大，当h的取值较大时，滤波窗口内各像素点的相似性权值差别较小，滤波效果越接近均值滤波；当h的取值较小时，滤波窗口内各像素点的相似性权值差别较大，其去噪能力较弱；当h取值非常小时，滤波效果由少数几个点来决定，去噪性能大大降低。因此，合理选择h的参数对去噪性能至关重要。

3 基于L2范数的非局部均值泊松去噪

3.1 像素点泊松分布的参数估计

在天文学、合成孔径雷达、医学成像等系统中，传感器在固定时间内接受一定数量的光子数而形成输出图像。图像中含有大量的泊松噪声，泊松噪声具有一定的随机性，依据泊松噪声的统计特性，对图像中的每一个像素点建立泊松分布模型，

(5)

式中，r表示传感器接受的光子数，λ是真实光子率。文献[17]表明，当光子率λ>20时，此泊松分布近似于高斯特性，可用高斯分布来建模。

式(5)中泊松分布的参数为真实光子率λ，在图像中，取待滤波像素点x周围最相似的k个点组成一个非局部区域NL(x)，依据极大似然准则估计参数λ。对于图像中的两像素点x与y，其间的相似性dxy由对应邻域窗口η(x)与η(y)内的像素点灰度差的平方和来计算，即

(6)

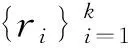
(7)

对式(7)求导可得，

(8)

由式(8)可得参数λ的非局部极大似然估计，

(9)

3.2 像素点间的相似性权值求解

对图像中的每个像素点x利用其非局部区域内的点估计出一个泊松分布p(r;λx)后，所有像素点的泊松分布组成一个待滤波图像。在待滤波图像中的两点p(r;λx)与p(r;λy)，利用L2范数计算其间的相似性，

(10)

将式(5)代入式(10)可得，

(11)

化简上式，

(12)

实验中采用蒙特卡洛方法来计算其数值近似值。在进行非局部均值滤波过程中，取待滤波图像中一点λx处的非局部区域NL(λx)中的k个数值点。对于待滤波图像中的两点λx与λy，其间的相似性权值可由式(13)计算给出，

(13)

式中，λx,l表示λx的非局部区域内的第l个点，ρ表示滤波控制参数，d(λx,l,λy,l)为两点λx,l与λy,l之间的L2范数。

基于两泊松分布间L2范数的计算和待滤波图像中两点间相似性权值的计算，对于一幅含泊松噪声的图像，其去噪算法的步骤为：

步骤1：对图像中的每一个像素点根据式(6)选取最相似的k个点组成非局部区域NL(x)；

步骤2：根据图像中每一个像素点的非局部区域NL(x)内的像素点，利用极大似然估计出泊松分布的参数λ；

步骤3：所有的泊松分布构成一个待滤波图像，依据式(13)计算待滤波图像中两点间的相似性权值；

步骤4：利用非局部均值思想进行去噪。

根据上述基于L2范数的非局部均值图像泊松去噪方法的思想，其去噪的基本流程如图1所示。

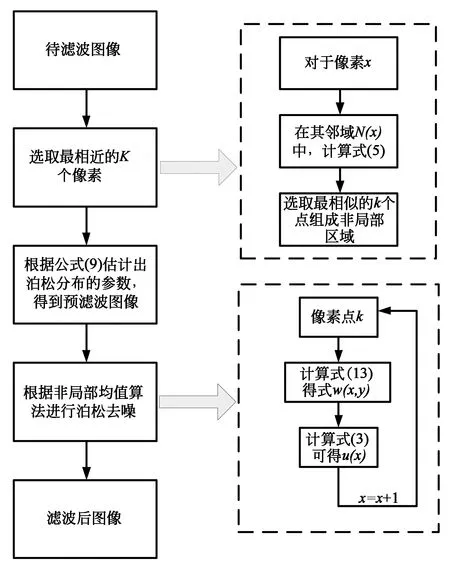
图1 本文图像去噪方法的基本流程Fig.1 Basic procedure of the proposed image denoising method

4 实验与分析

为了验证本文算法的去噪性能，利用4幅图像仿真加入泊松噪声进行去噪实验，本文算法(简称L2 NLM)的去噪性能与非局部均值算法(NLM)[4]、泊松非局部均值算法(Poisson NLM)[18]以及泊松主成分分析算法(Poisson PCA)[17]进行比较。在实验中，每个像素的邻域窗口取20×20，非局部区域由k=25个点组成，滤波窗口的大小取为7×7，NLM算法中的滤波控制参数h=0.7，Poisson NLM算法中的滤波控制参数h=1.5，本文算法的滤波控制参数h=1.1。

采用峰值信噪比来衡量去噪性能，在图像“Barbara”和“Peppers”中分别加入PSNR为10 dB和20 dB的泊松噪声，利用上述4种算法进行去噪，所得的结果如图2～5所示。

从图2～5的结果可以看出，NLM的去噪性能较差，图像较模糊，Poisson NLM和Poisson PCA的去噪性能较好，细节保持能力较好。相比于L2 NLM，其他3种算法在去噪性能和边缘细节信息保持方面均较差。从视觉效果上可以看出，L2 NLM去噪后的图像更清晰，结构更明显。

图2 PSNR为10时，不同算法对“Barbara”的去噪结果。Fig.2 Illustration of “Barbara” denoising results of different algorithms when PSNR is 10 dB

图3 PSNR为20时，不同算法对“Barbara”的去噪结果。Fig.3 Illustration of “Barbara” denoising results of different algorithms when PSNR is 20 dB

图4 PSNR为10时，不同算法对“Peppers”的去噪结果。Fig.4 Illustration of “Peppers” denoising results of different algorithms when PSNR is 10 dB

图5 PSNR为20时，不同算法对“Peppers”的去噪结果Fig.5 Illustration of “Peppers” denoising results of different algorithms when PSNR is 20 dB

为了定量比较本文算法的去噪性能，在4幅图像中分别加入PSNR为1、5、10 dB的泊松噪声，分别利用上述4种算法进行去噪，计算去噪后图像的PSNR，对比结果如表1所示。从表1的结果可以看出，L2 NLM在4幅图像中的去噪性能均好于NLM，且优于Poisson PCA和Poisson NLM的去噪性能。在PSNR取值较低时，L2 NLM的性能大幅优于其余算法的性能，而在PSNR取值为5 dB和10 dB时，L2 NLM的去噪性能同样是最优。上述实验结果充分验证了本文算法的性能优势。

5 结 论

本文提出一种基于泊松分布的非局部均值图像去噪方法，采用像素点非局部区域内的信息估计出一个泊松分布，利用L2范数计算两泊松分布间的距离，从而定义两像素点的相似性大小，图像中两点之间的相似性权值大小由各自邻域内点对间泊松分布的L2范数距离的平方和来定义。在不同峰值信噪比下进行去噪实验，本文方法的去噪图像峰值信噪比均优于22 dB。通过分析比较不同算法的去噪性能，验证了本文去噪的性能优势。