基于地球同步轨道InSAR每日生成DEM质量分析

杨泽发，张庆君，丁晓利，陈武

a School of Geosciences and Info-Physics, Central South University, Changsha 410083, China

b Department of Land Surveying and Geo-Informatics, The Hong Kong Polytechnic University, Hong Kong 999077, China

c China Aerospace Science and Technology Corporation, Beijing 100048, China

1. 引言

数字高程模型（DEM）被广泛应用于土木工程、水文监测、重力场模型构建、城市规划管理以及应急响应等实际应用中。为支持其在不同领域中的应用，需要快速生成并及时更新DEM产品。目前，DEM的生成方法众多，包括传统的大地测量技术[如全站仪以及全球导航卫星系统（GNSS）]、机载激光扫描技术（Li-DAR）、摄影测量技术以及合成孔径雷达干涉测量技术（InSAR）。其中，摄影测量和InSAR属于遥感技术，其相比于传统的大地测量方法，可以以较低的成本获取高空间分辨率的DEM产品。鉴于InSAR技术具有全天候、全天时的优点，该技术也成为了当前生成大范围区域DEM产品的首选遥感技术[1-3]。

尽管InSAR技术在生成DEM方面具有独特优势，但现有的机载或近地轨道（LEO）星载合成孔径雷达（SAR）传感器却难以频繁（如每天）生成或更新大范围区域（如大陆或全球）的DEM产品。其主要原因主要有两个方面：首先，使用机载或航天飞机SAR传感器生成大范围区域的高分辨率DEM产品价格昂贵且相当耗时。例如，为获得近乎全球（覆盖了约80%的地球陆地）的高分辨率（约30 m）DEM产品，由美国航空航天局、地理空间情报局以及德国和意大利航天机构实施的航天飞机雷达地形测绘任务（SRTM）共花费2.2亿美元，耗时11天（即1999年9月16—27日）[2,4]。其次，由于卫星重返周期有限（通常为数十天）且空间覆盖范围较小，因此难以利用低轨星载雷达干涉测量技术实现DEM产品的每日更新。例如，德国航空航天中心利用2010—2014年大约四年的TanDEM-X SAR干涉对[5,6]制作了全球DEM产品。

地球同步合成孔径雷达（GEOSAR）概念最初由Tomiyasu [7,8]提出，用于以更高的频率对地进行观测，其飞行高度约为36 000 km，可以以相当短的重返周期（如24 h，甚至只有几十分钟）获取大范围（如在Scan-SAR模式下覆盖范围约为8×107km2）、高空间分辨率（如几米）的SAR影像[9,10]。一般而言，利用GEOSAR技术可获得亚厘米级精度[10]的三维（3D）位移分量，并通过由多个GEOSAR卫星组成的星座提供24 h的全球灾害监测，这一主题在近期引起了广泛讨论[11-14]。此外，利用GEOSAR数据估算大气相位的潜力也已被讨论[15-17]。

GEOSAR的巨大潜力在于它能够对大范围区域（如全球）的DEM产品（如全球）实现每日更新，其每日（或更短）的重返周期可以为全球DEM的生成（或更新）提供每日的合成孔径雷达干涉测量。此外，较短的重返周期可以有效限制GEOSAR干涉测量时的时间失相干现象[18]。因此，利用GEOSAR甚至可以生成植被茂密地区的DEM。此外，与LEO SAR系统（通常为几公里）相比，GEOSAR系统通常可以提供更大的临界基线（比如数百公里）[19]，这意味着大多数GEOSAR数据可用于DEM的生成。

本文将系统地分析GEOSAR系统应用于全球每日DEM产品生成或更新中的潜力，特别是生成的DEM产品质量。为此，本文首先概述基于InSAR技术的DEM生成方法，然后分析GEOSAR InSAR的主要误差来源和局限性及其对所生成的DEM产品质量的影响。

2. 基于InSAR生成DEM

地球表面的高程信息可以通过InSAR干涉相位来估算[19]。图1描绘了重轨干涉测量系统的观测几何，其中，A1和A2分别代表空间基线为B的SAR天线两个位置；α是空间基线相对于水平方向的倾角；H和θ分别为SAR天线A1的高度和入射角；ρ和ρ + Δρ分别是SAR天线A1和A2到地面同一目标之间的距离；Z(y)表示目标点高程。从图1可以得出[20]：

令φ为天线A1和A2的解缠相位差，Δρ为天线A1和A2与地面同一目标之间的斜距差，则有：

结合式（1）至式（3），可以得到干涉相位φ与地面高程Z(y)之间的关系公式：

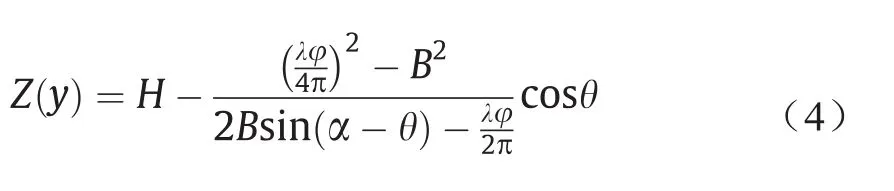
3. GEOSAR生成DEM的误差分析

如公式（4）所示，高程值Z(y)与卫星高度H、斜距ρ、视角θ、波长λ、空间基线B、倾角α和干涉相位φ相关。其中的某些参数（如波长λ）可以精确确定并视为无误差，而其他参数，如斜距、空间基线、倾角、卫星高度差和干涉相位都有可能含有误差。在本节中，我们将基于参考文献[10]中使用的系统参数来分析这些误差对GEOSAR DEM生成的影响（表1）。

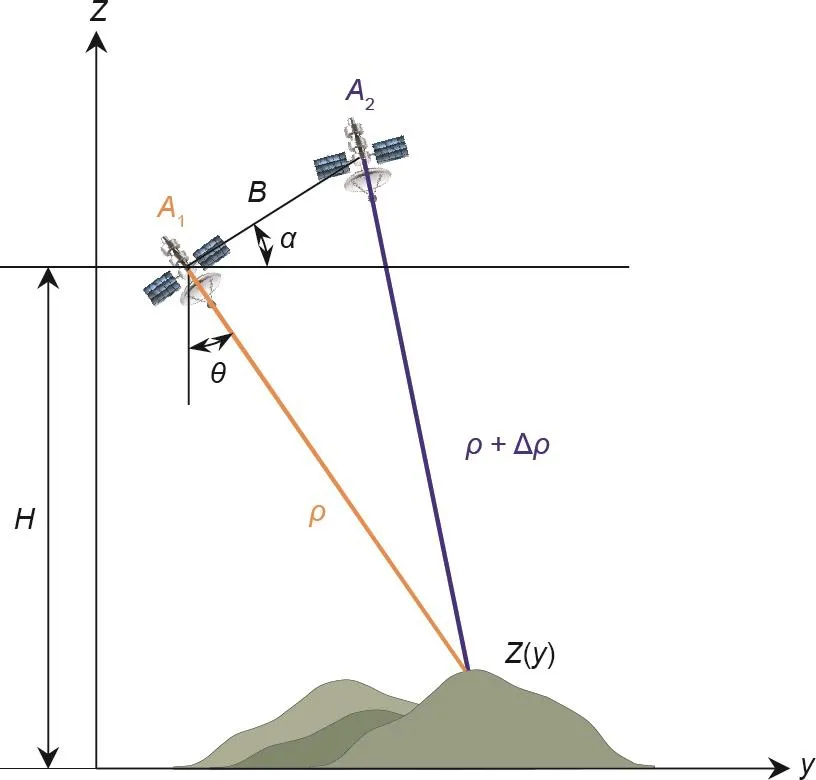
图1. 用于生成DEM的InSAR二维观测几何。

表1 分析中采用的GEOSAR系统的参数[10]

3.1. 斜距误差

假设误差源彼此独立，则根据公式（1）可计算得到斜距误差δρ对基于InSAR技术估计所得的DEM的影响：

图2为由式（5）计算得到的斜距误差导致的GEOSAR DEM的不确定度。为便于分析，本文使用名义入射角（即4.8°）进行计算。结果表明，斜距误差与DEM估计误差呈线性形式。考虑到斜距误差（主要是由于对流层和电离层的延迟导致）可能高达数十米甚至数百米，因此其对DEM估计的影响十分显著，应尽可能减小。这个问题将在4.3节中再次详细讨论。

3.2. 空间基线误差

根据式（3），空间基线误差δB对GEOSAR DEM生成的影响可表示为：

由式（6）可知，空间基线误差对GEOSAR DEM生成的影响主要取决于斜距ρ、视角θ、基线倾角α和空间基线B。其中斜距和视角可由成像几何精确确定。因此，基线误差的传播主要取决于空间基线长度和基线倾角。

图3为由不同空间基线长度（即0～200 km）和基线倾角（即0°、±30°、±60°以及±90°）对应的基线误差引起的DEM误差。结果表明，空间基线长度和基线倾角对DEM误差影响显著。对于相同的基线误差而言，空间基线长度越大，DEM误差就越小，反之亦然。另一方面，对于相同的基线误差，基线倾角越大，DEM误差也就越大，反之亦然。这意味着保持较小的基线倾角可以提高GEOSAR DEM估计的准确性。此外，该结果还表明基线误差是GEOSAR DEM生成中的主要误差来源，尤其是对于基线长度较短和基线倾角较大的基线而言。

图2. 斜距误差与GEOSAR DEM绝对误差的关系（视角取名义值4.8°）。

3.3. 基线倾角误差

基于式（1）和式（2），可以得到基线倾角误差δα对GEOSAR DEM估计的影响：

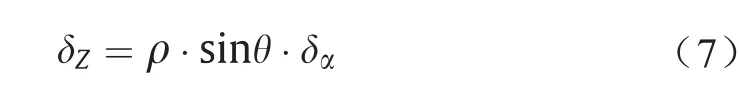
由式（7）可知，基线倾角误差的传播取决于GEOSAR系统的斜距和入射角。图4是由基线倾角误差引起的DEM误差。GEOSAR系统所采用的斜距和入射角如表1所示。由图4可以看出基线倾角误差极大影响了DEM估计的准确性。例如，±0.01°以内（三倍标准差）的GEOSAR基线倾角误差引起的DEM误差最大可达524 m。即使只考虑一个标准偏差的基线倾角（约±0.0033°），DEM的最大误差仍高达173 m。结果表明，基线倾角误差是GEOSAR系统生成DEM的重要误差源。

图3. 在不同空间基线和基线倾角[（a）～（d）分别为0°、±30°、±60°和±90°]条件下，基线误差与GEOSAR DEM绝对误差之间的关系。视角为名义值4.8°。

3.4. 卫星高度误差

根据式（1），可将卫星高度误差δH引起的DEM误差δZ表示为：

考虑到所确定的卫星高度的精度通常在厘米到米级，因此相比于其他误差源，GEOSAR高度误差对DEM估计的影响显得微不足道。

3.5. 相干相位误差

根据式（4），可将干涉相位误差δφ对DEM误差δZ的影响表达为：

图5绘制了由干涉相位误差引起的DEM误差。由图可知，相位误差会严重影响GEOSAR DEM的精度，尤其是在空间基线较短的情况下。例如，相位误差为2时，对于长度为5 km的基线，DEM误差结果约为36 m，而当基线增加至45 km时，DEM误差将减小到4 m左右（图 5）。

4. GEOSAR全球每日DEM产品质量分析

如前文所述，由于卫星重返周期极短，空间覆盖范围巨大，GEOSAR系统具有每日生成全球DEM的潜力。但是，由此生成的DEM质量可能会受到固有误差源的影响，这些固有误差源包括：①前文已分析的误差源；②密集干涉相位条纹；③大气条件的时空变化。

4.1. 固定误差源影响

图4. 基线倾角误差与GEOSAR DEM绝对误差的关系。名义视角为4.8°。

图5. 不同空间基线长度（即5 km、45 km、85 km、125 km和165 km）条件下，干涉相位误差与GOESAR DEM绝对误差的关系，其中，θ =4.8°，α = 0°。

如第3节所述，5个主要的固定误差源（即斜距误差、卫星高度误差、空间基线误差、基线倾角误差和相位误差）会影响GEOSAR系统所生成的DEM精度。这些误差均会影响由GEOSAR或LEO SAR传感器生成的DEM产品质量。但是，由于GEOSAR卫星的飞行高度更高（约36 000 km），这些误差的影响通常会变得更加显著（比利用LEO SAR传感器生成的DEM误差大50倍左右）。因此，如果这些误差不能被适当削弱，则GEOSAR生成的DEM精度可能远低于LEO SAR传感器生成的DEM精度。

目前已有多种方法可以用来提高利用InSAR技术生成的DEM准确性，如使用地面控制点（角反射器）来减少系统误差（如基线和倾角误差[21]），多基线InSAR DEM的重建用于削弱倾斜距离误差[3]，以及为减少噪声提供最大后验估计[22]。这些方法可以潜在地应用于提高GEOSAR DEM的准确性，但仍需要进一步研究来检验这些方法并发掘新的方法。

4.2. 密集干涉相位条纹

如第3节所述，某些误差源（如空间基线误差和相位误差）对GEOSAR DEM的影响与空间基线长度成反比，这意味着通过增加空间基线长度来减少这些误差源的影响是可行的。但是，过长的空间基线会导致干涉条纹更加密集，因为高度模糊度会随着基线长度的增加而降低[1]：

密集的干涉条纹可能会导致相位解缠困难[23]。如果在相位解缠时未能准确恢复出地形相位，则难以获得可靠的地面高程信息。

为说明此问题，图6展示了基于真实DEM [图6（a）]在不同空间基线下模拟出的干涉条纹。高程变化范围为225～2160 m。对于10 km的空间基线，由地形[图6（c）]产生的干涉条纹（未解缠）通常可被成功解缠。但当空间基线增加到50 km或100 km [图6（c）、（d）]时，地形相位条纹将变得过密而难以解缠。

已有一些方法可用来解决这一问题。例如，可以使用外部DEM（如SRTM DEM）来模拟和去除主要的地形相位，然后基于残余的地形相位进行相位解缠[24]。但该方法应用于GEOSAR DEM的生成还需进一步研究。

4.3. 大气时空变化的影响

与LEO SAR传感器的不同在于GEOSAR信号是通过整个大气传播的，而不是仅通过电离层。此外，相比于LEO SAR的集成时间（几秒到几十秒），GEOSAR的集成时间更长（几百秒到几千秒）[25]。大气条件在时间和空间上的变化可能会对InSAR产品造成严重的误差[26,27]。因此，应探究更好的方法削弱大气效应的影响（如文献[28-30]），提高GEOSAR每日DEM产品的精度。

5. 结论

GEOSAR卫星极短的重返周期以及较大的空间覆盖范围使该卫星具有每日生成DEM的潜力。本文分析了此类DEM的潜在质量，并发现由于GEOSAR卫星飞行高度较高，利用GEOSAR系统生成DEM精度可能远低于传统的LEO SAR传感器生成的DEM。因此，应采用恰当的方法来更好地削弱GEOSAR DEM误差源的影响。

图6.（a）DEM；（b）～（d）分别为空间基线10 km、50 km和100 km的未解缠的地形相位。

致谢

本研究得到了香港特别行政区研究资助局（PolyU 152232/17E和PolyU 152164/18E）、香港理工大学可持续城市发展研究院（1-BBWB）的部分支持。

Compliance with ethics guidelines

Zefa Yang, Qingjun Zhang, Xiaoli Ding, and Wu Chen declare that they have no conflict of interest or financial con fl icts to disclose.

Reference

[1] Hanssen RF. Radar interferometry: data interpretation and error analysis.New York: Kluwer Academic Publishers; 2001.

[2] Farr TG, Rosen PA, Caro E, Crippen R, Duren R, Hensley S, et al. The shuttle radar topography mission. Rev Geophys 2007;45(2):RG2004.

[3] Ferretti A, Prati C, Rocca F. Multibaseline InSAR DEM reconstruction: the wavelet approach. IEEE Trans Geosci Remote Sens 1999;37(2):705-15.

[4] Rabus B, Eineder M, Roth A, Bamler R. The shuttle radar topography mission—a new class of digital elevation models acquired by spaceborne radar. ISPRS J Photogramm Remote Sens 2003;57(4):241-62.

[5] Gruber A, Wessel B, Huber M, Roth A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J Photogramm Remote Sens 2012;73:39-49.

[6] Rizzoli P, Martone M, Gonzalez C, Wecklich C, Borla Tridon D, Bräutigam B, et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J Photogramm Remote Sens 2017;132:119-39.

[7] Tomiyasu K, Pacelli JL. Synthetic aperture radar imaging from an inclined geosynchronous orbit. IEEE Trans Geosci Remote Sens 1983;GE-21(3): 324-9.

[8] Tomiyasu K. Synthetic aperture radar in geosynchronous orbit. In:Proceedings of the 1978 Antennas and Propagation Society International Symposium; 1978 Mar 15-19; Washington, DC, USA; 1978.

[9] Guarnieri AM, Tebaldini S, Rocca F, Broquetas A. GEMINI: geosynchronous SAR for earth monitoring by interferometry and imaging. In: Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium;2012 Jul 22-27; Munich, Germany; 2012.

[10] Chao B, Harding D, Cohen S, Luthcke S, Hofton M, Blair JB. Global Earthquake Satellite System requirements derived from a suite of scientific observational and modeling studies. Final Reports. Washington, DC: National Aeronautics and Space Administration; 2002.

[11] Hu C, Li Y, Dong X, Wang R, Cui C. Optimal 3D deformation measuring in inclined geosynchronous orbit SAR differential interferometry. Sci China Inf Sci 2017;60(6):060303.

[12] Zheng W, Hu J, Zhang W, Yang C, Li Z, Zhu J. Potential of geosynchronous SAR interferometric measurements in estimating three-dimensional surface displacements. Sci China Inf Sci 2017;60(6):060304.

[13] Hu C, Li Y, Dong X, Wang R, Cui C, Zhang B. Three-dimensional deformation retrieval in geosynchronous SAR by multiple-aperture interferometry processing: theory and performance analysis. IEEE Trans Geosci Remote Sens 2017;55(11):6150-69.

[14] Kou L, Wang X, Xiang M, Zhu M. Interferometric estimation of threedimensional surface deformation using geosynchronous circular SAR.IEEE Trans Aerosp Electron Syst 2012;48(2):1619-35.

[15] Ruiz-Rodon J, Broquetas A, Makhoul E, Monti Guarnieri A, Rocca F. Nearly zero inclination geosynchronous SAR mission analysis with long integration time for earth observation. IEEE Trans Geosci Remote Sens 2014;52(10):6379-91.

[16] Li D, Rodriguez-Cassola M, Prats-Iraola P, Dong Z, Wu M, Moreira A. Modelling of tropospheric delays in geosynchronous synthetic aperture radar. Sci China Inf Sci 2017;60(6):060307.

[17] Ji Y, Zhang Q, Zhang Y, Dong Z. L-band geosynchronous SAR imaging degradations imposed by ionospheric irregularities. Sci China Inf Sci 2017;60(6):060308.

[18] Zebker HA, Villasenor J. Decorrelation in interferometric radar echoes. IEEE Trans Geosci Remote Sens 1992;30(5):950-9.

[19] Bamler R, Hartl P. Synthetic aperture radar interferometry. Inverse Probl 1998;14(4):R1-R54.

[20] Zebker HA, Goldstein RM. Topographic mapping from interferometric synthetic aperture radar observations. J Geophys Res Solid Earth 1986;91(B5):4993-9.

[21] Rufino G, Moccia A, Esposito S. DEM generation by means of ERS tandem data. IEEE Trans Geosci Remote Sens 1998;36(6):1905-12.

[22] Ferraiuolo G, Pascazio V, Schirinzi G. Maximum a posteriori estimation of height profiles in InSAR imaging. IEEE Geosci Remote Sens Lett 2004;1(2):66-70.

[23] Chen CW, Zebker HA. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J Opt Soc Am A 2001;18(2):338-51.

[24] Zhou C, Ge L, Dong C, Chang H. A case study of using external DEM in InSAR DEM generation. Geo Spat Inf Sci 2005;8(1):14-8.

[25] Long T, Hu C, Ding Z, Dong X, Tian W, Zeng T. Geosynchronous SAR: system and signal processing. Singapore: Springer Nature Singapore Pte Ltd.; 2018.

[26] Ishimaru A, Kuga Y, Liu J, Kim Y, Freeman T. Ionospheric effects on synthetic aperture radar at 100 MHz to 2 GHz. Radio Sci 1999;34(1):257-68.

[27] Sun J, Bi Y, Wang Y, Hong W. High resolution SAR performance limitation by the change of tropospheric refractivity. In: Proceedings of 2011 IEEE CIE International Conference on Radar; 2011 Oct 24-27; Chengdu; 2011.

[28] Hu C, Li Y, Dong X, Wang R, Ao D. Performance analysis of L-band geosynchronous SAR imaging in the presence of ionospheric scintillation.IEEE Trans Geosci Remote Sens 2017;55(1):159-72.

[29] Meyer FJ. Performance requirements for ionospheric correction of lowfrequency SAR data. IEEE Trans Geosci Remote Sens 2011;49(10):3694-702.

[30] Tian Y, Hu C, Dong X, Zeng T, Long T, Lin K, et al. Theoretical analysis and verification of time variation of background ionosphere on geosynchronous SAR imaging. IEEE Geosci Remote Sens Lett 2015;12(4):721-5.