一种融合多特征聚类与神经网络的PM2.5小时浓度预测新模型及其在中国城市的应用

刘辉*，龙治豪，段铸，施惠鹏

Institute of Artificial Intelligence & Robotics (IAIR), Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China

1. 引言

随着发展中国家和地区的工业发展，空气污染问题广受关注。近年来，中国大部分地区出现雾霾天气，空气质量治理已成为国家战略问题。空气动力学直径不超过2.5 μm的颗粒物（PM2.5）含有大量有毒有害物质[1]，是最常见的空气污染物[2]。研究表明，PM2.5污染对呼吸系统和心血管系统有直接影响，与肺癌发病率和死亡率密切相关[3]。PM2.5对天气气候亦有不良影响。例如，PM2.5可能导致异常降雨和加剧温室效应[4-7]。PM2.5浓度预测是缓解PM2.5负面影响的有效方法[8]，对智慧城市大数据的发展也具有重要意义[9]。

1.1. 相关工作

PM2.5浓度预测方法可分为4类：物理模型、统计模型、人工智能模型和混合模型。

物理模型侧重于描述气象和化学因素潜在的复杂排放、传输和转化过程[10]。该方法可以输出准确的预测结果，但是需要大量空气污染物排放信息[11]，且计算成本高[12]。统计模型克服了物理方法的缺点，仅需要简单样本，计算速度快[13]。然而，统计模型仅基于有限样本，没有充分考虑各种影响因素之间的内在关系。单一的人工智能模型能够描述非线性系统的规律，在处理大数据方面有很大优势[14]。其缺点在于神经网络的训练过程具有一定的波动性，难以输出最优结果[15]。

考虑到上述方法的局限性，混合模型在空气污染预测中得到了广泛的应用。混合模型通常包括3个部分：数据预处理、特征选择和预测器。数据预处理可以理清原始数据中复杂的数据关系，提高数据平稳性。特征选择可以改善输入数据结构，降低维数过高导致的模型训练困难。混合模型可以综合各种算法的优点，达到更好的模型性能[16-20]。表1列出了PM2.5浓度预测的前沿研究[16-28]。

表1中列出的PM2.5浓度预测模型很少使用特征选择。如果输入包含PM2.5、PM10、SO2、O3等多个特征，会导致模型训练困难、训练时间增加。复杂的输入数据也会影响模型的鲁棒性[29]，降低模型的精度[30]。目前常用的特征选择算法包括主成分分析（PCA）、相空间重构（PSR）和梯度增强回归树（GBRT）。然而，由于这些方法是基于线性系统假设，因此不适用于空气污染物浓度序列。基于模糊理论的粗糙集属性约简（RSAR）算法具有非线性强、停止准则明确、无需参数等优点[31]。RSAR可以通过不同属性之间的依赖关系获得重要属性集，是热门的特征选择研究方向[32]。聚类算法通常用于数据挖掘和分析[33]。目前存在多种聚类方法，诸如k均值聚类（KC）[34]、可能性c-均值（PCM）[35]、曲线聚类[36]等。与其他算法相比，KC算法具有原理简单、计算速度快、聚类效果好等优点，是目前应用最广泛的聚类算法。将RSAR算法与KC算法相结合，可以利用RSAR为KC算法提供合理的聚类对象，是有价值的研究方向。

表1中的分解算法主要为小波方法，可以将原始数据分解成更平稳的子层。与经验模态分解（EMD）、集成经验模态分解（EEMD）和复数经验模态分解（CEMD）相比，经验小波分解（EWT）算法可以自适应地划分傅里叶谱，选择合适的小波滤波器组[37]。除此之外，可以使用聚类方法进行分解。聚类算法可以根据空气污染工况划分原始数据集，减小样本多样性对模型的影响。然而，尚未有研究将基于时序分解的聚类算法用于PM2.5浓度预测。

表1中的预测器多为物理方法、机器学习和人工神经网络（ANN）。虽然哥白尼大气监测服务（CAMS）、化学天气研究和预报模式（WRFChem）与嵌套空气质量预测模式系统（NAQPMS）具有准确的预测结果，但是这些方法需要大量前期工作与物理化学知识。支持向量机（SVM）、支持向量回归（SVR）和最小二乘支持向量回归（LS-SVR）对参数的选择要求很高，不能处理大数据。传统的神经网络，如反向传播神经网络（BPNN）和进化神经网络（ENN）需要大量的训练，容易过拟合。相比之下，回声状态网络（ESN）具有由重复连接的单元组成的独特的储存器结构，训练简单有效，适用于PM2.5浓度数据等非线性系统[38]。

1.2. 研究创新

综上所述，基于分解的聚类算法、非线性模糊理论算法和ESN算法在PM2.5浓度预测中的研究较少。本研究旨在将这些算法应用于PM2.5浓度预测。本文所提出的混合PM2.5预测模型结合了多特征聚类分解（MCD）、ESN和粒子群优化（PSO）3种方法。在MCD中，首先，采用RSAR算法选择重要的空气污染物变量，利用KC算法对原始PM2.5浓度数据进行聚类，利用EWT算法将聚类结果分解成多个子层。然后，为每个聚类组中的每个分解子层建立一个ESN预测器，利用PSO对ESN模型的初始参数进行优化，完成多步预测计算。最后，综合各子层预测结果，形成最终预测值。实验结果表明该混合模型能够准确预测PM2.5每小时平均浓度。所提出模型的详细信息见本文第2节。

表1 近4年PM2.5浓度预测的主要研究

2. 方法论

2.1. 模型框架

MCD-ESN-PSO混合模型的构建步骤如下。

A部分：MCD

这部分包括RSAR、KC和EWT算法。使用RSAR算法过滤原始空气质量数据，用KC算法对过滤后的属性数据进行聚类，然后利用EWT算法将每个簇的聚类数据分解成多个子层，最后为每个簇中的每个子层建立一个ESN预测器。在该方法中，RSAR算法和KC算法共同实现特征聚类，EWT分解算法将原始时间序列分解成更平稳的子层。RSAR、KC和EWT算法的详细信息分别在第2.2～2.4节中介绍。

B部分：ESN

ESN对分解后的PM2.5浓度数据进行预测。ESN由输入层、储备池和输出层组成。ESN的主要思想是使用储备池模拟一个复杂的动态空间，该空间可以随着输入的变化而改变。根据参考文献[38]，ESN的更新方程和输出状态方程可以用公式（1）和（2）表示：

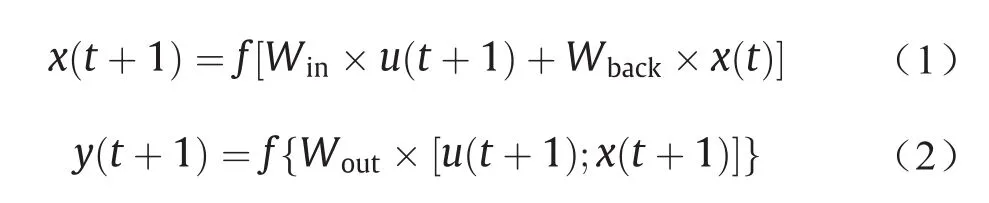
式中，x是从储备池到输出层的输入数据；y是输出；t是时间；u是从输出层到储备层的输出数据；f是ESN函数；Win表示x(t- 1)到x(t)之间的连接权值；u(t + 1)是输出数据；Wback表示输入层到储备池之间的连接权值；Wout表示y(t - 1)到x(t)之间的连接权值。

C部分：PSO

与传统的ESN模型不同，本研究将ESN模型与粒子群算法相结合。在ESN-PSO算法中，通过PSO算法优化ESN模型参数，如输入比例、频谱半径、内部单元数和连通性。

最后，将各子层的预测结果相加，得到最终的预测结果。

2.2. 粗糙属性集约简

RSAR算法可用于剔除冗余信息，同时保持信息质量[31]。在信息系统中，一组对象由一组属性描述[31]。一个知识信息系统的定义如下：

式中，U是对象的有限非空集合；V是非空值的集合；A是属性的有限非空集合；h是将U中对象映射到V中数值的信息函数。

在本文中，A = {PM10, CO, SO2, NO2, O3, PM2.5}是所有属性的集合，V是其数值。f是用于获得γ的依赖函数，γ是集合的依赖关系。

定义一个条件属性集C⊆A和一个属性集P⊆C⊆A，约简应保持排序质量（γ）不变。一个信息表可能有多个约简。所有约简的交集称为决策表的“核心”（core），可表示为core (P)，这是信息系统最重要的属性集。

2.3. k均值聚类

KC是一种简单的迭代聚类算法，使用距离作为相似性指标[34]。它的最终目的是在一组给定的数据集中找到k个簇。KC算法的过程如下：

（1）选择数据空间中的k个对象作为初始聚类中心。

（2）根据样本中的数据对象与聚类中心之间的欧几里得距离，将样本中的数据对象按照最近的中心进行聚类。

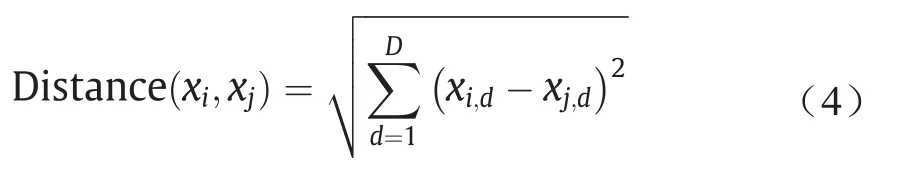
式中，xi是第j个簇中的第i个样本；xj是第j个簇的中心；D表示数据对象的属性数量。

（3）更新聚类中心，即以每个簇中所有对象的均值为聚类中心，计算目标函数的值。

（4）判断聚类中心值与目标函数值是否相等。如果它们相等，则输出结果，否则，返回步骤（2）。

2.4. 经验小波变换

本文采用EWT算法进行数据预处理。EWT由Gilles[37]提出，是一种自适应构造小波的新型信号处理技术。EWT基于小波变换的理论框架，克服了经验模态分解理论的不足和信号混叠的问题。EWT能够自适应地划分傅里叶谱，并选择合适的小波滤波器组。经验尺度函数和经验小波可用公式（5）和（6）表示。

式中，n是分割区间；ω是频率；β是区间[0,1]中满足K阶导数的任何函数；τ是频率系数；β(x) = x4(35-84x+70x2-20x3)；

2.5. 粒子群优化算法

PSO算法由位置z、速度v和自适应函数组成。算法中的每个粒子代表解空间中的一个候选解。根据优化目标设置适应度函数。在计算过程中，每个粒子结合自身和相邻粒子的运动经验更新位置。计算公式[27]如下所示：

式中，m表示迭代次数；vi(m)表示第i个粒子的当前速度；c1和c2表示常数；r1和r2表示0和1之间的随机数；p表示粒子的权重；pibest表示从开始到当前迭代次数的个体最优值；gibest表示从开始到当前迭代次数的组最优值。

3. 实例研究

3.1. 研究地区

我国PM2.5污染物分布范围广泛，主要集中在华北和华中地区[39,40]。为保证实验数据的多样性，应选取PM2.5重污染和PM2.5弱污染等不同场景的数据。在本文中，选择属于华北平原地区的北京、珠江三角洲地区的广州、华中地区的长沙和长江三角洲地区的苏州作为典型城市。选取的样本具有空间代表性，包含不同地理和气候环境下的PM2.5浓度数据，可以很好地验证模型有效性。

空气质量监测站记录了6种空气污染物（PM2.5、PM10、NO2、SO2、O3和CO）的平均浓度。图1展示了选定的数据集及相关介绍。

3.2. 数据描述与划分

实验数据来自北京、广州、长沙和苏州4个城市。Shi等[41]的研究表明地面空间监测的空间有效范围通常为0.5～16 km2，常用值约为3 km2。单个监测站的数据不能代表整个城市的空气质量。为了使样本更具代表性，本文中的数据为每个城市所有空气质量监测站的平均值。这些数据集被命名为D1（北京）、D2（广州）、D3（长沙）和D4（苏州）。将样本数据的长度设置为一年，以覆盖完整的四季。所有实验数据包括2016年1月1日至2016年12月31日采集的PM2.5、PM10、NO2、SO2、O3和CO的每小时平均浓度。所有数据均来自中国国家环境监测中心网站（http://www.cnemc.cn/）。

在数据划分之前，进行缺失值过滤和离群值检查。数据集D1中有220条数据缺失。数据集D2缺少158条数据，数据集D3缺少158条数据，数据集D4缺少157条数据。由于缺失样本数低于总样本集的2.5%，因此直接剔除缺失样本。从图1中可以看出，离群值大多集中在2016年1～3月和10～12月。为了保证模型的训练效果，将离群值视为正常并保留。

剔除缺失样本后，D1有8540个样本，D2有8602个样本，D3有8602个样本，D4有8603个样本。使用数据集的第4001～4600个PM2.5浓度样本训练A组中的模型（没有RSAR-KC的模型，包括ESN、LSTM、ESN-PSO和EWT-ESN-PSO模型）。第4601～5000个样本为测试集，为保证预测效果，遗忘第4601～4900个样本。B组模型（含RSAR-KC的模型，包括RSAR-KC-ESN、MCDLSTM-PSO和RSAR-KC-EWT-ESN-PSO模型）采用RSAR-KC对每个站点的所有实验数据进行预处理。为了保证误差评估的有效性，每个簇被用来训练一个ESN模型，然后对第4901～5000个样本的预测结果进行重构。

为了研究抽样过程对模型精度的影响，采用D1中的第3001～4000个（S1）样本和第6001～7000个（S2）样本进行对比实验。图2显示了数据集S1和S2的分布。

为了进一步验证模型的有效性，实验中使用了D4（包含8603个样本）作为附加数据集。数据集D4从春季、夏季、秋季和冬季选择月度数据进行测试。这些数据被命名为T1（第1000～1999个样本）、T2（第3100～4099个样本）、T3（第5000～5999个样本）和T4（第6000～6999个样本）。它们如图3所示。表2显示了PM2.5浓度数据的相关统计描述。

图1. 空气质量监测站位置。（a）北京。北京是中国的首都，位于华北平原的北端；属典型的暖温带半湿润大陆性季风气候，夏季炎热多雨，冬季寒冷干燥，春季和秋季很短；年平均气温为10～12 ℃，年平均降雨量在600 mm以上。（b）长沙。长沙是长江中游的重要城市；属亚热带季风气候，气候温和、降水充沛、炎热多雨；年平均气温为17.2 ℃，年平均降雨量为1361.6 mm。（c）广州。广州位于中国东南部的珠江三角洲北缘，珠江穿城而过；属热带季风气候，气温高、降雨量大、风速低。（d）苏州。苏州位于江苏省东南部和长江三角洲中部；属亚热带季风型海洋性气候，四季分明，全年雨量充沛。Group A：不含RSAR-KC的模型，包括ESN、LSTM、ESN-PSO和EWT-ESN-PSO模型。

图2. 数据集S1和S2的PM2.5浓度序列。

图3. 数据集T1～T4的PM2.5浓度序列。

表2 PM2.5浓度数据的统计描述

3.3. 结果与讨论

3.3.1. RSAR结果

利用RSAR和KC对原始数据进行预处理。按照国际PM2.5分类系统建立各数据集的属性决策表，对PM2.5浓度数据进行分类离散化。类似地，对其他5种空气污染物的浓度进行离散化。表3为属性约简表。通过计算其他5种大气污染物浓度和PM2.5污染物浓度的正域值，可以确定PM10、NO2、CO、O3和SO2的显著程度分别为0.0825、0.0948、0.0531、0.2189和0.1843。SO2和O3具有重要意义，被判定为已建立的信息决策系统的核心属性。

如果约简属性和决策属性之间的相关性太强，则两者之间没有区别。如果约简属性和决策属性之间的相关性太弱，则它们之间没有相关性。这两种情况下的约简属性都是冗余的。因此，为了保证输入样本的多样性，约简属性的选择需要综合考虑约简属性和决策属性之间的相关性和独立性。本文采用协方差来评价PM2.5浓度与其他污染物浓度的关系，如表4所示。cov (PM2.5,PM10)、cov (PM2.5, NO2)、cov (PM2.5, CO)和cov (PM2.5,SO2)均为正值。cov (PM2.5, O3)为负值。cov (PM2.5,PM10)、cov (PM2.5, NO2)和cov (PM2.5, CO)的绝对值远大于cov (PM2.5, SO2)和cov (PM2.5, O3)的绝对值。在保证输入属性独立性方面，RSAR算法是有效的。为了避免维度灾难给模型训练带来的困难，选择相关程度较高的属性作为核心属性，并将其他相关性较弱的数据作为约简属性。

表3 属性约简表

3.3.2. k均值聚类结果

属性约简后，原始数据集为N× 3的样本空间。使用三维KC算法将该空间划分为多个簇。使用误差平方和（SSE）[42]和轮廓系数（SC）[43]选择k的最佳值。由于3个数据集的聚类结果非常相似，因此以D1为例说明结果。

由图4可见，当选择不同的k时，SSE和SC不同。k值的范围为1～15，SSE值随着k值的增加而减小。当k=3时，SC值最大，此时SSE值也较大。根据图4，综合考虑SSE和SC，选定k值为7。

当k= 7时，原始数据D1被分成7组，结果如图5所示。图5（a）显示了PM2.5的结果，而SO2和O3的结果分别如图5（b）和（c）所示。图5（a）所示的PM2.5的聚类结果是本文的重点部分。聚类簇（C）1的振幅为0～200 μg·m-3，并且波动平缓。C2的振幅为0～55 μg·m-3，短周期波动剧烈。C3的振幅为0～400 μg·m-3，波动平稳，周期性不强。C4的振幅为50～150 μg·m-3，周期性和对称性好。C5的振幅为0～200 μg·m-3，波动比C1更剧烈。C6的振幅为160～240 μg·m-3，波动剧烈，具有很强的对称性。C7的振幅为0～100 μg·m-3，周期明显，但对称性较弱。总体而言，与图1中的原始数据相比，聚类后的数据更加稳定，各簇数据均呈现不同的周期性。

为了得出更有说服力的结论，进一步分析了PM2.5浓度数据的聚类结果的统计描述，结果如表5所示。

7组数据的平均值分别为71.54 μg·m-3、24.00 μg·m-3、285.74 μg·m-3、91.47 μg·m-3、83.90 μg·m-3、177.00 μg·m-3和34.85 μg·m-3。聚类后的7组数据集中，组内数据的波动范围较小。这与图5中每组数据的幅度分布是一致的。

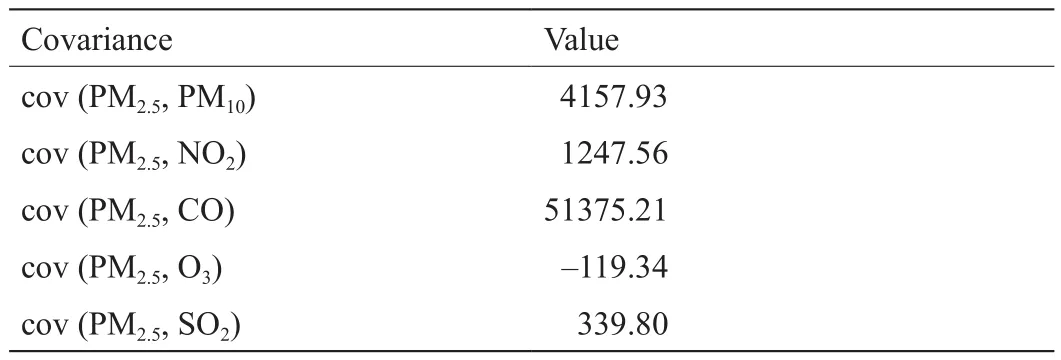
表4 协方差表

标准差反映了群体中个体间的离散度。聚类后的7组数据的标准差值分别为37.02 μg·m-3、14.25 μg·m-3、47.30 μg·m-3、20.96 μg·m-3、32.70 μg·m-3、29.81 μg·m-3、19.42 μg·m-3，均小于聚类前的71.00 μg·m-3。聚类后的各组数据更接近其平均值。如图5所示，每组数据曲线上下波动的对称性较强。

聚类后的7组数据的偏度值分别为0.70、0.72、0.74、0.21、1.01、0.22、0.88，均小于聚类前的2.01。聚类后的数据的波峰对称性更强，即周期规律更加明显。聚类后的7组数据峰度值分别为3.23、2.45、2.50、1.98、4.00、1.82、3.12，均小于聚类前的8.64，减少了聚类后数据在每组数据中的极端分布。在图5中，每组数据波动平稳，没有明显的离群值。

MCD-ESN模型用于分析每个簇中的序列长度。为了保证误差评估的有效性，在每个簇中选取前80%的数据进行模型训练，后20%的数据用于模型预测性能分析。表6展示了每个簇的误差评估指标。

当样本数大于1000时，数据量对预测的影响很小，如C1、C3、C5、C6和C7中的样本数。但是，当样本数小于1000时，模型的预测效果大大降低，这表明ESN网络的预测效果对低样本数（如C2和C4）更为敏感。当聚类后样本数较少时，可以通过增加原序列中的样本数解决。

3.3.3. 预测精度与分析

在本文中，提供了另外6个预测模型作为对比模型，以考察所提出模型的预测性能。此外，为了考察该模型的多步预测性能，所有涉及的模型都进行了一步到三步预测。由于ESN算法的特点，必须遗忘一定数量的输出结果[38]。为了避免预测精度波动，本文对3次重复实验的结果求平均。

本文用平均绝对百分比误差（MAPE）、平均绝对误差（MAE）、均方根误差（RMSE）、误差标准差（SDE）、皮尔逊相关系数（R）和一致性指数（IA）分析预测模型的实验结果。D1、D2和D3模型的指标值如表7所示。从表7可以看出，这3个数据集反映了相同的模型性能。为了使论文的篇幅保持在合理的范围内，只选择D1进行具体分析。图6显示了D1的PM2.5浓度预测结果。表8给出了S1、S2和T1～T4的6个预测模型的R和IA结果。图7给出了S1和S2的6个预测模型的MAPE、MAE、RMSE和SDE结果。图8给出了T1和T2的6个预测模型的MAPE、MAE、RMSE和SDE结果。图9给出了T3和T4的6个预测模型的MAPE、MAE、RMSE和SDE结果。需要注意的是，由于R和IA的值与其他4个评价指标不属于同一维度，所以没有以图表的形式显示。

图4. 不同k值的SSE和SC指标。

图5.（a）PM2.5浓度序列的KC聚类结果；（b）PM2.5和SO2浓度序列的KC聚类结果；（c）PM2.5和O3浓度序列的KC聚类结果。

表5 数据集D1的各簇数据的统计描述

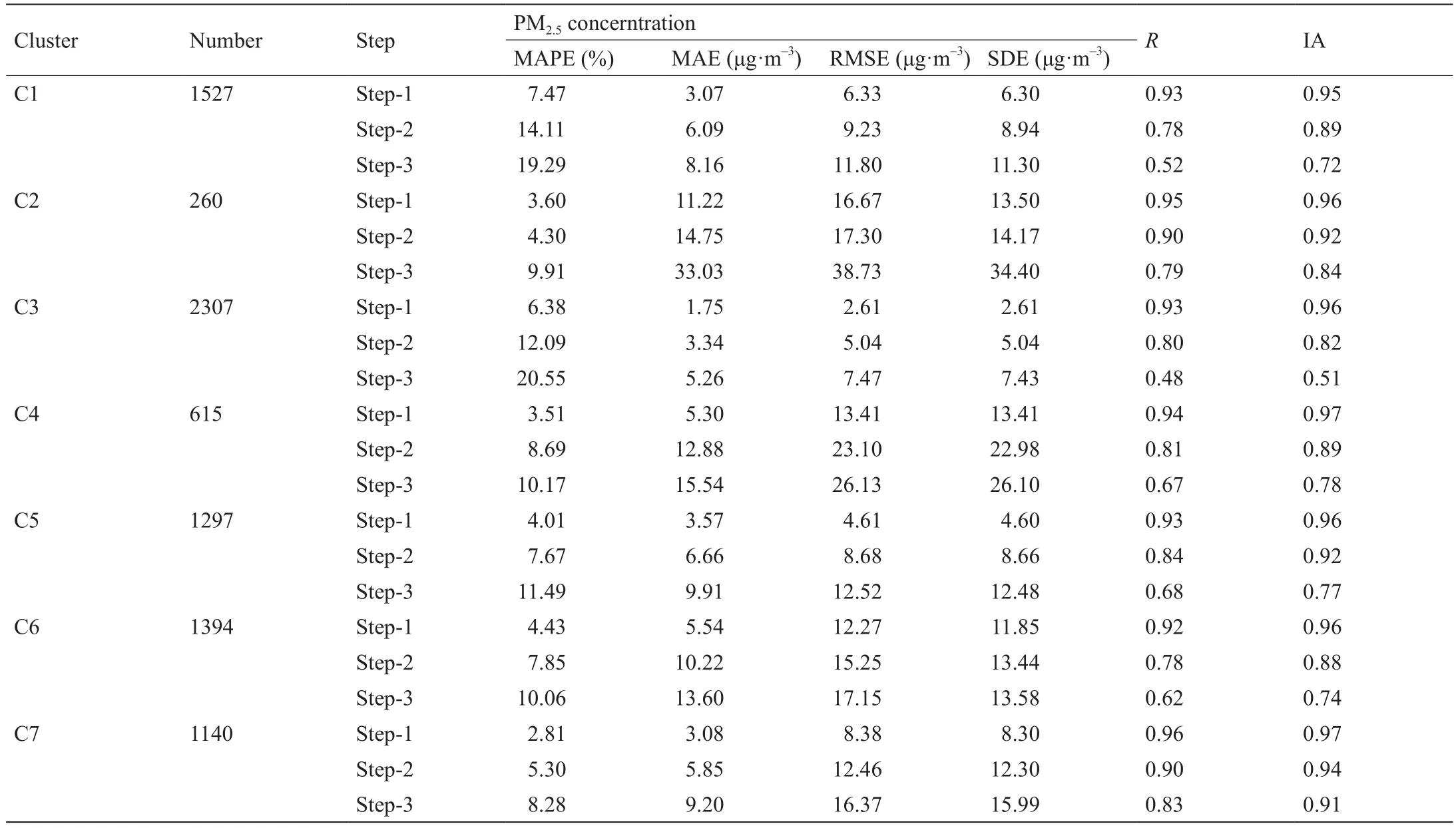
表6 数据集D1各簇PM2.5浓度的MCD-ESN模型预测误差指标

表7 数据集D1、D2和D3的PM2.5浓度预测误差指标

在表7、表8和图6至图9中，本文所提出的模型具有最小的误差评估指标，实现了对PM2.5浓度的准确预测。与其他6种对比模型相比，本文所提出的模型具有更高的多步预测精度，证明了混合模型的有效性。

ESN-PSO模型的预测精度优于ESN模型，说明粒子群算法选择的最优参数有助于提高ESN模型的预测精度。EWT-ESN-PSO模型的预测精度优于ESN-PSO模型，说明加入EWT分解算法可以提高模型的预测精度。EWT算法得到的序列更平稳，随机性更小。因此，将分解后的子层作为模型输入，可以获得更优的预测结果。RSAR-KC-ESN模型的预测精度优于ESN模型，说明RSAR-KC算法可以提高模型的预测精度。聚类后，不同簇之间的差异较大，相同簇之间的相似度较高，可以提高模型的预测精度。

此外，在表7和图6至图9中，每个预测模型的精度都随着步数的增加而降低。随着预测步长的增加，误差累积愈发严重，导致预测精度下降。

空气质量从优开始排序，依次为长沙（D3）、广州（D2）和北京（D1）。表7和图6中的预测精度与此顺序一致。此外，图7中的数据表明，同一地区不同污染水平的样本对模型精度没有影响。S1的PM2.5浓度小于S2，但S2的预测精度高于S1。因此可以得出结论，在空气质量较好的城市，该模型的预测精度要好于污染严重的城市。

图6. 数据集D1的PM2.5浓度超前多步预测结果。

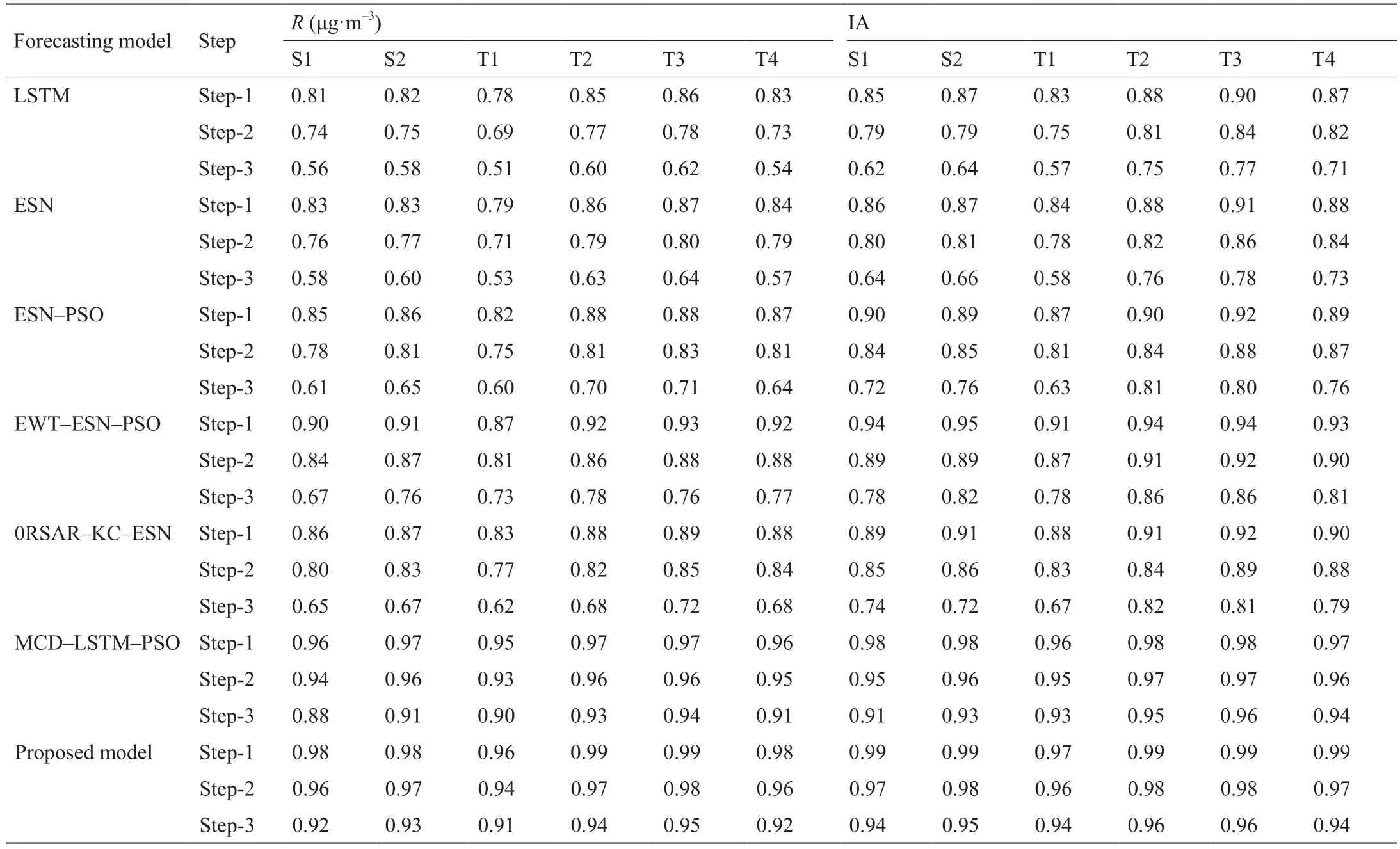
表8 数据集S1、S2和T1～T4的PM2.5浓度预测R值和IA值

图7. 数据集S1（a）和数据集S2（b）的PM2.5浓度预测误差。

在上述分析中，表7和表8以及图6和图7验证了同一时间段内不同城市的数据预测的有效性。为了验证同一城市不同时间段内预测的有效性，进行了图8和图 9所示的实验。根据图8和图9中的数据，本文所提出的模型随着时间段的变化保持了稳定的预测效果，验证了所提出模型在全年的稳定性和有效性。

在本文中，所有的计算均在仿真条件（Intel i5-6500 CPU 3.2 GHz，RAM 8 GB）下进行。表9给出了D1中对比模型的计算时间。由于所提出模型的RSAR-KC算法和PSO算法都是离线处理，因此无法与对比模型比较计算时间。

图8. 数据集T1（a）和数据集T2（b）的PM2.5浓度预测误差。

图9. 数据集T3（a）和数据集T4（b）的PM2.5浓度预测误差。

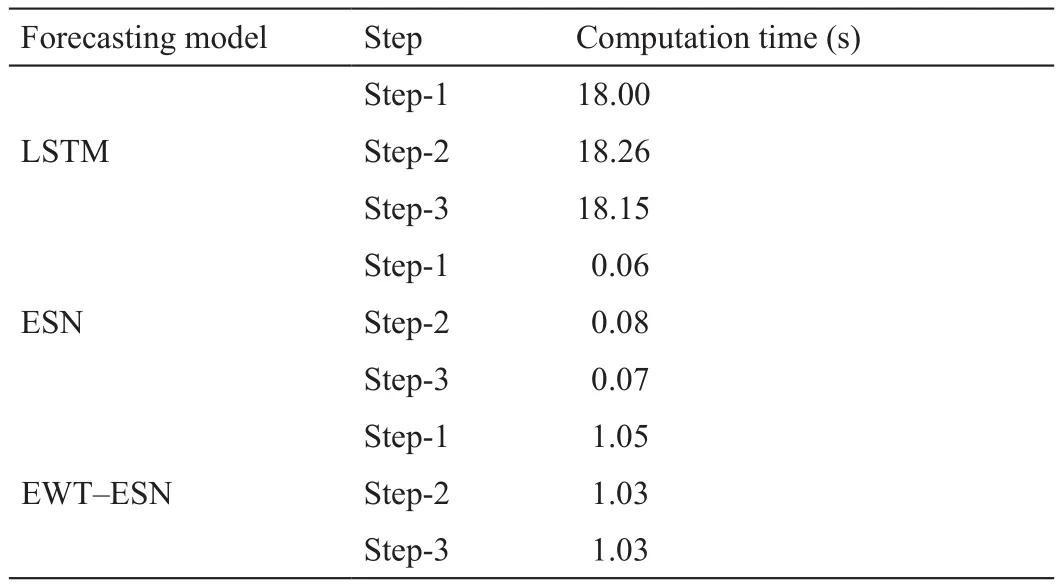
表9 数据集D1的对比模型计算时间

由于ESN网络本身的优势，ESN的计算速度比LSTM快得多。由于储备池的存在，在ESN网络的训练过程中只需要训练输出权值，这大大提高了计算速度。

加入EWT分解算法后，模型的计算速度有一定程度的降低。由于每个分解层都需要训练和预测，所以原始模型的计算速度在这里起着至关重要的作用，这进一步体现了ESN的优越性。

预测步长的改变对模型的计算速度影响不大，这可能是因为算法模型的计算量比较大。

4. 结论

本文基于MCD方法和粒子群算法，建立了改进的混合ESN预测模型，对PM2.5的每小时平均浓度进行了预测和分析。将提出的混合模型与几种基准模型进行了比较，验证了该模型的有效性。属性约简结果表明，SO2和O3浓度在PM2.5浓度预测中起着重要作用。PM2.5浓度数据经过聚类处理后更加平稳，有利于ESN训练。预测结果表明：①MCD方法可以提高模型的精度；②所提出的混合模型比其他深度学习模型或单一模型具有更好的预测精度；③所提出的混合模型在我国4个城市的PM2.5污染物浓度数据上取得了较好的实验结果；④所提出的混合PM2.5预测框架可以应用于其他空气污染时间序列的多步预测。预测结果可以嵌入城市空气污染管理预警系统中。

本文的主要贡献如下：

（1）提出了一种基于MCD、ESN和PSO的PM2.5浓度多步预测模型，该模型对PM2.5每小时平均浓度具有较高的预测精度。多步预测结果可用于PM2.5污染预警系统的开发。

（2）提出了一种新的混合PM2.5浓度预测分解方法，即MCD，该方法将特征提取与分解相结合。利用RSAR算法的特征提取结果进行多维KC聚类，既保证了聚类结果的有效性，又考虑了多维特征的影响。首先采用基于EWT算法的KC算法进行数据预处理。然后根据不同的PM2.5浓度场景，采用聚类算法对原始PM2.5浓度进行分组。最后结合EWT分解算法，对原始PM2.5浓度数据在时间尺度上的不同特征进行判别。

（3）采用ESN作为预测器。ESN模型中神经元的稀疏连接提高了神经网络模型的收敛性，增强了模型的泛化能力，避免了模型训练过程中的过拟合。此外，ESN在计算过程中具有良好的实时性。

致谢

本研究得到国家自然科学基金面上项目（61873283）、长沙市首届杰出创新青年培养计划（KQ1707017）和中南大学2019年度创新驱动计划（2019CX005）的资助。

Compliance with ethics guidelines

Hui Liu, Zhihao Long, Zhu Duan, and Huipeng Shi declare that they have no conflict of interest or financial confl icts to disclose.