采用分而治之策略的快速多标签支持向量机分类算法研究❋
2020-11-04郭忠文孙中卫刘石勇王续澎
刘 竞, 郭忠文, 孙中卫, 刘石勇, 王续澎
(中国海洋大学信息科学与工程学院, 山东 青岛 266100)
与传统分类问题相比,在多标签分类中,每个样本也用单个实例表示,它的不同之处在于,每个实例可以同时拥有多个标签,这样标签之间就不再相互独立[1]。为了解决多标签分类问题,研究者们已经提出了许多多标签分类方法,主要包括采用支持向量机的方法,采用神经网络的方法,采用朴素贝叶斯的方法,采用决策树的方法和采用k最近邻的方法[2]等。这些方法已经在文本分类[3]、图像视频的语义标注[4-5]、生物信息学预测[6]、音乐情感分类[7]等许多领域获得成功运用。但是,在现实世界中存在许多应用,它们需要在大规模数据集上进行多标签分类,这将导致许多原有的多标签分类方法不能被很好地使用。这主要是受到繁重计算复杂度的限制,主要表现为所需训练和测试时间过长,这在支持向量机上尤为明显。本文将聚焦于支持向量机类型的多标签分类技术。
传统的支持向量机(Support Vector Machine,SVM)[8-9]算法只能解决单标签分类问题,经过改进的多标签支持向量机算法[10]可以进行多标签分类。但是,现实世界中的很多应用数据集需要SVM采用非线性核函数,这进一步限制了SVM多标签分类算法在大规模多标签数据集上的使用。
此外,多标签分类算法无法回避的问题是绝大多数的多标签数据集都在遭受一个严重的标签数据不平衡问题[11],这将影响各类算法的分类效果。
本文针对多标签SVM分类算法在大规模数据集上使用所遇到的问题,将结合著名的二元关联问题转换策略和二元DC-SVM[12]分类算法来构建一个新的多标签SVM分类算法(MLDC-SVM)。该算法采用DEC方法来解决标签数据不平衡问题。在二个公共数据集上的实验结果表明:相比于已经存在的基于二元关联问题转换策略的多标签分类算法如ML-LIBSVM[13]、ML-CVM[14]和ML-BVM[15]等,本文的算法在训练和测试时间上是最短的,并且5个评价指标数据显示,本文的算法性能与ML-LIBSVM更接近,且优于ML-CVM和ML-BVM。
1 相关工作
在过去几十年里,由于多标签分类在机器学习、模式识别和统计学等领域受到广泛关注,许多多标签分类算法已经被提出和应用。这些多标签分类方法可以被归纳为下面两个主要策略:问题转换策略和算法改进策略[2]。同时为了解决多标签分类中标签数据不平衡问题,许多标签数据不平衡处理方法被提出和应用并取得良好的效果。本节将按照上面的两个策略介绍一下已有多标签分类方法,介绍一下已经存在的标签数据不平衡处理方法。
问题转换策略主要是把一个多标签分类问题转换为几个单标签分类问题来解决。因此,基于问题转换策略的多标签分类方法主要是通过联合问题转换技巧和已经存在的二元分类方法来实现多标签分类。问题转换技巧主要包括二元关联(Binary relevance)转换技巧、OVO(One-versus-one)转换技巧、OBO(One-by-one)转换技巧和LP(Label powerset)转换技巧[2]等。常用的二元分类方法主要包括SVM、CVM、神经网络、决策树和最近邻等[2]。
在文献[16]中,作者描述了二元关联问题转换策略主要存在的三个问题。首先,由于它假定标签之间是独立的,这将忽略标签之间的关联性和内在依赖性。其次,它将导致标签数据不平衡问题,主要表现为转换后的二元数据集中,负实例数量将远超正实例数量。最后,如果标签的数量过于庞大,标签数据不平衡问题将近一步恶化,同时分类器的数量也将增加。尽管存在这些问题,但二元关联问题转换策略任然是简单实用的并且数据是可逆转的。在文献[17]中,作者着重强调了它的主要优势。首先,它可以使用任何二元分类器作为基础分类器来实现多标签分类。其次,相比于其它的方法,二元关联转换策略有很低的计算复杂度,且计算复杂度与标签的数量呈线性关系。再次,由于标签是独立的,标签的增加或减少将不会影响其它标签分类模型,因此,它可以很容易的并行化。最后,它的最重要的优势是能够优化几个损失函数。基于此,本文将采用著名的二元关联问题转换策略来实现多标签分类。
算法改进策略则通过修改已经存在的分类算法来解决多标签分类问题。Clare和King[18]基于C4.5经典决策树算法提出一个C4.5类型的多标签分类算法,该算法是通过修改信息熵计算公式和允许决策树的叶子节点为一个标签集合来实现多标签分类。该多标签分类算法更适用于小规模数据集。多标签支持向量机(Rank-SVM)被提出在文献[10]中,它是通过扩展多类别支持向量机并且采用最小化排序损失(Ranking Loss)来实现多标签分类,这样做将导致一个极其复杂的二次规划问题。为了克服Rank-SVM算法的训练耗时问题,Xu Jianhua[19-20]采用核向量机(CVM[14])和零标签方法,提出多标签分类算法Rank-CVM和Rank-CVMz,它可以在一定程度上提高训练速度,但将降低分类效果。反向传播多标签分类算法(BP-MLL)[21]引入一个新的误差函数,该函数考虑了多标签分类的特征,使得该算法可以应用于多标签分类,这将导致一个大规模的非约束优化问题。基于k最近邻(kNN)的多标签分类算法ML-kNN[22],它基于待预测样本的k个最近邻样本的类别标签出现的先验和后验概率,使用最大化后验原则确定待预测样本的标签集。该算法只能在小规模数据集上使用。
在文献[23]中详细介绍了标签数据不平衡问题对各种分类算法的影响。为了克服这个问题,已经有许多的对策被提出和使用,并取得良好的效果。这些对策主要可以概括为以下三个主流方法,分别为重采样方法[23]、基于实例的方法[24]和代价敏感方法[25]。本文提出的MLDC-SVM分类算法采用DEC方法来克服标签数据不平衡问题,DEC方法是代价敏感方法的一种具体实现。
尽管许多多标签分类算法已经被提出和应用,但是它们在大规模多标签数据集上的使用将受到一定限制,尤其是基于SVM方法的更为严重。
2 采用分而治之策略的快速多标签支持向量机分类算法(MLDC-SVM)
2.1 二元关联问题转换策略
本文将采用著名的二元关联问题转换策略来实现多标签分类。假定多标签训练数据集S={(x1,Y1),(x2,Y2),…,(xN,YN)},其标签集合为L={1,2,…,k}。二元关联问题转换策略首先把多标签训练数据集S转换为k个独立的二元训练数据子集Sj={(x1,y1),(x2,y2),…,(xN,yN)},j={1,2,…,k}。其中,二元训练数据子集Sj包含多标签训练数据集S的所有实例,但是它的每个实例仅带有一个积极或消极标签,即相应多标签训练实例的标签集合包含标签j,则该实例为积极实例,否者,为消极实例。之后,针对每个标签j使用二元训练数据子集Sj构造相应的二元分类器fj(x)。最后,二元关联问题转换策略构造了一个包含k个二元分类器的集合即HBR,公式如下:
HBR={fj(x)→j′∈{-1,+1}|j∈L}。
(1)
式中,x表示未知的测试实例;j′表示x在fj(x)的预测结果即x是否含有j标签。
为更好的使用二元关联问题转换策略来实现多标签分类,本文将采用下面的决策函数来对每个二元分类数据结果进行集成,从而获取多标签分类结果。该决策函数的公式如下:
Y={j,s.t.fj(x)≥0,j=1,…,k}。
(2)
同时,本文使用以下规则来避免获取一个空的相关标签集合[26],公式如下:
Y={j,s.t.maxfj(x),fj(x)<0,j=1,…,k}。
(3)
从章节1了解到,二元关联问题转换策略是非常实用和高效的。
2.2 采用分而治之策略的二元支持向量机及其改进
假定有一个含有N个数据实例的二元训练数据集,即X={xi:xi∈RD,i=1,2,…,N},它对应的标签集为Y={yi:yi∈[-1,1],i=1,2,…,N}。那么二元支持向量机的原始优化问题可以转化为下面的一个对偶形式的二次规划问题,公式如下:
(4)
公式(4)就是标准的C-SVM模型。在这里参数C是用来平衡模型复杂度和训练样本误差的,α∈RN是对偶变量组成的向量,e∈1N是1组成的向量,αi是α中第i个对偶变量值,Q是一个N×N的矩阵且Qij=yiyj.K(xi,xj),其中K(xi,xj)是核函数。尽管二元支持向量机能够提供一个非常好的分类效果,但是它在大规模数据集上的使用将受到繁重计算复杂度的严重限制。因此,在文献[12]中,作者提出了采用分而治之策略的二元支持向量机分类算法(DC-SVM算法)。为了实现DC-SVM算法,作者首先把全局对偶变量集合分解为w个子集{V1,…,Vw},之后,独立解决各个子分类问题,公式如下:
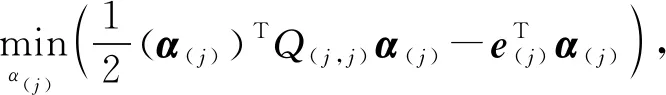
(5)
在这里,j={1,…,w},α(j)代表Vj组成的子向量即{α(j)i|α(j)i∈Vj,i=1,…,|Vj|},Q(j,j)是一个子矩阵且其行数和列数为|Vj|。|Vj|代表了Vj中对偶变量数量,α(j)i是α(j)中第i个对偶变量值,e(j)∈1|Vj|是1组成的向量。

DC-SVM分类算法在标签数据不平衡时,倾向于将实例预测为负实例,其预测结果具有偏斜性。解决该问题的一个有效途径就是在DC-SVM模型中对两类实例选取不同的惩罚参数,对数量较少的正实例选取较大的C值,代表对少类实例的正确识别更为重视,对其错误分类的惩罚也更加严格,这就是DEC方法的基本思想。依据DEC方法,我们将对DC-SVM进行部分改进,以便于它们可以更好的解决标签数据不平衡问题。针对DC-SVM的原始优化问题,我们将其改进为下面的一个对偶形式的二次规划问题,公式如下:
(6)
s.t.0≤α(j)i≤C+,yi=+1,
0≤α(j)i≤C-,yi=-1。
式中C+和C-代表不同惩罚因子。
从公式(6)中可以看出,通过对两类实例选取不同的惩罚参数C+和C-,可以很好地处理不平衡问题。不同的惩罚参数C+和C-的取值将用下面的公式来计算:
C-/C+=n/(pβ)。
(7)
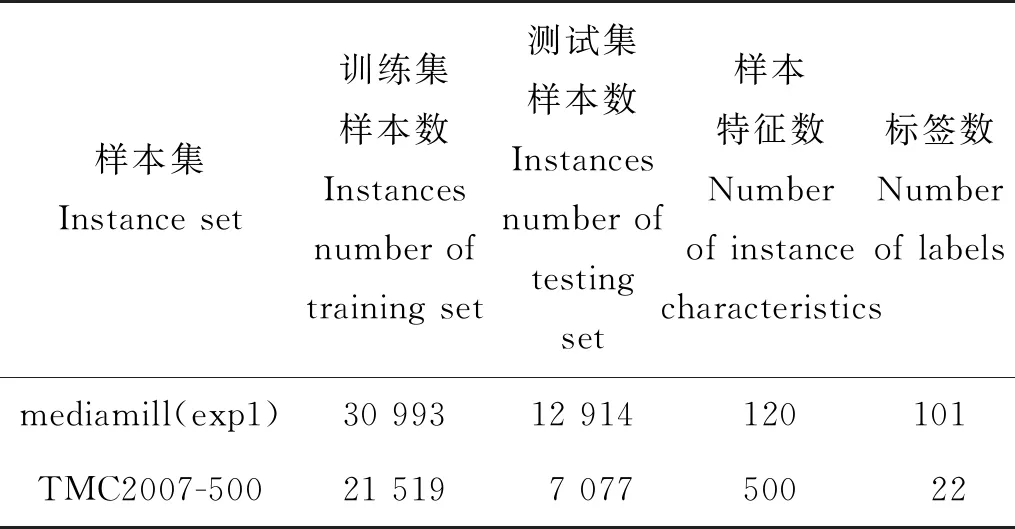
式中:C-/C+代表该训练集的标签不平衡级别;n是训练集的负实例个数;p是训练集的正实例个数;β是一个正整数常量且0<β 本文提出的采用分而治之策略的快速多标签支持向量机分类算法(MLDC-SVM)将采用著名的二元关联问题转换策略来实现多标签分类。首先,把多标签数据集按标签的个数(k)转化为k个二元数据集,其中每个二元数据集是有包含该指定标签的正实例和不包含该指定标签的负实例组成,并且每个二元数据集的实例数目与多标签数据集中的实例数目相同。然后,依据DC-SVM分类算法原理,对DC-SVM分类算法进行改进,使其采用DEC方法来处理标签数据不平衡问题,进而提出IMDC-SVM分类算法来处理每个二元数据集,获取k个二元分类器。最后,通过公式(2)和(3)来集成k个二元分类器的结果,实现快速多标签分类。 IMDC-SVM分类算法首先随机选出m个训练实例;其次采用Kernel Kmeans算法对选出的实例进行聚类;获取w个聚类中心;然后依据聚类中心把训练数据集分解为w个训练数据子集;然后,针对每个训练数据子集获取标签数据不平衡程度,并采用LIBSVM算法来进行训练,使用LIBSVM算法主要是因为它很好地实现了DEC方法和SMO算法;最后通过集成每个训练数据子集的解决方案来获取全局训练数据集解决方案。算法1和2分别给出了IMDC-SVM算法和MLDC-SVM算法的伪代码。 算法1. IMDC-SVM算法 输入:S-二元训练数据集 {(x1,y1),(x2,y2),…,(xN,yN)}。 w-数据聚类中心个数, β-正实数常量。 BEGIN (1) 从二元训练数据集S中随机取样m个实例即 {(x1,y1),(x2,y2),…,(xm,ym)}。 (2) 在{(x1,y1),(x2,y2),…,(xm,ym)}上运行Kernel Kmeans算法获取w个聚类中心即c1,…,cw。 (3) 对于二元训练数据集S,依据聚类中心c1,…,cw,划分为w个二元训练数据子集即V1,…,Vw。 (4) FOR每个二元训练数据子集Vc,(c=1,…,w) DO (a)计算消极实例数量nc; (b)计算积极实例数量pc; END END 算法2. MLDC-SVM算法 输入:S-多标签训练集 {(x1,Y1),(x2,Y2),…,(xN,YN)}。 x-测试实例(x∈X), k-标签数量, β-正实数常量, w-数据聚类中心个数。 输出:Y-测试实例的预测标签集合 (Y∈Y)。 BEGIN (1) 对于多标签训练集 S={(x1,Y1),(x2,Y2),…,(xN,YN)}, 使用二元关联问题转换策略分解多标签训练集S为k组独立的二元训练数据集即S1,S2,…,Sk。 (2) FOR每个二元训练数据集 Sj,(j=1,2,…,k) DO 使用公式(6),训练采用非线性核的IMDC-SVM分类器 fj=IMDC-SVM(Sj,w,β)。 END FOR (3) 获取测试实例x的预测标签集合 IF (所有fj(x)<0) Y={j,maxfj(x)},(j=1,2,…,k), 使用公式(3) ELSE Y={j|fj(x)≥0},(j=1,2,…,k), 使用公式(2)。 END IF END 在算法2中,Sj表示第j个二元训练数据集,fj表示使用Sj训练获得的第j个标签的预测模型,fj(x)表示测试实例x在第j个标签预测模型中的预测值。 由于公式(6)中有N/w个对偶变量,在实际中IMDC-SVM的时间复杂度至少为 O(N2/w),空间复杂度为O(N2/w2)。 MLDC-SVM算法的时间复杂度至少为O(kN2/w),空间复杂度为O(kN2/w2),其中k表示标签的数量,w表示数据聚类中心个数,N表示数据集实例数量。 本文将选取三种已经存在的多标签分类算法即ML-LIBSVM、ML-CVM和ML-BVM来与我们提出的MLDC-SVM分类算法进行比较。它们都将采用二元关联问题转换策略将多标签分类问题转换为多个二元分类问题来处理。但是它们的不同之处体现在对转换后的二元分类问题的处理方法上。ML-LIBSVM将采用LIBSVM方法[13]来解决二元分类问题,ML-CVM将采用CVM方法[14]来解决二元分类问题,ML-BVM将采用BVM方法[15]来解决二元分类问题。这三种方法都通过整合所有二元分类问题的结果来获取多标签分类结果。 实验选用了两组公共的大规模多标签数据集,这些数据集可以在网站https://www.csie.ntu.edu.tw/cjlin/libsvmtools/datasets/和http://computer.njnu.edu.cn/Lab/LABIC/LABIC_Software.html[27]上下载。其数据集的规模及属性见表1。 表1 实验数据集特征Table 1 Characteristics of experimental data sets 与单标签分类系统相比,多标签分类系统的评价准则要更加复杂[1,28-29]。本文将选择当前流行的5个评价指标作为评判标准,它们分别是:汉明损失(Hamming loss)、1-错误率(One-error)、覆盖率(Coverage)、排序损失(Ranking loss)和平均精度(Average-precision)。 在这5个评价指标中,平均精度的值越大,说明多标签分类算法的分类效果越好,其它4个的值越小,说明多标签分类算法的分类效果越好。 针对数据集TMC2007-500,为了获取最优解决方案,相应参数设置为w=10,4个多标签分类算法的参数e和C的设置分别为e=9.5e-5,C=1.0。表2和3给出了4种不同的多标签分类算法在该数据集上的实验结果。 表2 在TMC2007-500数据集上的实验结果Table 2 Experimental results on TMC2007-500 data set 表3 在TMC2007-500数据集上花费的时间Table 3 Time spent on TMC2007-500 data set /s 表2中的数据表明MLDC-SVM分类算法与ML-LIBSVM分类算法相比,在Coverage、Ranking loss、Hamming loss和One-error上的值分别上升0.052 9、0.29%、1.4%和1.22%,在Average-precision上的值下降1.82%。这充分说明了MLDC-SVM分类算法的分类效果与ML-LIBSVM分类算法相近,并且要大大优于ML-CVM分类算法和ML-BVM分类算法。同时,从表3中可以看出,MLDC-SVM分类算法在训练和测试时间上是最短的,分别是ML-LIBSVM算法的1/5.33和1/10.02,是ML-CVM算法的1/2.03和1/9.26,是ML-BVM算法的1/1.24和1/5.80。 针对数据集mediamill(exp1),为了获取最优解决方案,相应参数设置为w=10,4个多标签分类算法的参数e和C的设置分别为e=1.95e-5,C=1.0。表4和5给出了4种不同的多标签分类算法在该数据集上的实验结果。 表4中的数据表明MLDC-SVM分类算法与ML-LIBSVM分类算法相比,在Ranking loss、Hamming loss和One-error上的值分别上升0.63%、2.42%和19.92%,在Coverage和Average-precision上的值分别下降4.352和15.83%。这充分说明MLDC-SVM分类算法的分类效果与ML-LIBSVM分类算法相近,且在Hamming loss、One-error和Average-precision等指标上要大大优于ML-CVM分类算法和ML-BVM分类算法。同时,从表5中可以看出,MLDC-SVM分类算法在训练和测试时间上是最短的,分别是ML-LIBSVM算法的1/4.73和1/8.39,是ML-CVM算法的1/3.64和1/20.39,是ML-BVM算法的1/1.39和1/9.24。 综上所述,在两组大规模多标签数据集上的实验结果表明,本文提出的MLDC-SVM分类算法在常用的5个评价指标上的分类效果相近于ML-LIBSVM分类算法,且优于ML-CVM和ML-BVM分类算法。它极大的降低了算法的训练和测试时间,同时也能适应标签数据不平衡情况。这些将极大的提高MLDC-SVM分类算法在大规模多标签数据集上的适用性。 表4 在mediamll(exp1)数据集上的实验结果Table 4 Experimental results on mediamll(exp1) data set 表5 在mediamill(exp1)数据集上花费的时间Table 5 Time spent on mediamill(exp1) data set /s 本文针对使用非线性核的SVM多标签分类算法在大规模多标签数据集上的使用将受到繁重计算复杂度严重限制的问题,提出了采用分而治之策略的快速多标签支持向量机分类算法(MLDC-SVM)。它通过采用DEC方法能够更好地处理标签数据不平衡问题。这些都将极大地提高该算法在大规模多标签数据集上的适用性。在两组公共的大规模多标签数据集上的实验结果表明,MLDC-SVM分类算法在极大提高训练和测试速度的同时能够取得与ML-LIBSVM分类算法相近的分类性能,并且优于ML-CVM和ML-BVM分类算法的分类性能。未来的工作是改进该算法,使其能够利用标签的相关性信息来提高分类性能。2.3 采用分而治之策略的快速多标签支持向量机分类算法
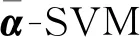
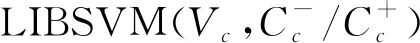
2.4 时空复杂度分析
3 实验验证
3.1 三种已经存在的多标签分类方法
3.2 多标签数据集和评价指标
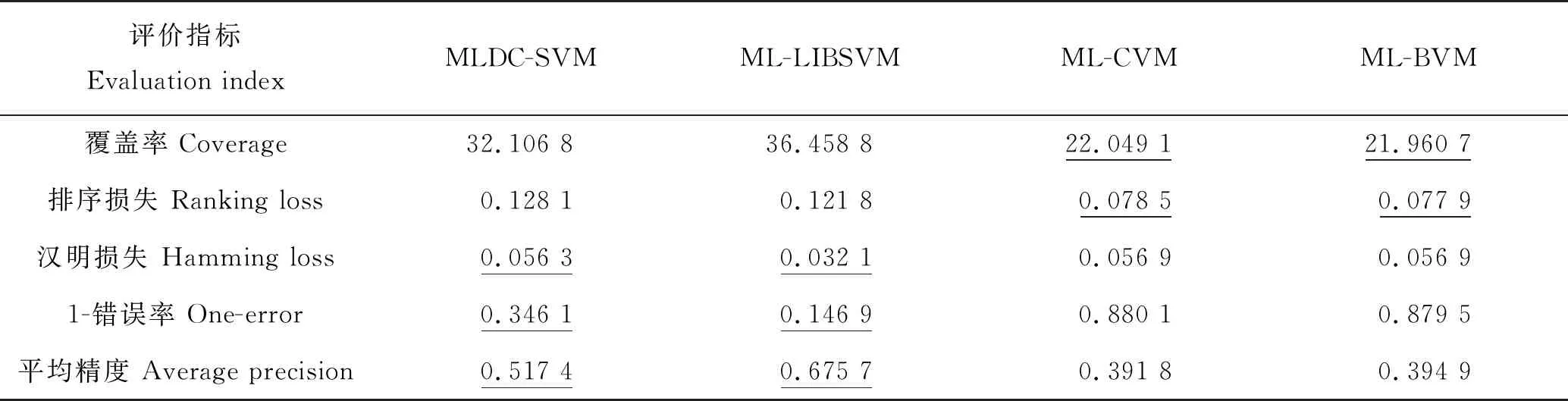
3.3 实验设置与结果分析
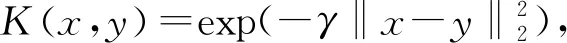



4 结语
