孤立波作用下植物带消浪特性对比分析❋

龚尚鹏， 陈 杰,2,3❋❋， 蒋昌波,2,4， 何 飞， 陈克伦

(1. 长沙理工大学水利工程学院； 2. 洞庭湖水环境治理与生态修复湖南省重点实验室；3. 水沙科学与水灾害防治湖南省重点实验室；4. 湖南省环境保护河湖疏浚污染控制工程技术中心, 湖南 长沙 410114)

海啸是威胁沿海地区安全的海洋灾害之一[1]。2004年印度洋海啸后，沿海植物带在海啸防灾减灾方面成为热门话题[2]。海啸与植物的相互作用属近岸植物水动力问题，前人针对植物与规则波和不规则波开展了大量研究。正弦波和不规则波常用于模拟由海面大气引起的风浪[3]。与震荡波相比，海啸波波长较长、传播速度较快，其引起的水质点运动不限于浅层水体，海啸波这类推进波作用下的植物水动力特性呈现显著差异。

在众多沿海植物带类型中，红树林和海滩林是低纬度的海岸防护工程中较为常见的植物带[4]。海岸红树林广泛分布在全球120多个国家和地区[5]，主要物种包括红树属、木榄属和海桑属等，其特征是枝干茂密，根系发达，根部能起到良好的消浪作用。研究表明，红树林可对海啸波起到显著的削弱作用[6-8]。现实情况下，海滩林也是一种分布较广，能有效抵御海啸等极端气候危害的海岸植物。与红树林相比，海滩林根部埋藏在土壤中，无消浪效果。海滩林主要包括松树、木麻黄、椰子树、桐棉和露兜树等。2004年印度洋海啸和2011年日本海啸的现场调研均发现海滩林能有效减少海啸灾害[9-10]。

值得注意的是，红树林和海滩林作为两类主要的海岸防护树种，将它们统一研究，对比分析有利于完善植物消浪的体系。目前，在近岸植物与海啸相互作用的研究工作中，学者对分别对红树林包含红树[11]、海桑树[12-13]、木榄[11,14]、秋茄[13]等和海滩林包括露兜树[9]、松树[10,15]和木麻黄[9,16-17]等进行了研究，得到了红树林和海滩林的消浪特性。但现阶段尚未有研究来对比分析这两类植物消浪特性的差异。

综上所述，本文拟设计两种不同的物理模型来概化模拟海岸红树林和海滩林，对比分析两类植物的消浪特性，为采用近岸植物消波护岸提供一定的依据。

1 理论分析

孤立波的传播特性和波形与海啸波相近，众多波浪水槽实验研究中，用孤立波来近似模拟海啸波[1,6,8]。波高H的孤立波，在水深h的水中传播，波面方程η(静水面至波面距离)的一阶解为：

η=Hsech2[k(x-ct)]。

(1)

其中：波速c和波数k分别为：

(2)

(3)

孤立波波能与水深和波高相关，孤立波的波能表达式为：

(4)

式中：Es为孤立波波能；ρ为水的密度；g为重力加速度。

入射波波高为Hi的孤立波传播过植物带，其波浪能量可分为三部分：一部分能量透过植物以透射波的形式传播；另一部分能量被植物带阻挡而形成反射波；剩余的能量由于波浪与植物带以及边界相互作用造成的水体紊动和摩擦生热而耗散。由波浪能量平衡方程得：

Et+Er+Edis=Ei。

(5)

两边同时除以Ei可得到：

(6)

式中：Ei、Et、Er、Edis分别为入射波波能、透射波波能、反射波波能和衰减波能。

(7)

式中：Ht、Hr、Hdis分别为透射波波高、反射波波高和衰减波高。

定义透射系数、反射系数和衰减系数分别为：

(8)

将式(8)代入式(7)则有：

(9)

透射系数Kt越小，反射系数Kr越大，衰减系数Kdis越大，表示植物对孤立波传播变形的影响越大。

同时，本文植物带淹没度α定义如下：

(10)

式中：hv为植物高度。

参考何飞等[18]植物分布密度的定义，本文植物分布密度计算公式如下：

(11)

式中：ψ为单位面积植物分布密度；N为分布区域内的植物总株数；Si为单株植物树干横截面面积；S为分布区域面积。

2 实验概述

实验在长沙理工大学水沙科学与水灾害防治湖南省重点实验室的波浪水槽内进行。波浪水槽长宽高分别为40.0、0.5和0.8 m。水槽一端配有推板式造波机，另一端配有消浪网。根据《波浪实验规程》，植物带布置在距离造波板18.2 m处，植物带前布置两个浪高仪G1和G2用于入射波高采集并分离反射波高，植物带内部1/3和2/3处分别布置浪高仪G3和G4用来采集植物带内部沿程波高，植物带后端0.5 m处布置透射波高采集仪G5。圆形表示单株植物。实验布置如图1所示。

图1 实验布置图Fig.1 Experimental setup

本文红树林研究对象为成熟红树群落(见图2(a))，在蒋昌波[19]的模型设计基础上，结合Mazda[12]和Lee[20]对红树的调查资料，同时参考白玉川[21]和Husrin[22]研究，同时考虑到实验条件的限制，红树林模型设置长度为1.5 m，每列布置4株，植物前后间距为13.6 cm。考虑到红树林的根须数量、根须直径等复杂的几何因素，对树根部分仅做概化模型(见图2(b))，模型采用的几何比尺为1∶10。采用硬质塑料球架模拟植物根部，塑料球架的杨氏模量E为(2±0.5) GPa，塑料球架由一大一小两种尺寸组成，能较好的模拟红树林根部复杂程度，根部外圈直径wr为8.0 cm，高度hr为5.0 cm。假定树干刚性且无弯曲和折断，采用直径wt为1.0 cm的圆柱模拟红树林模型树干，PVC圆柱的杨氏模量E为(35.3±3.9) GPa，在孤立波作用下不会发生形变，符合要求。树冠部分枝杈较多，树叶宽大，选取具有一定柔性的聚乙烯材料模拟红树林冠部。聚乙烯的杨氏模量E为(1.2±0.1)GPa。冠部直径wc为10.0 cm，冠部高度hc为20.0 cm。

本文海滩林研究对象为成熟木麻黄(见图2(c))，参考Tanaka[23]和刘宪钊[24]对木麻黄的研究，木麻黄分布宽度较宽，实验模型设置长度为2 m。每列布置4株，植物前后间距为12.3 cm。考虑到海滩林的根埋藏在土壤中，模型仅包含树干和树冠两部分(见图2(d))。海滩林的树干部分采用有机玻璃管，有机玻璃杨氏模量E为(15.9±13.5) GPa，直径wt为1.0 cm。海滩林树冠部分多有较多枝杈，叶面狭窄。应当指出的植物冠部的消浪实质是枝杈以及枝叶对波浪水体所产生的紊动耗散，为了实现对其冠部进行量化研究，采用30根外径为0.6 cm的有机玻璃管对植物冠部进行模拟，冠部外围直径wc为9.0 cm，冠部高度hc为20.0 cm。

图2 红树林和海滩林Fig.2 Mangroves forests and beach forests

孤立波波高H，水深h可以确定孤立波水动力特性，值得注意的事，由于实际情况中两类植物带分布密度差异，本实验设置了不同的植物带长度和分布密度。因此，参考Mei等[25]研究，定义无量纲长度kL，本文红树林无量纲长度范围为0.96≤kL≤3.12，海滩林无量纲长度范围为0.99≤kL≤4.16。无量纲长度kL综合反映了实验波浪波长和植物带长度的影响。考虑无量纲长度范围相近时的植物带消浪特性对比分析。

如表1所示，红树林进行12组实验工况研究，包含4种水深，每种水深3种入射波高。海滩林进行16组实验工况研究，包含4种水深，每种水深4种入射波高。实验首先在波浪水槽内安置植物带模型和浪高仪，调整水槽内水位至实验水位，随后开启造波机并且预热30 min，保证造波机造波性能稳定，再开启数据采集仪。待水面平稳后开始造波，并测量波高数据。完成一组实验后，等待水面平稳，再进行下一组次实验。

表1 实验工况Table 1 Research cases

3 结果与分析

3.1 波面变化

图3给出了由G2和G5号浪高仪采集的测量入射波、反射波和透射波的示例，入射波高H为9.0 cm。可以看出，孤立波入射波(G2)波形良好，由于水槽内水体体积恒定导致波面尾端(5.5～9.0 s)低于静水面，传播至植物带时，不同位置的植物阻挡孤立波传播，产生较紊乱的反射波(9.0～13.0 s)。传播透过植物带后，透射波(G5)的波形仍为孤立波，但波高有明显衰减，表明植物带有良好的消浪效果。

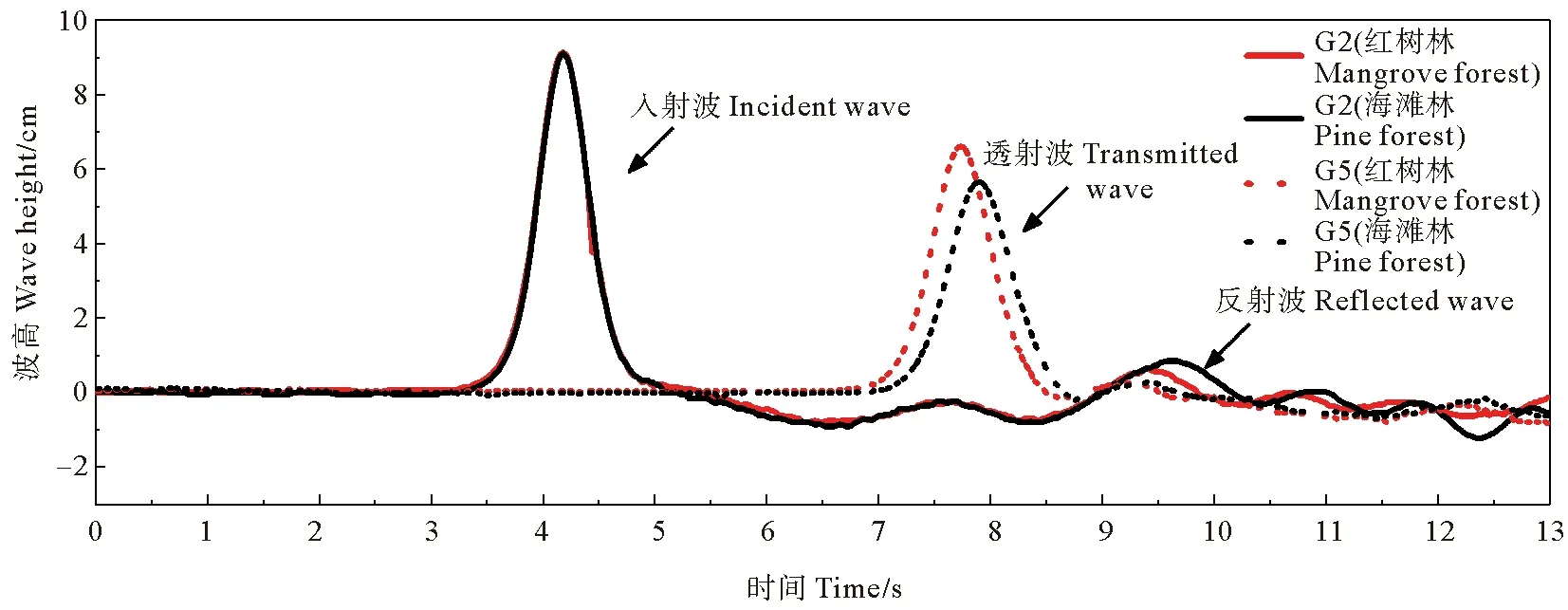
图3 植物带自由液面时间序列Fig.3 Time series of surface evelation in the vegetation belt

3.2 波高对植物带消浪特性的影响

在4种淹没度α情况下，两种模型的透射系数Kt和耗散系数Kdis随波高H变化的对比实验结果如图4所示。结果显示，在淹没度α=0.56、0.67和0.78时，两种模型透射系数Kt均随波高H增大而减小，耗散系数Kdis均随波高H增大而增大。且在淹没度α=0.56、0.67时，随着波高H的增大，两种模型消浪效果的差异缩小。在淹没度α=0.78和1时，两种模型消浪效果差异随波高H增大而增大。如图4(d)所示，在淹没度α=1时，两种模型表现出不同的消浪特性，海滩林模型消浪效果随波高增大而增强，而波高对红树林模型的消浪效果影响较小，植被消浪特性的差异性可能是由两类植物模型的冠部结构与材料刚性差异性导致。

3.3 淹没度对植物带消浪特性的影响

两种波高H情况下，红树林模型和海滩林模型的透射系数Kt和耗散系数Kdis随淹没度α变化的实验结果如图5所示。结果显示，两种模型随淹没度的变化规律基本相同，不同的波高情况下呈现出不同的消浪特性。如图5(a)所示，当H=5.0 cm且0.56≤α≤0.67时，淹没度对植物带消浪效果影响较大，淹没度越高，消浪效果越好。此后，淹没度对植物带消浪效果影响较小，随着淹没度越大，两种植物带消浪效果趋于相同。如图5(b)所示，当H=9.0 cm时，植物带消浪效果先随淹没度增大而增强，在α=0.78时消浪效果达到最好，此后消浪效果反而随淹没度增大而减弱。综上所述，植物带消浪特性与淹没度相关，两种类型的植物带消浪特性基本相同，淹没度在0.78附近植物带消浪效果较好。

3.4 无量纲水深对植物带消浪特性的影响

图6(a)分别给出了不同植物模型情况下模型的透射系数Kt、耗散系数Kdis和反射系数Kr随无量纲水深kh的实验结果。无量纲水深kh反映了水动力因素对植物带消浪特性的影响。结果表明，红树林模型与海滩林模型的消浪特性随无量纲水深kh变化规律和变化速率基本相同。Kt均随kh增大而减小，Kdis均随kh增大而增大。kh对Kr影响不大。

3.5 无量纲长度对植物带消浪特性的影响

图6(b)分别给出了不同植物模型情况下模型的透射系数Kt、耗散系数Kdis和反射系数Kr随植物带无量纲长度kL的实验结果。结果显示，红树林模型与海滩林模型的消浪特性随无量纲长度kL变化规律基本相同。透射系数Kt均随无量纲长度增大而减小，红树林模型的透射系数Kt变化速率较松树模型的透射系数Kt变化速率大。耗散系数Kdis均随无量纲长度增大而增大，红树林模型的耗散系数Kdis变化速率较松树模型的透射系数Kdis变化速率大。无量纲长度对反射系数Kr影响不大，但两种模型反射系数差距明显。分析原因为两种模型的冠部弹性模型E存在较大差异，海滩林模型弹性模型E较大，导致海滩林的反射系数较大。同时由于孤立波绝大部分波浪能量都集中在波峰附近，因此，海滩林模型反射系数较红树林反射系数大。

(图中红色代表红树林模型结果，黑色代表海滩林模型结果，方形代表透射系数，圆形代表耗散系数。Red represents the mangrove model results, black represents the pine forest model results, square represents the transmission coefficient, and circle represents the dissipation coefficient.)

(图中红色代表红树林模型结果，黑色代表海滩林模型结果，方形代表透射系数，圆形代表耗散系数。Red represents the mangrove model results, black represents the pine forest model results, square represents the transmission coefficient, and circle represents the dissipation coefficient.)

(图中红色代表红树林模型结果，黑色代表海滩林模型结果，方形代表透射系数，圆形代表耗散系数，三角形代表反射系数。Red represents mangrove forest model results, black represents pine forest model results, square represents transmission coefficient, circle represents the dissipation coefficient, triangle represents reflection coefficient.)

4 结语

通过物理模型实验研究了红树林和海滩林两种典型植物带的消浪特性。实验结果表明波高H、淹没度α、无量纲水深kh和无量纲长度kL均在不同程度上影响植物消浪特性。两种类型的植物带消浪特性随淹没度、无量纲水深和无量纲长度的变化规律基本相同，波高对消浪特性的影响仅在当淹没度等于1时，波高变化对红树林模型消浪特性基本无影响，而海滩林消浪效果随波高增大而增大。在本实验条件下得到了海啸波在两种典型的植物带的传播特性，揭示了植物带消浪特性与波高、淹没度、无量纲水深和无量纲长度的内在联系，得到了海啸波作用下两种典型植物带消浪特性的异同，为海岸工程种植植物带护岸提供了一定的参考。