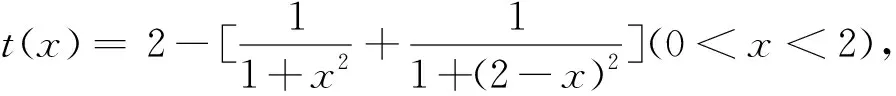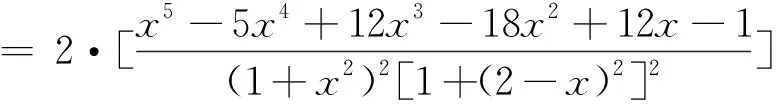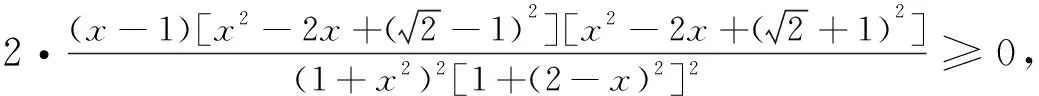从两个三角征解题的解看三角问题代数思维

贵州省毕节市七星关东辰实验学校 (551700) 刘先海 魏 星

文[1]指出，三角问题都是方程x2+y2=1下的二元函数t=G(x,y)的值域问题，即未知数符号化(x=cosθ,y=sinθ)的方程函数问题(文[2])，因此，代数(特殊二元二次方程x2+y2=1)，几何(单位圆x2+y2=1)，三角(x=cosθ,y=sinθ)是统一的，把复杂的三角问题化为代数问题，用基本的方程与函数思维，自然且简单.

例1 在锐角ΔABC中，已知b2cosAcosC=4accos2B，求y=sin2BcosB的最大值(数学通讯(学生版)，2019第10期，问题420).

分析：y=sin2BcosB=cosB(1-cos2B)是关于cosB的一元函数，故只需在b2cosAcosB=4accos2B中求cosB的取值范围.

解:由正弦定理b2cosAcosC=4accos2B⟺sin2BcosAcosC=4sinAsinCcos2B⟺

例2 已知ΔABC中，sinC=2cosAcosB，求sin2A+sin2B的最大值和最小值(数学通讯,2019年第11期,问题征解422).

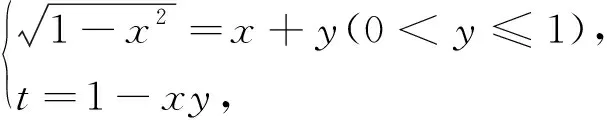
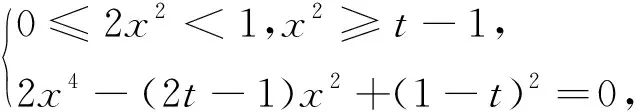
解法2：由sinC=2cosAcosB>0得A,B都是锐角，sinC=2cosAcosB⟺sin(A+B)=2cosAcosB

⟺sinAcosB+cosAsinB=2cosAcosB⟺tanA+tanB